考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制方法

崔惟 曹逸凡 李程昊 張紫薇 劉明洋 張皓 顏偉

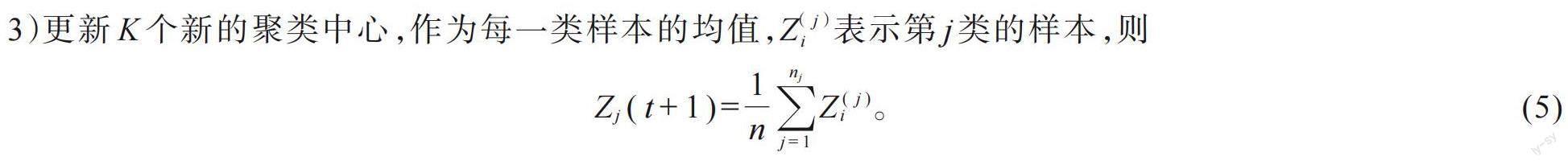
doi：?10.11835/j.issn.1000-582X.2022.203

收稿日期：2021-10-15

網(wǎng)絡出版日期：2022-02-16

基金項目：國網(wǎng)河南省電力公司科技項目資助（52170220009X）。

Foundation：Supported by Science and Technology Project of State Grid Henan Province Electric Power Company （52170220009X）.

作者簡介：崔惟（1986—），男，高級工程師，博士，主要從事電力系統(tǒng)優(yōu)化運行與控制研究，（E-mail）cuiwei_sgcc@163.com。

通信作者：顏偉，男，教授，博士生導師，（E-mail）cquyanwei@cqu.edu.cn。

摘要：為了應對風電隨機波動導致的送端電網(wǎng)潮流大規(guī)模變化、換流母線電壓擾動，進一步導致?lián)Q流站離散設備額外動作，提出考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制方法：首先通過定義功率相對偏差來描述風電波動程度，篩選出二級電壓控制中不能忽略風電功率波動的特征時段；然后采用k-means聚類方法得到特征時段風電出力的典型場景；最后利用概率場景法來表示風電的隨機性，借助機會約束法解決不確定性優(yōu)化問題。基于修改的IEEE39節(jié)點算例系統(tǒng)進行仿真并驗證所提方法的有效性。

關鍵詞：電力系統(tǒng)；協(xié)調(diào)二級電壓控制；風電接入；交直流系統(tǒng)；不確定性優(yōu)化

中圖分類號：TM712 ?????????文獻標志碼：A ?????文章編號：1000-582X（2023）09-041-11

Coordinated secondary voltage control method of AC/DC system considering wind power randomness

CUI Wei¹， CAO Yifan²， LI Chenghao¹， ZHANG Ziwei²， LIU Mingyang¹， ZHANG Hao¹， YAN Wei²

（1. Electric Power Scientific Research Institute of State Grid Henan Province Electric Power Company，Zhengzhou 450052，P. R. China; 2. State Key Laboratory of Power Transmission Equipment &System Security and New Technology， Chongqing University， Chongqing 400044， P. R. China）

Abstract： To address the challenges posed by large-scale changes of the sending grid tide and the voltage disturbance in converter buses caused by random fluctuation of wind power， which further leads to additional actions of the discrete equipment in the converter station， this paper proposes a coordinated secondary voltage control method for AC-DC systems that consider the randomness of wind power. Firstly， the degree of wind power fluctuation is quantified by defining the relative deviation of power， and characteristic time periods of wind power fluctuation which cannot be ignored in the secondary voltage control are identified. Next， the k-means clustering method is employed to obtain typical scenarios of wind power output during these characteristic time periods. Finally， the probabilistic scenario method is used to represent the randomness of wind power， and the uncertainty optimization problem is solved using the chance constraint method. The effectiveness of the proposed method is validated through simulations conducted on a modified IEEE39 node arithmetic system.

Keywords： power systems; coordinated secondary voltage control; wind power fluctuation; AC-DC system; uncertainty optimization

隨著電力系統(tǒng)電壓無功控制技術的日益發(fā)展，分級電壓控制已經(jīng)成為中國各省級電網(wǎng)調(diào)控中心能量管理系統(tǒng)的核心功能^[1?4]。二級電壓控制處于分級電壓控制的中間層，有著不可或缺的地位。在當前中國風電大規(guī)模通過直流線路遠距離傳輸電力的背景下，將存在一些風電功率短時波動較大的時間段，二級電壓控制中計算周期內(nèi)潮流分布不變的假設不再成立，導致現(xiàn)有確定性交直流協(xié)調(diào)二級電壓控制^[5?7]的效果在風電大規(guī)模集中接入的前提下難以保證，因此有必要研究考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制。

由于風電功率隨機性、間歇性的波動，大規(guī)模風電的集中接入極大地增加了電力系統(tǒng)電壓無功控制的難度和復雜度^[8?9]，因此需要分析風電功率隨機波動性，為二級電壓控制決策是否考慮風電隨機性提供參考。風力發(fā)電功率是一個隨機變量，可以用全場景來模擬其隨機性。為了滿足計算效率的要求，需要對場景進行壓縮減小計算規(guī)模。在場景模擬方面，Shi等^[10]用場景對風機的隨機出力進行描述，建立了含多臺風機的發(fā)電調(diào)度優(yōu)化模型。王玲玲等^[11]利用概率場景法描述風電功率的隨機性和負荷功率的隨機擾動，建立考慮不同風機之間時空相關性的配網(wǎng)無功優(yōu)化模型。在場景壓縮方面，k-means聚類是一種常用的場景壓縮方法，實現(xiàn)起來簡單方便。明杰等^[12]用k-means聚類方法對風電原始數(shù)據(jù)進行聚類，并通過聚類指標確定最優(yōu)聚類數(shù)。Fang等^[13]提出一種基于k-means聚類的對于初始點要求過強的風電場分類方法。

文中從直流近區(qū)協(xié)調(diào)二級電壓控制的角度出發(fā)，用某實際風電場的全年以1 min為采樣周期的數(shù)據(jù)作為全場景^[14]來表示風電波動的隨機性，通過k-means聚類方法^[12，15]對場景進行壓縮，按照距離代價函數(shù)指定場景聚類數(shù)，將特征時段的場景壓縮成多個典型場景，實現(xiàn)對風電功率波動的場景模擬。對于所篩選出的特征時段，在考慮換流站離散設備動作要求的協(xié)調(diào)二級電壓控制模型^[5]基礎上，提出了考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制模型，借助機會約束規(guī)劃法^[16?18]對不確定性優(yōu)化問題進行求解。

1風電功率隨機波動特性分析及其場景模擬方法

1.1風電功率隨機波動特性分析

文中以某風電場群A的2019年全年以1 min為采樣周期的風電有功功率數(shù)據(jù)為基礎，來分析研究風電功率的波動特性。該風電場群的總風機數(shù)為552臺，裝機容量為752.4 MW，通過220 kV匯集站并入電網(wǎng)。

風電功率呈現(xiàn)顯著的隨機波動特性，風電場群A的全年功率曲線如圖1所示。由圖可知，年大部分時間內(nèi)日均出力都是小于額定出力，少部分時間達到額定出力，風電出力介入零與裝機容量之間隨機波動。日間的風電出力同樣波動很大，最小出力接近于零，最大出力接近于550 MW，不利于電力系統(tǒng)的安全穩(wěn)定運行。從季節(jié)尺度看，冬春季出力相對較大，在12月時達到最大值，在夏秋季出力相對較低，在8月達到最小值，這是由本地冬春季季風較強、夏季季風較弱的風速季節(jié)分布特點決定的。

由圖2可知，風電場群功率變化一階差分量概率密度曲線為窄高型、概率分布集中、離散程度小、功率波動小；單機功率變化一階差分量概率密度曲線為寬矮型、概率分布寬、離散程度大、功率波動大。整體上按單機、風電場、風電場群規(guī)模化方向風電出力波動性依次減弱，表現(xiàn)出“平滑效應”，即區(qū)域總體波動性減弱的空間互補效應。

綜上所述，從風電出力在不同時間尺度下的波動規(guī)律、日內(nèi)特性和季節(jié)差異等方面分析風電的波動時間效應，從單機、風電場和風電場群3個角度分析風電波動特性與風電功率的空間相關性，如表1所示。

1.2風電功率波動的特征時段選取

確定性交直流系統(tǒng)協(xié)調(diào)二級電壓控制^[5]建立在隨機源荷功率在控制周期內(nèi)保持不變的假設之上，當隨機源荷在控制周期內(nèi)波動很小時，該控制策略基本能夠滿足重要節(jié)點電壓的控制要求和節(jié)點電壓的安全約束。然而，當隨機源荷在控制周期內(nèi)波動過大時，不僅會導致重要節(jié)點電壓偏離期望值過大，影響換流站近區(qū)電壓質(zhì)量，增加換流站離散設備額外投切風險，而且會影響換流站近區(qū)無功潮流在已有控制策略下分布不均，發(fā)電機發(fā)出無功不均衡等問題。因此，文中定義控制周期內(nèi)有功功率相對偏差來描述風電的波動特性，描述風電功率波動程度，具體表達式為

其中，

式中：t₀為控制周期初始時刻；t為控制周期，t取值為15 min；P為風電功率，可以表示成當前時刻的風電功率測量值與隨機功率偏差之和；△P為風電功率在控制周期內(nèi)的波動值功率；ρ%為功率相對偏差。特別地，控制周期初始時刻的偏差為零。

文中認為當控制周期內(nèi)的風電功率波動會引起變電站電壓無功控制設備的電容器投切動作則為大幅波動，反之則認為是小幅波動。因此，在協(xié)調(diào)二級電壓控制周期內(nèi)，以調(diào)節(jié)發(fā)電機無功出力為主要手段，盡可能快速、連續(xù)平衡源荷功率的大幅波動，避免換流站離散設備額外投切動作，減小電壓無功控制成本。風電大幅波動的界定條件為

式中：ΔQ為風電無功功率偏差；D為補償電容器的死區(qū)系數(shù)；Q_c為一組電容器容量。

將全年有功無功數(shù)據(jù)按季節(jié)和時段來進行劃分，根據(jù)經(jīng)驗認為一個時段內(nèi)有20%以上的時刻其風電波動為大幅波動，就將其界定為特征時段篩選出來。并認為在特征時段內(nèi)的協(xié)調(diào)二級電壓控制需要考慮風電的隨機性，而其他時段的協(xié)調(diào)二級電壓控制則不需要考慮風電的隨機性。

1.3基于k-means聚類的風電功率場景壓縮方法

風電原始場景規(guī)模較大，會在隨機優(yōu)化中出現(xiàn)計算速度較慢的問題。為了提高計算效率，可將原始場景壓縮成少量具有代表性的典型場景來替代大規(guī)模原始場景。文中采用在傳統(tǒng)風電場景聚類中應用較多的k-means聚類方法，將歐式距離作為評價指標，聚類后的K個聚類中心點即為保留場景，具體步驟如下。

1）設樣本容量為N，每個樣本的觀測指標為M，需要聚類的數(shù)據(jù)為Z_N×M，指定聚類數(shù)目k。初始時刻t=1，選擇k個樣本作為初始凝聚點Z_j（t）（j=1，2，…，K）。

2）計算每個樣本到初始聚類中心的歐式距離D（Z_i，Z_j）（i=1，2，…，N），找到最小的歐式距離，則樣本Z_i屬于C_m類。遍歷每個樣本，對所有樣本完成一次聚類，每一類中有n_j個樣本。最小的歐式距離為：

4）若聚類中心不再變化，即Z_j（t +1）=Z_j（t）時，則聚類過程結束，否則返回步驟2）。

設第i個典型場景包含的樣本數(shù)為N_i個，則該典型場景概率為

通過式（6），可依次計算出各典型場景的概率。典型場景反映初始樣本整體的隨機狀態(tài)，其概率之和為1。在k-means聚類法中，聚類后的場景數(shù)應事先設定，而場景數(shù)如何選擇的關鍵是建立聚類有效性指標進行評價。文中引入距離代價函數(shù)^[19]作為評價最佳聚類數(shù)有效性的指標，表達式為

式中：F為距離代價函數(shù)，為類際距離和類內(nèi)距離之和；L為類際距離，為所有聚類中心到空間中心的距離；D為類內(nèi)距離，為每個簇內(nèi)部的樣本到其聚類中心的距離的總和；m為所有樣本的平均值，m_i為簇C_i所含樣本的平均值；k為聚類數(shù)；p為空間內(nèi)任一樣本。

不同的聚類數(shù)導致距離代價函數(shù)有不同，距離代價函數(shù)F越小，聚類效果越好。通常情況下，最佳聚類數(shù)K≤。

2考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制模型

對于風電波動較大的特征時段，風電功率的隨機波動對換流站近區(qū)電壓無功的影響不可忽略，因此筆者在文獻[5]的基礎上引入風電功率波動的隨機性，建立考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制模型。假設給定無功分區(qū)中，有n_p個中樞點，n_g個受控發(fā)電廠節(jié)點，n_w個風電節(jié)點，n_d個送端換流站，下標s來表示場景變量，s=1，2，…，N，所建控制模型以下詳細介紹。

2.1目標函數(shù)

考慮中樞點電壓偏差和發(fā)電機無功均衡度的目標函數(shù)為

目標函數(shù)中包含2項：第一項為中樞點與換流母線節(jié)點電壓偏差最小目標，表示所有中樞點與換流母線節(jié)點的電壓當前值與其參考值之差的平方和盡可能小；第二項為發(fā)電機無功出力均衡度目標，表示分區(qū)內(nèi)所有發(fā)電機無功出力比例的平方和盡可能小。假設中樞點電壓偏差最小目標的優(yōu)先級高于發(fā)電機無功出力均衡目標，即目標權重W_a大于W_q，目標函數(shù)為雙目標的場景期望最小。

2.2約束條件

模型考慮的約束條件包括發(fā)電機的控制能力約束、換流器的控制能力約束、中樞點電壓安全約束和換流站關口無功約束。在采用機會約束規(guī)劃法處理隨機約束時，考慮到發(fā)電廠高壓側母線電壓約束為決策變量約束，發(fā)電機的無功出力約束和發(fā)電廠高壓母線電壓的單步調(diào)整量約束為剛性的物理約束，換流器觸發(fā)角約束和換流站關口無功約束是為了使換流變壓器分接頭和無功補償設備不動作，要求這些約束必須100%滿足，而發(fā)電機機端電壓控制變量約束和其余的潮流不等式約束則允許有一定的概率可不滿足。基于上述約束處理思路，以下為所建模型約束方程的具體表示。

1）?發(fā)電廠高壓側母線電壓單步調(diào)整量約束為

2）?發(fā)電廠高壓側母線電壓上下限約束

3）?中樞母線電壓上下限約束

4）?發(fā)電機無功出力上下限約束

5）?發(fā)電機機端電壓上下限約束

6）?換流器觸發(fā)角上下限約束

7）?換流關口無功上下限約束

由式（10）—（17）可知，文中所建立的考慮風電隨機性交直流系統(tǒng)協(xié)調(diào)二級電壓控制模型的目標函數(shù)為二次函數(shù)，約束方程為線性函數(shù)，是一個不確定性二次規(guī)劃問題。文中通過Matlab軟件平臺quadprog函數(shù)的調(diào)用對其進行求解。

3算例仿真

3.1風電場景處理

3.1.1 風電特征時段選取

文中所選取的風電場群A的220 kV匯集站，配備的電容器一組容量為8 Mvar，假定電容器的死區(qū)為80%，則換算到電容器動作的功率偏差ΔQ為6.4 Mvar。對風電場群A典型日的有功無功數(shù)據(jù)進行統(tǒng)計分析，可以擬合得到式（18）所示函數(shù)。其中，擬合參數(shù)分別為：和方差為337.8，確定系數(shù)為0.996，均方根為0.435 4。

通過前文提出風電功率波動的特征時段篩選方法，遍歷原始數(shù)據(jù)，篩選出符合條件的春季12：00—19：00的7個時段作為特征時段，其功率偏差概率密度曲線如圖3所示。

圖3中，7個特征時段功率偏差概率密度曲線對稱分布，在[-10，10]區(qū)間分布較為集中。7個特征時段功率最大偏差分別為44.44、37.39、42.61、53.44、56.17、64.85、126.01 MW，遠高于夏季、秋季、冬季偏差值。

3.1.2 基于k-means聚類的場景壓縮

文中在進行場景壓縮時增加和風電場群A處于一個縣地理位置相近的風電場群B，認為其特征時段和A相同。2個風電場均接入220 kV的匯集站，風電場群A裝機容量為752.4 MW，風電場群B裝機容量為1 233 MW。2個風電場群A和B的數(shù)據(jù)均為2019年以每1 min為采樣間隔的風電功率實測數(shù)據(jù)，不存在相關性問題。現(xiàn)對2個風電場群一個特征時段春季17：00—18：00以1 min為采樣周期的數(shù)據(jù)進行場景壓縮。基于風電功率數(shù)據(jù)，生成不同k值下的距離代價函數(shù)曲線，如圖4所示。

由圖4可知，距離代價函數(shù)整體上先快速下降后在[0.5，1]區(qū)間內(nèi)振蕩，當聚類數(shù)K=20時，距離代價函數(shù)最小，因此對于這一特征時段的風電場景，聚類數(shù)選為20。

在Matlab R2014軟件下，基于k-means聚類方法，對風電功率偏差數(shù)據(jù)進行場景壓縮，可以得到壓縮后的場景及其概率如表2所示。此時壓縮后的20個風電典型場景，其類內(nèi)距離為1 292.5，類際距離為528.6。

3.2考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制仿真

3.2.1 基礎數(shù)據(jù)

以修改的IEEE39節(jié)點算例系統(tǒng)為基礎，在發(fā)電節(jié)點31和32旁增加節(jié)點40和41，模擬發(fā)電廠高壓側母線，修改的IEEE39節(jié)點系統(tǒng)分區(qū)和中樞點信息如表3所示。接線圖及分區(qū)方案^[20]如圖5所示。基于異步電網(wǎng)的背景，在4號節(jié)點處接入送端直流換流站，直流線路與遠端異步電網(wǎng)相連。送端換流站采用定功率、定換流變壓器變比控制，受端換流站采用定電壓、定熄弧角控制。送端換流站的直流功率為1.086 p.u.（基準功率為1 000 MW），受端換流站通過控制直流電壓使送端直流電壓維持在0.92 p.u.（基準電壓為5 00 kV）。換流變壓器的當前變比為1.09，調(diào)節(jié)范圍為1±15×0.01。換流變壓器等值電抗為0.1 Ω，換相效應系數(shù)為0.995。在換流站內(nèi)有并聯(lián)電容器作為無功補償裝置，一組額定容量為80 Mvar，組數(shù)是6組。換流器觸發(fā)角的范圍是8°～18°。

系統(tǒng)劃分為4個無功分區(qū)，圖中紅圈所示為中樞點，藍圈所示為換流母線節(jié)點，加入發(fā)電廠高壓側母線后新增的4條支路參數(shù)見表4所示。

風電并網(wǎng)點為節(jié)點5和14，5節(jié)點接入風電場群A，14節(jié)點接入風電場群B。風電節(jié)點5和14的初始有功功率分別為5 MW和8 MW，初始無功功率分別為10 Mvar和6 Mvar。以風電場群A和B春季17：00—18：00時段的數(shù)據(jù)為樣本，風電場群A和B的裝機容量分別為752.4 MW和1 233 MW，通過統(tǒng)計可以得到20個基于風電初始功率的功率偏差典型場景及其概率如表1所示。風電接入點均在2號無功分區(qū)，中樞點7的電壓對風電節(jié)點有功功率靈敏度為5.10×10^-4和1.21×10^-3，中樞點7的電壓對風電節(jié)點無功功率靈敏度為1.01×10^-2和1.27×10^-2，中樞點電壓對風電節(jié)點無功功率靈敏度為對風電節(jié)點有功功率靈敏度的10倍以上，因此文中提出的協(xié)調(diào)二級電壓控制模型可以忽略風電有功功率波動對節(jié)點電壓的影響。

對2號無功分區(qū)進行協(xié)調(diào)二級電壓控制的仿真，其他分區(qū)的發(fā)電機和負荷參數(shù)保持不變。節(jié)點電壓安全范圍設置為：中樞點電壓為0.95～1.05 p.u.，發(fā)電機機端電壓和發(fā)電廠高壓側母線電壓為0.9～1.1 p.u.，發(fā)電機機端電壓單步最大調(diào)整量為0.01 p.u.。設定中樞點電壓約束和發(fā)電機機端電壓約束的置信水平為90%。

3.2.2 仿真方案

為驗證文中所提方法的有效性，在網(wǎng)絡參數(shù)和運行條件皆相同的條件下，對2號無功分區(qū)采用以下2種控制方案。

方案1：不考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制。

方案2：文中提出的協(xié)調(diào)二級電壓控制。

3.2.3 仿真結果與分析

表5給出了2種方案的發(fā)電廠高壓側母線電壓控制策略，表中ΔV_h40和ΔV_h41分別為發(fā)電廠高壓側母線節(jié)點40和節(jié)點41的電壓調(diào)節(jié)量。將其應用到所有風電場景中，得到2種方案下的控制效果，如表6所示。

從交流系統(tǒng)指標來看，在考慮了風電隨機性后，方案2的中樞點電壓偏差平均值為0.017 6，比方案1降低了0.011 3，下降幅度為39.10%。方案2的換流站母線電壓偏差平均值為0.011 8，比方案1降低了0.002 5，下降幅度為17.48%。方案1的無功均衡因子為1.411 0，方案2的無功均衡因子為1.403 2，較方案1降低了0.007 8，下降幅度為0.56%，表明方案2中發(fā)電機的無功出力更均衡。這說明了文中提出的考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制能夠適應控制周期內(nèi)各種可能的風電出力，在全場景下能夠降低中樞點和換流站節(jié)點的電壓偏差，提高電壓質(zhì)量，提高發(fā)電機無功出力均衡度，有利于交直流系統(tǒng)的穩(wěn)定運行。

從直流系統(tǒng)指標來看，方案2的換流站吸收無功比方案1略降低了0.011；方案1的換流器觸發(fā)角的越限次數(shù)為32次，而方案2的越限次數(shù)減少到0次。這是因為換流器觸發(fā)角約束和換流站無功關口約束是必須完全滿足的約束，使得換流變壓器分接頭以及無功補償裝置減少不必要的動作。相應地，為了增加控制的彈性，發(fā)電機控制變量約束與網(wǎng)絡約束則允許在一定的概率下不必全部滿足。文中提出的模型計及了風電功率波動對換流器觸發(fā)角的影響，充分調(diào)動交流側發(fā)電機的電壓無功調(diào)節(jié)能力，大幅減少由于交流側隨機擾動導致的換流器觸發(fā)角越限，降低換流變壓器分接頭動作次數(shù)。

綜上分析，在風電大幅波動下，考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制方法能夠進一步保證多風電接入的交直流系統(tǒng)的電壓質(zhì)量，降低中樞節(jié)點與換流站母線的電壓偏差，提高發(fā)電機無功均衡度，減少直流設備動作次數(shù)，整體控制效果突出。

4結論

風電的隨機性一直是新能源發(fā)電有待攻克的難點之一，文中通過對風電場群進行功率特性分析，針對風電波動較大的場景，提出了考慮風電隨機性的交直流系統(tǒng)協(xié)調(diào)二級電壓控制方法，明確了發(fā)電廠高壓母線的決策變量性質(zhì)以及發(fā)電機機端電壓的隨機控制變量性質(zhì)，采用概率場景法將風電隨機功率偏差表示成典型場景，通過機會約束規(guī)劃法解決不確定性優(yōu)化問題。文中所提出的方法有如下特點：

1）考慮了風電功率波動的隨機性，并用隨機功率偏差來表示，采用概率場景法來描述這種隨機性，表示為風電無功功率偏差的多個典型場景；

2）明確了公共的決策變量和隨機的控制變量，考慮到二級電壓控制對一級電壓控制的決策問題，選取發(fā)電機機端電壓作為隨機控制變量，發(fā)電廠高壓側母線電壓這一狀態(tài)變量作為決策變量，在所有場景下控制變量不同，而決策變量保持不變；

3）采用機會約束規(guī)劃法處理隨機的目標函數(shù)和約束，要求目標函數(shù)的期望最小并使?jié)M足節(jié)點電壓安全約束的概率大于一個置信水平；

4）本模型在風電波動較大的時段優(yōu)勢明顯，能夠適應風電未來一段時間內(nèi)各種可能的出力情況，顯著減小中樞點電壓偏差，降低了中樞點和發(fā)電機機端電壓的越限風險，具有重要的工程價值。

參考文獻

［1］??孫宏斌， 郭慶來， 張伯明， 等. 面向網(wǎng)省級電網(wǎng)的自動電壓控制模式[J]. 電網(wǎng)技術， 2006（S2）： 13-18.

Sun H B， Guo Q L， Zhang B M， et al. Automatic voltage control scheme for large-scale power networks[J]. Power System Technology， 2006（S2）： 13-18.（in Chinese）

［2］??張明曄， 郭慶來， 孫宏斌， 等. 應用于北美電網(wǎng)的自動電壓控制系統(tǒng)設計與實現(xiàn)[J]. 電網(wǎng)技術， 2013， 37（2）： 349-355.

Zhang M Y， Guo Q L， Sun H B， et al. Design and implementation of automatic voltage control system applied to a power grid in northeast US[J]. Power System Technology， 2013， 37（2）： 349-355.（in Chinese）

［3］??Duan J J， Shi D， Diao R S， et al. Deep-reinforcement-learning-based autonomous voltage control for power grid operations[J]. IEEE Transactions on Power Systems， 2020， 35（1）： 814-817.

［4］??Yuan K L， Lin S J， Liu M B， et al. Analysis of steady state voltage stability in large scale power grid including actions of CSVC[C]//2012 Asia-Pacific Power and Energy Engineering Conference. IEEE， 2012： 1-5.

［5］??顏偉， 胡顯文， 崔惟， 等. 考慮LCC-HDVC設備額外動作要求的協(xié)調(diào)二級電壓控制方法[J]. 電網(wǎng)技術， 2022， 46（4）：1511-1518.

Yan W， Hu X W， Cui W， et al. Coordinated secondary voltage control method considering additional action requirements of LCC-HDVC equipment [J]. Power System Technology， 2022， 46（4）：1511-1518. （in Chinese）

［6］??Xu F D， Guo Q L， Sun H B， et al. A secondary voltage control method for an AC/DC coupled transmission system based on model predictive control[C]//2015 IEEE Power & Energy Society General Meeting. IEEE， 2015： 1-5.

［7］??陳江瀾， 張蓓， 蘭強， 等. 特高壓交直流混合電網(wǎng)協(xié)調(diào)電壓控制策略及仿真研究[J]. 電力系統(tǒng)保護與控制， 2014， 42（11）： 21-27.

Chen J L， Zhang B， Lan Q， et al. Research on strategy and simulation of coordinated automatic voltage control for UHVDC/AC hybrid grid [J]. Power System Protection and Control，2014， 42（11）： 21-27. （in Chinese）

［8］??薛禹勝， 雷興， 薛峰， 等. 關于風電不確定性對電力系統(tǒng)影響的評述[J]. 中國電機工程學報， 2014， 34（29）： 5029-5040.

Xue Y S， Lei X， Xue F， et al. A review on impacts of wind power uncertainties on power systems[J]. Proceedings of the CSEE， 2014， 34（29）： 5029-5040.（in Chinese）

［9］??Dhabai P， Tiwari N. Effect of stochastic nature and location change of wind and solar generation on transmission lattice power flows[C]//2020 International Conference for Emerging Technology （INCET）. IEEE， 2020： 1-5.

［10］??Shi J， Lee W J， Liu X F. Generation scheduling optimization of wind-energy storage system based on wind power output fluctuation features[J]. IEEE Transactions on Industry Applications， 2018， 54（1）： 10-17.

［11］??王玲玲， 王昕， 鄭益慧， 等. 計及多個風電機組出力相關性的配電網(wǎng)無功優(yōu)化[J]. 電網(wǎng)技術， 2017， 41（11）： 3463-3469.

Wang L L， Wang X， Zheng Y H， et al. Reactive power optimization of distribution network considering output correlation of multiple wind turbines[J]. Power System Technology， 2017， 41（11）： 3463-3469.（in Chinese）

［12］??明杰， 向紅吉， 戴朝華， 等. 大規(guī)模風電接入的運行場景無功優(yōu)化評估[J]. 電網(wǎng)技術， 2016， 40（9）： 2737-2742.

Ming J， Xiang H J， Dai C H， et al. Operation scenario reactive power optimization assessment with large-scale wind farm integration[J]. Power System Technology， 2016， 40（9）： 2737-2742.（in Chinese）

［13］??Fang R M， Shang R Y， Wu M L， et al. Application of gray relational analysis to k-means clustering for dynamic equivalent modeling of wind farm[J]. International Journal of Hydrogen Energy， 2017， 42（31）： 20154-20163.

［14］??吳麗珍， 蔣力波， 郝曉弘. 基于最優(yōu)場景生成算法的主動配電網(wǎng)無功優(yōu)化[J]. 電力系統(tǒng)保護與控制， 2017， 45（15）： 152-159.

Wu L Z， Jiang L B， Hao X H. Reactive power optimization of active distribution network based on optimal scenario generation algorithm[J]. Power System Protection and Control， 2017， 45（15）： 152-159.（in Chinese）

［15］??林俐， 潘險險， 張凌云， 等. 基于免疫離群數(shù)據(jù)和敏感初始中心的K-means算法的風電場機群劃分[J]. 中國電機工程學報， 2016， 36（20）： 5461-5468， 5722.

Lin L， Pan X X， Zhang L Y， et al. The K-means clustering algorithm for wind farm based on immune-outlier data and immune-sensitive initial center[J]. Proceedings of the CSEE， 2016， 36（20）： 5461-5468， 5722.（in Chinese）

［16］??王成福， 梁軍， 張利， 等. 基于機會約束規(guī)劃的風電預測功率分級處理[J]. 電力系統(tǒng)自動化， 2011， 35（17）： 14-19.

Wang C F， Liang J， Zhang L， et al. Classified treatment of wind power predictive power based on chance constrained programming[J]. Automation of Electric Power Systems， 2011， 35（17）： 14-19.（in Chinese）

［17］??雷亞洲， 王偉勝， 印永華， 等. 基于機會約束規(guī)劃的風電穿透功率極限計算[J]. 中國電機工程學報， 2002， 22（5）： 32-35.

Lei Y Z， Wang W S， Yin Y H， et al. Wind power penetration limit calculation based on chance constrained programming[J]. Proceedings of the CSEE， 2002， 22（5）： 32-35.（in Chinese）

［18］??Zhang H， Li P. Chance constrained programming for optimal power flow under uncertainty[J]. IEEE Transactions on Power Systems， 2011， 26（4）： 2417-2424.

［19］??李永森， 楊善林， 馬溪駿， 等. 空間聚類算法中的K值優(yōu)化問題研究[J]. 系統(tǒng)仿真學報， 2006， 18（3）： 573-576.

Li Y S， Yang S L， Ma X J， et al. Optimization study on K value of spatial clustering[J]. Journal of System Simulation， 2006， 18（3）： 573-576.（in Chinese）

［20］??崔惟. 風電并網(wǎng)電力系統(tǒng)電壓無功控制的概率決策方法研究[D]. 重慶： 重慶大學， 2017.

Cui W. Probabilistic decision methods of voltage and reactive power control for wind power integrated power system[D]. Chongqing： Chongqing University， 2017. （in Chinese）

（編輯??詹燕平）