基于降階動態相量模型的電感耦合式勵磁系統間接勵磁電流估計

付興賀 夏宏偉 熊嘉鑫

基于降階動態相量模型的電感耦合式勵磁系統間接勵磁電流估計

付興賀 夏宏偉 熊嘉鑫

（東南大學電氣工程學院 南京 210096）

電勵磁同步電機（EESM）具有稀土永磁材料依賴性低、勵磁磁場可控、調速范圍廣的優點，在新能源汽車驅動領域擁有良好的應用前景。利用電感耦合式無刷勵磁技術可以有效降低傳統有刷EESM的摩擦損耗和維護成本。但是，無刷勵磁技術的引入導致勵磁電流無法直接測量，因此提出一種基于降階動態相量模型的間接式勵磁電流估計方法。首先利用電感耦合關系將勵磁電流的直接估計轉換為間接估計，有效地提高了算法的魯棒性；然后推導出勵磁電流降階動態相量估計模型，進一步提高間接估計方法的精度；接著考慮電流諧波影響，提出變系數改進方法；最后通過仿真和實驗驗證了估計方法的有效性。

電勵磁同步電機 電感耦合式無刷勵磁技術 電流估計 動態相量模型

0 引言

電勵磁同步電機（Electrically Excited Synch-ronous Machine, EESM）具有稀土永磁材料依賴性低、勵磁調節靈活、調速范圍廣等優點，在新能源汽車電驅動領域展現出特有的技術和成本優勢[1]。但傳統EESM的電刷集電環結構會引起摩擦損耗、增加維護成本、降低電機工作可靠性[2]。因此，無刷勵磁技術已成為EESM應用發展的迫切需求和亟待解決的關鍵問題[3]。現有無刷勵磁方式主要包括勵磁機式、諧波勵磁及無線電能傳輸式[4-6]。無線電能傳輸勵磁方式又可以分為電感耦合式和電容耦合式。其中，電感耦合式勵磁方法結構簡單、傳輸效率高，具有廣闊的應用前景[7]。

對于無刷勵磁系統，采用開環方式控制勵磁電流難以滿足EESM高精度勵磁磁場調節和速度控制要求，必須依靠勵磁電流反饋構建閉環控制系統才能提高勵磁電流的控制精度和抗干擾能力[8-9]。但無刷勵磁系統的勵磁繞組隨轉子一起旋轉，勵磁能量發送回路和接收回路之間無直接電氣連接，致使勵磁電流反饋的獲取面臨技術挑戰[10]。

無刷勵磁方案的差異和特點決定了勵磁電流獲取方法各有區別。在勵磁機方案中，可以根據勵磁機模型計算出勵磁機轉子的電壓、電流，再根據整流器模型計算勵磁電流估計值[11]。在諧波勵磁方案中，可以通過靜態實驗建立離線表格，根據定子諧波繞組電流估計勵磁電流[12]。電容耦合式勵磁方案比較特殊，勵磁靜止側和旋轉側共用同一電流回路，經過處理和折算便可直接獲得勵磁電流[13]。在電感耦合式勵磁系統中，獲取勵磁電流的方式包括：無線通信式、模型估計式。無線通信方式需要在二次回路增加采樣電路，利用無線通信裝置將采樣到的勵磁電流數據發送至一次回路[14]。該方法原理簡單，但是需要額外增加電路裝置，且傳遞的反饋信號易受到電機內磁場的干擾。模型估計方式包括基于電機繞組模型估計和基于線圈耦合電感模型估計。基于電機繞組模型的電流估計方式需要先建立電機繞組與勵磁繞組之間的磁鏈和電壓關系，再根據采集到的定子端電壓和電流計算出勵磁電流[15]；基于線圈耦合電感模型估計則需建立電感等效電路模型，利用一次電壓、電流信息計算出勵磁電流[16]。模型估計方式獲取勵磁電流對硬件要求較小，但是估計效果受數學模型精度及參數擾動的影響。

反映勵磁系統電路中物理關系的數學模型主要包括穩態模型和瞬態模型[17]。前者計算簡單但是精度較低；后者精度高但計算復雜。除此之外，還有精度較高且計算相對簡單的全階和降階動態相量模型[18]。但目前上述模型多用于無線電能傳輸系統建模和參數優化，鮮有研究將其應用于無刷電勵磁電機的勵磁電流估計。

針對模型估計中存在的參數擾動問題，文獻[19]提出一種利用母線電流修正勵磁電流估計值的方法，在一臺最大勵磁電流為18 A的樣機上進行驗證，變負載工況下的估計誤差在2%以內。該方法具有一定的估計精度，但是實現過程依賴大量實驗結果，普適性低，且需要增加一個電流傳感器用于檢測母線電流。文獻[20]利用一次側LCL型諧振補償結構的特點，提出一種適用于變負載工況的電流估計方法，并考慮了一次電流的諧波影響，在一臺額定勵磁電流為2 A的樣機上完成了實驗驗證，最終的電流估計誤差約為5.7%。該方法計算簡單，但受限于一次側特定的補償形式，需要用到兩個電流傳感器，且并未考慮負載參數變化對電流估計的影響。

鑒于此，本文針對串聯-串聯補償型電感耦合式無刷勵磁系統，提出了一種基于系統降階動態相量模型的間接勵磁電流估計方法，具有計算簡單、負載適應性強、硬件成本低等特點。本文首先設計了勵磁能量傳輸電路的拓撲結構，建立勵磁系統的等效電路模型；然后為避免負載參數擾動的影響，利用電感耦合關系，選取二次側反射電壓作為中間變量，提出一種間接式電流估計方法，建立降階動態相量估計模型，進一步提高間接估計方法的估計精度；接著考慮二次電流的諧波影響，提出變波形系數改進方法；最后通過仿真和實驗驗證了上述電流估計方法的有效性。

1 感應耦合式勵磁系統等效電路模型

根據電勵磁電機勵磁傳輸功率的要求，建立圖1所示的串聯-串聯感應耦合式無線電能傳輸系統的電路拓撲。該結構高階非線性的特性不利于勵磁電流的在線估計。但無刷勵磁系統正常工作時處于諧振狀態，可以采用基波分析法對系統非線性環節進行簡化并建立等效電路模型[21]，在一定誤差范圍內可以降低模型復雜度但又不失電流估計的有效性。

圖1 串聯-串聯補償型感應耦合式無刷勵磁系統結構

1.1 逆變器等效電路模型

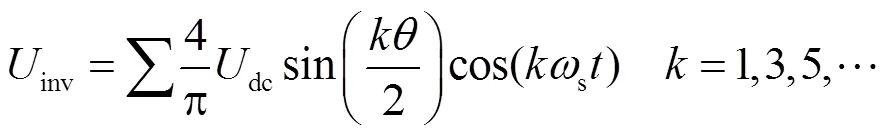
當母線電壓保持不變時，根據系統實際的移相角即可計算出逆變器輸出電壓的基波有效值。在后續分析中利用式（2）將非線性的逆變器環節等效為一個電壓源。

1.2 整流橋和負載等效電路模型

勵磁系統中作為負載的勵磁繞組端電壓滿足

圖2 整流橋和負載等效電路模型

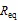
1.3 系統一次側等效電路模型

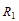
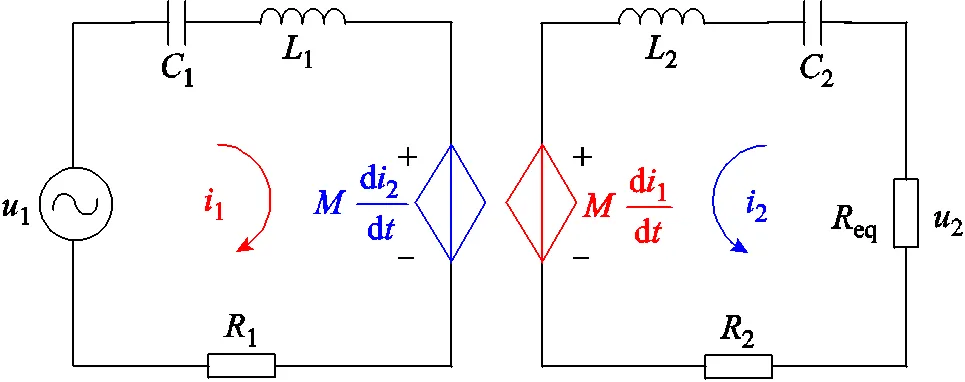
圖3 無刷勵磁系統等效電路模型

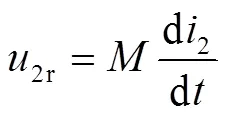
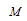
圖4 一次側等效電路模型

Fig.4 Equivalent model of wireless power transfer systems

利用一次側等效模型開展勵磁電流間接估計擺脫了對負載參數的依賴，提高了估計方法的魯棒性，同時降低了等效電路的儲能元件數量和模型階數。

2 降階動態相量估計模型

對于含諧振環節的系統，可以采用動態相量法進行數學建模，計算復雜度低于瞬態模型并且精度高于穩態模型，還可以進行降階處理簡化計算。本節將推導基于降階動態相量模型的勵磁電流估計數學表達式。

2.1 一次側等效電路降階動態相量模型

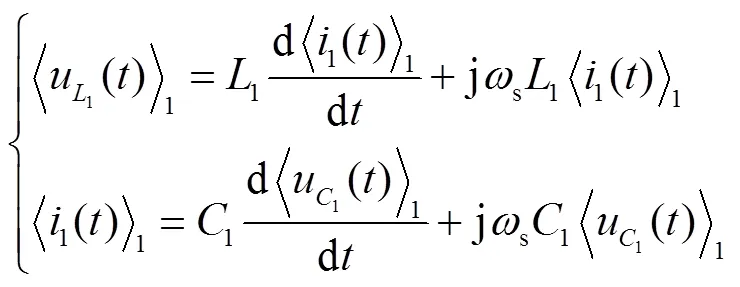
動態相量模型的每個狀態量對應兩個微分方程，分別為實部方程和虛部方程，因此系統一次側等效電路模型對應的全階動態相量模型為4階。為了方便計算，可以利用諧振網絡的特點對全階動態相量方程進行降階處理。根據式（7）寫出原始的諧振網絡動態相量模型在域下的表達式為

利用式（9）即可將諧振網絡的動態相量模型的階數由二階降為一階，如圖5所示。

降階動態相量模型精度高于穩態模型，計算復雜度遠低于瞬態時域模型。就模型本身精度而言，全階動態相量模型略微高于降階動態模型，但降階動態模型方程階數更低，計算簡單，更適用于在線計算[18]。因此本文基于降階動態相量模型來描述勵磁系統一次側等效電路，并在此基礎上推導出勵磁電流估計表達式。

一次側等效電路模型對應的微分方程為

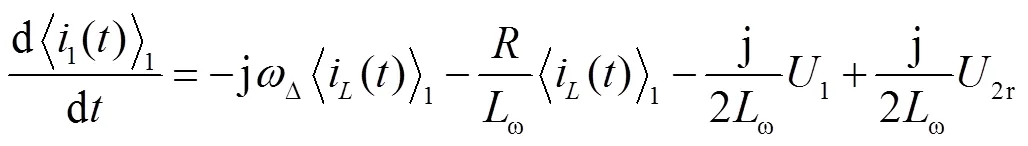
將方程中的實部和虛部進行分離，得

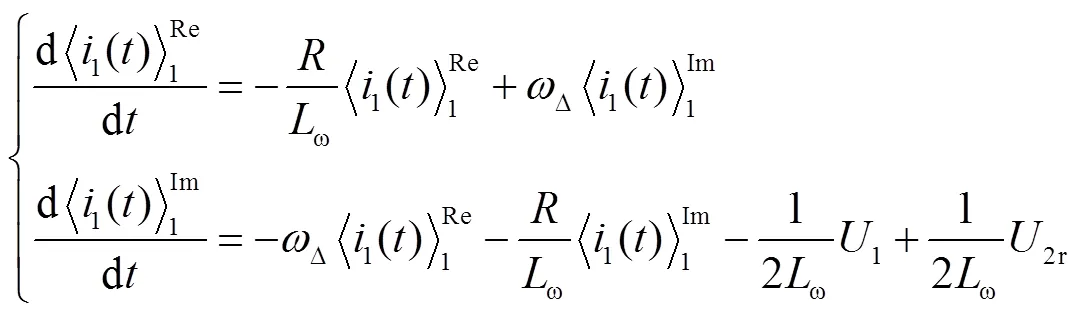
2.2 擾動觀測器設計

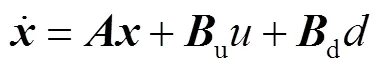
式中

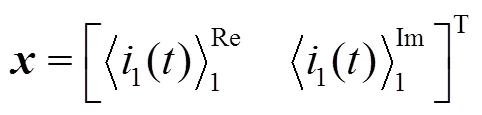
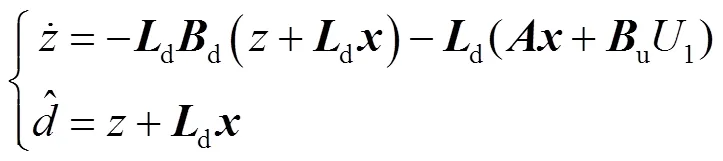
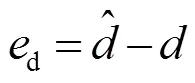
對式（16）兩邊進行求導并化簡可得

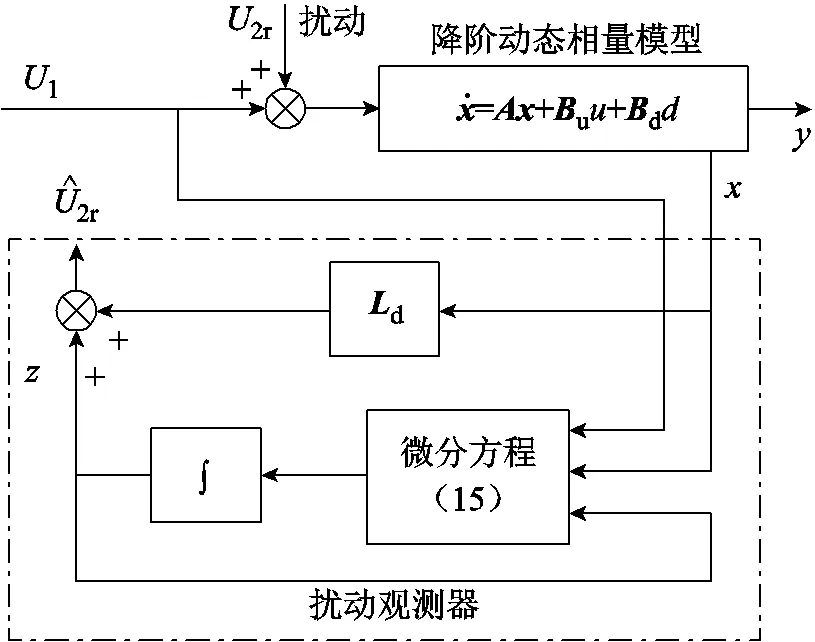
圖6 擾動觀測器結構框圖

2.3 勵磁電流估計值表達式

在動態相量模型中，擾動項二次側反射電壓可以表示為

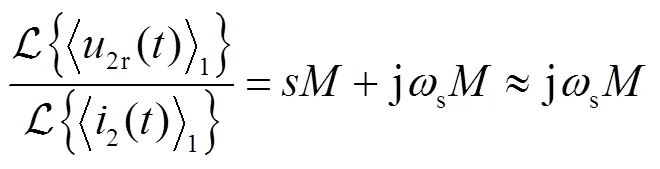
整理可得

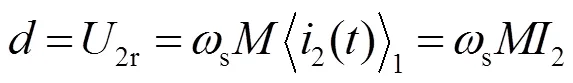
結合擾動觀測器輸出結果及式（4），可以寫出基于降階動態相量估計模型的勵磁電流表達式為

3 對比分析及改進

3.1 穩態估計模型和降階動態相量估計模型對比

為了更直觀地表現基于降階動態相量間接勵磁電流估計方法的效果，給出基于穩態模型的勵磁電流估計式用于對比分析。

結合一次側等效電路模型中各元件的穩態模型和基爾霍夫電壓方程，推導出基于穩態模型的勵磁電流估計表達式為

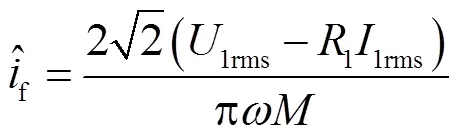
式中，1rms為一次電流有效值。

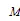
表1 無刷勵磁系統參數

Tab.1 Parameters of wireless excitation system

圖7 時兩種估計模型結果對比

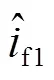
在不同溫度下，勵磁繞組電阻可由式（23）計算。

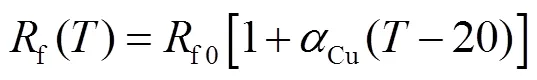
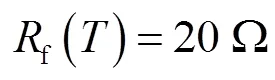
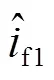
上述結果表明，本文所提的間接式估計方法是可行的，且相較于穩態估計模型，基于降階動態相量模型的估計方法具有更高的估計精度和魯棒性。

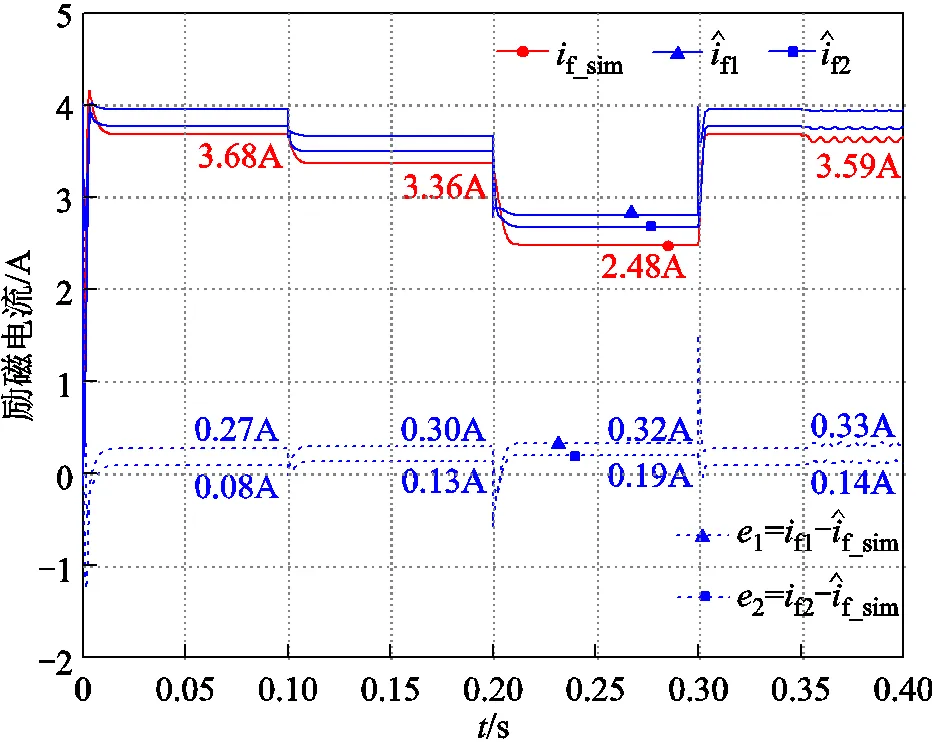
圖8 時兩種估計模型結果對比

3.2 考慮諧波影響的變波形系數估計方法

圖9 Rf =15 Ω時二次電流有效值及勵磁電流估計結果

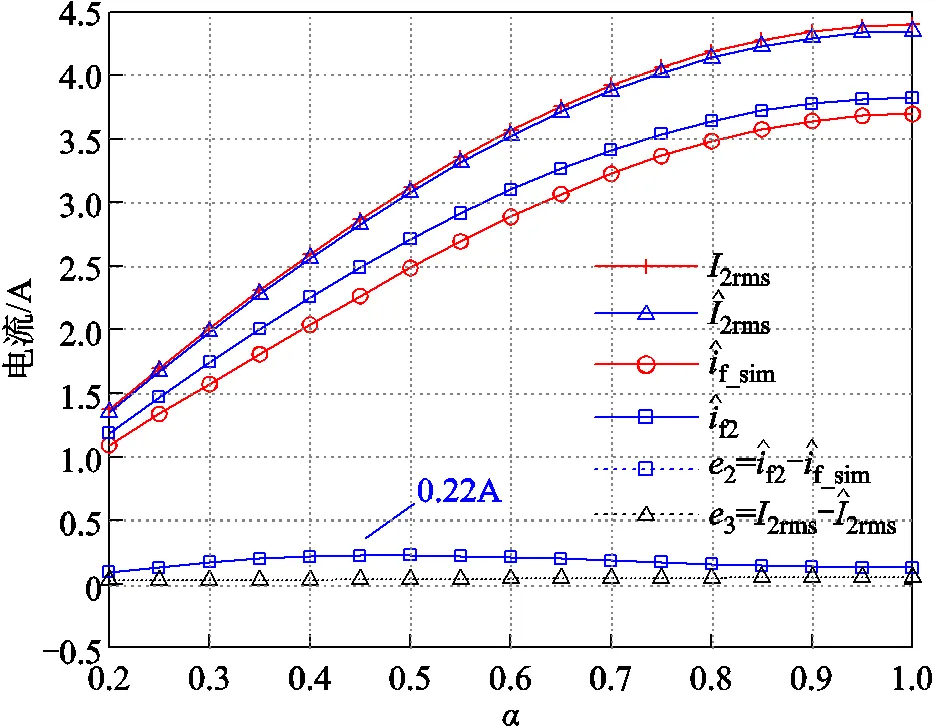
圖10 Rf =20 Ω時二次電流有效值及勵磁電流估計結果

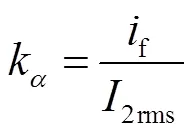
式（4）中基于基波假設的始終為0.9。但實際上受二次電流諧波影響，波形系數是一個與和相關的時變系數。不同工況下仿真計算得到的隨和變化曲線如圖11所示。

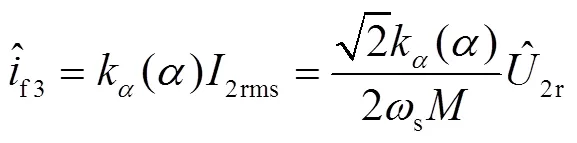
圖12 變系數勵磁電流估計結果

Fig.12 Results of variable coefficient estimator

圖13 時變系數勵磁電流估計結果

Fig.13 Variable coefficient estimation results when

綜上所述，基于降階動態相量模型的估計方法精度顯著高于穩態模型估計方法，并且采用考慮諧波影響的變波形系數改進估計方法可以進一步提高電流估計的精度和魯棒性。

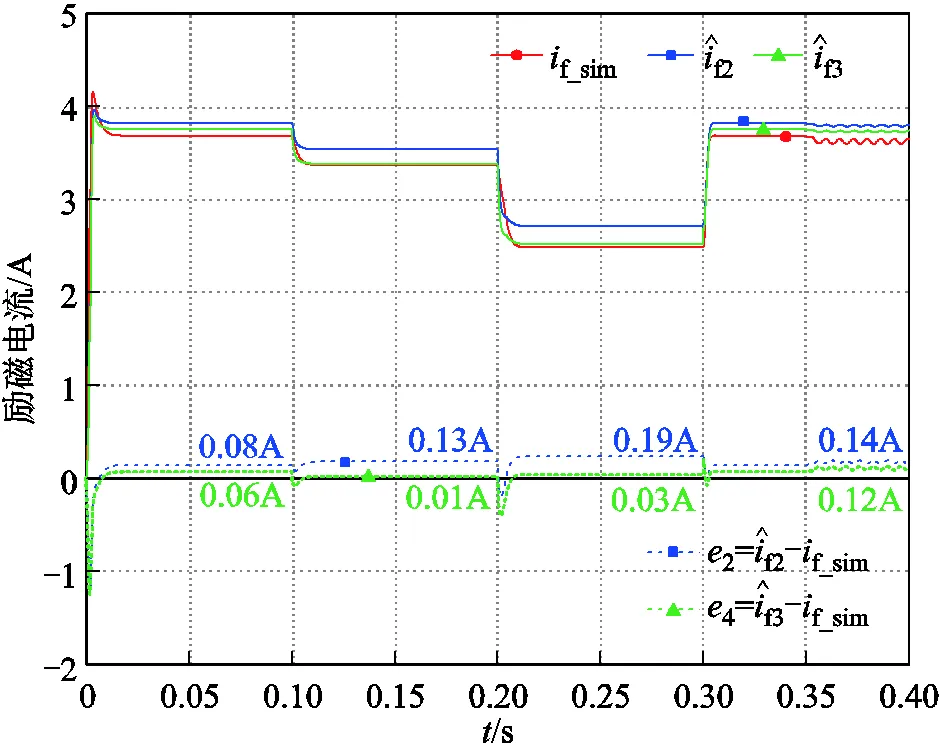
圖14 時變系數勵磁電流估計結果

4 實驗驗證

本文搭建的實驗平臺如圖15所示。

圖15 實驗平臺

為了獲取勵磁電流真實值來驗證電流估計效果，對電機轉子進行改造，利用電刷集電環將勵磁繞組引出，如圖16所示。

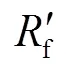
圖16 勵磁電流測量原理

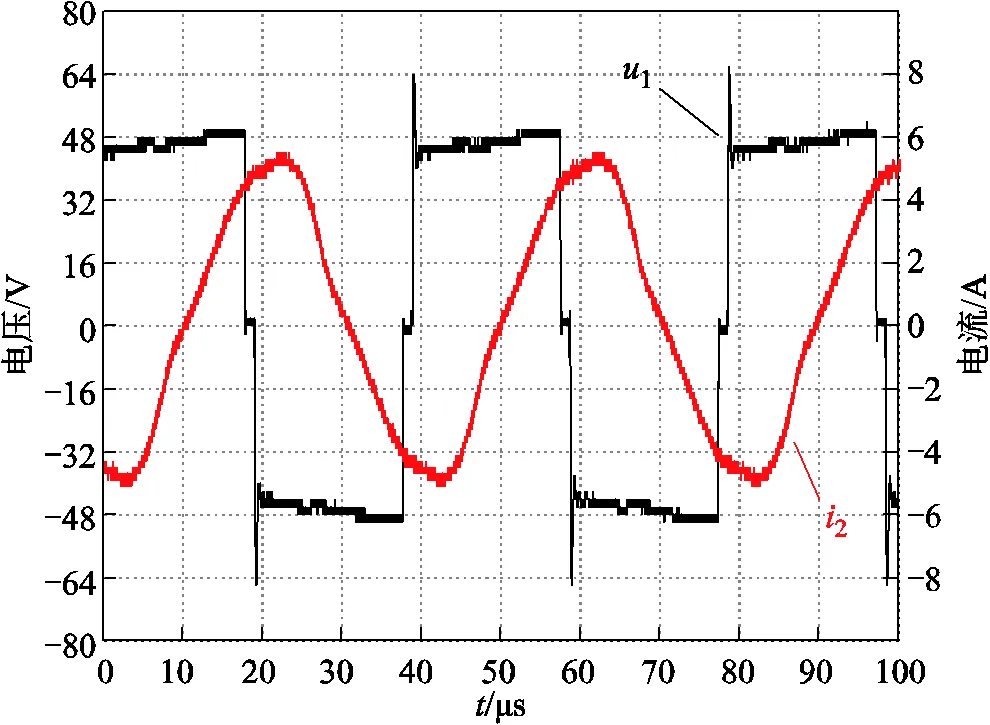
圖17 時的實驗波形

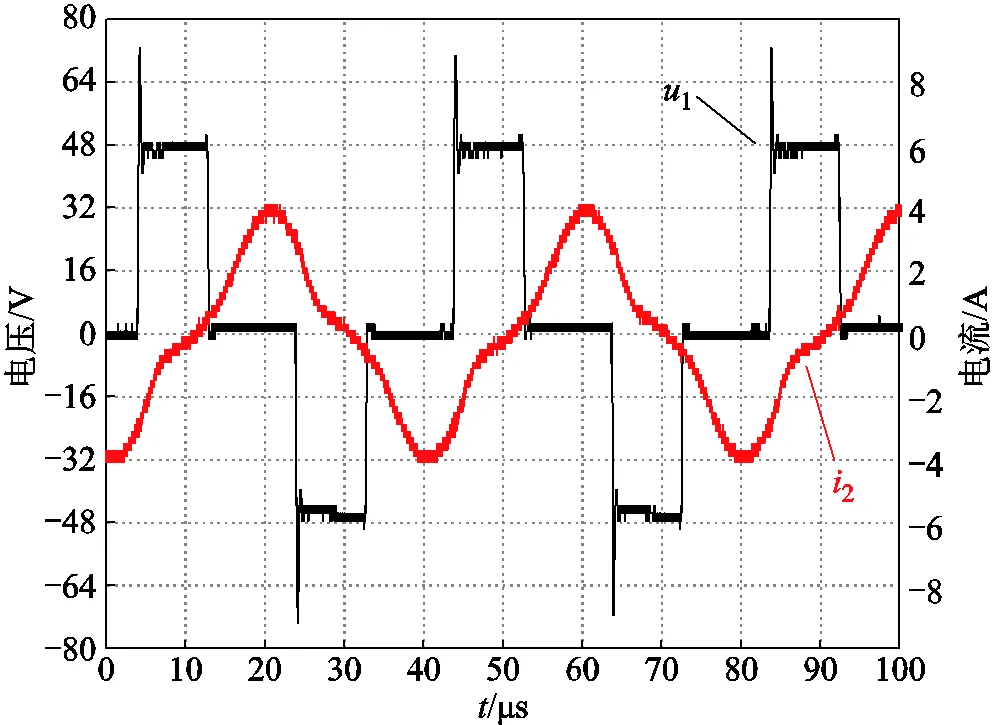
圖18 時的實驗波形

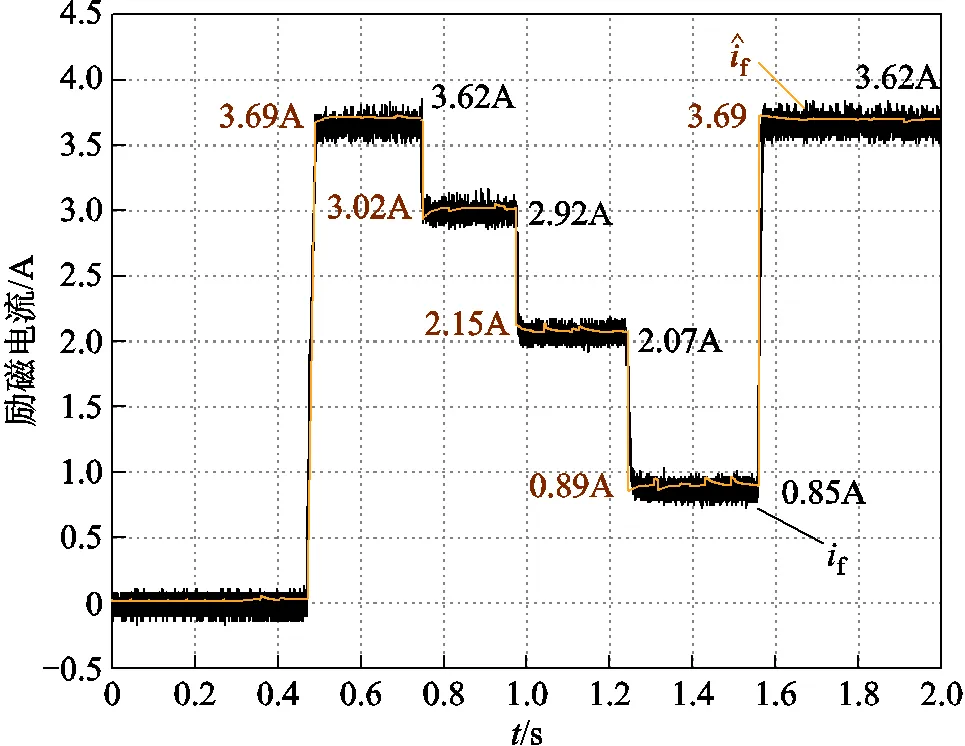
圖19 的勵磁電流跟蹤曲線

圖20 的勵磁電流跟蹤曲線

為了使勵磁電流估計結果更加平穩，增加了軟件濾波環節。圖19和圖20中曲線左側數值為勵磁電流估計值的平均值，右側數值為勵磁電流的平均值。結果表明，所提電流估計方法具有較高的精度和魯棒性，給定工況下最大相對估計誤差約為4.7%。

綜上所述，實驗結果與仿真結果基本一致，變波形系數改進方法的假設和應用都是合理的，所提的電流估計方法具有較高的精度和魯棒性。

5 結論

針對串聯-串聯補償型電感耦合式無刷勵磁系統，本文提出了一種基于降階動態相量模型的勵磁電流間接估計方法。該方法建立了勵磁系統的一次側等效電路模型，對勵磁電流進行間接估計，提高了估計方法的魯棒性；建立降階動態相量估計模型并考慮二次電流的諧波影響，提出變系數改進方法，進而獲得更高的電流估計精度。

本文所提的勵磁電流估計方法在串聯-串聯電感耦合勵磁系統中具有較好的效果，但對整流模型中的波形系數的細致分析和準確獲取還有待進一步的研究。此外，利用間接估計思想及動態相量模型，可以實現對更多非串聯-串聯型拓撲的電感耦合式勵磁系統高精度、高魯棒性的電流估計，拓寬所提電流估計方法的應用范圍。

[1] Fallows D, Nuzzo S, Galea M. Exciterless wound-field medium-power synchronous machines: their history and future[J]. IEEE Industrial Electronics Magazine, 2022, 16(4): 44-51.

[2] 寇佳寶, 高強, 滕詠哮, 等. 負載換流逆變器驅動電勵磁同步電機無速度傳感器模型預測控制方法[J]. 電工技術學報, 2021, 36(1): 68-76. Kou Jiabao, Gao Qiang, Teng Yongxiao, et al. Speed sensorless model predictive control for load commutated inverter-fed electrically excited synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 68-76.

[3] 付興賀, 江政龍, 呂鴻飛, 等. 電勵磁同步電機無刷勵磁與轉矩密度提升技術發展綜述[J]. 電工技術學報, 2022, 37(7): 1689-1702. Fu Xinghe, Jiang Zhenglong, Lü Hongfei, et al. Review of the blushless excitation and torque density improvement in wound field synchronous motors[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689-1702.

[3] 卿曉東, 蘇玉剛. 電場耦合無線電能傳輸技術綜述[J]. 電工技術學報, 2021, 36(17): 3649-3663. Qing Xiaodong, Su Yugang. An overview of electric-filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.

[5] Dajaku G, Gerling D. Self-excited synchronous machine with high torque capability at zero speed[C]// 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 2018: 1165-1171.

[6] Di Gioia A, Brown I P, Nie Yue, et al. Design and demonstration of a wound field synchronous machine for electric vehicle traction with brushless capacitive field excitation[J]. IEEE Transactions on Industry Applications, 2018, 54(2): 1390-1403.

[7] Maier M, Parspour N. Operation of an electrical excited synchronous machine by contactless energy transfer to the rotor[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3217-3225.

[8] Song Kai, Li Zhenjie, Jiang Jinhai, et al. Constant Current/voltage charging operation for series–series and series–parallel compensated wireless power transfer systems employing primary-side controller[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8065-8080.

[9] Zaghrini C, Khoury G, Fadel M, et al. Minimum copper losses per torque optimization on electrically excited synchronous motors for electric vehicles applications[C]//2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 2022: 661-666.

[10] Stancu C, Ward T, Rahman K M, et al. Separately excited synchronous motor with rotary transformer for hybrid vehicle application[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 223-232.

[11] Jiao Ningfei, Liu Weiguo, Zhang Zan, et al. Field Current estimation for wound-rotor synchronous starter–generator with asynchronous brushless exciters[J]. IEEE Transactions on Energy Conversion, 2017, 32(4): 1554-1561.

[12] Yao Fei, An Quntao, Sun Lizhi, et al. Optimization design of stator harmonic windings in brushless synchronous machine excited with double-harmonic-windings[C]//2017 International Energy and Sustainability Conference (IESC), Farmingdale, NY, USA, 2017: 1-6.

[13] Hagen S, Dai Jiejian, Brown I P, et al. Low-cost, printed circuit board construction, capacitively coupled excitation system for wound field synchronous machines[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 5358-5364.

[14] Zhong Wenxing, Ron Hui S Y. Charging time control of wireless power transfer systems without using mutual coupling information and wireless communication system[J]. IEEE Transactions on Industrial Electronics, 2017, 64(1): 228-235.

[15] Tang Junfei, Jiang Bowen, Boscaglia L, et al. Observations of field current and field winding temperature in electrically excited synchronous machines with brushless excitation[C]//2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 2022: 841-847.

[16] Berweiler B, Ponick B. Current and average temperature calculation for electrically excited synchronous machines in case of contactless energy supply[C]//2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 2020: 1730-1735.

[17] Chen Fengwei, Garnier H, Deng Qijun, et al. Control-oriented modeling of wireless power transfer systems with phase-shift control[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 2119-2134.

[18] Li Hongchang, Fang Jingyang, Tang Yi. Dynamic phasor-based reduced-order models of wireless power transfer systems[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11361-11370.

[19] Tang Junfei, Liu Yujing, Lundberg S. Estimation algorithm for current and temperature of field winding in electrically excited synchronous machines with high-frequency brushless exciters[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3512-3523.

[20] Kang Jinsong, Liu Yusong, Sun Liangrong. A primary-side control method of wireless power transfer for motor electric excitation[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi'an, China, 2019: 2423-2428.

[21] 鄭廣策, 趙凱, 王浩宇, 等. 基于LCC-S補償網絡的無線充電系統小信號模型[J]. 電工技術學報, 2022, 37(21): 5369-5376. Zheng Guangce, Zhao Kai, Wang Haoyu, et al. Small-signal model for inductive power transfer systems using LCC-S compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5369-5376.

[22] Kang Jinsong, Liu Yusong, Sun Liangrong, et al. A reduced-order model for wirelessly excited machine based on linear approximation[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12389-12399.

[23] Cao Pengju, Tang Yunyu, Zhu Fan, et al. An IPT system with constant current and constant voltage output features for EV charging[C]//IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 2018: 4775-4780.

[24] 趙進國, 趙晉斌, 張俊偉, 等. 無線電能傳輸系統中有源阻抗匹配網絡斷續電流模式最大效率跟蹤研究[J]. 電工技術學報, 2022, 37(1): 24-35. Zhao Jinguo, Zhao Jinbin, Zhang Junwei, et al. Maximum efficiency tracking study of active impedance matching network discontinous current mode in wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 24-35.

Indirect Field Current Estimation Algorithm for Inductively Coupled Excitation Systems Based on Reduced-Order Dynamic Phasor Model

Fu Xinghe Xia Hongwei Xiong Jiaxin

（School of Electrical Engineering Southeast University Nanjing 210096 China）

Electrically excited synchronous machines (EESM) has the advantages of low dependence on rare earth permanent magnet materials, controllable excitation field and wide speed regulation range, and has a good application prospect in electric vehicles. However, the traditional EESM's brush-slip ring structure caused friction loss, increased maintenance costs, and reduced reliability. Therefore, brushless excitation has become an urgent requirement and a critical issue to be solved for EESM applications. Inductively coupled brushless excitation technology can effectively reduce friction losses and maintenance costs. Currently, mainstream brushless excitation methods include exciter type, harmonic excitation type, and wireless power transfer type. Wireless power transfer excitation can be divided into inductive coupling and capacitive coupling types. Inductive coupling excitation has a simple structure and high transmission efficiency, making it promising for applications.

However, the usage of brushless excitation technology will bring a new challenges. The excitation winding of brushless excitation system rotates with the rotor, and there is no direct electrical connection between the transmitting circuit and the receiving circuit, resulting in the acquisition of excitation current value facing technical challenges. To estimate the field current in similar scenarios has been the scope of some previous studies. The existing current estimation methods can achieve good results in their respective application fields, but there are some limitations and shortcomings, which need to be further developed.

In view of this, an indirect excitation current estimation method based on reduced order dynamic phasor model is proposed for series-series compensation inductively coupled brushless excitation system, which has the characteristics of simple calculation, strong load adaptability and low hardware cost. The topology structure of excitation energy transmission circuit is designed. The equivalent circuit model of excitation system is established. In order to avoid the influence of load parameter disturbance, an indirect current estimation method is proposed by using the inductive coupling relation and the secondary side reflection voltage as the intermediate variable. A reduced order dynamic phasor estimation model is established to further improve the estimation accuracy of the indirect estimation method. Considering the harmonic effect of subside current, an improved method of variable waveform coefficient is proposed. Finally, the validity of the current estimation method is verified by simulation and experiment.

The proposed excitation current estimation method has a good effect in series-series inductively coupled excitation system. And only one current sensor is required, resulting in low hardware cost. However, the detailed analysis and accurate acquisition of waveform coefficients in the rectification model need further research. In addition, the indirect estimation idea and the dynamic phasor model can be used to estimate the current of more inductively coupled excitation systems with non-series-series topology with high accuracy and high robustness, and broaden the application range of the proposed current estimation method.

Electrically excited synchronous machines, inductively coupled brushless excitation technology, current estimation algorithm, dynamic phasor model

10.19595/j.cnki.1000-6753.tces.230946

TM341

國家自然科學基金資助項目（51977035）。

2023-06-23

2023-08-06

付興賀 男，1978年生，博士，副教授，研究方向為高溫特種電機及其控制、伺服系統多源異構擾動抑制。E-mail：fuxinghe@seu.edu.cn （通信作者）

夏宏偉 男，1998年生，碩士研究生，研究方向為電機控制。E-mail：220213084@seu.edu.cn

（編輯 赫蕾）