交織區微觀交通仿真模型參數敏感性分析

崔欣宇,宋霞飛,周晨靜

(北京建筑大學通用航空北京實驗室,北京 102616)

城市快速路承擔城市內部中、遠距離的空間銜接功能,是城市路網體系的骨架[1]。交織區是城市快速路系統的常見瓶頸點,其交通流運行組織相對復雜,是擁堵產生的常發地帶[1-2]。以交織區為代表的城市快速路瓶頸區域交通流運行特性及通行能力是研究的熱點與焦點問題[3-5]。

與其他道路基礎設施不同,交織區交通流運行特征受主線流量、匝道駛入流量及主線駛出流量三股車流相互作用影響,不同流量組合產生不同類別運行特征,致使交織區沒有基準通行能力。同時,交織區交通流運行研究需要聚焦整個交織區段,非單一斷面能夠表征其通行特性。由此,數據采集難度大成為制約交織區研究有效推進的難點[6]。微觀交通仿真技術能夠實現多參數、多變量組合作用下的交通流運行規律挖掘,逐漸成為研究復雜交通設施的有力工具[7]。

微觀交通仿真系統一般由多個子模型構成,包含跟馳、換道和橫向運動模型等,各子模型的參數共同影響車輛間的相互作用,控制單體車輛的運行行為,推演復雜交通系統中車輛作用過程[8]。仿真模型參數標定是保證模型準確性、有效性和不同情景適用性的必要環節,是科學應用微觀仿真技術的前提[8-9]。自20世紀90年代仿真技術應用于交通系統研究,微觀仿真模型標定方法不斷完善,研究者提出了詳盡可行的參數標定流程[8,10]。開展模型參數標定之前,需要明確模型標定參數集合,即進行微觀仿真模型參數對校核指標的敏感性分析工作,能夠有效地確定關鍵參數,以減少標定參數種類,提升工作效率[11-12]。交織區仿真模型參數標定是開展交織區微觀交通仿真研究的基礎,現聚焦微觀仿真模型參數敏感性分析方法對比分析、交織區流量狀態對參數敏感性分析結果影響、交織區微觀仿真模型參數選取等三個問題,設計并開展仿真實驗,以期對基于仿真技術的快速路交織區交通流特性深入挖掘提供借鑒。

1 仿真參數敏感性分析流程

通常,參數敏感性分析的步驟主要包含選定待分析參數、明確校核指標、設計仿真實驗方案、搭建路網仿真模型、賦值待分析參數、開展仿真實驗、匯總仿真實驗結果和分析模型參數敏感性。如圖1所示。

圖1 仿真參數敏感性分析流程

(1) 生成仿真實驗方案。為了保證實驗結果的有效性,在正式開始仿真實驗前需要合理、有效地設計實驗方案,包括待分析參數集合、校核指標、仿真實驗的次數及對應參數取值組合。需要注意選定仿真實驗次數時注意參數水平值的選取,保證生成具有統計意義上的數據結果。

(2) 輸出仿真實驗結果。根據生成的實驗方案搭建路網仿真模型,進行仿真模型參數賦值,一般可以采用編程語言調取仿真建模文件,對其語句進行修改。如VISSIM平臺的仿真建模文件為文本文件,可直接利用Python、VBA等語言修改文本字符,實現參數賦值。同時,也可調用微觀仿真平臺的COM接口,與仿真軟件進行協議通信。運行仿真文件時,仍可通過調用COM接口實現仿真程序的自動化運行,最后將仿真運行結果匯總。

(3)分析仿真參數敏感性。根據實驗方案選定敏感性分析方法,并對結果進行敏感性分析。研究時通常需要根據不同的實驗方案選取合適的敏感性分析方法。如單因素變化分析主要采用散點圖法判斷敏感性,參數全樣本空間取值則可以采取機器學習中適用于參數敏感性分析的方法。

2 仿真參數敏感性分析方法

交通仿真模型參數敏感性分析的方法有很多種,從因素數量和分析方法類別角度可大致分為統計分析方法和機器學習分析方法兩種形式,具體如圖2所示。

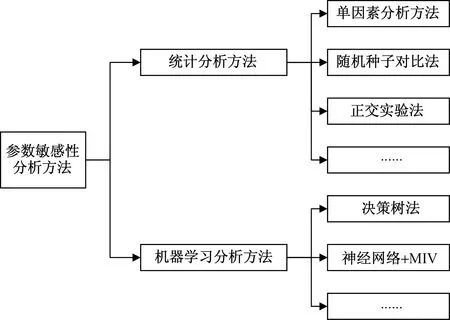
圖2 仿真參數敏感性分析方法

2.1 統計分析方法

(1)單因素分析方法。單因素分析方法即保持其他參數取值不變(一般采取默認參數值)時,僅改變可能對校核指標值產生影響的某一單一因素值,根據結果分析該因素對校核指標的敏感性程度。

現有研究中,學者多以單因素分析法對仿真模型參數進行敏感性分析[13]。單因素分析法一般采用散點圖或折線圖來表征校核指標隨待分析參數的變化趨勢。以此來定性地描述待分析參數的敏感性大小。

(2)隨機種子對比法[14]。隨機種子分析法是在仿真同一參數組合時,采用不同的隨機種子進行仿真,比較隨機種子和待校核參數對校核指標變化的影響程度,來判斷待校核參數的敏感性。

(3)正交實驗法[15]。正交實驗法則是用“正交表”來安排和分析全樣本實驗的一種數理統計方法,主要是通過比較少的實驗次數達到全面分析的實驗結果。通常把在實驗中待校核的各種參數的不同狀態稱為水平,每個參數都需要根據正交實驗表的設計規則去進行參數水平測試。通過正交表這種規格化表格在多次實驗中選出少數具有代表性(即敏感性較高)的參數。

2.2 機器學習分析方法

機器學習中有多種方法可以用來分析參數對于校核指標影響程度,即交通仿真模型中參數對校核指標的敏感性程度。包括決策樹法、BP神經網絡結合平均影響值(back propagation-mean impact value,BP-MIV)方法等。

2.2.1 決策樹分析方法

決策樹法進行學習時的關鍵是選擇最優劃分屬性。在決策樹每個結點位置,根據特征的表現通過某種規則分裂出下一層的葉子節點,終端的葉子節點即為最終的分類結果。形成對應決策樹后,通過基尼系數(Gini)對因子重要程度G進行判斷,并以因子重要程度來表征參數的敏感性程度。表達式為

(1)

式(1)中:t為給定的節點;i為標簽的任意分類;c為標簽總類別;p(i|t)為標簽分類i在節點t上所占的比例。

分裂葉子節點的規則主要包括信息增益最大、均方差最小等方法,這些方法可以用來衡量每次決策前后,信息混亂程度變化的情況。在進行多因子決策樹分析時,可以得到各因子對產生結果變化的重要性。

2.2.2 BP神經網絡與MIV結合分析方法

神經網絡根據特定算法學習仿真的實驗結果,經過不斷的迭代學習,生成在誤差允許范圍內的不同層之間的權值。此后,將訓練樣本P中每一個待分析參數在原值的基礎上分別加/減10%構成兩個新的訓練樣本P1和P2,再分別作為樣本代入已建成的網絡,得到兩個仿真結果A1和A2,二者的差值即為變動該參數后對校核參數的影響變化值(impact value,IV),最后將IV按訓練集數量平均即可得出該參數對校核指標的MIV,以此來表征待分析參數的敏感性程度。

交通仿真模型參數體系較為復雜,涉及多種參數需要進行敏感性分析,并針對敏感性較高的參數進行標定。不同交通場景則需要考慮不同的子模型。例如,通常研究者在進行單車道環境復現時,僅需要考慮跟馳模型中的參數。但在進行復雜場景仿真時,則跟馳模型和換道模型共20個待分析參數均需要考慮。交織區同屬復雜交通場景,在進行交通仿真參數敏感性分析時需要考慮多方參數,此時傳統的統計學方法實現起來就較為困難,如正交實驗法在面對多變量時則無法通過統計學軟件生成對應的正交表。而機器學習方法就會更加適用交織區這種影響因素較多的場景。因此,為全面分析交織區仿真參數的敏感性情況,根據搭建的交織區場景,保證除待分析參數外其他條件相同的情況下,分別采用單因素分析方法和全樣本分析方法中提及的兩種方法進行分析,具體實例見第3節內容。

3 交織區參數敏感性分析綜合研究

為全面分析交織區場景下各參數對校核指標的敏感性,實驗分別選取了低、中、高三種流量狀態。在指標的選取上考慮交織區的運行特性分析,考慮選取交織區交織速度、非交織速度、主線流率、駛入流率、駛出流率、車均延誤共六個指標作為分析對象。在分析方法層面,選取了最常用的單因素分析方法,和機器學習分析方法中的決策樹分析、神經網絡分析共三種方法,探討微觀仿真模型參數對宏觀交通流特性的作用。

3.1 方案設計

3.1.1 分析場景說明

研究選取A型交織區作為仿真場景,通過仿真實驗的設計表格開展建模分析。

(1)基礎條件。在仿真的場景搭建中,由于車道標準設計寬度為3.5 m,因此本次實驗均采用標準設計寬度,主線車流運行限制速度為80 km/h,仿真環境中涉及的其他道路幾何條件具體數值見表1,搭建路網模型如圖3所示。根據《公路通行能力手冊》,交織區長度300 m、交織流量比0.45時,交織區的通行能力為4 400 pcu/h[16]。采用該通行能力值的0.5、0.75和1作為低、中、高三種流量條件的具體數值。速度閾值及加、減速度曲線均采用林子赫等[17]利用工程實測數據標定結果,修改后曲線如圖4所示。

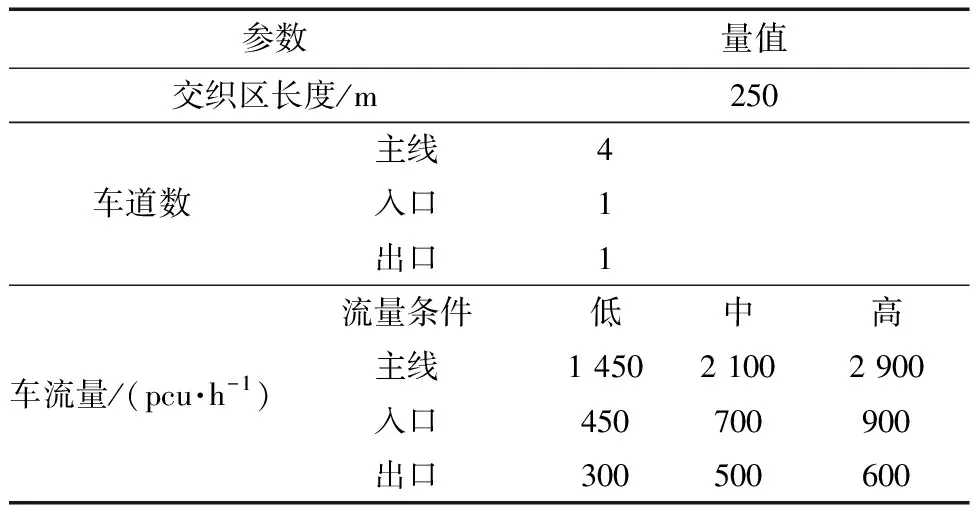
表1 交織區基礎條件

圖3 路網模型

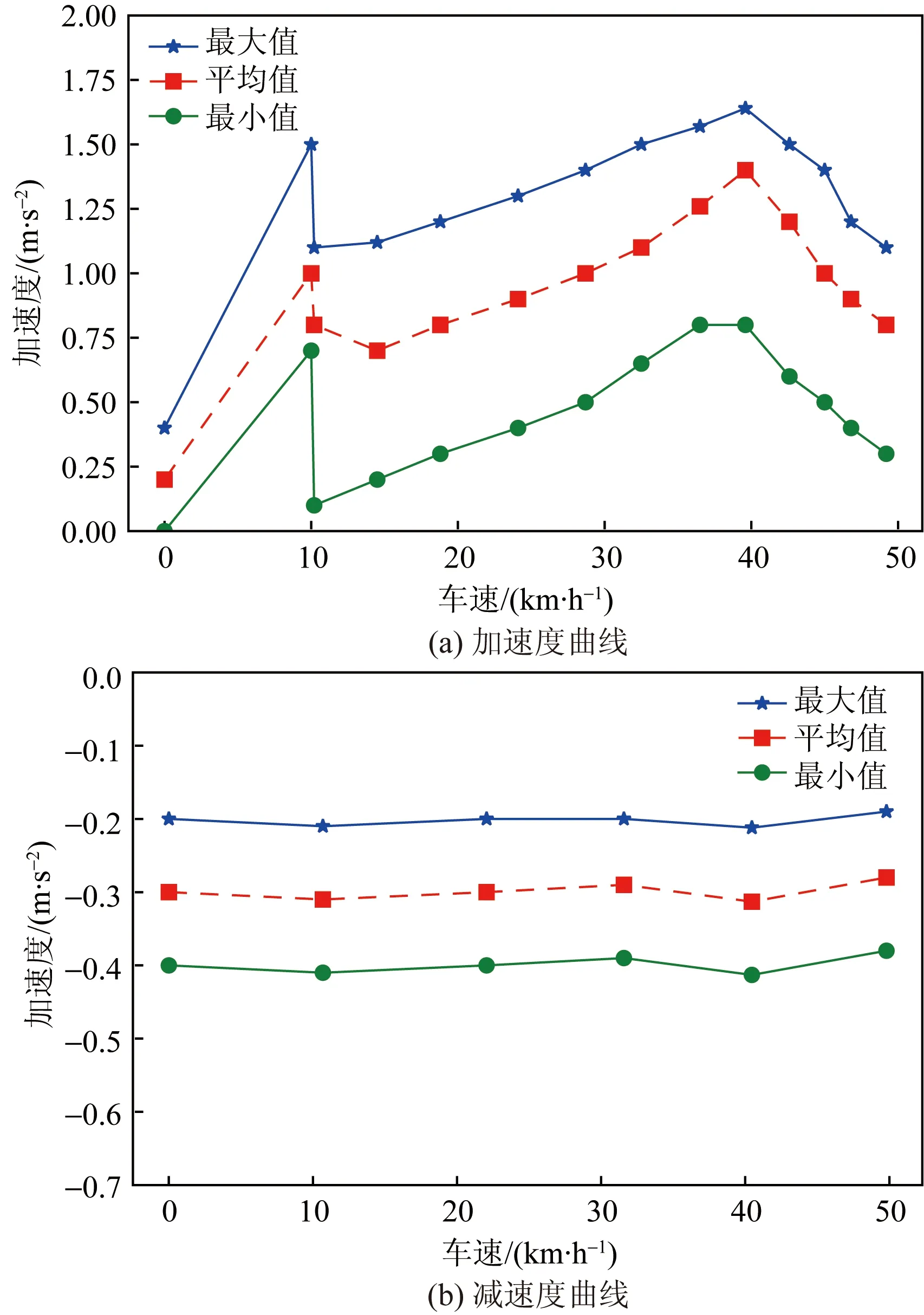
圖4 加、減速度曲線

(2)待分析參數。針對交織區這種復雜交通場景,全面考慮跟馳行為、換道行為模型和橫向運動模型。由于研究內容為快速路交織區,跟馳行為選擇適用于高速公路和城市快速路的W99跟馳模型,具體參數及取值范圍[9]見表2。仿真中的換道行為參數及取值范圍見表3。同時,對于橫向運動模型中菱形排隊選項和臨近車道車輛可視選項進行勾選,以體現仿真的真實性。

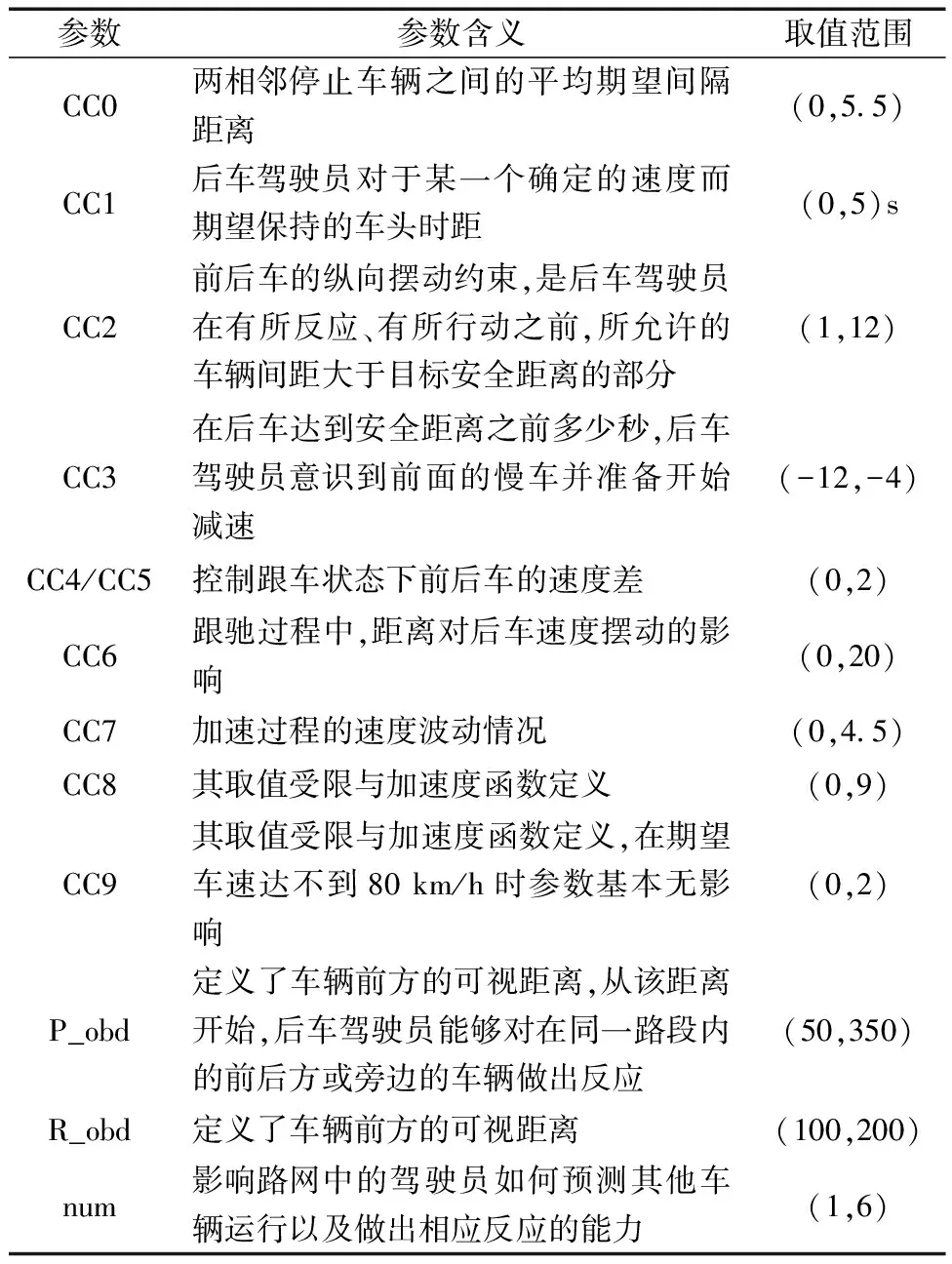
表2 跟馳模型參數

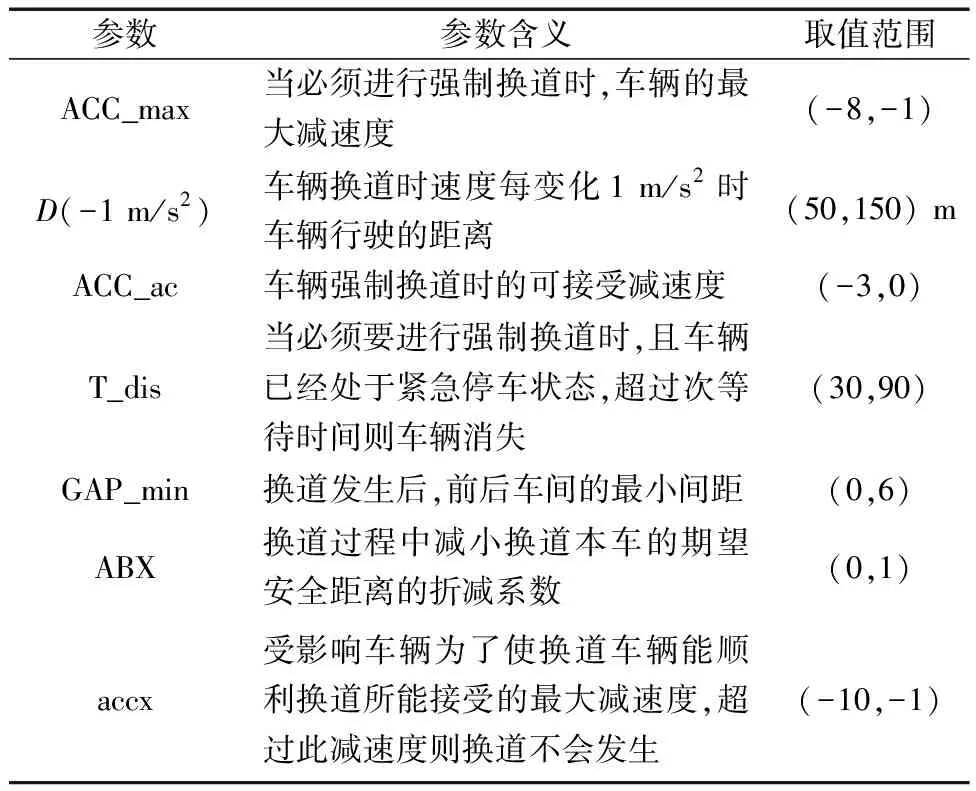
表3 換道模型參數

由于微觀交通仿真實驗仿真結果的變化由隨機種子、仿真參數變化兩部分因素導致。為消除系統隨機性造成的隨機誤差,每組仿真選取5個隨機種子進行實驗,分別為10、30、50、70、90,取其均值作為最終仿真結果,以減弱交通仿真系統隨機性帶來的實驗影響。

3.1.2 實驗方案說明

(1)統計分析方法實驗方案。本次采用單因素分析法開展實驗設計,需保持其他參數取值不變的情況下,僅改變其中一個待分析參數的取值。在表2和表3中設定的參數取值范圍內,等間隔取5個數值進行仿真實驗,共生成5×20=100組實驗,最終形成100×20的參數取值矩陣表。最后根據輸出結果繪制對應的折線圖,定性描述參數的敏感性。

(2)機器學習分析方法實驗方案。機器學習分析方法的實驗方案則是使每一參數均在其取值區間范圍內隨機產生N個取值水平,N取值應滿足大于參數總數30倍的要求。共生成20×30=600組實驗,最終形成600×20的參數取值矩陣表,每一行為一套參數取值組合。針對形成的實驗方案表格開展仿真實驗,獲取試驗結果。

得出仿真結果后,分別采用決策樹分析方法和BP神經網絡結合MIV分析方法進行敏感性分析,定量描述參數的敏感性。

3.2 敏感性分析結果

根據3.1中方案進行交通仿真實驗,其中統計分析方法共進行100×5組實驗;機器學習方法共進行600×5組實驗。根據仿真結果進行敏感性分析,具體結果如下。

3.2.1 單因素分析方法結果

根據實驗結果繪制各個參數在不同流量狀態下對速度、流率、延誤等指標的影響折線圖,即折線圖的變化趨勢定性描述不同參數的敏感性。可以發現不同參數根據流量條件下敏感性的不同可以分為三類,分別為所有流量狀態下參數均敏感、部分流量條件下參數敏感和不敏感。圖5所示為延誤在不同類別參數變化下的折線圖,其中圖5(a)為所有流量狀態下參數均對觀察指標有顯著性影響,圖5(b)為在部分流量狀態下參數對觀察指標有影響,圖5(c)為所有流量狀態參數均對觀察指標無影響。根據以上實驗結果進行因素相關性檢驗,以此表征參數敏感性強弱。圖6為低、中、高流量下的參數敏感性值。

圖5 單因素分析方法結果示例

3.2.2 機器學習分析方法結果

(1)決策樹方法。通常,決策樹中不同因子的Gini系數可表征其在樹中的重要程度,是判定因子對對應結果敏感性相對強弱的指標。在利用決策樹法計算得到各待分析參數對校核指標的敏感度,根據敏感度數值,生成如圖7所示的敏感性圖。

圖7 決策樹方法分析結果

(2)BP-MIV方法。利用MIV方法生成各參數對校核指標敏感性的數值,作為判定因子對結果敏感性強弱的指標,具體如圖8所示。

圖8 BP-MIV方法分析結果

3.3 實驗結果分析

根據第3.2節中三種分析方法得到的結果分別判斷文中分析的20個參數對校核指標是否具有敏感性。針對不同的分析方法,設定指標敏感性的具體標準。根據標準判定參數敏感性等級。并對判斷的結果從不同角度進行深入探討與分析。其中匯總結果如圖9所示。

①代表單因素方法分析結果;②代表決策樹方法分析結果;③代表BP-MIV方法分析結果

3.3.1 不同流量條件下參數敏感性情況

對仿真結果進行統計,低流量狀態下敏感性指數較高的有CC0、CC1、CC7、GAP_min、ABX這五個參數,其余參數沒有表現出對觀察指標較強的敏感性。主要是由于在流量較少時,車輛之間的交互行為也會隨之減少,部分車輛長期處于相對自由的行駛狀態,并不會出現跟馳或換道行為。

在中、高流量條件下,對觀察指標有敏感性的參數數量增多,且相對于高流量條件,中流量條件下具有敏感性的參數更多。出現這種現象,則是由于隨著流量的增多,交通流會有擁堵產生和擁堵消散的過程,在此過程中,車輛會出現大量交互行為,涉及到更多交通仿真子模型中的參數,導致結果中大量參數出現敏感性。而在流量增高到一定程度時,交通流會出現短期內無法消散的情況,即車輛持續擁堵在交織區域內,這時車輛之間的交互又會隨著車輛在瓶頸路段的積攢而減少。最終呈現出中等流量條件下參數敏感性個數最多的情況。

3.3.2 不同校核指標對參數的敏感性情況

通過結果對比可以發現,參數對不同校核指標的敏感性也不相同。其中運行速度方面,高流量狀態下的非交織速度敏感性參數數量要高于交織速度。而交織車道本應是車輛產生交互行為最多的位置,敏感性指標數量上卻沒有體現。這就需要考慮到高流量狀態下車輛的交織數量也隨之增大,這種增大會導致交織位置產生短期內無法疏解的擁堵,車輛行動困難。而非交織區域車輛換道行為則相對較少,車輛可以緩慢行駛,由此產生大量交互行為。

在中、高流量條件下,對延誤指標敏感的參數數量高于其他觀察指標,而低流量條件下則沒有明顯的展現出該特點。對于產生這種現象的原因做出如下分析:由于低流量條件下車輛基本處于自由行駛狀態,產生會造成延誤的情況極少,因此對延誤敏感性較高的參數數量也相對較少。

3.3.3 不同參數敏感性情況

分析實驗結果可得,跟馳模型中參數較為敏感的主要是CC0、CC1和CC7三個參數,這三個參數無論是在何種流量條件下都表現出較高的敏感性。CC4的敏感性則是在中、高流量條件下才體現出來。根據表2可知CC4是控制跟車狀態下前后車的速度差,而由于低流量時跟車行為較少,則可以解釋其在低流量時并未表現出敏感性的情況。

在換道模型中,GAP_min和ABX兩個參數在不同流量條件下均有較強敏感性。而ACC_max和D(-1 m/s2)兩個參數則在中流量條件下表現出較強的敏感性。通過表3可知ACC_max表示當必須進行強制換道時,車輛的最大減速度;D(-1 m/s2)則表示車輛換道時速度每變化1 m/s2時車輛行駛的距離。中流量條件下,車輛交互行為較多,且車輛仍能向前行駛,并沒有像高流量時車輛會長期處于擁堵狀態。因此在換道時為進入目標車道,會根據目標車道車輛運行情況調整自身速度,發生加減速行為,引起上述參數敏感。

4 結論

交織區作為復雜交通環境,需要考慮到交通仿真模型中較多子模型,包括跟馳模型、換道模型與橫向運動模型,敏感性分析過程較為復雜。且由于不同流量條件下車輛運行情況不同,研究分設三種流量條件,針對六個校核指標對交織區環境下的參數進行敏感性分析。得到如下主要結論。

(1)機器學習分析方法能夠在參數全樣本空間內隨機組合,相比單因素統計分析方法,得到的敏感性分析結果更為全面。尤其是決策樹分析方法分析過程簡單,利于程序化實現,能夠大幅度提升參數敏感性分析效率。

(2)低、中、高不同流量狀態對交織區微觀仿真模型參數敏感性作用有著不同影響。中、高流量狀態更能體現出仿真模型參數的作用,低流量狀態則出現部分參數敏感性弱的現象。但存在一部分模型參數,在低、中、高流量狀態下均有著較強敏感性,VISSIM平臺中CC0、CC1、CC7、GAP_min、ABX,這五個參數在不同流量狀態下都對車輛運行具有較強的敏感性。在開展交織區仿真模型參數標定時,建議選取接近飽和的流量狀態,才能標定出較好模型。

(3)相比于速度、流率指標,延誤指標具有更多的敏感性參數,尤其是在中、高流量條件下。主要原因在于延誤指標綜合性更強,更適宜選取為模型參數標定的校核指標。在開展交織區仿真模型參數標定時,建議選取延誤指標作為校核指標。