基于改進天鷹優化器的抱桿結構優化

方林,蔣曉琳,周慶豐,周煥林

(合肥工業大學土木與水利工程學院,合肥 230009)

抱桿是輸電鐵塔組立的重要起重工具,鐵塔輸送電壓的提升要求輸電鐵塔的高度和重量增加,從而導致抱桿的高度及鋼材尺寸隨之增加。在滿足工程使用的前提下,對抱桿進行優化設計顯得尤為重要,不僅減少了運輸過程的碳排放,也減少了在此方面的經濟支出。

元啟發式算法因其原理簡單、方便,被廣泛應用于測控技術、車輛工程、燃油轉輸、電力建設、航空航天等領域。于燕南等[1]使用鏡面反射算法優化橋式起重機的金屬結構,在滿足規范要求的同時減輕了結構的重量。周潼等[2]對遺傳算法進行改進,并應用于羅氏線圈結構的設計,構建了羅氏線圈優化系統。孟建軍等[3]使用模擬退火遺傳(simulated annealing-genetic algorithm,SA-GA)混合算法對車輛輪重分配問題進行優化設計,并將數值計算結果與仿真結果對比,驗證其理論計算結果的準確性。Wang等[4]通過響應面法建立賽車尾翼的近似模型,針對此模型使用遺傳算法優化賽車尾翼的升力阻力比。龔昊[5]對差分進化算法進行改進,并對燃油轉輸參數進行優化設計,得到燃油轉輸參數最優方案。陶然等[6]采用響應面法模擬抱桿的真實響應,使用改進的算術優化算法對抱桿的響應面代理模型進行優化設計,降低了計算成本。Khodzhaiev等[7]提出二階突變方法處理變長基因組來對遺傳算法進行改進,并使用改進的遺傳算法對輸電塔進行拓撲、形狀和尺寸優化。駱烜赫等[8]使用粒子群算法對功能梯度多級加筋圓柱殼進行輕量化設計,并進行有限元特征值屈曲分析驗證此優化結果。

天鷹優化器(aquila optimizer,AO)[9]作為當前較新的元啟發式優化算法,因其較好的計算能力被應用于科學研究的多個方面。Abd Elaziz等[10]將AO和深度學習相結合,用于提升2019年冠狀病毒病的圖像分類; Ma等[11]結合準對位學習策略和小波突變策略對AO進行改進,進行中國農村人口預測; Kharrich等[12]將AO結合算術優化算法,用于設計儲能系統的微電網。上述研究表明了AO計算能力的有效性,但該算法局部搜索能力不足,易停滯于局部最優,并且在空間桁架結構優化方面的研究還有待拓展。

現針對AO較弱的局部搜索能力,使用改進型Logistics混沌映射初始化算法的種群,有效幫助算法脫離局部最優[13];引入新的平衡搜索方式,全局搜索和局部搜索得到了更好的平衡,算法迭代后期仍具有廣泛的搜索能力,提升算法擺脫局部最優的能力;新的非線性參數增強算法的局部搜索能力;加入改進型反向學習策略,增加種群多樣性,防止算法陷入局部最優[14]。然后將改進的天鷹優化器(improved aquila optimizer,IAO) 結合罰函數法和有限元方法對十桿平面桁架結構和抱桿結構進行優化設計。

1 抱桿結構有限元分析

1.1 抱桿簡介

以白鶴灘-江蘇±800千伏特高壓直流輸電工程中使用的750截面落地雙搖臂抱桿建立有限元模型,如圖1所示,抱桿結構主要包括主桿段(普通段和加強段)、搖臂段和桅桿段。回轉支座,腰環拉線、調幅繩、內拉線等均為次要結構。

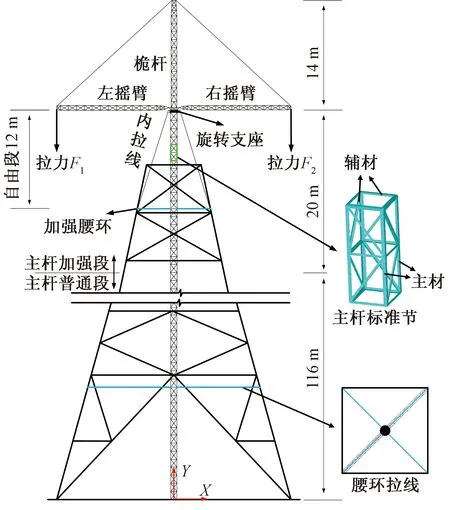
圖1 抱桿整體示意圖

該抱桿全高150 m,主要由抱桿主桿普通段(116 m),主桿加強段(20 m),搖臂(14 m)和桅桿(14 m)4個部分組成。抱桿主桿段和桅桿段截面為750 mm×750 mm,搖臂段截面為500 mm×600 mm,搖臂和桅桿頂部均采用變截面設計。抱桿回轉支座處設置內拉線,與抱桿鉛垂線的夾角為20°。抱桿自由段高12 m,抱桿與鐵塔間設置9道腰環,其中第一道為加強腰環,距離第二道普通腰環為12 m,其余腰環間距小于等于15 m。

抱桿最初設計的構件尺寸如表1所示,主材采用Q345鋼,輔材采用Q235鋼。密度ρ=7.85×103kg/m3,彈性模量E=2.06×1011Pa,泊松比υ=0.3。

表1 抱桿各段角鋼型號

1.2 抱桿有限元模型

為了方便建模,做以下約定。搖臂方位:搖臂俯視圖與X軸正向所成的角度;風向:X軸負方向的風向為0°,垂直X軸的風向為90°,二者角平分線為45°方向。如圖2所示。

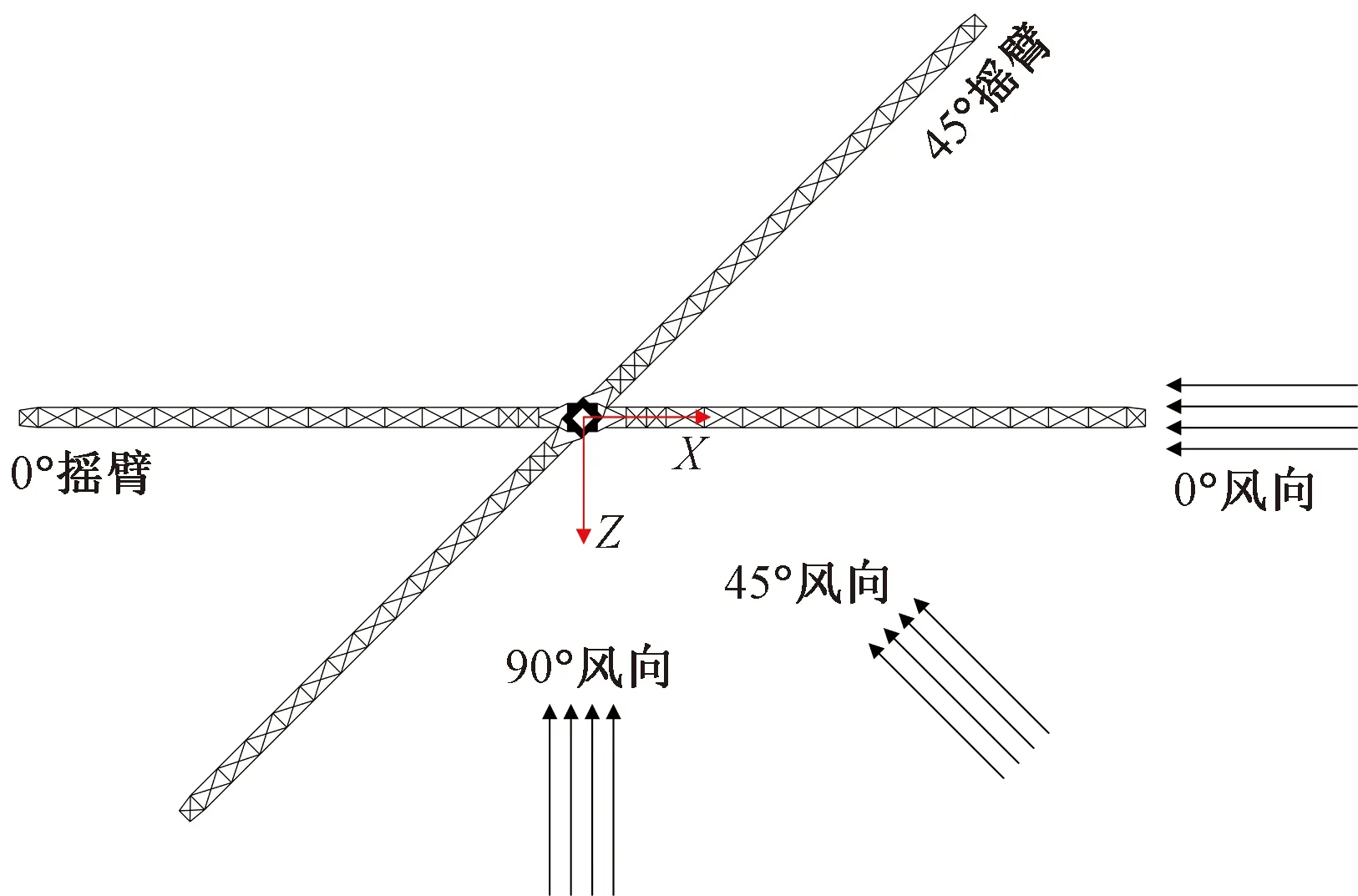
圖2 搖臂方位和風載荷方向

在抱桿三維有限元分析模型中采用梁單元模擬抱桿的主桿、桅桿和搖臂;用索桿單元模擬僅受拉力的內拉線和腰環等。釋放搖臂繞Z軸轉動的自由度。

1.3 荷載工況

抱桿承受的主要載荷包括自重、風載荷以及吊重。抱桿一側吊重為4 t,另一側為3 t,45°搖臂,45°風向時為此工程中的最危險工況。吊鉤重250 kg,起吊鋼絲繩重500 kg;最大工作風速13.8 m/s(6級風)。

根據《起重機設計規范》(GB 3811—2008)風載荷的計算公式為

Pw=CPA

(1)

C=1.7(1+η)

(2)

(3)

式中:C為風力系數;A為迎風面積;P為風壓;η為擋風折減系數,由充實率φ確定;Vs為計算風速。

1.4 有限元分析

采用有限元方法對落地雙搖臂抱桿最危險工況進行分析計算,分析結果如表2所示。由表2可知,在最危險工況下,主材的最大Mises應力為158.80 MPa,輔材的最大Mises應力為115.60 MPa,兩者均滿足《架空輸電線路施工機具基本技術要求》(DL/T 319—2018)中2倍屈服安全系數的要求;抱桿頂端最大水平位移為342.98 mm,抱桿屈曲系數為4.37,兩者均滿足設計要求。本文中將其作為優化工況對抱桿結構進行優化。

表2 最危險工況分析結果

2 改進的天鷹優化器

2.1 天鷹優化器

AO是Abualigah等[9]在2021年提出的一種元啟發式算法,該算法模擬天鷹這種生物的四種捕獵行為產生4個迭代公式,若當前迭代次數小于最大迭代次數的2/3,使用前兩個迭代公式進行全局搜索,否則采用后兩個迭代公式進行局部搜索。

2.1.1 第一種捕獵行為X1(擴大探索)

天鷹在高空中廣泛地探索,并通過垂直彎腰的高空飛翔識別獵物所在區域,來選擇出最佳狩獵區域。該行為表示為

X1(t+1)=Xbest(t)L+[XM(t)-Xbest(t)]rand

(4)

(5)

式(4)中:t為當前迭代;T為最大迭代次數;Xbest(t)為第t次迭代之前獲得的最佳解,即當前的最佳獵物位置;rand為0～1的隨機值;L為隨迭代次數的線性遞減值。XM(t)表示第t次迭代當前解的平均值,計算公式為

(6)

式中:D表示問題的維度;N表示候選解的個數(種群大小)。

2.2.2 第二種捕獵行為X2(縮小探索)

當天鷹在高空中發現獵物區域,會在獵物上方區域盤旋,準備著陸和發動攻擊。在該行為中天鷹會仔細地探索目標所在區域,從而為攻擊做準備。該行為表示為

X2(t+1)=Xbest(t)Levy(D)+XR(t)+

(y-x)rand

(7)

(8)

(9)

(10)

式中:XR(t)表示第t次迭代時在種群[1,N]范圍內的一個隨機解;Levy(D)為Levy飛行分布函數;y和x為搜索過程中的螺旋形狀參數;D表示問題維度;s=0.01;μ和υ為0～1的隨機數;β=1.5;r1為1～20的固定的搜索周期數;U=0.005 65;D1為從1～D的整數;ω為0.005;θ1=1.5π。

2.1.3 第三種捕獵行為X3(擴大開發)

當天鷹確定獵物所在區域,準備著陸和攻擊時,會垂直下降進行初步攻擊,以發現獵物的反應。在這里,天鷹將利用選定的目標區域來接近獵物并攻擊。該行為表示為

X3(t+1)=[Xbest(t)-XM(t)]α-rand+

[(BU-BL)rand+BL)δ

(11)

式(11)中:α和δ為一個確定的較小的開采調整值,值為0.1;BL為問題的下界值;BU為問題的上界值。

2.1.4 第四種捕獵行為X4(縮小開發)

當天鷹接近獵物時,會根據獵物的隨機運動在陸地上攻擊獵物。該行為表示為

X4(t+1)=QFXbest(t)-[G1X(t)rand]-

G2Levy(D)+randG1

(12)

(13)

式中:QF為平衡搜索策略的質量函數;G1為天鷹的各種運動,用于跟蹤奔跑期間的獵物;G2為2～0的線性遞減值。

2.2 改進的天鷹優化器(IAO)

2.2.1 混沌映射

AO的首代種群是以隨機化方式生成。混沌映射與隨機化相比,其產生的首代種群在搜索空間內分布更加均勻,幫助算法規避局部最優和算法早熟現象。毛清華等[13]提出的改進型Logistics混沌映射(improved logistic mapping,ILM)相比于經典Logistics混沌映射在初始化種群分布方面性能更佳,所以本文中使用改進型Logistics混沌映射初始化天鷹種群。計算公式為

(14)

Xij=yn(BU,j-BL,j)+BL,j

(15)

式(15)中:BU,j和BL,j分別為第j維搜索空間中的上界和下界,i∈[1,N],j∈[1,D],N和D分別為算法種群數和維度。

將得到的混沌序列[yn]代入式(15)得到天鷹種群的初始位置。

2.2.2 新的平衡搜索策略

在AO中,若當前迭代次數t≤2T/3時,算法進入全局搜索階段,反之進入局部搜索階段,為了更好地平衡兩者,擺脫局部最優值,本文提出一種新的平衡方式,公式為

(16)

式(16)中:E為隨迭代次數變化著的振蕩型參數。

當E>0.2時,算法進行全局搜索,否則進行局部搜索。如圖3所示,算法在迭代中期也可進行局部搜索,使得算法在搜索空間內搜索得更加徹底;在迭代后期保留局部搜索方式的同時加入全局搜索,使得算法在迭代后期仍具有廣泛搜索的能力,幫助算法規避局部最優。

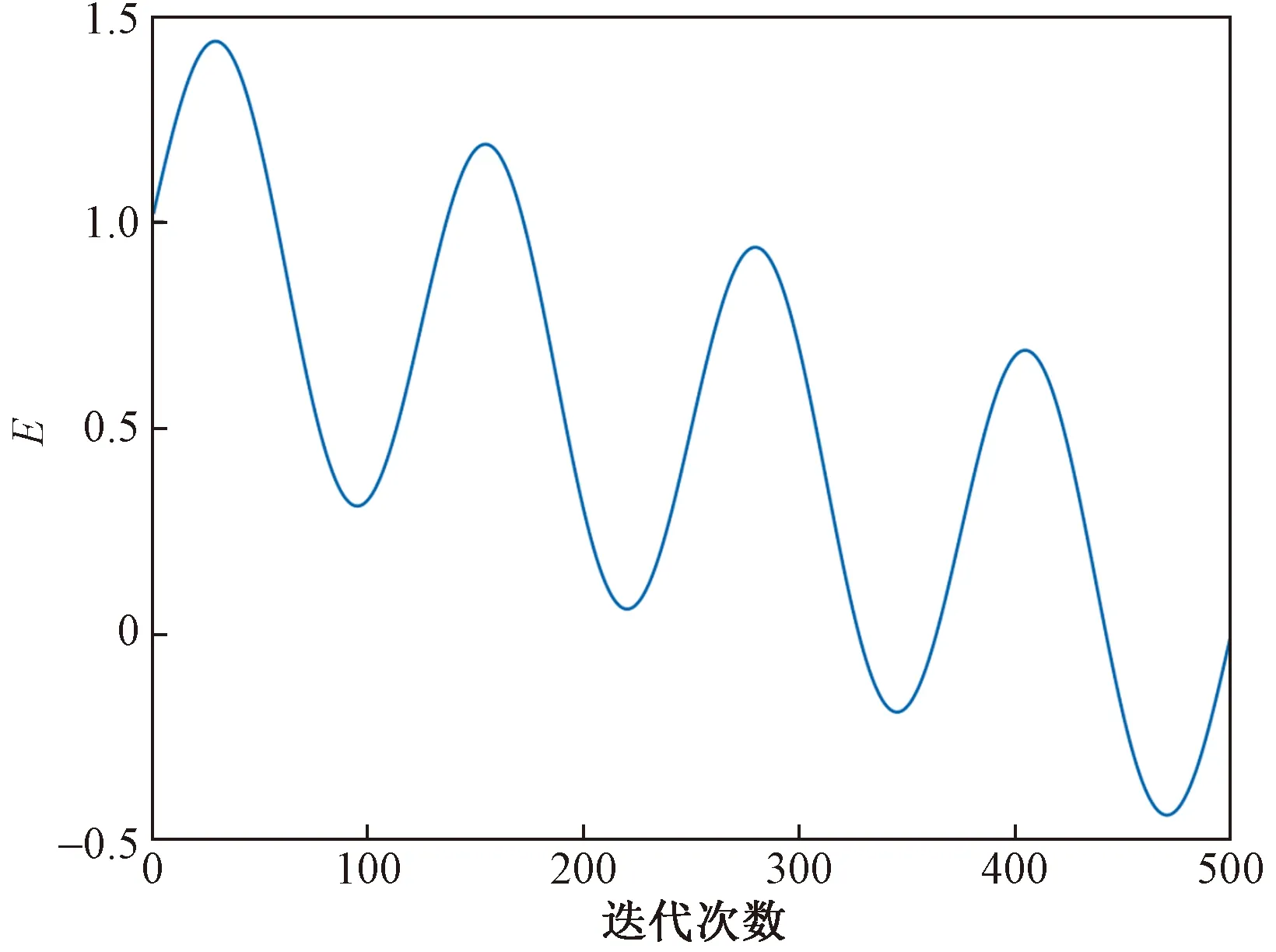
圖3 E值迭代曲線

2.2.3 參數G2的調整策略

G2是一個從2線性遞減到0的參數,代表天鷹跟蹤獵物時從第一個位置到最后一個位置的飛行斜率。本文提出一種非線性遞減參數,迭代曲線如圖4所示,即將式(13)中的G2調整為

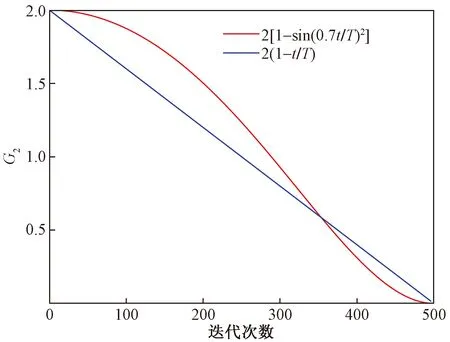
圖4 G2值迭代曲線

(17)

基于新的平衡方式,算法在迭代中期就進行了局部搜索,此時改進的G2具有較大的值,使得算法更加依賴Levy飛行,從而更加徹底的搜索解的空間;在迭代后期改進的G2較小,受Levy飛行隨機大范圍搜索的影響小,因此上一步得到的最優解Xbest(t)和歷史解X(t)將更加影響這一步的搜索結果,提升了迭代后期的局部搜索能力。

2.2.4 改進的反向學習策略

反向學習策略[15](opposition-based learning,OBL)是指在算法迭代過程中,利用當前解的位置產生一個對應的反向位置,然后比較當前解及其反向位置的適應度值,假如反向位置的適應度值優于當前解,則用反向位置代替當前解的位置,利用反向位置進入下一步的求解。

改進的反向學習[14](improved opposition-based learning,IOBL)公式為

(18)

式(18)中:xij(t)為當前解的位置;aj(t)為當前解第j維的上界;bj(t)為當前解第j維的下界;k1、k2均為0～1之間的隨機數。

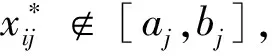
(19)

采用改進的反向學習策略,在算法探索階段后產生反向位置,增加了種群的多樣性,保證了算法在進行開發階段之前擁有更好的當前解,極大地幫助算法跳出局部最優,提升算法的計算精度。

2.2.5 IAO的基本流程

IAO的基本流程圖如圖5所示。

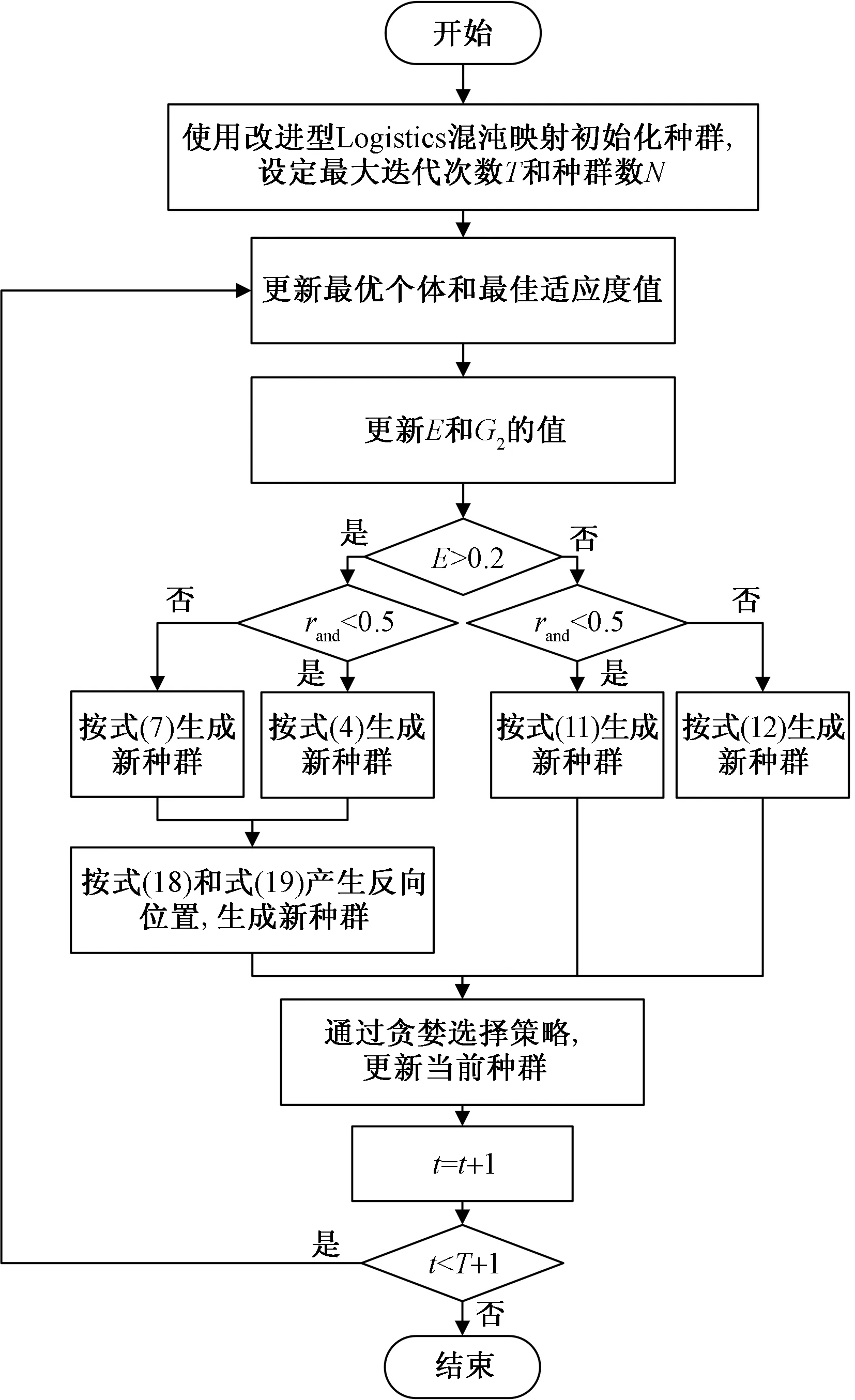
圖5 IAO優化流程圖

3 十桿平面桁架結構的優化

為了檢驗IAO在處理桁架結構離散型優化設計方面的能力,將IAO應用于十桿平面桁架結構的尺寸優化。十桿平面桁架結構如圖6所示,桿件和節點依次進行了編號。所有桿件材料密度均設為0.1 lb/in3(1 lb/in3=27 679.9 kg/cm3),彈性模量為10 000 ksi (1 ksi=6.84 MPa),桿件的應力約束為25 ksi,位移約束為2.0 in (1 in=25.4 mm)。外部荷載P施加在節點2和節點4上,大小為100 kips (1 kips=4.448 kN)。將10個桿件的橫截面積作為設計變量,將結構總體質量作為目標函數。優化變量從數據集S中選用,其中S=[0.1,0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0,5.5,6.0,6.5,7.0,7.5,8.0,8.5,9.0,9.5,10.0,10.5,11.0,11.5,12.0,12.5,13.0,13.5,14.0,14.5,15.0,15.5,16.0,16.5,17.0,17.5,18.0,18.5,19.0,19.5,20.0,20.5,21.0,21.5,22.0,22.5,23.0,23.5,24.0,24.5,25.0,25.5,26.0,26.5,27.0,27.5,28.0,28.5,29.0,29.5,30.0,30.5,31.0,31.5]in2,共有64種截面尺寸可供選擇。

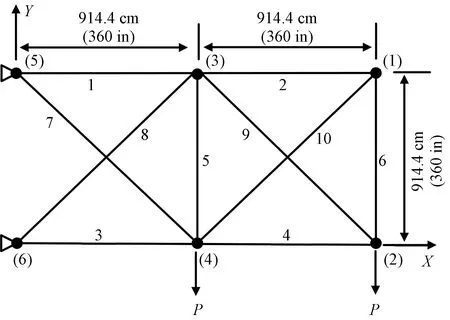
圖6 10桿平面桁架結構

十桿平面桁架結構優化設計問題已被眾多學者用于測試算法的尋優性能。歸納粒子群優化算法(particle swarm optimization,PSO)、含被動聚集因子的粒子群優化算法(particle swarm optimizer with passive congregation,PSOPC)、啟發式的粒子群優化算法(heuristic particle swarm optimization,HPSO)和螢火蟲算法(firefly algorithm,FA)的優化結果,并與AO和IAO的計算結果進行對比。設定AO和IAO的種群規模為50,總迭代次數為1 000,運行30次。優化結果如表3所示;迭代收斂曲線如圖7所示。

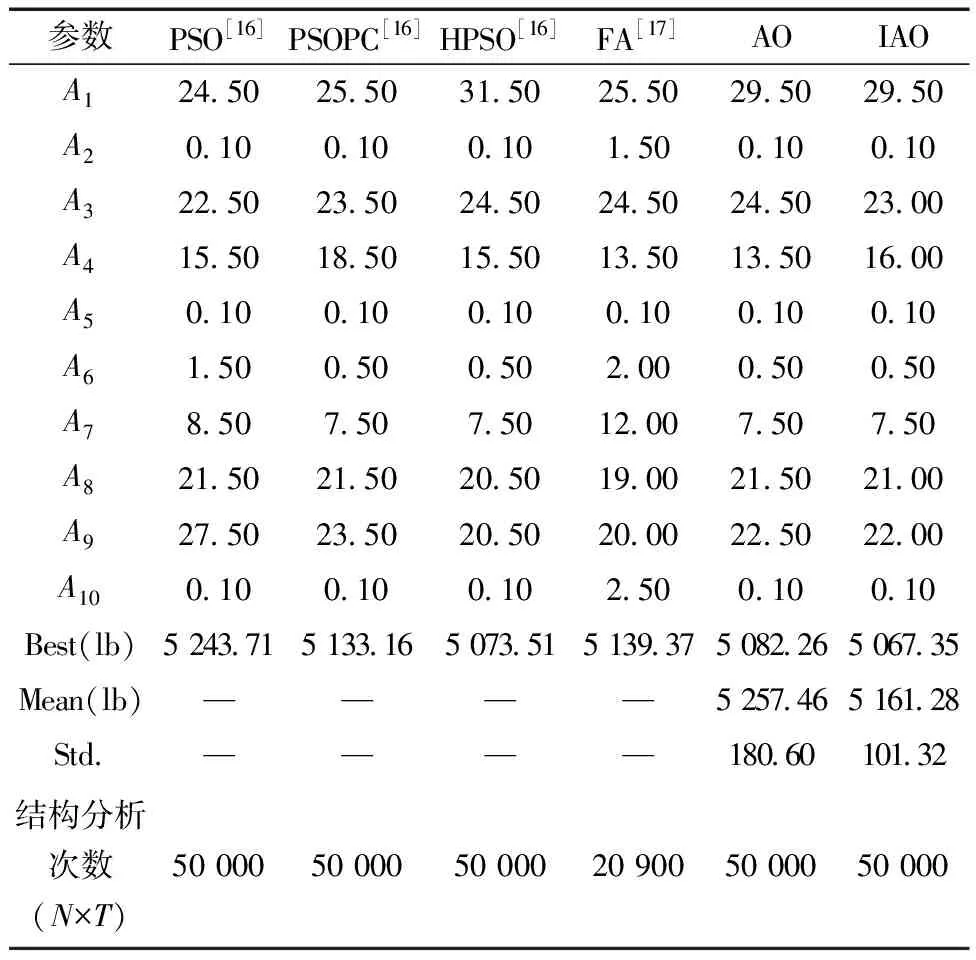
表3 十桿平面桁架優化結果對比

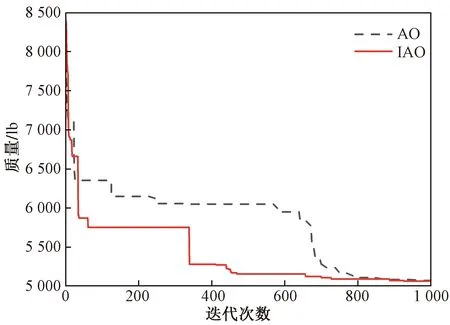
圖7 十桿平面桁架結構優化收斂曲線

由表3可知,IAO優化結果是最佳設計方案,總質量為5 067.35 lb,表明IAO具有較高的尋優精度;在AO和IAO獨立運行30次,結構分析次數統一為50 000次的情況下,IAO獲得的十桿桁架結構質量平均值為5 161.28 lb,標準差為101.32,均比AO的計算結果小,表明改進后算法在求解穩定性方面得到了提升。為了驗證IAO獲得的最優解是否可行,將IAO提供的最優解代入約束函數中檢查,此時節點最大位移為50.79 mm,沒有違反設定的位移約束條件;桿件最大應力為169.80 MPa,沒有違反設定的應力約束條件,因此IAO提供的設計方案是可行的。

圖7所示為IAO在迭代前期的收斂速度要高于AO,表明混沌映射初始化種群有利于算法在設計域內快速尋優;AO在迭代至800次時陷入局部最優,反觀IAO能夠不斷地跳出局部最優值,這是由于加入了反向學習策略和新的平衡搜索策略,使得IAO在迭代中期就可以進行局部搜索,在迭代后期也可以在設計空間進行全局尋優,提升了算法脫離局部最優值的能力。

4 抱桿結構的優化

4.1 抱桿優化模型

在有限元方法的基礎上,使用IAO對抱桿結構進行優化,在滿足結構承載力的情況下,尋找抱桿各部分所用角鋼的最合理尺寸。以結構的強度、剛度和穩定性為約束條件;以抱桿結構各部分所用角鋼主材和輔材的截面尺寸為優化變量;以抱桿整體的質量最小化為目標構建優化模型。

將抱桿結構質量記為W(x),結合罰函數法,可將優化設計的目標函數記為

(20)

式(20)中:k為約束個數;g(x)為約束函數;C為懲罰系數,當滿足約束時,C=0。

以結構的強度、剛度和穩定性為約束條件為

(21)

式(21)中:σzmax為主材最大應力;[σz]為主材許用應力;σfmax為輔材最大應力;[σf]為輔材許用應力;δmax為抱桿頂部水平最大位移;[δ]為規范允許的最大位移;μ為屈曲系數;[μ]為最小允許屈曲系數。規范規定搖臂抱桿的屈服強度安全系數和穩定安全系數不小于2.0;主桿體有懸臂結構的抱桿,桿體頂部的水平位移不得超過1.34H/100(H為抱桿的自由高度,等于抱桿自由段高與桅桿高度之和)。所以抱桿主材的許用應力[σz]=172.5 MPa,輔材的許用應力[σf]=117.5 MPa;最大允許位移[δ]經計算為348.4 mm;穩定安全系數即最小允許屈曲系數[μ]=2。

4.2 抱桿結構的優化計算

根據《熱軋等邊角鋼截面特性表》,選取邊寬范圍為40～110 mm的等邊角鋼建立截面庫。以抱桿主要四個部位的主材和輔材的角鋼型號為優化變量,共8個離散變量。變量從截面庫中選用,截面庫如表4所示。x1,x2,…,x8分別代表抱桿普通段主材和輔材,加強段主材和輔材,桅桿主材和輔材以及搖臂主材和輔材。

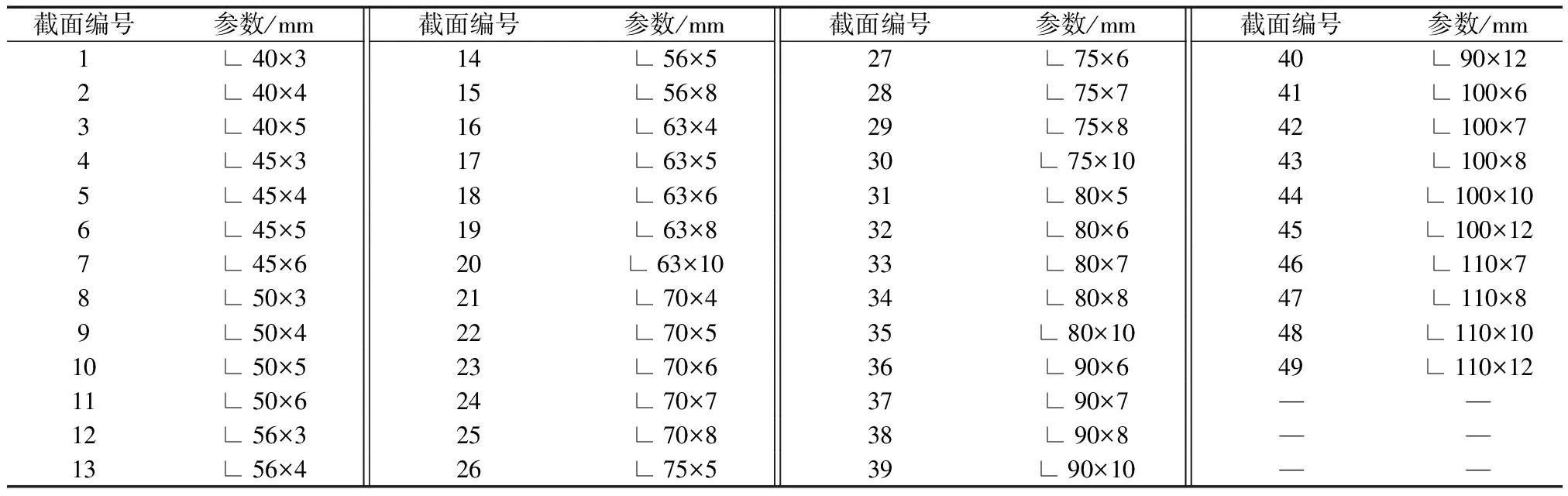
表4 抱桿截面型號庫

4.3 優化結果

統一設定算法的總迭代次數T=100,種群數為10,針對此危險工況進行優化。表5給出了蝴蝶優化算法(butterfly optimization algorithm,BOA)、鯨魚優化算法(whale optimization algorithm,WOA)、灰狼優化算法(grey wolf optimizer,GWO)、AO和IAO的優化設計結果。如表5所示,相比于其他算法,IAO找到了結果中抱桿的最佳設計方案,優化后質量為14.248 8 t,并且優化得到的抱桿均滿足穩定安全系數即屈曲系數不小于2.0。如表6所示,相比于原始設計方案,IAO優化后抱桿質量減輕了16.55%。

表5 5種算法的優化結果

表6 抱桿優化前后結果對比

圖8所示為5種算法對抱桿優化后對應的最大Mises應力云圖。BOA和WOA優化后的抱桿最大Mises應力均發生在桿身加強段頂部主材,分別為163.67 MPa和144.48 MPa。GWO、AO和IAO優化后的抱桿最大Mises應力均發生在桿身普通段和加強段交界處主材,分別為160.19、160.42和167.84 MPa。優化后得到的五種抱桿均滿足規范規定的2倍屈服強度系數。如圖9所示,優化后的5種抱桿頂部水平位移均未超過348.4 mm,均滿足規范規定的剛度要求。

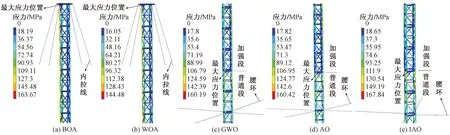
圖8 抱桿最大Mises應力云圖

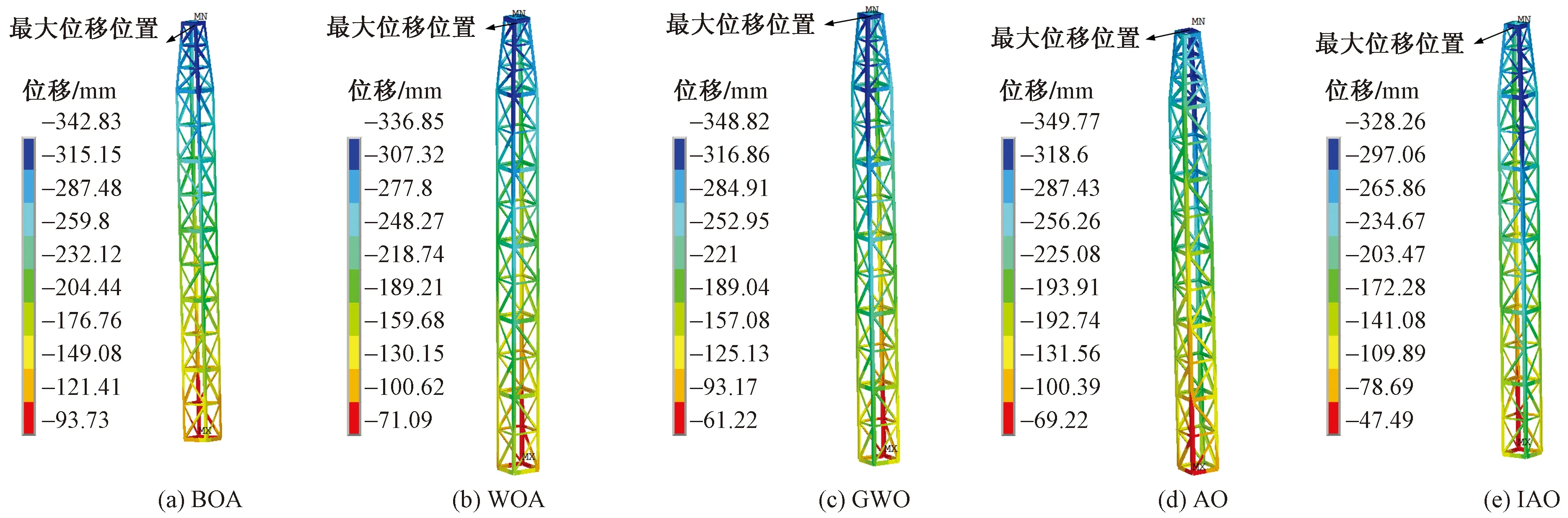
圖9 抱桿頂部最大水平位移云圖

圖10為5種算法的迭代收斂曲線,AO在迭代20次時陷入局部最優,而IAO能夠多次跳出局部最優值直至算法迭代終止,并且最終獲得抱桿的最小質量。因此,IAO具有最佳的尋優性能。

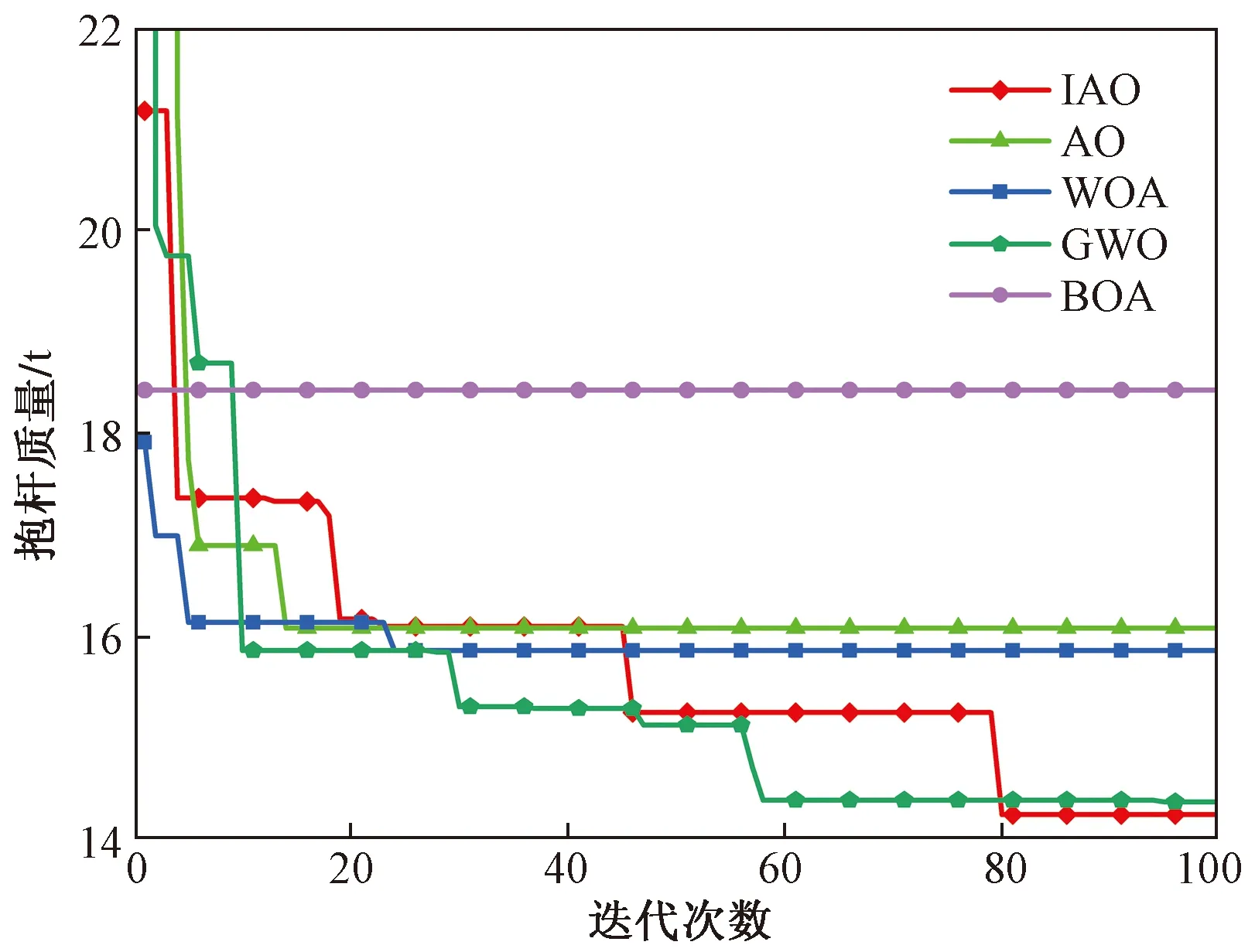
圖10 算法迭代曲線

5 結論

本文提出了一種改進的天鷹優化器,結合有限元方法和罰函數法,以結構的質量最小化為優化目標,對十桿平面桁架和抱桿結構進行優化設計。得到如下主要結論。

(1)IAO在AO中引入混沌映射、反向學習策略、非線性參數和新的平衡方式,算法的計算精度和脫離局部最優的能力得到了有效提高。

(2)IAO得到了十桿平面桁架結構的最佳設計方案。IAO在尋優精度和求解穩定性方面強于AO等算法,表明算法改進策略的有效性。

(3)IAO得到了抱桿輕量化設計最佳方案,各部分所用角鋼型號更加合理,抱桿結構在強度、剛度和穩定性方面均滿足規范要求,抱桿整體質量由17.074 2 t降為14.248 8 t,降幅為16.55%。

(4)IAO能夠有效地處理平面桁架和空間桿系結構的工程優化問題。