Analytical three-periodic solutions of Korteweg–de Vries-type equations

Mi Chen(陳覓) and Zhen Wang(王振)

1School of Mathematical Science,Dalian University of Technology,Dalian 116024,China

2School of Mathematical Science,Beihang University,Beijing 100191,China

Keywords: Hirota bilinear method,Riemann theta function,three-periodic solution

1.Introduction

There are many methods to study analytical solutions of nonlinear partial differential equations (NLPDEs), such as inverse scattering transform,[1,2]Painlevé analysis,[3,4]Darboux transformation,[5–9]deep learning method,[10]Hirota bilinear method, and so on,[11–15]among which Hirota bilinear method is an important method to obtain the exact solution of NLPDEs.In particular,Hirota bilinear method is extended to construct periodic solutions of some NLPDEs.

The periodic solution of NLPDEs is one of the hot topics in soliton theory.The quasi-periodic solutions is first studied by Dubrovin, Matveevet, Novikovet al., and they can also be called finite gap solutions.[16–18]Nakamura proposed a method of constructing quasi-periodic solutions based on Hirota bilinear method[19,20]and this method can be sued to obtain the algebraic relations among frequencies, phase shifts, amplitudes, and wave numbers.The existence condition forN-periodic solution of partial differential equations has been given, and whenN ≥3, this existence condition is an over-determined system.A few decades later, the two-periodic solutions of the Toda lattice equation, Nizhnik–Novikov–Veselov equation, the Fokas equation, the nonlocal Boussinesq equation, and KdV equation are obtained.[21–25]Recently,some three-periodic solutions of NLPDEs have been proved to exist, such as KdV-type equations and Tzitzeica equation,[26,27]but no one has yet given analytical expressions of their three-periodic solutions.We will construct the threeperiodic solutions of two KdV-type equations in this article.

We called KdV-type equations when the equation

can be transformed into bilinear form

by dependent variable transformation

whereFis an even function ofDt,Dx,..., andCis an integration constant.The standard identities for the HirotaDoperators:

The three-periodic solutions of the KdV and the Hietarinta equations, have been shown to exist, and their bilinear equations are as follows:[27]

In this paper,we construct the three-periodic solutions of the KdV and the Hietarinta equations and analyze the asymptotic relations between the periodic solutions and the soliton solutions.In addition,we also analyze the interactions of the three-periodic solutions.In Section 2, 8 algebraic equations satisfying the three-periodic solutions of the Hietarinta and the KdV equations are respectively obtained based on Riemann theta function and Hirota bilinear method.In Section 3, we construct the three-periodic solution of KdV equation,and the asymptotic relationship between the three-periodic solution and the three soliton solution is constructed.In Section 4,the three-periodic solution of Hietarinta equation and its asymptotic three soliton are constructed, then we find the periodic solutions and their asymptotic solitons can exhibit the same characteristic during the nonlinear interaction, namely, repulsive phenomenon.In Section 5,a summary is given.

2.The three-periodic solutions of KdV-type equations

2.1.Condition for N-periodic solutions

Based on the following multi-periodic Riemann theta function in genusN,we consider the multi-periodic solutions of the KdV and the Hietarinta equations:

with

τis a positive definite real valued symmetricN×Nmatrix.When we substitute Eq.(3)into Eq.(1)or Eq.(2),we can get

where

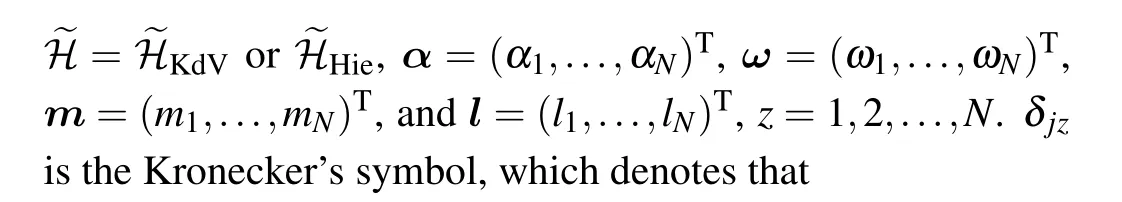
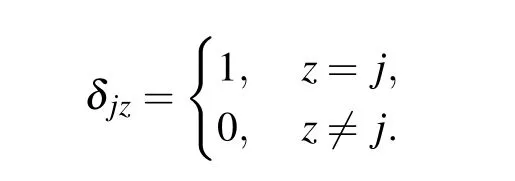
From Eq.(5)we can obtain

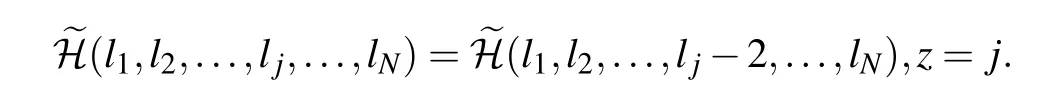
By inductive analysis,we can get From Eq.(6), whenn=Nwe have has 2Nequations.The wave numbers(α1,α2,...,αN)and the amplitude parameters(τ11,τ22,...,τNN) of the Riemann theta function of genusNare taken as arbitrarily given parameters, then the number of unknown parameters(ω1,ω2,...,ωN),τij(1≤i,j ≤N,i/=j),andCis (N2+N+2)/2.So whenN ≥3, equation (6) is an over determined system.

2.2.The three-periodic wave solutions of KdV-type equations

Based on Eq.(3),the three-periodic solution of the KdV equation or the Hietarinta equation is

with

τis a positive-definite real valued symmetric 3×3 matrix,which we name the periodic matrix of the Riemann theta function.The three-periodic solution exhibits the interaction of three periodic waves.τiirepresents the amplitude of thei-th wave,andτij(i/=j)represents the phase shift of the interaction between thei-th wave and thej-th wave.Based on Eq.(6),we can obtain 8 equations,

3.KdV equation

3.1.The three-periodic solution of KdV equation

In order to make the Riemann?3function(8)satisfy the bilinear Eq.(1),that is,

the following 8 equations are obtained

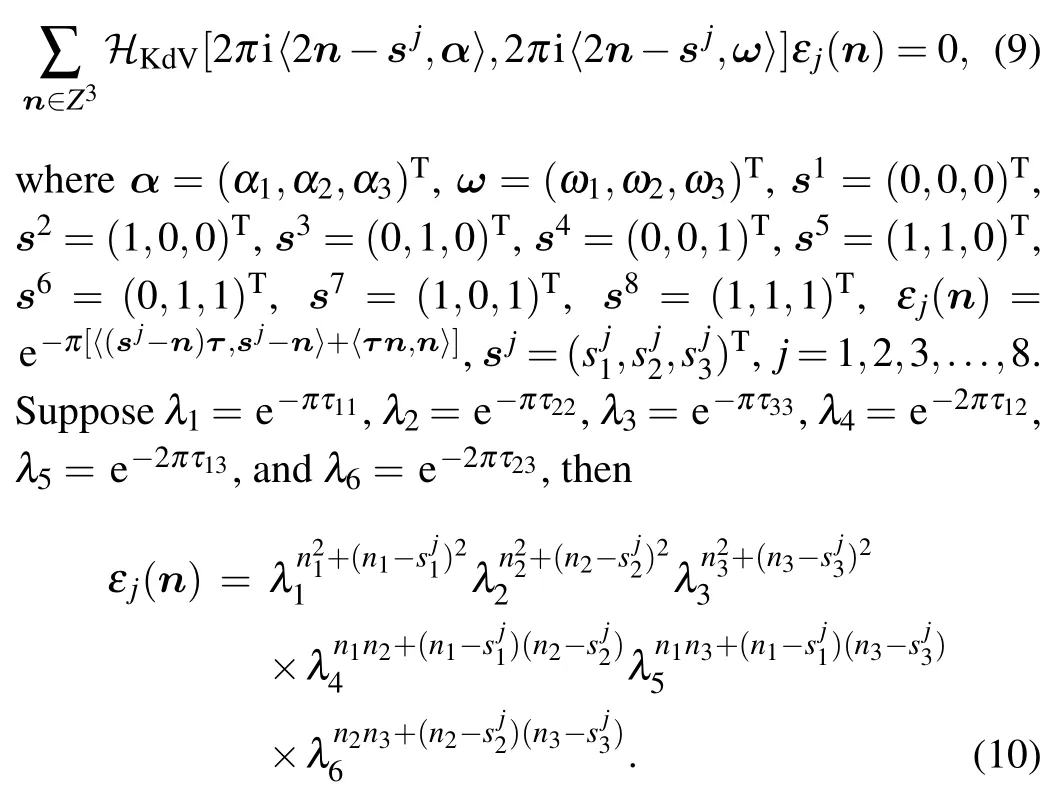
λ1,λ2,andλ3,can be regarded as small parameters,and then we denoteωi,Cas the series ofλ1,λ2,andλ3,

By substitute Eqs.(10)and(11)into Eq.(9),and the nonlinear equations can be transformed into linear equations.Then we collect all the coefficients ofλi1λ j2λk3in the linear equations and set the coefficients to zero one by one,then we can obtain some coefficient equations aboutωa,i,j,k,Ci,j,k,λ4,λ5,andλ6,(a=1,2,3),(i,j,k=0,1,2,...).By solving these coefficient equations,we can obtain the following results:

Substituting Eq.(12) into Eq.(7), the three-periodic solution of the KdV equation is obtained.

3.2.The asymptotic soliton of the periodic solution

WhenC=0 in Eq.(1),the three-soliton solution of KdV equation can be obtained[28]

with

If we denote

We choose appropriate parameters to ensure that the three waves of the three-periodic solution have the same velocity direction.We find that during the interaction, the asymptotic three-soliton solution presents the same repulsive phenomenon as the three-periodic solution.The interactions of the three-periodic solution and its asymptotic three-soliton soulition are shown in Figs.1(a) and 1(b) respectively.As can be seen from Fig.1,When the three branches of the threeperiodic solution approach to each other,the tall branch jumps forward and the other low branches jump back,forming a repulsion phenomenon.The three branches of the asymptotic three-soliton solution also present repulsion phenomenon during the interaction.

Fig.1.Choosing α1=0.01,α2=0.02,α3=0.03,C=0.1,and =0.(a)The three-periodic soulition with parameters τ1,1=0.6,τ2,2=0.7,τ3,3=0.8.(b)The three-periodic solution in panel(a)degenerates into the three-soliton solution with τii →+∞(i=1,2,3).(c)The three-periodic soulition of the KdV equation with parameters τ1,1 =0.6, τ2,2 =17, τ3,3 =0.8.(d) The three-periodic soulition of the KdV equation with parameters τ1,1=16,τ2,2=17,τ3,3=0.8.

The three-periodic solution degenerates to the twoperiodic solution when any one ofτ11,τ22, andτ33is large enough, and the one-periodic solution when any two of them are large enough.Next,we give two examples.Ifτ22is large enough,that isλ2?λ1,λ3,then equation(15)has the following form:

So equation(17)is the Riemann theta function of genusN=2,and the approximate two-periodic solution of KdV equation can be obtained by Eqs.(7)and(17)(see Fig.1(c)).Whenτ11andτ33are large enough,that isλ1,λ3?λ2,

Similarly,we can obtain an approximate one-periodic solution of the KdV equation from Eqs.(7)and(18)(see Fig.1(d)).

4.Hietarinta equation

4.1.The three-periodic solution of Hietarinta equation

In order to make the Riemann?3function(8)satisfy the bilinear equation(2),that is,

the following 8 equations are obtained

and then the unknown parameters are expressed as follows:

Equations (22)–(24) show the algebraic relationships among the free constantb, frequencies and wave numbers.It can be seen from the expression that the frequencyωjnot only is related to thej-th wave number but also to the other two wave numbers, in other words, the dispersion relationship of the waves has changed.By substituting Eq.(24)into Eq.(8),the three-periodic solution of Hietarinta equation is obtained.

The three-periodic solution is shown in Fig.2,and it has the following two characteristics: (i)The three-periodic solution is symmetric about thexandtaxes (see Figs.2(c) and 2(d)).(ii) It has 2Nfundamental periods{ζi,i=1,2,...,N}and{τi,i=1,2,...,N}in(ξ1,ξ2,ξ3)withζ1=(1,0,...,0)T,...,ζN=(0,0,...,1)T.

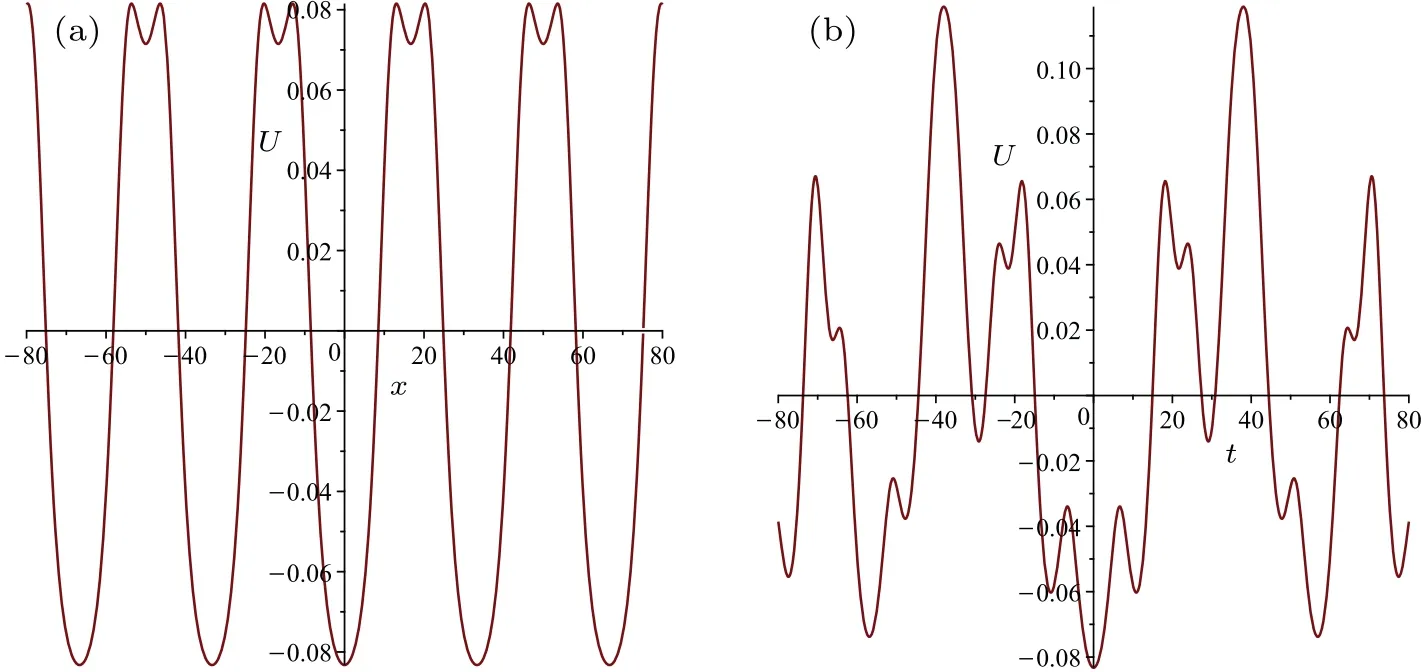
Fig.2.The three-periodic solution of the Hietarinta equation with parameters α1 =0.03, α2 =0.06, α3 =0.09, τ1,1 =0.85, τ2,2 =1.05,τ3,3=1.25,λ1=0.06922773125,λ2=0.03693217019,λ3=0.01970287297,C=0.1,and =0.(a)The three-periodic solution of the Hietarinta equation at t=0.(b)The three-periodic solution of the Hietarinta equation at x=0.

4.2.The asymptotic soliton of the periodic solution

WhenC=0 in the bilinear equation (2), the three soliton solution of Hietarinta equation can be obtained by using Hirota bilinear method

with

If we denote

then

Supposeθi=ιix+νit+andC= 0 then equation (27)changes into

atλ1= e-πτ11,λ2= e-πτ22,λ3= e-πτ33→0.Therefore,the equation (28) shows that the three-periodic solution (27)of Hietarinta equation can be reduced to its three-soliton solution(26).

It can be seen from Fig.3(a) that the three branches of the three-periodic solution of the Hietrinta equation,and they move in the same direction.The three-periodic solution of Hietrinta equation degenerates into its three-soliton solution asλ1,λ2,λ3,→0 (see Fig.3(b)).Similar to the periodic and soliton solutions of the KdV equation, it can be seen from Figs.3(a)and 3(b)that when the three branches of the threeperiodic solution or the three-soltion solution of the Hietrinta equation approach to each other, the high beanch jumps forward and the other low branches jump backward, forming a repulsive phenomenon.As can be seen from Figs.3(a), 3(c),and 3(d), when any two or one ofτ11,τ22, andτ33are large enough,the three-periodic soulition can degenerate to two-or one-periodic soulitions.

5.Conclusion

We gave the approximate analytical three-periodic solutions of the KdV equation and the Hietarinta equation for the first time by using the perturbation method.We obtained the algebraic relations among phase shift,wave numbers,frequency, and amplitudes after tedious calculations.By a limit method, that is,τ1,1,τ2,2,τ3,3→+∞, the three-periodic solutions of the KdV equation and the Hietarinta equation degenerate into three-soliton solutions.We find that the threeperiodic solution presents the same repulsive phenomenon as the asymptotic three-soliton solution during the interaction.Moreover, we find that when one or two ofτ1,1,τ2,2,τ3,3are large enough, the three-periodic solution can degenerate into the one-or two-periodic solution.

Acknowledgements

Project supported by the National National Science Foundation of China (Grant Nos.52171251, U2106225, and 52231011) and the Science and Technology Innovation Fund of Dalian City(Grant No.2022JJ12GX036).