基于干擾觀測器的機械臂廣義模型預測軌跡跟蹤控制

盧紫超, 李 通, 孫澤文, 田 霖, 孫 亮, 劉冀偉

(1.北京科技大學 智能科學與技術學院,北京 100083; 2.中華人民共和國民政部一零一研究所,北京 100070;3.北京科技大學 自動化學院,北京 100083)

機械臂是高精度、多輸入多輸出、高度非線性、強耦合的復雜系統。因其獨特的操作靈活性,已在工業裝配、安全防爆等領域得到廣泛應用。機械臂的非線性控制穩態精度和抗干擾能力一直是研究領域的重點問題。

在許多控制系統的設計過程中,常常會面臨實際對象與數學建模得到的模型之間存在差異的問題,這是因為在建模過程中存在參數不確定性以及外界的未知干擾[1-4]。

廣義預測控制(Generalized Predictive Control,GPC)算法是通過在線辨識獲得模型參數,并利用模型參數實現多步預測和滾動優化,同時又具有自適應特征的控制算法。因此GPC對于建模誤差等未知因素具有較好的適應能力。但是一些含有較大建模誤差和較大外界干擾的復雜控制系統,會出現預測輸出和實際輸出相差較大的情況,無法得到滿意的控制效果[5-9]。文獻[10]將改進的比例性能指標型廣義預測控制器引入多變量系統中,通過預測增量表征系統變化趨勢,并通過控制量進行補償優化控制性能。文獻[11]提出了一種求解廣義預測控制律的快速算法,解決了計算量較大的問題。文獻[12]提出了一種模糊廣義預測控制的方法,并將其應用到了連續攪拌反應釜系統中。

干擾狀態觀測器通過獨立于數學模型的特殊反饋機制可以很好地跟蹤參數不確定性和外界干擾,并成功應用于各種對象[13]。利用干擾觀測器觀測系統存在的不確定性成為了一種克服這些不確定性的有效算法[9]。將干擾觀測器應用于GPC中,通過估計模型不確定性以及外界的干擾來提高系統的魯棒性能。文獻[14]提出了一種基于狀態觀測器的四旋翼反步輸出反饋軌跡跟蹤控制器,分數階反饋的狀態觀測器可以提高控制器的跟蹤性能和自適應性。文獻[15]提出了基于狀態觀測器的有限時間控制器,解決了非仿射非線性系統的執行器故障問題。文獻[16]針對剛性航天器的容錯問題,設計了一種基于干擾觀測器的自適應魯棒控制器。文獻[17]提出了一種基于擴張狀態觀測器和反步法的四旋翼飛行器姿態控制器,通過干擾觀測器觀測四旋翼飛行器收到的擾動,提高了系統的魯棒性能。

本文將廣義模型預測方法應用于機械臂軌跡跟蹤控制器的設計之中,優化控制系統的性能。針對機械臂軌跡跟蹤運動學子系統,采用GPC方法設計期望的虛擬關節角速度。對于機械臂軌跡跟蹤動力學子系統,考慮機械臂的參數不確定性和未知外界擾動,利用廣義預測控制方法設計關節力矩控制輸入。從工程實際角度出發,考慮到機械臂運動的匹配和不匹配模型不確定性的影響以及機械臂在實際運行環境中外界的未知干擾,GPC可以通過多步預測和滾動優化對建模誤差和未知因素產生較好的適應能力,本文基于非線性干擾觀測器方法設計魯棒控制項,保證系統的魯棒性。基于上述設計思想,本文針對受外部干擾和參數不確定性影響的多輸入多輸出耦合機械臂系統動力學模型,提出了一種具有非線性干擾實時在線補償的GPC方法。在控制設計中,針對關節角度子系統和關節角速度子系統的級聯性,分層設計了基于非線性干擾觀測器的廣義模型預測運動學控制器和動力學控制器。所提出的控制方法可以為機械臂控制器提供一種通過預測時長整定控制器反饋增益的調參方法,整定后的參數可保證受控系統的誤差軌跡和控制輸入具有一定優化性能。通過數值仿真驗證了閉環系統的穩定性和有效性。

1 問題描述

考慮n自由度機械臂的動力學模型如下:

(1)

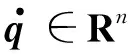
若考慮機械臂模型的參數不確定性及外部干擾影響,將機械臂動力學模型(1)降階為2個級聯的子系統,第1個子系統描述關節角位置動態:

(2)

第2個子系統描述關節角速度動態:

(3)

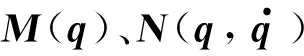
假設外部干擾信號f1、f2及其各階導數均有界且期望關節運動軌跡qr(t)本身及其各階時間導數均有界。

本文控制目標是考慮模型(2)和模型(3)中的外部不匹配干擾f1和聚合干擾f2的影響,設計控制輸入力矩u使得機械臂關節軌跡q(t)跟蹤上期望軌跡qr(t),并使得軌跡跟蹤誤差最終收斂到原點小鄰域。

2 關節角位置跟蹤控制器設計

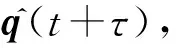
(4)

取最小值。該性能指標函數對關節角位置和角速度跟蹤信號進行了優化,保證系統動態跟蹤性能。

由泰勒展開公式可得在t+τ時刻關節角位置q(t+τ)及其一階導數的預測值可近似寫為

(5)

(6)

(7)

(8)

由以上各式可將指標函數J1近似化成如下形式:

(9)

式中:A為3n×3n的常值對稱矩陣。

(10)

(11)

(12)

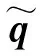
(13)

(14)

則y-yr可以表示為

(15)

則由式(9)有:

(16)

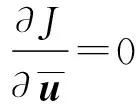
(17)

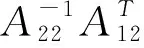
(18)

由Kp的定義可知:

(19)

則Kp為正對角陣。將式(13)和式(14)代入式(18)可得:

(20)

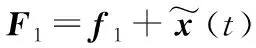
(21)

式中:z1為觀測器狀態;Lp為觀測器的增益矩陣。可以設計實際的角速度虛擬控制律為

(22)

由式(19)可知,增益矩陣Kp的取值取決于預測時長T1。在實際的機械臂應用中,預測時長表示對未來狀態的預測程度。當預測時長T1較大時,可以對關節角位置有較長的預測,但是會產生較大的誤差,會降低軌跡跟蹤的精度;當預測時長T1較小時,無法使式(4)中的滾動優化性能指標達到最優值。故在實際應用中選擇一個合適的預測時長,使控制器可以根據當前誤差及時修正系統的輸入信號。觀測器增益矩陣LP也需要根據實際應用對其進行調節,過大和過小都無法獲得較好的預測效果。

3 關節角速度跟蹤控制器設計

針對關節角速度子系統設計了實際關節力矩控制輸入,設定合適的控制力矩實現最優跟蹤。與關節角位置跟蹤設計類似,通過最小化以下指標函數實現:

(23)

類似虛擬控制器設計的推導過程,可設計使得式(23)最小的廣義預測控制器,得到控制力矩輸入為

(24)

類似Kp的推導過程,可以得出角速度控制系統中的Kd為

(25)

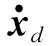
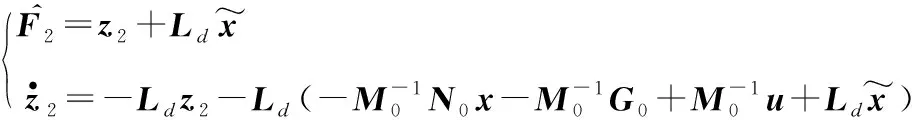
(26)

式中:z2為觀測器狀態;Ld為觀測器的增益矩陣。輸入的控制力矩可以重新設計為

(27)

式中:角速度控制系統中的Kd取決于預測時長T2和加權常數λ。Kd的取值過小會降低軌跡跟蹤的跟蹤精度,過大會產生較大的控制力矩。Ld參數的選取直接影響觀測器的預測效果。所以針對不同的應用對象需要根據實際情況進行調節以實現良好的控制性能。

4 穩定性分析

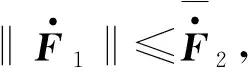
證明:定義觀測器的誤差為

(28)

(29)

由式(21)和式(26)可得出擾動觀測器的誤差為

(30)

(31)

定義李雅普諾夫函數:

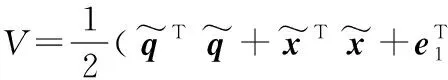
(32)

對李雅普諾夫函數求導得:

(33)

整理得:

=-ρV+c

(34)

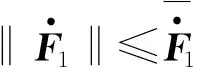
其中:

(35)

(36)

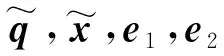
5 仿真算例

本文采用雙連桿剛性機械臂進行了數值仿真,驗證了所提出控制器的有效性。定義q=[q1,q2]T,x=[x1,x2]T分別為機械臂的關節角度和關節角速度。兩連桿剛體機器人數學模型中的相關矩陣如下[8]:

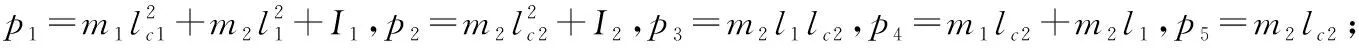
假設雙聯桿機械臂的初始角位置為q(0)=[0,0]T,采樣周期τ=0.01 s,預測時長T1=1.3 s,T2=1.7 s,關節角期望軌跡qr=[0.1sin(0.5t)+cos(0.5t),0.1sin(t)+cos(t)]T,擾動力矩f=[0.5sin(0.1t)+0.5,0.5(cos(0.1t))+0.5]TN·m,不匹配外部干擾f1=[0.1sin(0.1t),0.1sin(0.1t)] N·m,擾動觀測器的初始狀態z1(0)=z2(0)=[0,0]T,觀測器增益矩陣Lp=25E2,Ld=5En,M0中的標稱參數m10=1.5 kg,m20=0.5 kg,l10=0.34 m,l20=0.3 m。PD控制器中,比例系數kp=100E2,微分系數kd=10E2。經過數值仿真,實驗結果如圖1～圖3所示。

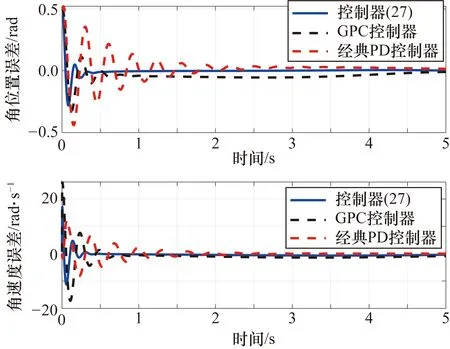
圖1 關節1的角位置和角速度跟蹤誤差

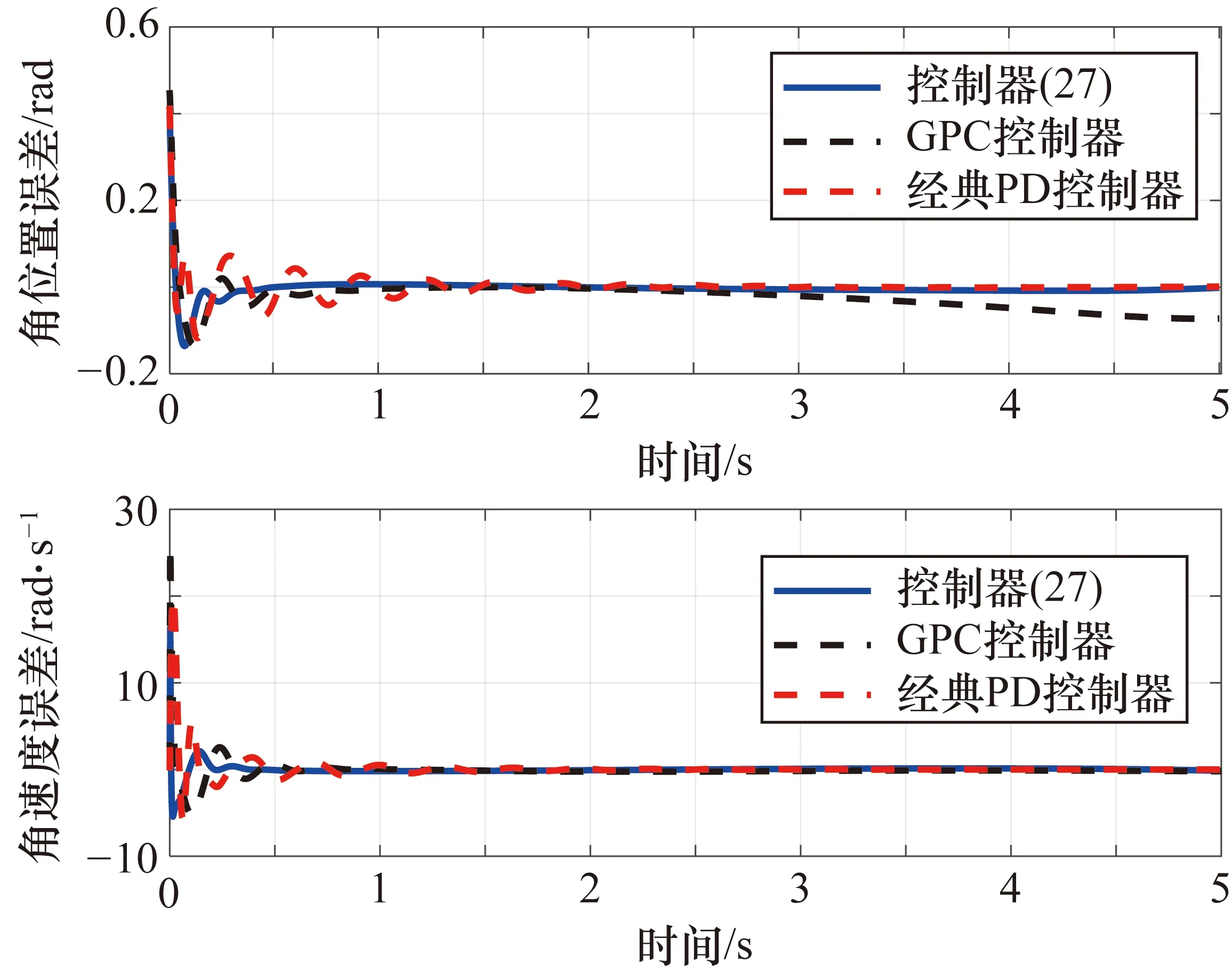
圖2 關節2的角位置和角速度跟蹤誤差

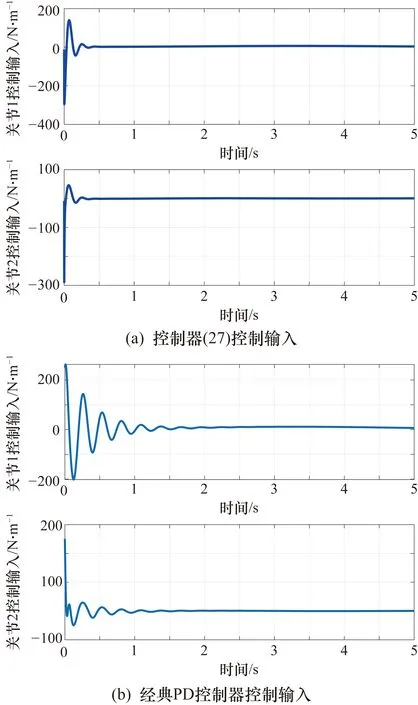
圖3 關節1和關節2的控制輸入

由圖1～圖3可以看出,在本文提出的控制器(27)的作用下,關節1和關節2的角位置跟蹤誤差在0.5 s時到達期望值附近,隨后實現穩定跟蹤。關節1和關節2的角速度跟蹤誤差在0.6 s收斂至零附近,并保持在零的領域中實現穩定跟蹤。在初始階段,為了實現較快的跟蹤,控制輸入在初始階段較大,在0.5 s后漸漸收斂至零附近。干擾觀測器的觀測值如圖4和圖5所示,最終收斂至零的鄰域。相對于經典的PD控制器,本文所提出的控制器在收斂時間和跟蹤精度方面均表現比較優異,在關節1中,明顯看出本文提出的控制器具有較小的超調。相對于經典的廣義預測控制器,加上干擾觀測器后,系統的收斂精度和收斂速度明顯優化。此外,通過絕對誤差積分準則(Integral Absolute Error,IAE)和時間乘絕對誤差積分準則(Integral of Time and Absolute Error,ITAE)對3種控制方法進行了對比,結果如表1所示,控制器(27)的控制效果明顯優于其他兩種控制方法。綜上所述,基于干擾觀測器的廣義模型預測控制器可以使角位置誤差和角速度誤差收斂至零的鄰域,實現較好的跟蹤效果。

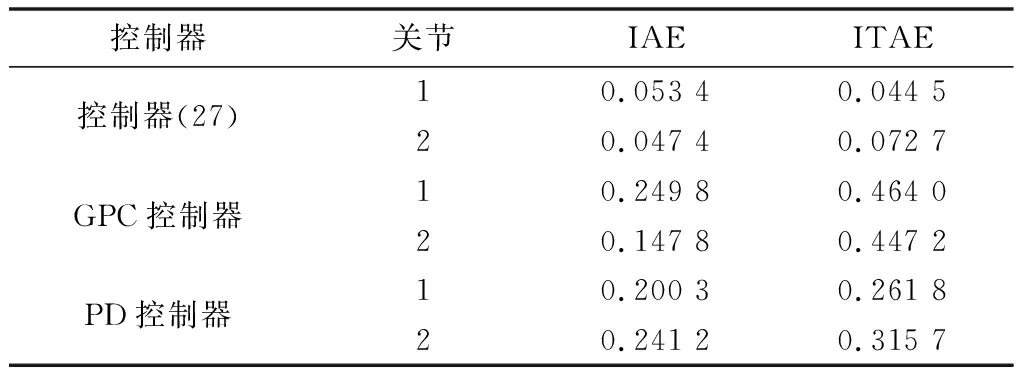
表1 3種控制器IAE、ITAE指標對比

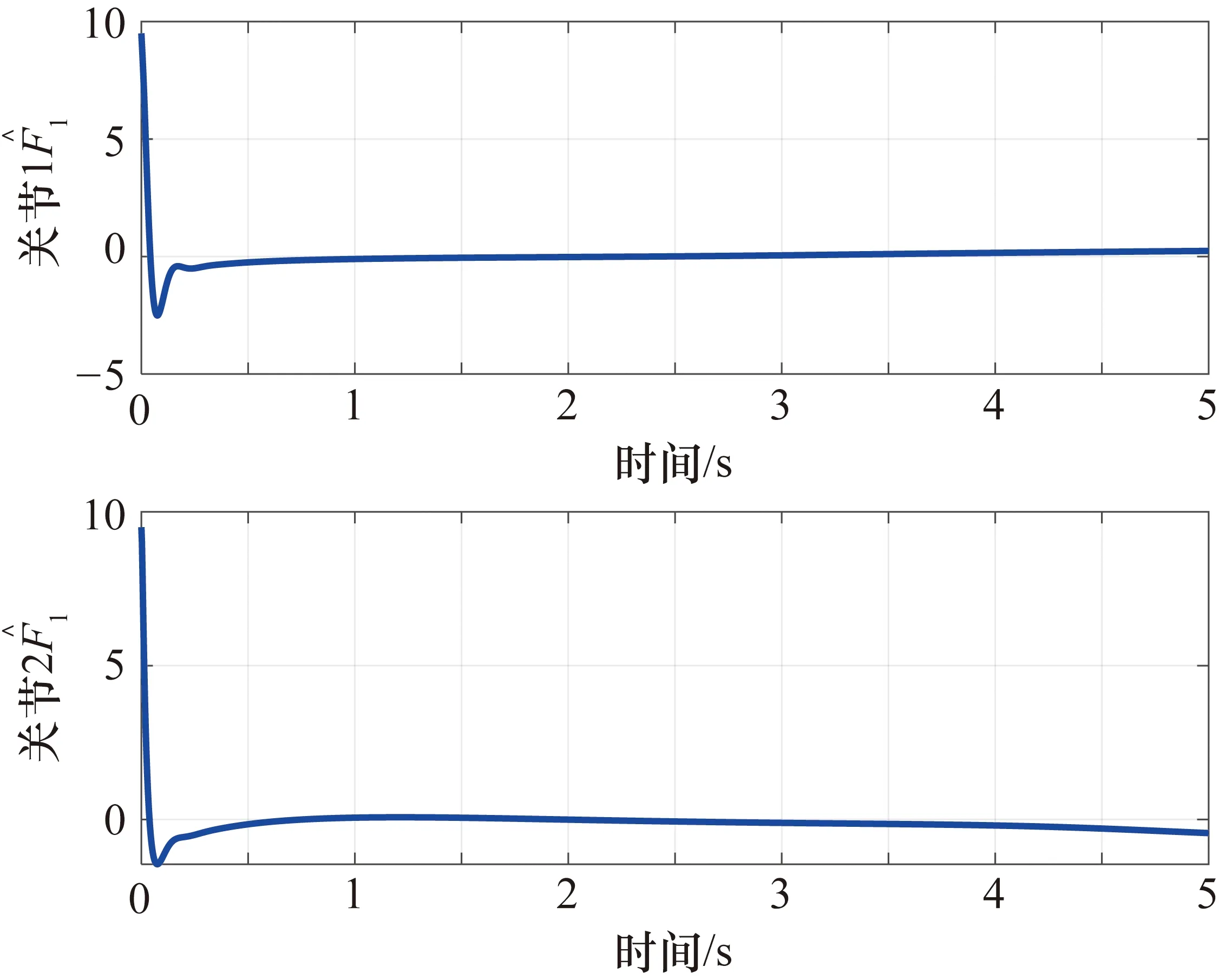
圖4 關節1和關節2的值

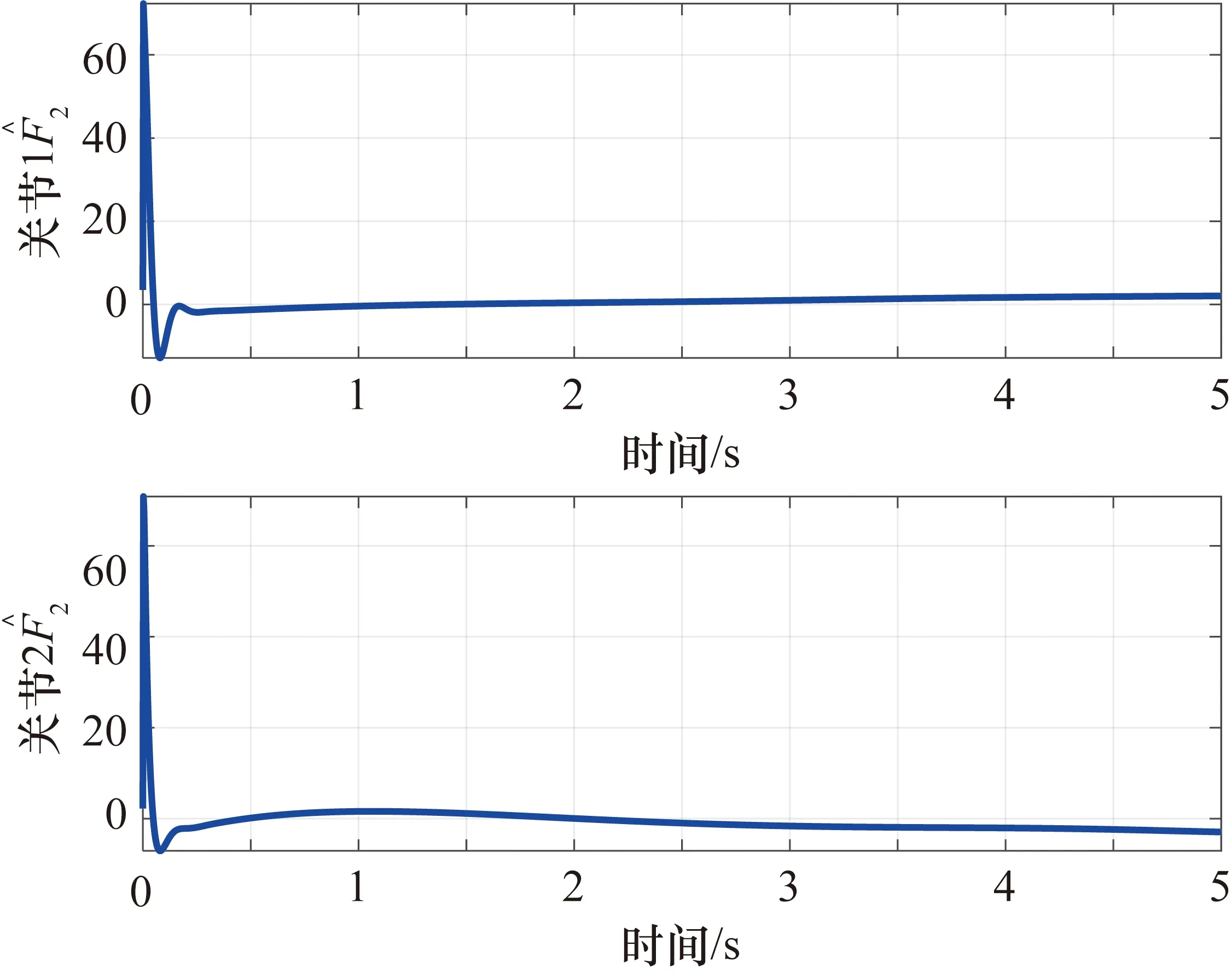
圖5 關節1和關節2的值

為了驗證本文所提出控制方案的魯棒性,在各種數字信號干擾和負載變化(復合干擾)情況下進行了仿真實驗。將外部干擾重新取為f=[C1sign(sin(0.4πt)),C2sign(sin(0.4πt))],其中C1分別取6、4、2;C2分別取3、2、1。在機械臂的末端執行器上添加變化負載m=1.25+sin(t)。仿真實驗結果如圖6～圖9所示。從圖6～圖9中可以看出,在復合干擾的作用下,當數字干擾信號到達時,關節1和關節2的角位置誤差和角速度誤差會產生波動,并且干擾的幅值越大,波動越大。在控制器(27)的作用下,在受到干擾后,角位置跟蹤誤差和角速度跟蹤誤差會收斂至零的鄰域,實現穩定的跟蹤效果。

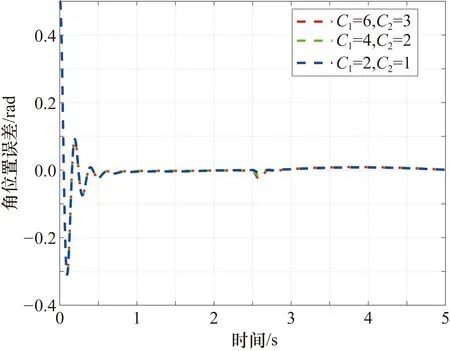
圖6 不同復合干擾下關節1的角位置跟蹤誤差

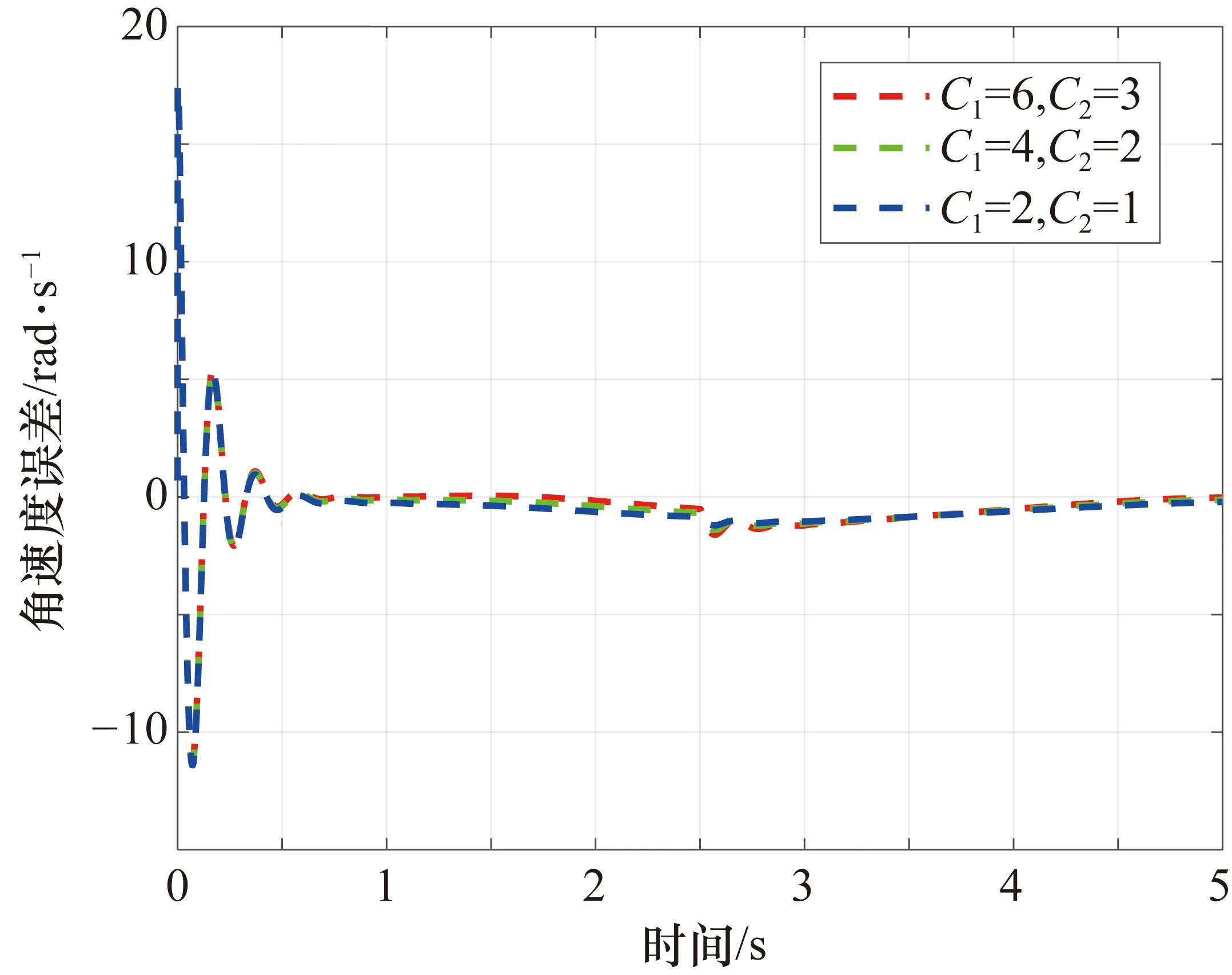
圖7 不同復合干擾下關節1的角速度跟蹤誤差

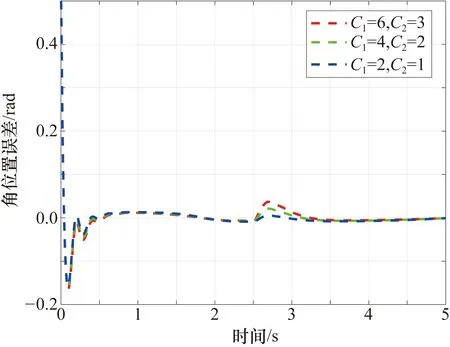
圖8 不同復合干擾下關節2的角位置跟蹤誤差

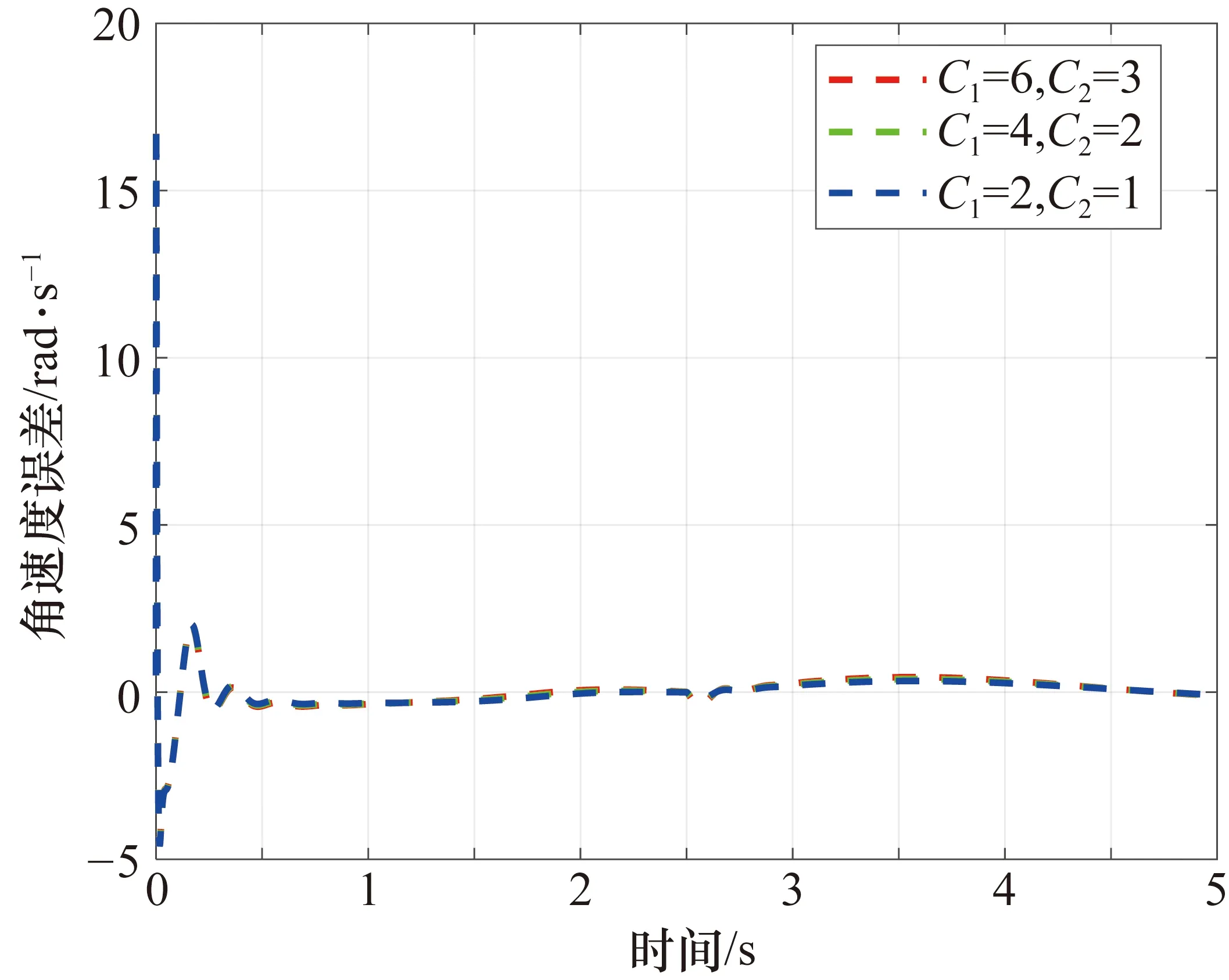
圖9 不同復合干擾下關節2的角速度跟蹤誤差

6 結束語

本文以兩連桿剛性機械臂為例,進行了基于干擾觀測器的廣義模型預測軌跡跟蹤控制研究。利用GPC的方法分別設計了期望的虛擬關節角速度和關節力矩控制輸入,利用非線性干擾觀測器的方法實時估計并補償系統模型中的不確定性。由于GPC可以通過多步預測滾動優化來適應實際的工作場景,并 通過干擾觀測器補償建模的不確定性和外界干擾,故通過調節合適的參數可使本算法應用于不同的實際工程。仿真結果表明,所提出的控制器可以使跟蹤誤差收斂至零的鄰域,實現很好的跟蹤效果。本文為了驗證所提出控制器的魯棒性,進行了數字信號干擾和負載變化共存情況下的仿真實驗,結果表明該控制器有較好的魯棒性。