基于不變擴展卡爾曼濾波的無人機姿態估計

李世強, 易文俊

(南京理工大學 瞬態物理國家重點實驗室,江蘇 南京 210094)

近年來,無人機迎來了大發展,被廣泛用于軍事偵察、安防巡檢、災后搜救、農業生產以及攝影航拍等不同領域,其中尤以四旋翼飛行器(以下簡稱“四旋翼”)最為流行。許多研究人員也對四旋翼產生了濃厚的興趣,搭建了多種飛行平臺,實驗了不同的控制算法。飛行器要實現穩定可靠飛行,必須準確高效地獲取自身的各種狀態信息。而四旋翼本質上是一個欠驅動系統,只能產生垂直于機體平面的升力,姿態估計信息被用于最底層控制環路以穩定飛行器,因此快速準確的姿態估計算法尤為重要,飛行控制算法的穩定性和可靠性直接依賴于姿態解算的精度和速度[1]。

由于受到成本、載荷和尺寸的限制,四旋翼普遍依賴慣性測量單元 (Inertial Measurement Unit,IMU)估算姿態。IMU是一組傳感器,由測量加速度的加速度計和測量角速度的陀螺儀組成,通常還包括一個磁力計來測量地球的磁場。這3個傳感器中的每一個都產生一個3軸測量值,總共構成一個9軸測量值。但IMU不提供直接的姿態估計,為了提高性能和魯棒性,必須對原始信號進行非線性濾波和數據融合處理,方能重建平滑的姿態估計和校正角速度測量的偏差。此外,從不同的傳感器測量結果中同時估計姿態和陀螺儀偏差大為有益[2]。

剛體姿態估計問題極具挑戰性,幾十年來一直是導航研究的焦點。這是因為剛體旋轉的基本位形空間,即特殊正交群SO(3)不是向量空間而是彎曲空間,所以姿態估計本質上是非線性問題[3]。簡單直接地用局部坐標(例如歐拉角、Rodrigues參數)來表示旋轉存在諸多問題。局部坐標包含需要進行特殊處理的奇異點(例如當俯仰角為90°時),并且估計既取決于局部坐標的選擇,也取決于固定和移動參考坐標系。如果將標準向量空間中的濾波方法不加改造地用到姿態的局部坐標表示上,則不僅狀態空間動力學方程和測量方程高度非線性,依賴于參考坐標的選擇,而且濾波性能在位形空間的不同區域高度不均勻[4]。

許多濾波方法都致力于處理非最小姿態表示所固有的約束。乘性擴展卡爾曼濾波器(Multiplicative Extended Kalman Filter,MEKF)因其靈活性和計算效率高而得到廣泛應用。它利用旋轉矩陣(或四元數)的幾何結構,對在原點處線性化的本征狀態誤差建立了誤差狀態卡爾曼濾波器。然而,當動態、測量模型高度非線性或沒有良好的先驗狀態估計時,MEKF容易出現發散現象[5]。

不變觀測器理論基于估計誤差在矩陣李群的作用下不變[6],該性質被稱為系統的對稱性[7],推動了不變擴展卡爾曼濾波(Invariant Entended Kalman Filter,InEKF)的發展[8-9],在即時定位與地圖構建(Simultaneous Localization and Mapping,SLAM)[10]和輔助慣性導航系統[11]中得到成功應用并取得良好效果。由InEKF算法可知,如果狀態定義在一個李群上,并且動力學方程滿足“群仿射”特性,那么對稱性使得估計誤差滿足李代數上的“對數線性”自治微分方程[8]。在確定性情況下,該線性系統可以用來精確地復原在群上演化的非線性系統的狀態估計。因此,對數線性特性允許設計一個非線性觀測器或具有強收斂特性的狀態估計器[12]。

在本文中,基于InEKF理論解決李群SO(3)上的姿態估計問題,建立連續時間運動模型和離散時間觀測模型。定義的確定性系統滿足“群仿射”特性,因此,誤差動態是對數線性的。在實踐中,隨著傳感器噪聲和IMU偏差的引入,該對數線性誤差系統只是近似成立,在許多情況下,由于優越的收斂性和一致性,InEKF仍然表現良好。可以通過MATLAB仿真實驗來證明所開發濾波方法的效用和準確性。

1 理論背景及預備知識

首先回顧一些有關特殊正交群SO(3)及其李代數so(3)的基本知識和有用的數學公式,這將在后面的章節中用于推導InEKF算法。

SO(3)中的元素由滿足RTR=I,det(R)=1的3×3實矩陣R組成,這里的I表示3×3單位矩陣。SO(3)是一個矩陣李群,與其相關聯的李代數記為so(3),是3×3斜對稱矩陣。為方便計算,令(·)∧表示R3到so(3)的線性映射。

(1)

so(3)和SO(3)之間由指數映射exp建立聯系:

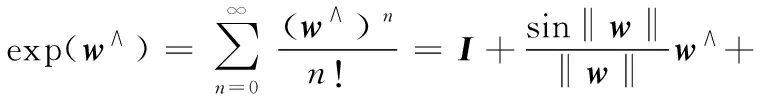
(2)

式中:‖·‖為標準向量范數。為方便,記Exp(w)=exp(w∧)。

對于任意R∈SO(3),w∧∈so(3),有伴隨映射Rw∧RT=(Rw)∧。另外,定義J為SO(3)的左雅可比,有

(3)

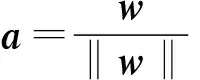
在SO(3)中運動的連續軌跡R(t)有

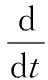
(4)

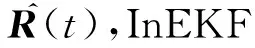
(5)

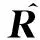
對fw(R)有

fw(R1R2)=R1R2w∧

=fw(R1)R2+R1fw(R2)-R1fw(I)R2

(6)

式(6)即為“群仿射”特性[8]。由于“群仿射”特性,右和左不變誤差是軌跡獨立的,即滿足

=0

(7)

=ηlw∧-w∧ηl

(8)

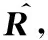
(9)

2 建立模型

在描述InEKF算法之前,首先需要建立坐標系,定義符號系統,建立四旋翼無人機姿態運動模型,描述傳感器測量模型及其基本假設。

2.1 參考坐標系

為了描述四旋翼無人機的姿態,以及討論加速度計和陀螺儀的測量值,必須引入一些參考坐標系。通常定義兩個坐標系表達姿態角的關系,一般使用導航坐標系(N系)和機體坐標系(B系)。導航坐標系,即當地的地理坐標系,相對大地水平面定義,坐標軸Xn,Yn,Zn分別指向地理上的北、東和當地垂線方向(向下),即北東地(NED)坐標系。機體坐標系則使用標準右前上坐標系,坐標軸Xb,Yb,Zb分別指向無人機的右側、前方以及上方。機體坐標系到導航坐標系的坐標變換矩陣用R表示,即無人機的姿態。

2.2 運動模型和測量模型

四旋翼無人機由旋轉矩陣表示的連續時間姿態運動方程為

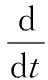
(10)

式中:Ω∈R3為無人機在機體系內的瞬時角速度,由陀螺儀測量。然而測量結果被加性高斯白噪聲過程干擾,即

(11)

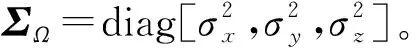
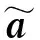
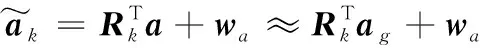
(12)

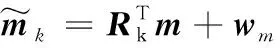
(13)

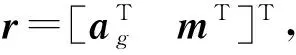
(14)

式中:Vk∈R6是由wa和wm組成的高斯噪聲。則有

(15)

3 不變擴展卡爾曼濾波

3.1 預測

考慮完整的系統運動方程和測量方程:

(16)

噪聲wΩ的引入,使得右不變誤差η變為

(17)

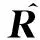
(18)

(19)

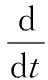
(20)

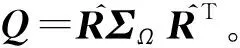
3.2 測量更新

為了將新的測量值納入考量,記zk∈R6為更新量,取為

(21)

狀態校正方程為

(22)

η+=Exp(Kkzk)η

(23)

式中:Kk為時刻tk的卡爾曼增益矩陣,同樣用η=Exp(ξ)≈I+ξ∧進行一階近似將式(23)線性化,忽略高階項,有

η+≈I+ξ+∧≈I+ξ∧+(Kkzk)∧

(24)

因此

ξ+=ξ+Kk((I-ξ∧)r-r+Vk)

=ξ+Kk(-ξ∧r+Vk)

=ξ+Kk(Hξ+Vk)

(25)

最后,可以利用導出的線性更新方程和卡爾曼濾波理論將InEKF的狀態和協方差更新方程寫成

(26)

式中:卡爾曼增益矩陣Kk由式(27)計算

(27)

由式(25)可得靈敏度矩陣H和測量噪聲協方差N為

(28)

3.3 引入陀螺儀偏差

在硬件上實現基于IMU的狀態估計算法通常需要對額外的狀態加以考慮,如陀螺儀和加速度計的偏差。可以使用兩種不同的方式來進行處理。一種是將偏差作為一個恒定的參數,假設它通常在比實驗時間更長的時間段內變化,然后可以在一個單獨的實驗中對偏差進行預校準。另一種是視偏差為所估計的狀態的一部分,則可以在估計姿態時同步估計偏差。本文采用后一種方式,因為在線實時補償偏差的影響能提高姿態估計的精度。但是,一旦將偏差納入考慮,則沒有李群可以滿足動力學方程的群仿射特性。盡管InEKF的許多理論性質不再成立,但仍能設計一個“增廣InEKF”,其性能仍然優于標準EKF[14]。由于兩種偏差的處理過程相似,為節省篇幅,本文只考慮陀螺儀偏差。

陀螺儀的偏差b是緩慢時變信號,以加性的方式破壞測量結果

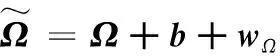
(29)

模型的狀態現在變為坐標變換矩陣R和偏差b,χ=(R,b)∈SO(3)×R3。現在定義增廣的右不變量誤差為

(30)

式中:ζ為偏差誤差。

(31)

偏差b動態使用典型的“布朗運動”模型建模,即導數是高斯白噪聲,以捕捉參數緩慢時變性質:

(32)

為了計算線性化的誤差動態,首先對增強的右不變誤差進行微分。在執行鏈式規則并進行一階近似后得

(33)

誤差動態只通過噪聲wΩ和偏差誤差ζ依賴于估計軌跡。當沒有噪聲wΩ和偏差誤差ζ時,誤差動態對估計軌跡沒有依賴。現在可以從中構建一個線性系統,得到

(34)

測量方程不依賴于IMU的偏差。因此,對增強的右不變誤差,H矩陣可以簡單地附加零以滿足維度要求。線性更新方程成為

(35)

最終,包括陀螺儀偏差b的“增廣InEKF”方程,可以完整寫出。估計狀態使用以下一組微分方程進行預測傳播。

(36)

增廣的右不變誤差動態的協方差通過解Riccati方程計算

(37)

式中:矩陣A,B由式(34)給出。估計狀態更新方程為

(38)

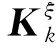
(39)

3.4 離散化

在前面的章節中,濾波狀態傳播方程是連續時間的。然而,為了實現濾波過程,這些方程需要離散化。為此,對慣性測量量(即輸入)做零階保持,并進行積分。偏差動態是簡單的高斯噪聲,因此,離散形式確定性動態方程為

(40)

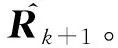
(41)

式中:Δt=tk+1-tk。為了更新協方差,需要解一個連續時間的Riccati方程(37),它的解析解為[13]

Pk+1=Φ(tk+1,tk)PkΦ(tk+1,tk)T+Qd

(42)

其中,離散噪聲協方差矩陣為

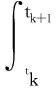
(43)

狀態轉移矩陣Φ(tk+1,tk)滿足:

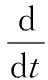
(44)

求解式(44)得到[12]:

(45)

與狀態轉移矩陣類似,離散噪聲協方差矩陣也有一個解析解。不過實踐中,這個矩陣通常被近似為Qd≈ΦQΦTΔt。

4 數值模擬

使用 MATLAB 對前述不變擴展卡爾曼濾波算法進行仿真實驗,證明了所提出的不變擴展卡爾曼濾波方案的有效性。為了進行較為真實的仿真,首先從一個實際的陀螺儀上采集一組真實的角速率測量值。采樣速率為60 Hz。從R0=I開始,真實姿態矩陣由下式迭代生成:

Rk+1=Rk(ΩΔt)

初始陀螺儀偏差的真值設置為b0=[-0.1 0.1 0.1]Trad/s。然后生成一組數據為

(46)

陀螺儀噪聲wΩ有0.001 rad/s的標準差,陀螺儀偏差b的過程噪聲方差為Σb=0.0012Irad2/s4,而磁力計和加速度計噪聲Σa=Σm=0.01I。

將所提方案與經典的MEKF相比較,MEKF同樣采用旋轉矩陣作為姿態表示。進行50次Monte Carlo實驗,得到兩種方案的姿態估計誤差的變化如圖1所示。

圖1 姿態估計誤差的變化圖

從圖1中可以看出,由于兩種方案都采用旋轉矩陣表示,在濾波預測階段過程方程也相同,從而姿態估計誤差相差極小。由于姿態誤差呈周期性波動,故采用最后15 s的誤差平均值進行比較。50次仿真結果的均值與標準差如表1所示。

表1 50次仿真最后15 s姿態估計誤差

可以看出在姿態估計誤差方面InEKF比MEKF略有優勢。而對陀螺儀偏差的估計如圖2所示。

圖2 陀螺儀偏差估計誤差的變化圖

由圖2可以看出在姿態估計誤差相對穩定之后,InEKF估計的陀螺儀偏差要更加接近真值。圖3是濾波過程結束時刻陀螺儀偏差誤差的箱線圖。

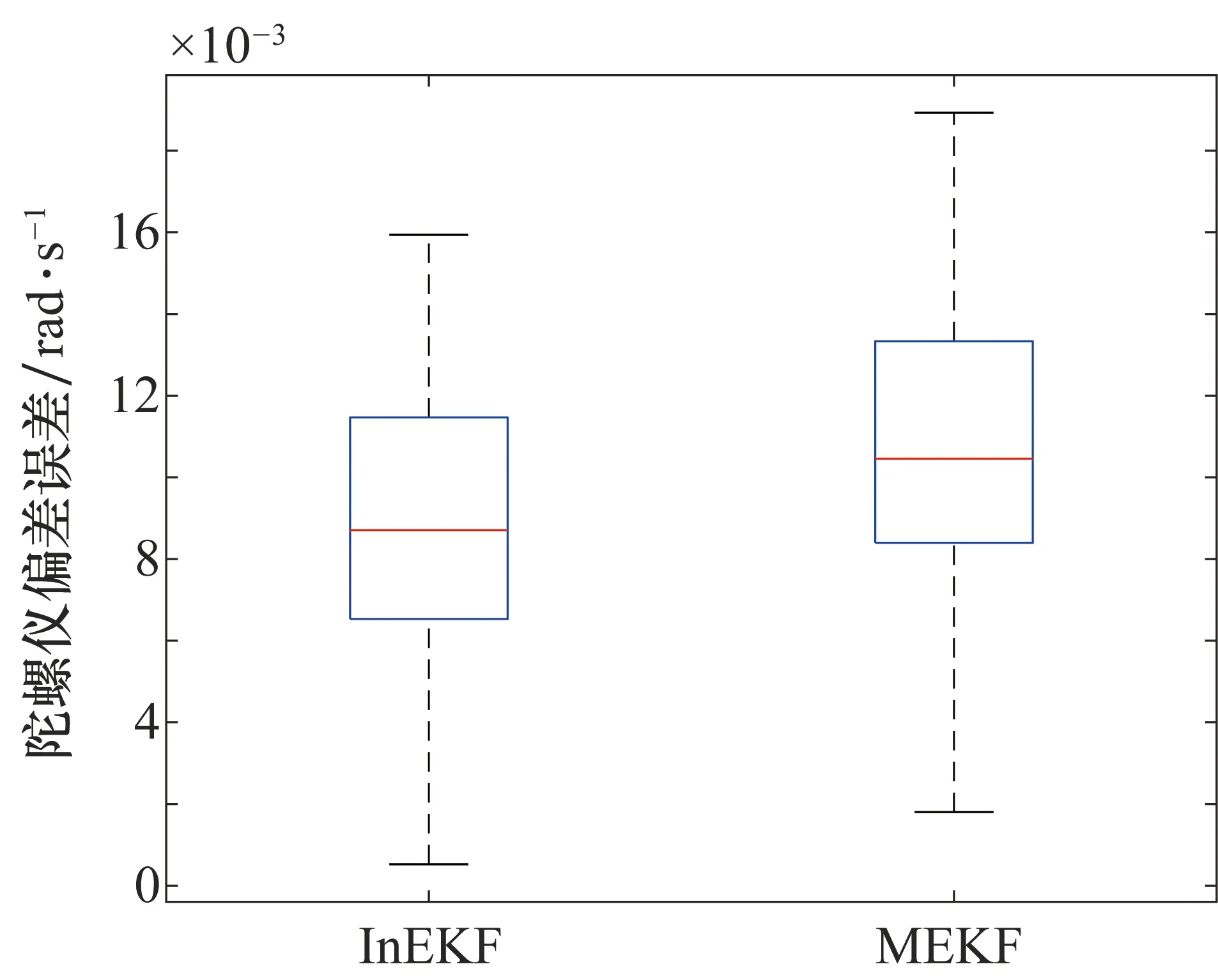
圖3 濾波過程結束時刻陀螺儀偏差誤差的箱線圖

由圖3可以看出InEKF估計的陀螺儀偏差整體更優,InEKF誤差的平均值為0.008 947,而MEKF的平均值為0.010 850,InEKF比MEKF的精度提高了約18%,具體數據如表2所示。某次濾波過程開始階段和中間一段時間陀螺儀偏差的變化如圖4和圖5所示。

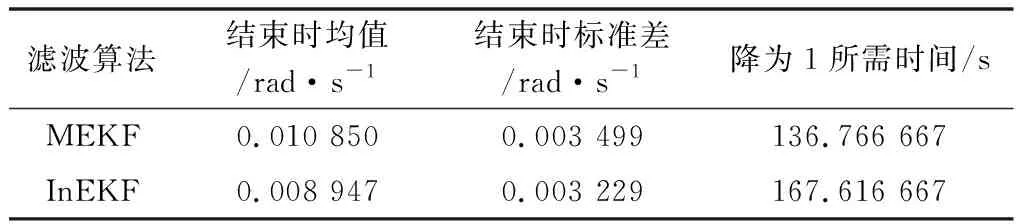
表2 仿真中陀螺儀偏差誤差統計量

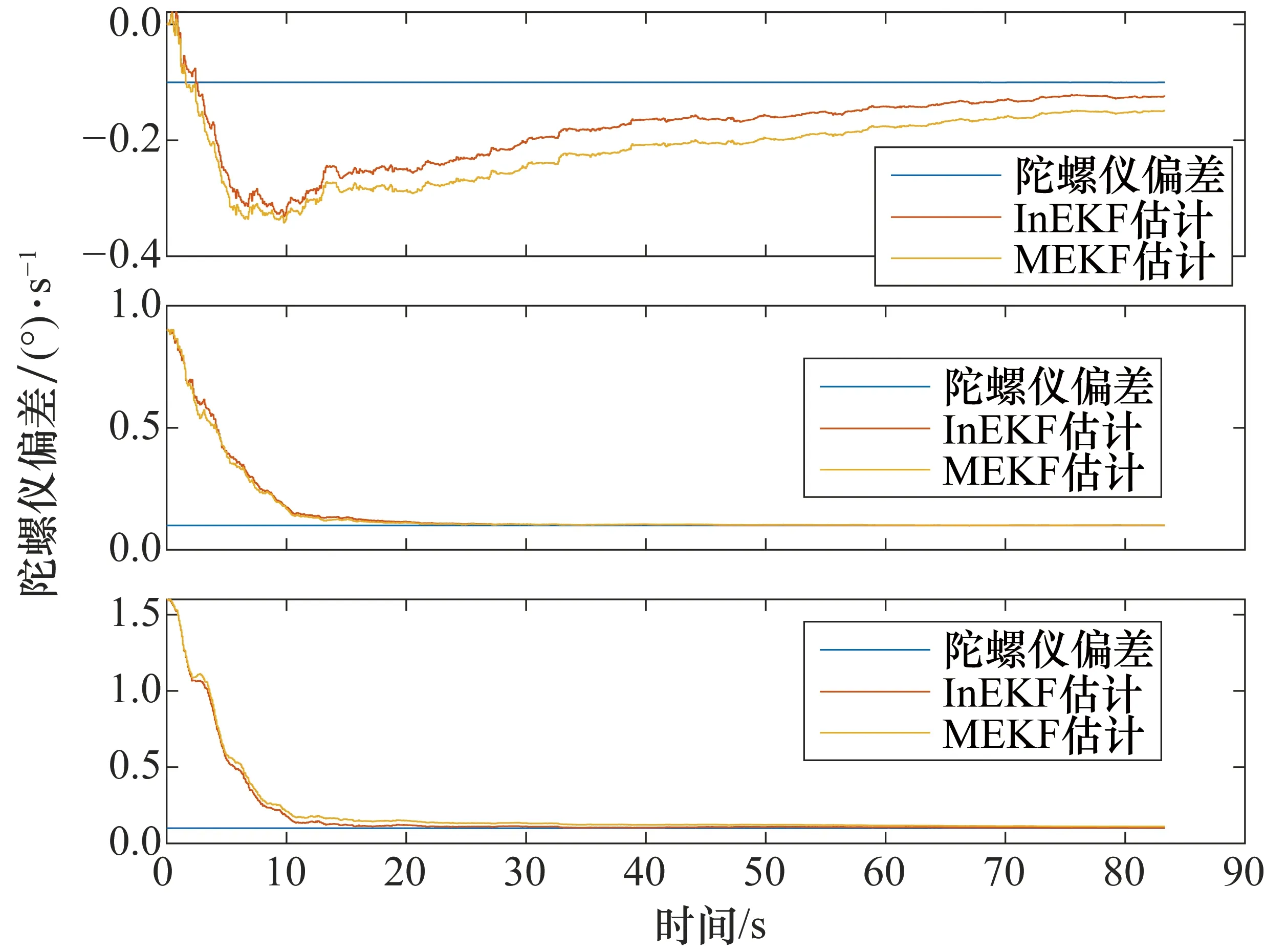
圖4 某次仿真開始階段陀螺儀偏差的變化圖

圖5 某次仿真中間階段陀螺儀偏差的變化圖

從變化軌跡可以看出,InEKF的估計比MEKF收斂到真值附近的時間更快,證明了該方法具有優越性。

5 結束語

本文提出了一種InEKF算法,用于同時估計無人機姿態和陀螺儀偏差。借助特殊正交群SO(3)的李群特性,推導出一種在SO(3)×R3中運動的連續時間隨機非線性濾波算法,該算法的主要特點是將姿態估計結果和估計誤差表示為SO(3)的元素,通過指數映射推導誤差動態的近似一階線性微分方程,從而減小誤差動態對當前估計值的依賴,增強了濾波算法對初值不確定的魯棒性。通過仿真將該算法與經典的MEKF算法進行比較,仿真結果表明所提出的濾波算法在保持姿態估計精度的同時,能提供更優的陀螺儀偏差估計,驗證了該算法在精度和濾波收斂性等方面具有優越性。