煤層中瓦斯滲流規律的技術研究

郭 玥,郭 輝

(1.山西煤礦安全培訓中心,太原 030000;2.山西能源學院 安全工程系,太原 030000)

近年來隨著淺部煤炭資源的耗盡,煤炭開采深度不斷增加,地質條件日趨復雜,瓦斯涌出量大幅度增加。我國的煤炭開采每年以10～25 m的速度向深部移動,深部煤炭開采面臨更加嚴重的瓦斯問題[1-2]。因此,研究煤體在不同壓力梯度下的應變及瓦斯滲流規律,對于礦井災害的治理是非常重要的。

滲流規律有兩種表現形式:一種是線性流動規律,即達西定律;一種是非線性流動規律,即Forchheimer方程。達西定律是達西在1856年發現的,該規律表明壓力梯度與流速之間存在線性關系;20世紀60年代,周世寧[3]通過對滲流力學的研究提出了線性瓦斯流動理論,這為瓦斯開采和煤礦安全管理提供了理論基礎;福希海默研究發現壓力梯度-流速曲線呈非線性偏離達西定律,可以用Forchheimer方程來描述;Teng等[4]通過試驗數據證實并嚴格驗證了一個通用的Forchheimer方程來表征非達西滲流現象;劉建等[5]研究了達西滲流與非達西滲流轉變的臨界點及Forchheimer方程的參數量化問題;王藝霖[6]建立了一種基于非達西Izbash冪律方程的井流控制方程,用于描述裂隙中的非達西流動;張天軍等[7]研究了不同產狀對煤體滲流特性的影響,分析了流體在裂隙煤體中的非達西滲流機理;Luo等[8]通過在真三軸應力下進行煤體滲流試驗,分析了不同主應力下煤體的非線性滲流特性;張天軍等[9]研究了位移與滲透壓改變時不同級配結構下破碎煤樣的滲流參量及雷諾數變化規律,破碎煤樣的流速與壓力梯度均呈現非線性關系。

有關破碎煤體的壓力梯度應變及瓦斯滲流規律已在理論和試驗上得到了廣泛研究,但在井下,煤體的裂隙面積多種多樣,不同的裂隙面積所對應的應變和滲流規律沒有得到明確的區分。本文在前人的研究基礎上,以預制裂隙煤體為研究對象,研究不同裂隙面積的煤體在三軸加載壓縮試驗中的力學特性以及三軸滲流試驗的滲流規律,這對煤炭深度開采中的瓦斯治理具有重要的意義。

1 瓦斯運移規律及特性

根據壓力梯度與流速之間的關系可將滲流分為線性流動與非線性流動。如果壓力梯度與流速呈線性關系,則稱滲流為達西滲流,可以用達西定律來描述;如果壓力梯度與流速呈非線性關系,則用Forchheimer方程來描述非達西滲流現象。

1.1 瓦斯線性流動理論

線性流動滲流理論認為,煤層中的瓦斯運移符合線性滲透定律,即達西定律[10-12]。

(1)

式中:v為流速,m/s;μ為瓦斯動力黏度系數,Pa·s;K為煤層滲透率,m2;dL為與流體流動方向一致的極小長度,m;dPr為在dL長度內的壓差,Pa。

經驗證明,當Re在1～10時,屬低雷諾數區,流體的運動符合達西定律。20世紀60年代,周世寧通過對滲流力學的研究提出了線性瓦斯流動理論,這為瓦斯開采和煤礦安全管理提供了理論基礎。

1.2 非線性瓦斯流動理論

在高滲流速度情況下,達西定律不再符合隨著壓力梯度增加,裂隙中的瓦斯流速增加,流體的慣性效應明顯,導致壓力梯度與流速之間不再為嚴格的線性關系。Forchheimer方程能夠更好地描述瓦斯在孔隙中的非線性滲流[13-14]:

(2)

式中:?p為壓力梯度,MPa/m;ρ為流體密度,kg/m3;β為非達西滲流因子,m-1。

由上式可知,當裂隙中瓦斯流速足夠小時,非線性項ρβv2遠小于線性項μ2v/K,非線性項忽略不計,則可表示為?p=μ2v/K,即此時的流體滲流符合達西定律。當裂隙中瓦斯流速足夠大時,非線性項不可忽略,流體滲流不符合達西定律,需要用Forchheimer方程來描述流體流動。

2 試驗設備及方案

2.1 試驗設備

試驗使用WYS-800微機控制電液伺服三軸瓦斯滲流試驗裝置進行測試。三軸滲流系統如圖1所示。裝置主要由計算機控制系統、氣路控制系統、液壓系統和主機等組成。其中,液壓站提供系統動力,計算機測控系統通過控制電液伺服閥和電液伺服缸對試樣加載,主機三軸室內放置試樣進行測試。試驗過程由計算機控制系統按規定的加載過程進行控制,可實時監測并記錄試驗數據。

2.2 預制裂隙試樣

將事先加工好的Ф50 mm×100 mm的標準煤樣采用SK5616金剛砂線切割機對試樣進行進一步切割加工,如圖2所示。其主要參數為:電源220 V,行程160 mm×200 mm×200 mm。其加工流程為:①安裝0.25 mm的金剛砂線;②將標準試樣安裝固定到工作臺上調整切割位置;③在計算機程序輸入需要切割加工的尺寸、切割速度;④設定好程序后發出加工指令,開始切割標準試樣。將制備的Ф50 mm×100 mm的標準煤樣沿長軸線切割,按照預期方案切割成5種不同裂隙面積的試樣,如表1所示。制得的煤樣如圖3所示。

(a) 三軸力學滲流儀結構圖

(b) 三軸力學滲流儀

圖2 SK5616金剛砂線切割機Fig.2 SK5616 diamond wire cutting machine

圖3 切割完成煤樣Fig.3 Cutting coal samples

表1 預制裂隙試樣表Table 1 Prefabricated fracture samples

2.3 試驗方案

本次試驗是為了驗證預制裂隙試樣載流體通過時其壓力梯度與流速的關系。通過調節減壓閥來控制壓力梯度,通過排水集氣法測試流量,得到不同裂隙面積試樣、不同圍壓下的壓力梯度-流速曲線。具體試驗方案如表2所示。

表2 試驗方案Table 2 Test plans

在三軸加載力學滲流過程中控制軸壓為12 kN,設置4級不同有效圍壓條件,在每級圍壓下設置5級注氣壓力。所有測點測試完畢后,以0.02 kN/s的速率施加軸向應力,直至試樣失穩破碎。本次試驗所用滲流氣體為氮氣。氮氣的密度在標準狀態下(1大氣壓,0℃)為1.250 6 g/L,在室溫下(20℃)的動力黏度為17.8×10-6Pa·s。氣體的密度和動力黏度都會受到溫度和壓力等條件的影響,在不同的條件下數值可能會有所變化。為了調節不同的壓力梯度,需要不斷調整注氣壓力。有效應力公式為[15-16]:

(3)

式中:σ0為有效應力,MPa;σ1為軸壓,MPa;σ2為圍壓,MPa;p1為進口壓力,MPa;p2為出口壓力,MPa。

當調節進口壓力時,有效應力會發生改變,影響裂隙通道,從而影響試件的滲流特性,此時無法控制裂隙面積為單一變量,所以需要設定圍壓跟蹤模式來保證有效應力不變,使得裂隙面積為單一變量。

圍壓跟蹤模式:即控制有效圍壓不變。有效圍壓是基于有效應力的原理計算而得,其計算公式如下:

σ′=σ-αp.

(4)

(5)

式中:σ′為有效圍壓,MPa;σ為圍壓,MPa;α為奧比系數,取1;p為平均壓力,MPa。

試驗步驟如下:

1)安裝試樣。在試件側面均勻涂抹一層704有機硅密封膠,放入熱縮管中安裝在三軸室底座上,用熱烘槍烘烤熱縮管表面,使熱縮管與試件充分貼合,防止氣體從試樣與熱縮管之間流出。在試樣上下兩端擰緊喉箍,與圍壓加載油路隔絕,避免液壓油浸入試樣,堵塞氣路。

2)安裝環向引伸計。將環向引伸計固定在試件中部,然后調節環向引伸計的精度,使其可以精確測得加載過程中試樣的徑向變形。

3)安裝好三軸室,向三軸室注入液壓油后,排出三軸室內的空氣,防止加載圍壓時因空氣擠壓造成圍壓值波動。之后將圍壓加至1 MPa,將圍壓和軸壓交替加載,直到圍壓與軸壓值滿足試驗需要。通入滲流氣體,等待氣體吸附解吸平衡后通過集水排氣法測試單位時間內氣體通過試件的體積,即流量。

4)調節減壓閥至設定的壓力值,待流量穩定后,測試流量值。之后繼續調節減壓閥以調節壓力梯度,直到此圍壓下的全部壓力梯度的流量測試完成后,將減壓閥關閉。

5)重復上述操作,按照試驗方案加載不同有效圍壓,測試試件流量。

6)以0.02 kN/s的速率繼續對試樣加載軸壓,直至試樣失穩破壞,監測加載過程中的軸向變形和徑向變形。

7)試樣破壞后,卸載圍壓和軸壓,保存數據。整理試驗設備準備進行下一次試驗。

3 試驗結果及分析

3.1 三軸力學試驗結果及分析

不同裂隙面積試樣在三軸加載過程中的偏應力-軸向應變曲線與偏應力-徑向應變曲線,如圖4所示。不同裂隙面積的試樣在三軸加載過程中,偏應力與軸向應變曲線的變化趨勢相似[17-20]。試件在進行三軸加載過程中,其變形經歷了4個階段,分別是壓縮密實階段、彈性階段、屈服階段和破壞階段。試樣在三軸壓縮過程中的壓密階段表現并不明顯,幾乎與彈性階段相同,在圍壓加載階段已經完成試樣的壓密。

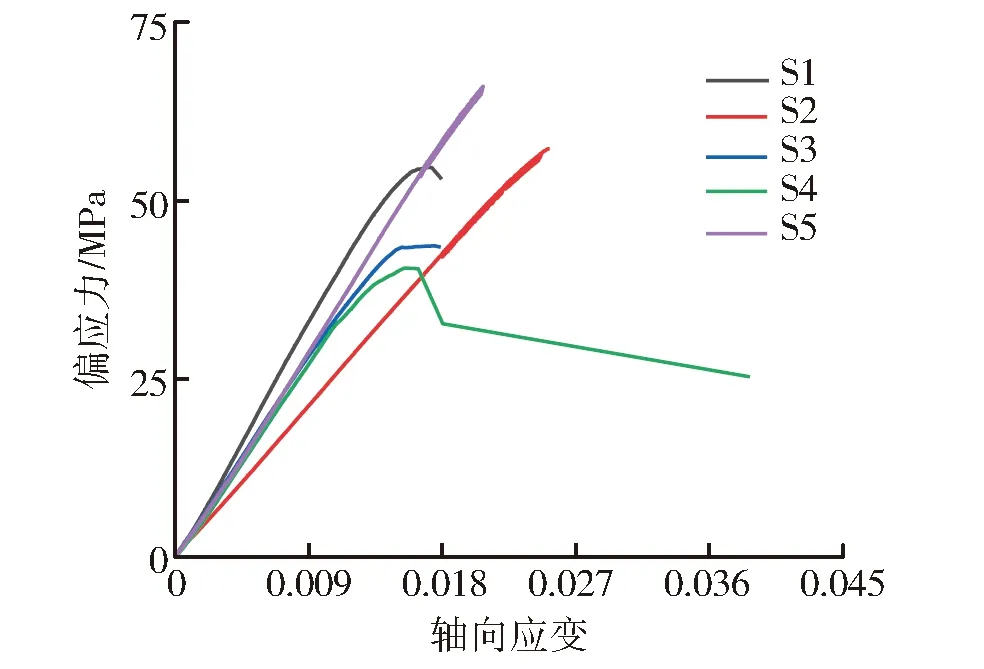
(a) 偏應力-軸向應變

(b) 偏應力-徑向應變

圖4(b)為試樣偏應力-徑向應變曲線。隨著軸向應力的不斷增加,煤樣中的孔隙逐漸減小,試樣中的顆粒開始發生位移,最終會出現破壞。偏應力-徑向應變曲線通常呈現先線性增長后逐漸趨于平緩的趨勢。當軸向應力增加到一定程度時,曲線的斜率開始下降,直至試樣完全破壞。

彈性模量可用于反映試件抵抗彈性變形的能力。完整試樣的彈性模量值最高,可達到3 706.19 MPa,其次是裂隙面積為50 cm2的試樣較完整試樣的彈性模量降低了9.73%,并且該試樣的三軸抗壓強度最大。當試件裂隙面積為12.5 cm2時,試件的彈性模量較完整試樣降低了35.81%,隨后裂隙面積逐漸增加,試件的彈性模量也隨之增大,但始終小于完整試樣的彈性模量。

試件垂直方向上的應變與載荷方向上的應變之比的負值,稱為試件的泊松比[21]。試件的泊松比可以作為材料剛性特性的一個重要參考指標。三軸壓縮試樣力學參數如表3所示。裂隙面積為25 cm2的試樣泊松比最大值為0.44,與完整試樣相比,裂隙面積為25 cm2的試樣泊松比增加了37.5%,完整試樣的泊松比最小值為0.32,表明完整試樣在三軸壓縮過程中,縱向的應變變化相對較大,而橫向的應變變化相對較小,該試樣的剛度較大,具有更好的抗壓性和穩定性。

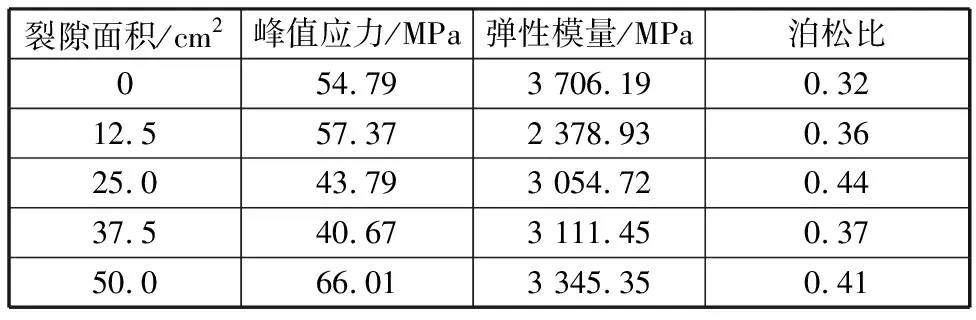
表3 三軸壓縮試樣力學參數Table 3 Mechanical parameters of triaxial compression specimens

3.2 三軸滲流試驗結果及分析

3.2.1壓力梯度-流速分析

圖5為完整試樣在不同有效圍壓下的壓力梯度與流速的擬合曲線。通常認為,煤體中瓦斯的滲流遵循達西定律,即呈線性流動狀態,所以對完整試樣的壓力梯度與流速進行了線性擬合。由圖5可知,隨著壓力梯度的增大,流體的流速逐漸增加。試樣在三軸壓縮加載的過程中,有效圍壓逐漸加載,試樣受到的有效應力逐漸增大,試樣內部的孔-裂隙逐漸閉合,流體通過的難度增大,試樣滲透率減小,使得擬合曲線的斜率逐漸增大。

由圖6可知,裂隙面積為12.5 cm2、25.0 cm2、37.5 cm2和50.0 cm2的試樣在不同有效圍壓下的壓力梯度擬合曲線變化趨勢不再為嚴格的線性關系,而是出現了不符合達西定律的明顯現象,這是因為貫穿裂隙試樣發生了滲透失穩[22]。隨著有效圍壓的增大,試樣的裂隙逐漸閉合,流體在裂隙中的流動難度增大,滲透率K逐漸減小,非達西滲流因子β增大,則在相同速度下,非線性項的值越大,造成的壓力梯度損失越大,由非線性項造成的非達西效應越顯著。

圖5 S1試樣在不同有效圍壓下的壓力梯度-流速擬合曲線Fig.5 S1 sample fitting curves of pressure gradient and flow rate under different effective confining pressures

(a) S2

(b) S3

(c) S4

(d) S5

Forchheimer方程有明確的物理意義,其中的線性項表示由黏滯力造成的壓力梯度損失,非線性項表示由慣性力造成的壓力梯度損失。通過試驗數據擬合得出線性項系數和非線性項系數,從而得出試樣的滲透率K及非達西滲流因子β。由壓力梯度與流速擬合出的Forchheimer方程的線性項系數,及非線性項系數如表4所示。

表4 滲透率與非達西滲流因子擬合參數表Table 4 Fitting parameters of permeability and non-Darcy seepage factors

圖7為在相同有效圍壓下,不同裂隙面積試樣的壓力梯度與流速的擬合曲線。由圖可知,在有效圍壓一定時,隨著裂隙面積的增加,裂隙的過流能力越大,滲流速度逐漸增加。而裂隙面積較小的試樣過流能力較小,其非達西滲流因子β較大,導致在相同流速下,其非線性項較大,則由慣性力造成的壓力損失較大。所以裂隙面積越小的試樣其壓力-梯度流速曲線越向縱軸(壓力梯度軸)凹。

當試樣所受到的有效圍壓一定時,裂隙面積為12.5 cm2的試樣在同等壓力梯度下流速最小。在同一圍壓下,裂隙面積較小的試樣與裂隙面積較大的試樣相比,裂隙面積較小試樣達到相同的滲流流速需要更大的壓力梯度。裂隙面積為25 cm2的試樣壓力梯度-流速曲線與裂隙面積為12.5 cm2的試樣曲線較為接近。當裂隙面積增加到37.5 cm2時,其壓力梯度-流速曲線與25 cm2試樣的曲線相距較遠。當試樣裂隙面積為50 cm2時,其壓力梯度-流速曲線與前3個試樣的壓力梯度-流速曲線相比出現偏離,壓力梯度-流速曲線凹向橫軸(流速軸)。有效圍壓為7 MPa、8 MPa、9 MPa、10 MPa的不同裂隙面積壓力梯度與流速曲線的變化趨勢大致相同。

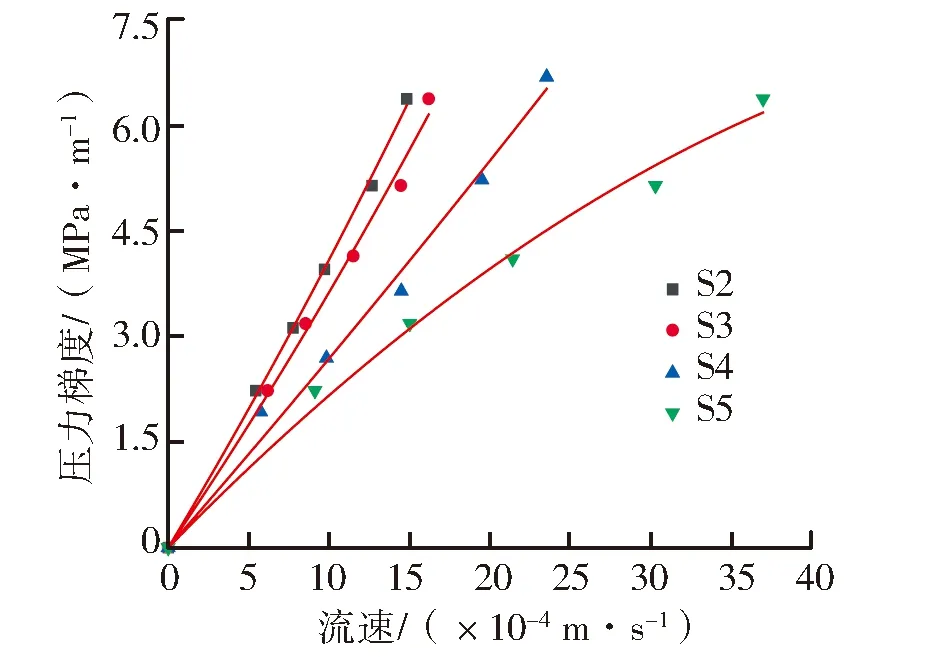
(a) 7 MPa

(c) 9 MPa

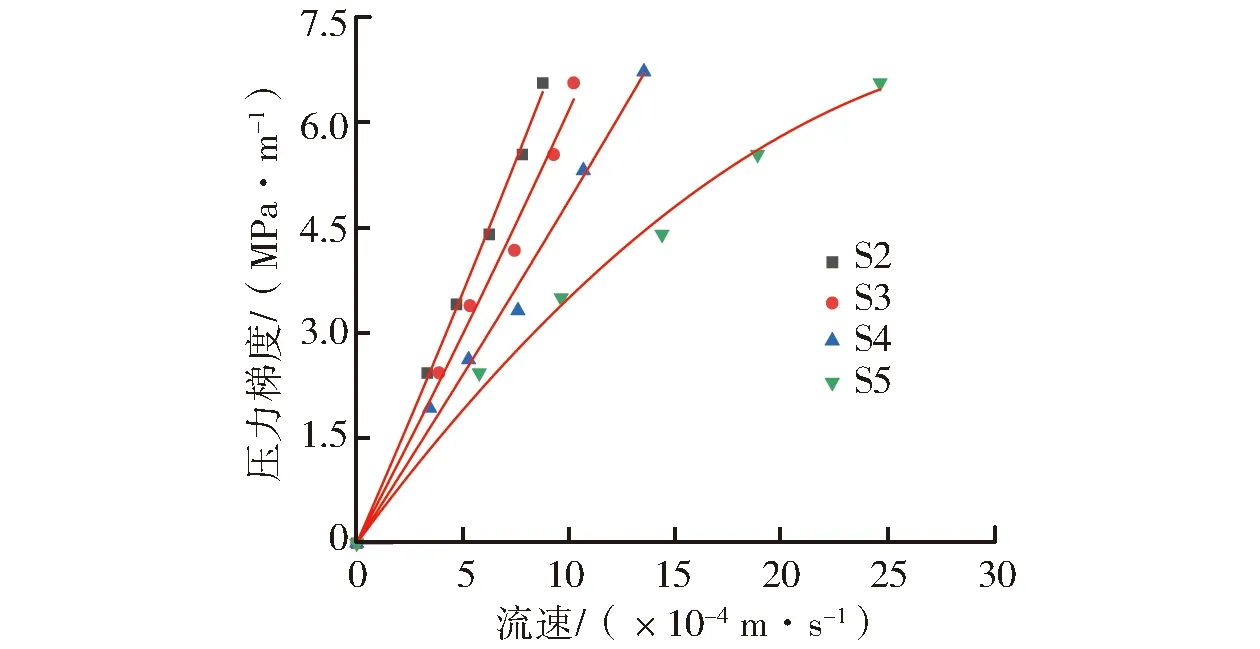
(d) 10 MPa

3.2.2Forchheimer方程線性項與非線性項系數分析

圖8為擬合得出的滲透率隨有效圍壓的變化關系。在不同裂隙面積試樣的滲流過程中,隨著有效圍壓的增大,煤體滲透率依次降低。當有效圍壓為10 MPa時,不同裂隙面積試樣的滲透率都為最小值。在相同有效圍壓下,裂隙面積越大的試樣,其滲透率越高。

圖8 滲透率隨有效圍壓的變化趨勢Fig.8 Variation of permeability with effective confining pressure

如圖9所示,非達西滲流因子受有效圍壓的影響,試樣受到的有效圍壓越大,裂隙面積為12.5 cm2、25.0 cm2、37.5 cm2的非達西滲流因子β依次上升。裂隙面積為50 cm2的試樣隨著有效圍壓的增大,非達西滲流因子的絕對值逐漸增大,有效圍壓與非達西滲流因子呈正相關。

圖9 有效圍壓-非達西滲流因子β隨有效圍壓的變化關系Fig.9 Relationship curves of effective confining pressure and non-Darcy seepage factor β

圖10為不同圍壓下裂隙面積與滲透率關系變化曲線。在有效圍壓一定時,隨著試樣裂隙面積的增加,試樣的滲透率逐漸增加。當有效圍壓為8 MPa時,隨著試樣裂隙面積的增加,試樣滲透率增加的趨勢不明顯。裂隙面積由12.5 cm2增加到25.0 cm2時,試樣的滲透率增加了7.3%,增加幅度較小。不同有效圍壓的裂隙面積與滲透率曲線變化趨勢大致相同。在相同有效圍壓下,裂隙面積越大的試樣,其滲透率越大。

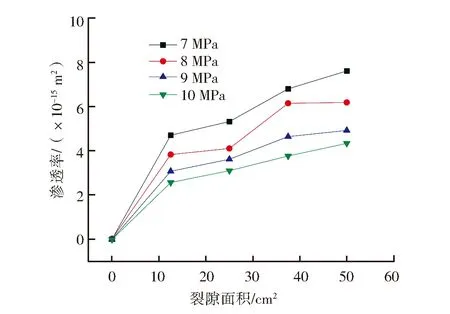
圖10 裂隙面積-滲透率關系曲線Fig.10 Relationship curves of fracture area and permeability

圖11為不同圍壓下裂隙面積與非達西滲流因子β的關系變化曲線。隨著裂隙面積的增加,非達西滲流因子β逐漸減小。裂隙面積為50 cm2時,非達西滲流因子出現負值。在有效圍壓為7 MPa時,其非達西滲流因子β的絕對值大于裂隙面積為12.5 cm2的β值。隨著有效圍壓的增加,非達西滲流因子β的絕對值逐漸增大。

圖11 裂隙面積-非達西滲流因子β關系曲線Fig.11 Relationship curves of fracture area and non-Darcy seepage factor β

3.2.3非線性程度影響系數分析

福希海默數F0表示Forchheimer方程中非線性項與線性項的比值,即流體克服慣性力壓力損失與克服慣性力壓力損失之比。引入Forchheimer數作為判斷流體狀態從達西滲流轉換為非達西滲流的標準。

(6)

式中:F0為福希海默數。

將式(6)代入非線性程度影響系數求解式中,得出非線性影響程度系數α與福希海默數F0存在如下關系:

(7)

當非線性程度α大于0.1時,福希海默數F0大于0.11,因此當F0>0.11時,由流體克服慣性力引起的壓力梯度損失不可忽略。F0=0.11為劃分線性滲流與非線性滲流的臨界值。

圖12為不同有效圍壓下福希海默數F0與壓力梯度的關系曲線。隨著壓力梯度的增加,裂隙試樣的福希海默數F0逐漸增大。在壓力梯度較高時,福希海默數F0大于0.11,流體在裂隙中的滲流狀態發生轉換,由符合達西定律的線性滲流變為Forchheimer型非線性滲流。

圖12 福希海默數F0-壓力梯度關系曲線Fig.12 Relationship curves of Forchheimer numberF0 and pressure gradient

4 結論

本文采用三軸力學滲流儀對不同裂隙面的試樣進行了三軸力學及滲流試驗。得出如下結果。

1)不同裂隙面積的試樣在三軸加載過程中的偏應力-軸向應變曲線的變化趨勢基本一致。在三軸壓縮加載過程中,試樣在三軸壓縮過程中的壓密階段表現并不明顯,幾乎與彈性階段不可區分,在圍壓加載階段已經完成試樣的壓密。

2)開展不同圍壓下的滲流試驗,研究不同壓力梯度下預制裂隙試樣的非線性滲流特性。用Forchheimer方程擬合試驗測得壓力梯度與流速,裂隙試樣滲流流態呈現出顯著的非線性流動特征,在相同的壓力梯度增量下,流體流速的增加低于線性遞增的值。

3)隨著有效圍壓的增大,試樣的裂隙逐漸閉合,流體在裂隙中的流動難度增大,滲透率K逐漸減小,非達西滲流因子β增大;隨著裂隙面積的增加,滲透率K逐漸減小,非達西滲流因子β逐漸減小。