雙饋風電場抑制電網低頻振蕩的自適應附加控制策略
劉新宇, 王 森, 曾 龍, 原紹恒, 郝正航, 逯芯妍
(1. 華北水利水電大學 電力學院,鄭州 450011; 2. 廣東工業大學 自動化學院,廣州 510006;3. 貴州大學 電氣工程學院,貴陽 550025)
現代工業的迅猛發展已經造成對煤和石油等化石能源的過度依賴和嚴重的環境污染等一系列問題.由于風力發電(簡稱風電)不會污染環境且風能屬于可再生能源,風能的充分利用對能源結構的調整和實現“雙碳”目標具有重要意義.近些年,伴隨著大規模風電并網的快速發展,建設更大規模的風電場以及遠距離輸電問題應運而生[1].由于風能具有隨機、不穩定的特點,而我國的用電負荷中心往往距離風電場比較遠,輸電線路負荷較重,加之風電場又處于相對薄弱的電網末端,所以給風電并網系統的穩定性造成較大影響[2].
大規模的風電并網、長距離的輸送線路、風能不穩定這些問題大大降低了系統的阻尼,因此當系統發生跳閘、三相接地短路或是小擾動干擾時,易引起傳輸線路的功率低頻振蕩.迄今為止,已經發現多次電力系統低頻振蕩現象,給電力系統帶來很大影響.在國內,隨著中國新疆維吾爾自治區北部地區風電裝機容量的迅速增加,自2014年6月以來,廣域測量系統已反復捕獲次同步頻率下的持續功率振蕩[3].在國外,德克薩斯電力可靠性委員會電網中已經發現多次4 Hz的低頻振蕩[4].在此類嚴重事故中,低頻振蕩甚至會激起附近渦輪發電機的強烈扭轉振動,從而導致發電廠的所有發電機跳閘.因此,有必要增強包含風電的混合電力系統的阻尼,以提高系統頻率穩定性.
為保證風電并網系統穩定安全運行,很多國家已經出臺相關的政策規定在風電機組中必須帶有可以增強系統阻尼的附加環節.文獻[5]中提出基于區域極點配置的風電系統弱阻尼低頻振蕩抑制控制策略,采用線性矩陣不等式的區域極點配置方法設計反饋控制器,將系統中的弱阻尼振蕩模式配置到所控制區域,提高系統的阻尼比.文獻[6]中以系統的頻率偏差值作為輸入,根據不同的風速設置槳距角,設計基于變系數的下垂控制調節風力發電機的有功出力,為系統注入正阻尼.文獻[7]中根據兩區域電力系統模型,選擇合適的輸入輸出變量,對輸入函數和狀態函數求導得到反饋控制律,提出基于非線性控制算法的附加阻尼控制策略,可以有效地處理阻尼控制器中的非線性環節.文獻[8]中將雙饋風力發電機(DFIG)和電力系統靜態穩定器(PSS)放在一起,建立系統的狀態方程,定義系統振蕩模式對傳遞函數的靈敏度,然后運用定義的靈敏度優化控制參數,該控制策略能有效抑制系統低頻振蕩.文獻[9]中分析含DFIG的風電系統可能會引起低頻振蕩的原因,對比基于復轉矩系數法的4種控制策略,為開發最優控制策略以抑制DFIG系統在不同條件下的軸系振動提供了參考.文獻[10]中提出一種有源-無源協調雙通道功率調制阻尼控制器,該控制器可以較好地發揮DFIG轉子側控制器的阻尼控制能力.文獻[11]中提出基于電力系統穩定器和功率振蕩阻尼器的魯棒協調控制策略改善低頻振蕩阻尼,該方法使用改進的基于特征值的目標函數實現,并用灰狼優化器進行優化.文獻[12]中提出基于阻耗系數的附加阻尼模糊控制策略,通過控制轉子側換流器調節DFIG無功功率來增強系統阻尼,進而抑制系統低頻振蕩.文獻[13]中提出一種基于主動抗擾控制的有功無功附加阻尼控制器,能起到很好的抑制負阻尼的作用.文獻[14]中提出一種基于自抗擾控制器的廣域阻尼控制器協調優化策略,采用人工蜂群算法對自抗擾控制器和廣域阻尼控制器進行協調優化,提高系統阻尼水平.文獻[15]中設計基于頻率反饋的大規模柔性負荷控制策略和統一潮流控制器串聯側功率反饋附加控制策略,最后運用遺傳算法優化協同控制參數,得到最優控制策略.文獻[16]中分析有功功率環節和無功功率環節附加阻尼控制的差異,提出一種基于bang-bang調制的混合快速阻尼控制策略和基于二階滑模的雙饋風電機組魯棒阻尼控制策略,對電力系統區間振蕩有很好的抑制效果.文獻[17]中利用狀態反饋的方法將系統輸入、輸出作線性化處理,將非線性系統線性化,最后提出基于超螺旋算法的阻尼控制器,該控制方法不依賴于系統的詳細建模參數,具有良好的工程應用價值.
綜上所述,國內外學者針對電力系統區域間功率低頻振蕩已經進行了深入的研究,也提出大量的附加阻尼控制器設計方法.然而,大多數設計方案將系統中聯絡線功率或發電機功角偏差等參數作為輸入,忽略系統平衡點變化后的動態特性對低頻振蕩的影響,在系統平衡點附近線性化的基礎上設計類似于PSS結構的附加阻尼控制器,而很少有研究將DFIG自身轉子電壓和磁鏈的關系應用到阻尼控制器設計上.本文對DFIG的動態頻率響應和轉子勵磁電壓與磁鏈之間的關系進行研究,結合終端滑模變結構控制的思想,設計基于轉子磁鏈偏差的快速終端滑模附加阻尼控制器,并證明該系統的收斂性和穩定性.該控制器將磁鏈的偏差作為輸入,輸出一個附加信號到轉子側功率控制環節,進而控制轉子側換流器,調節DFIG出力,抑制系統低頻振蕩現象.最后,通過仿真驗證本文所提控制方法對系統低頻功率振蕩的影響.
1 DFIG響應阻尼調節能力分析
DFIG系統在三相靜止坐標系中的模型階是一個多變量、高階次、強耦合、非線性的復雜時變系統.為了便于計算和控制,運用坐標變換將其轉換到兩相同步旋轉d-q坐標系下進行分析[18].忽略定子繞組壓降和電磁暫態變化過程,將定子電壓定向于d軸上,DFIG定子輸出有功功率(Ps)、無功功率(Qs)和轉子磁鏈方程可表示為
(1)
式中:Ls、Lr、Lm分別代表定子自感、轉子自感和定轉子互感;ω1為同步轉速;ψqs為d-q坐標系下定子q軸磁鏈分量;ψdr、ψqr分別為d-q坐標系下轉子磁鏈分量.
(2)
式中:Rr為轉子電阻;ωs=ω1-ωr為發電機轉差角速度,其中ωr為發電機轉子轉速;udr、uqr分別為轉子d-q軸電壓分量;Ug為電網側電壓.
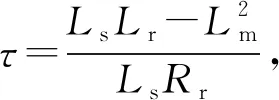
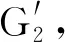
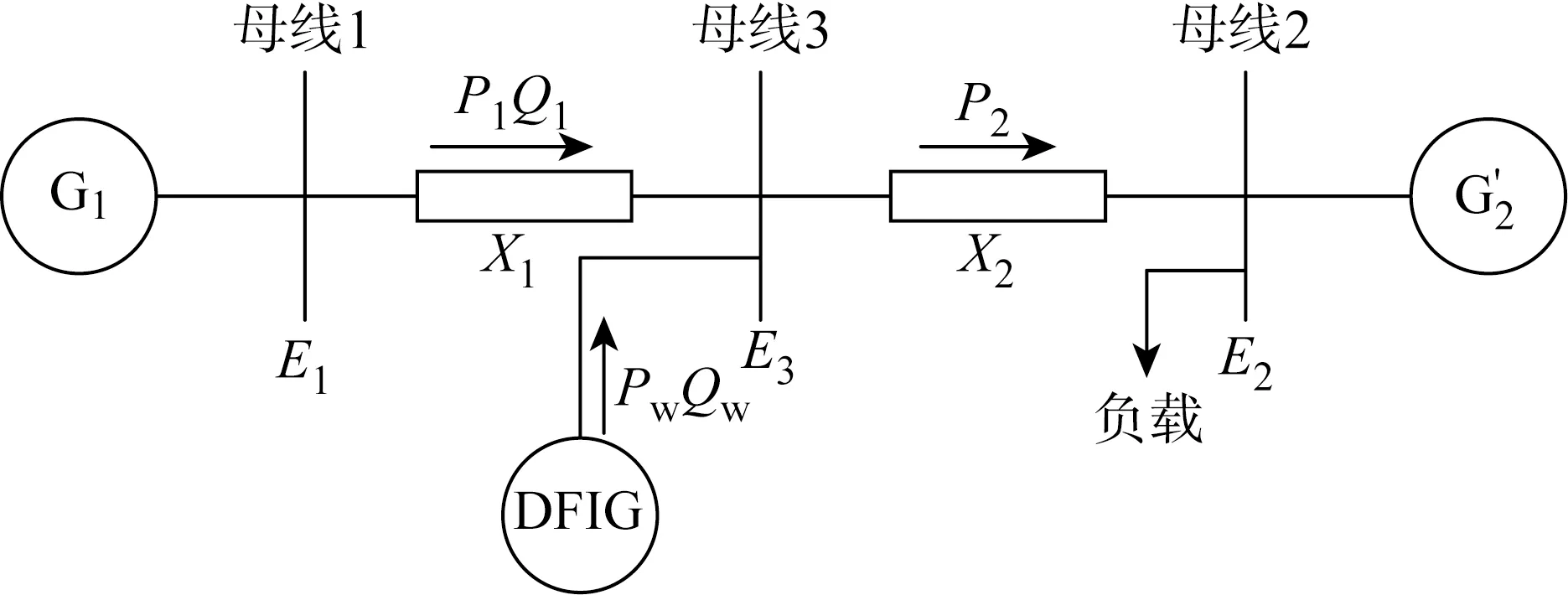
圖1 兩區域電力系統模型Fig.1 Two-region power system model
2 終端滑模附加控制器設計
由上述分析可知,調節DFIG輸出有功功率可以提高系統的阻尼水平,因此可以通過調節DFIG的有功功率改善系統阻尼水平,進而抑制系統區域間的低頻振蕩.
2.1 系統滑模面與控制律設計
由式(2)可得,DFIG運行過程中,轉子外加電壓和轉子磁鏈之間的關系如圖2所示.圖中:s為DFIG轉差率.DFIG在發電狀態時,將轉子磁鏈分量ψdr、ψqr作為系統的受控輸出,則轉子勵磁電壓udr、uqr為系統的控制輸入.為達到系統快速控制的目的,將終端滑模變結構控制方法運用到DFIG轉子磁鏈控制方案之中,設計轉子磁鏈控制器,使系統磁鏈跟蹤期望磁鏈,確保系統在指定時間內迅速達到穩定狀態.
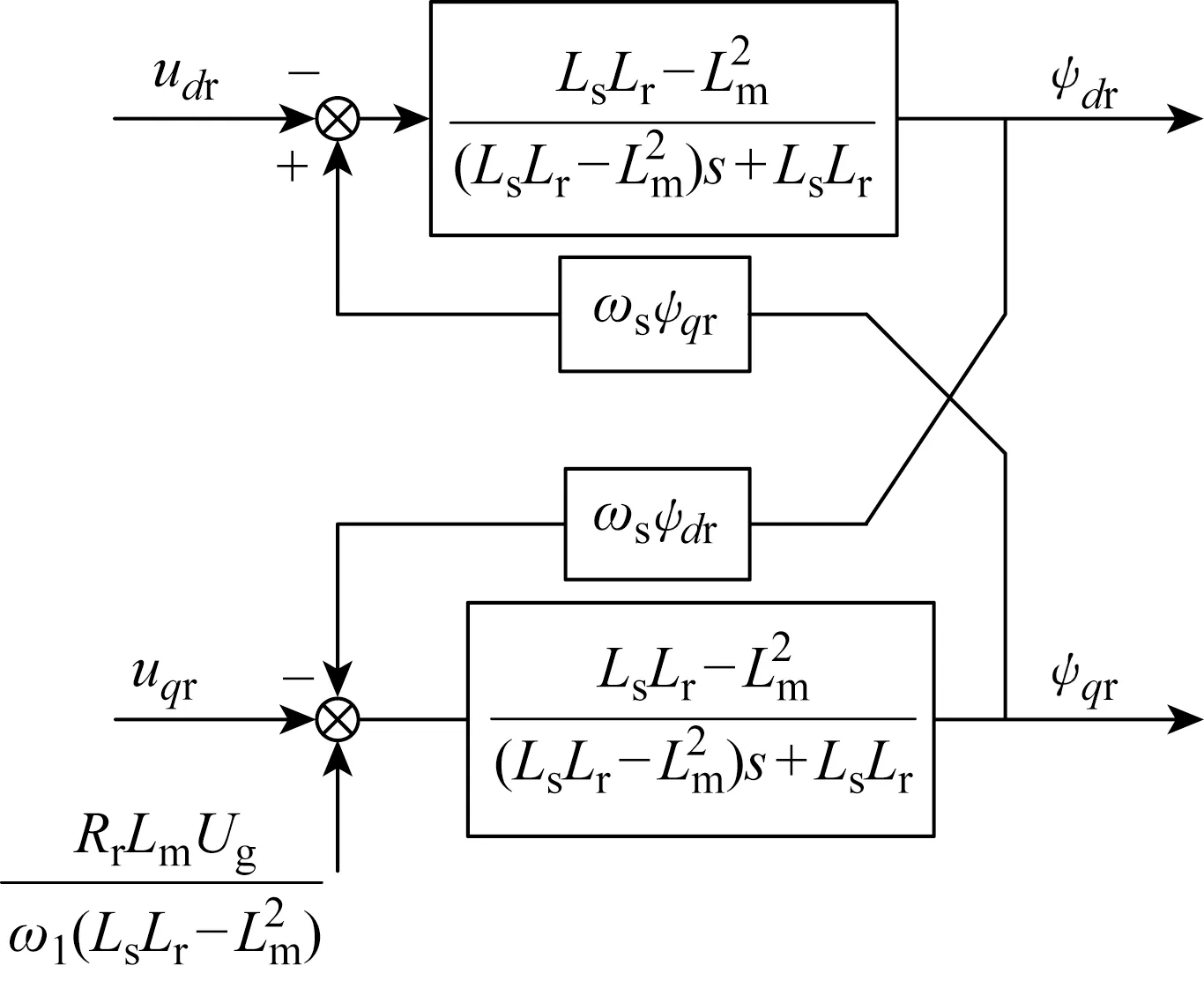
圖2 DFIG轉子外加電壓與磁鏈之間的關系圖Fig.2 Relationship between applied voltage and flux linkage of DFIG rotor
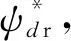
(3)
基于以上分析,設計如下滑模面:
(4)
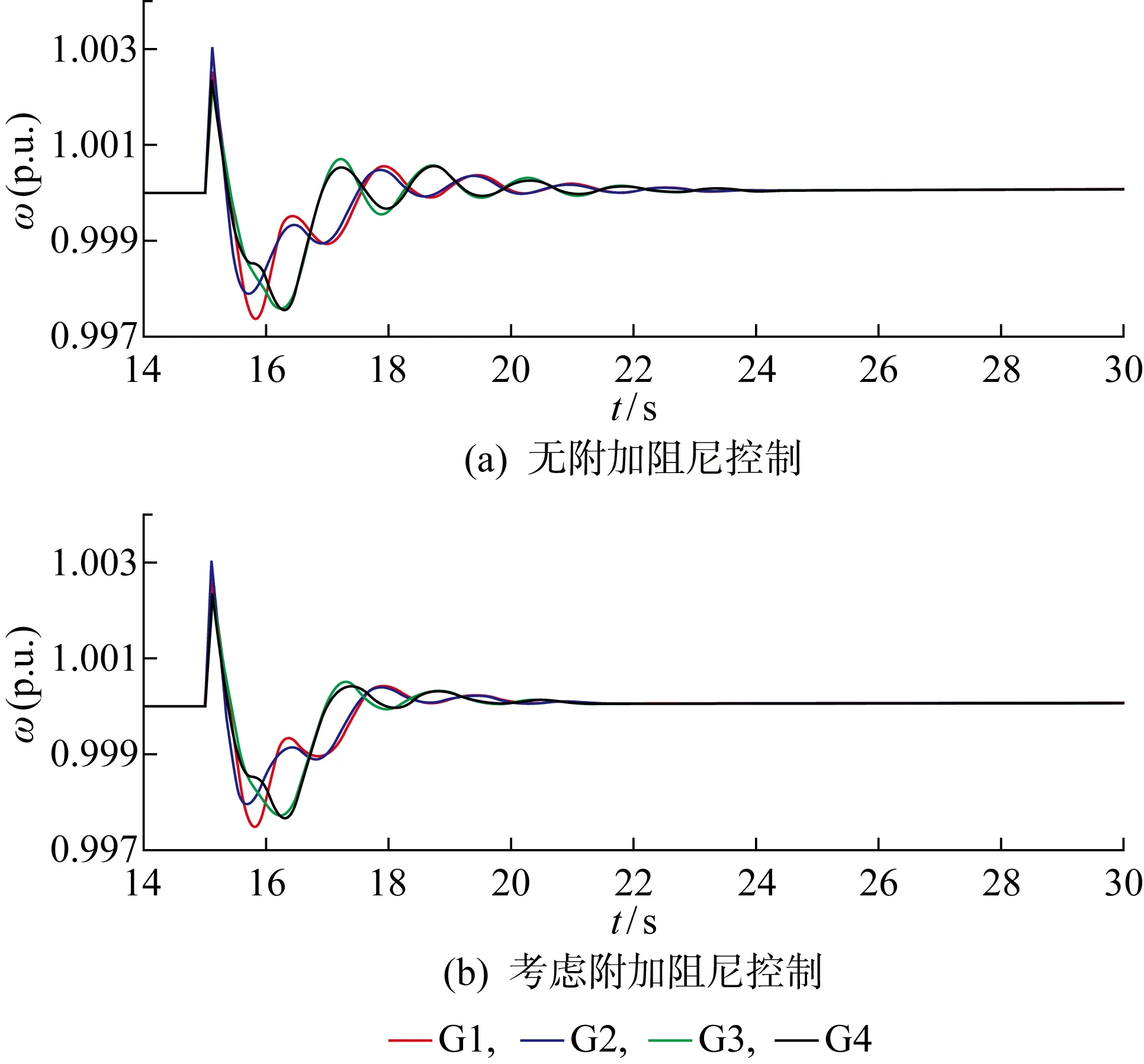
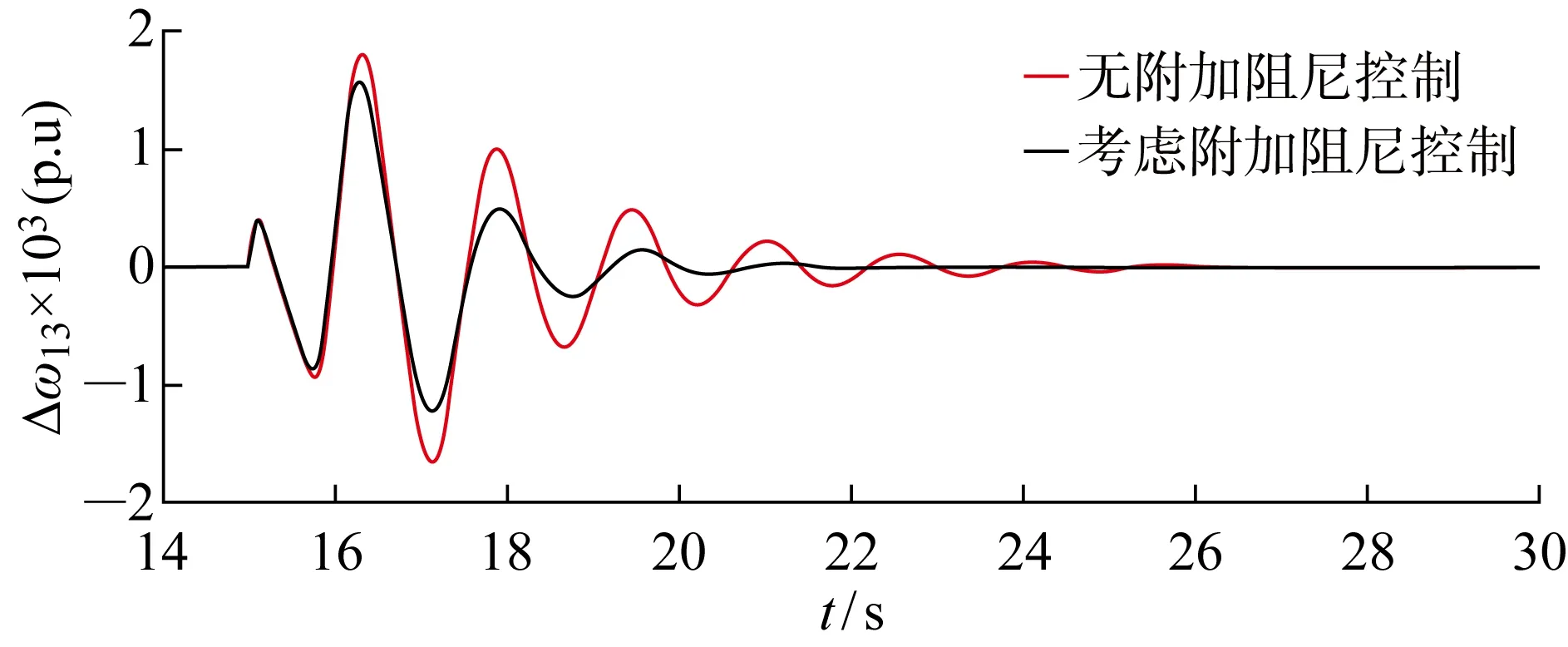
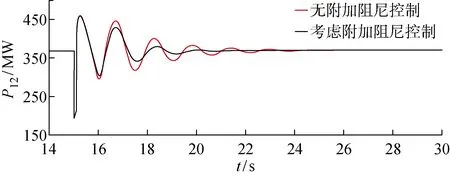
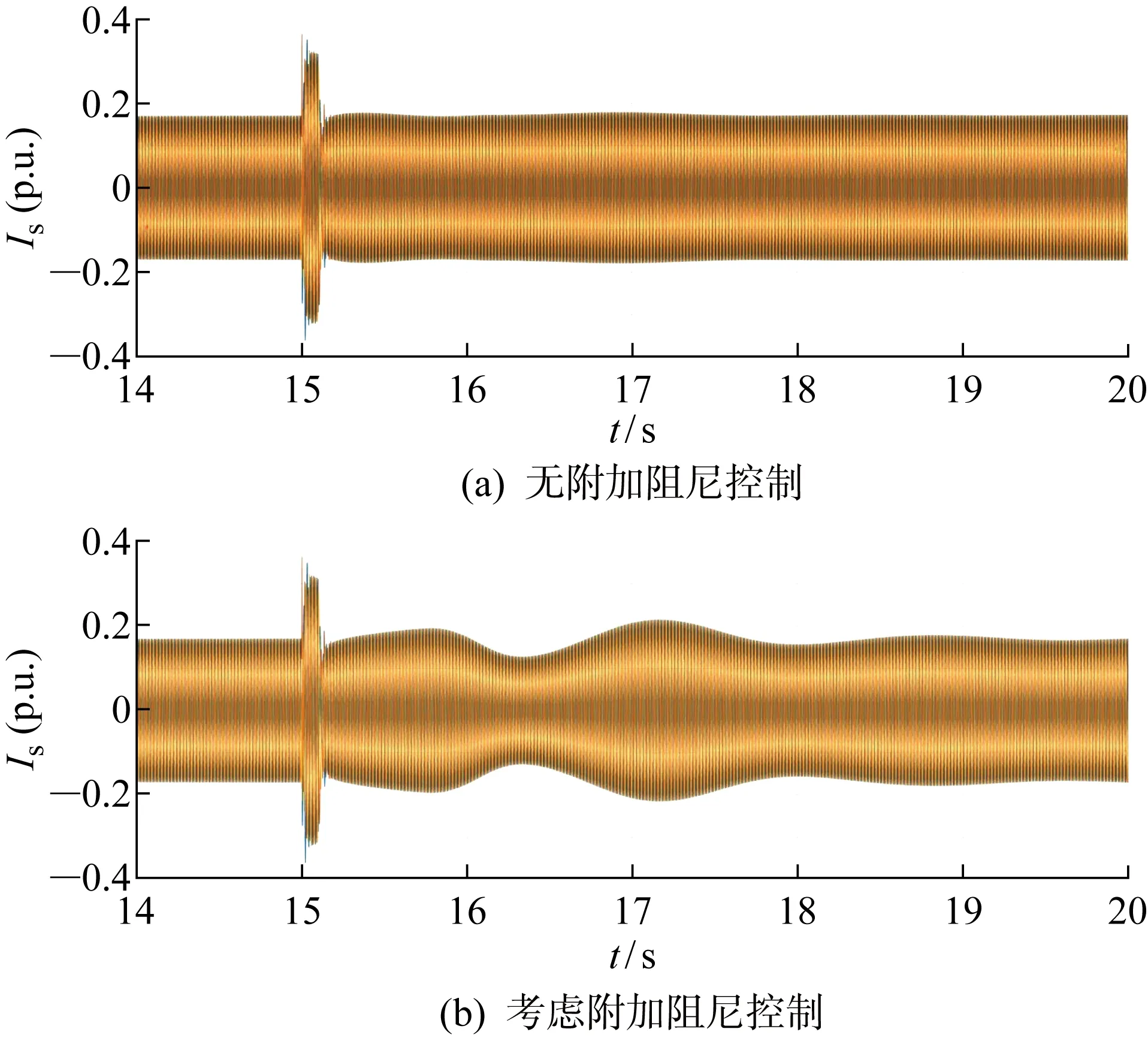
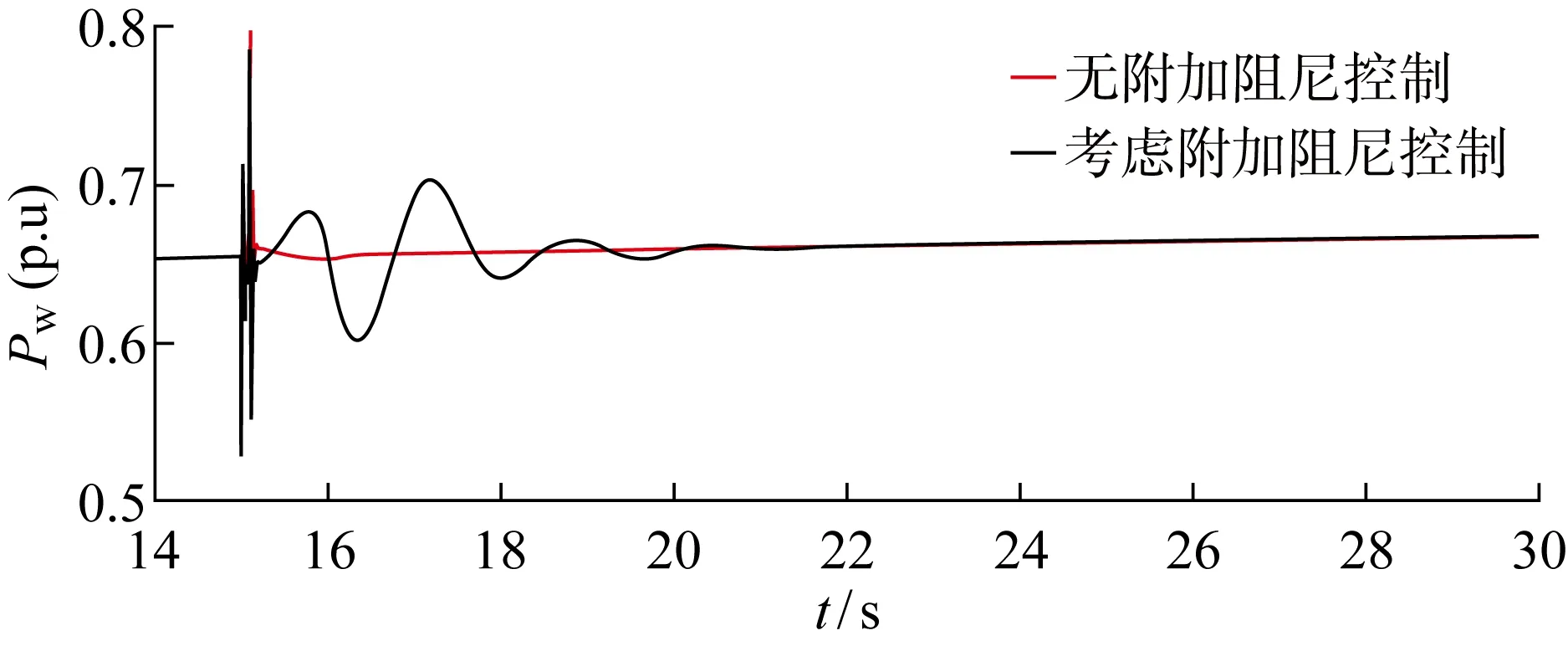
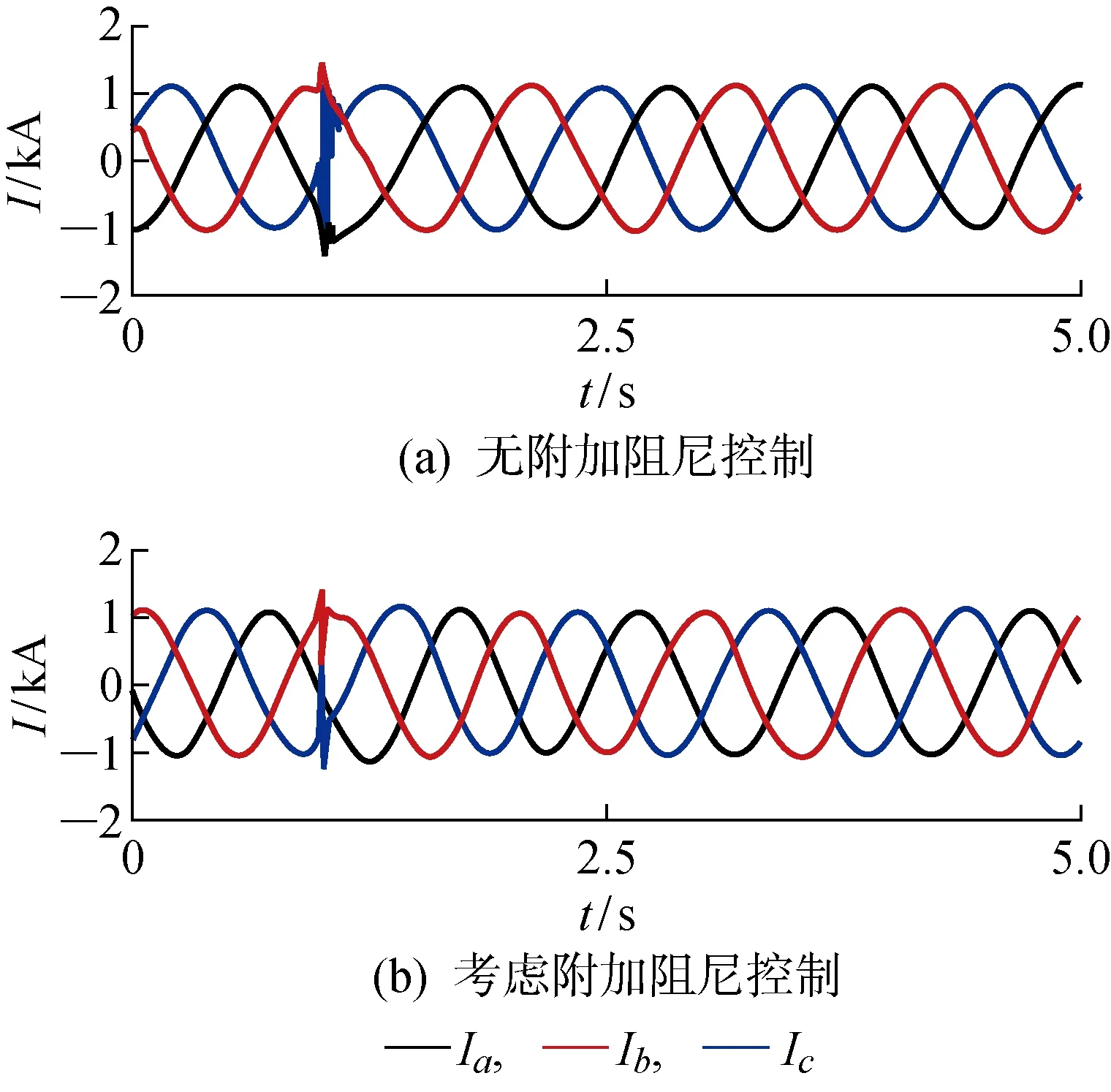
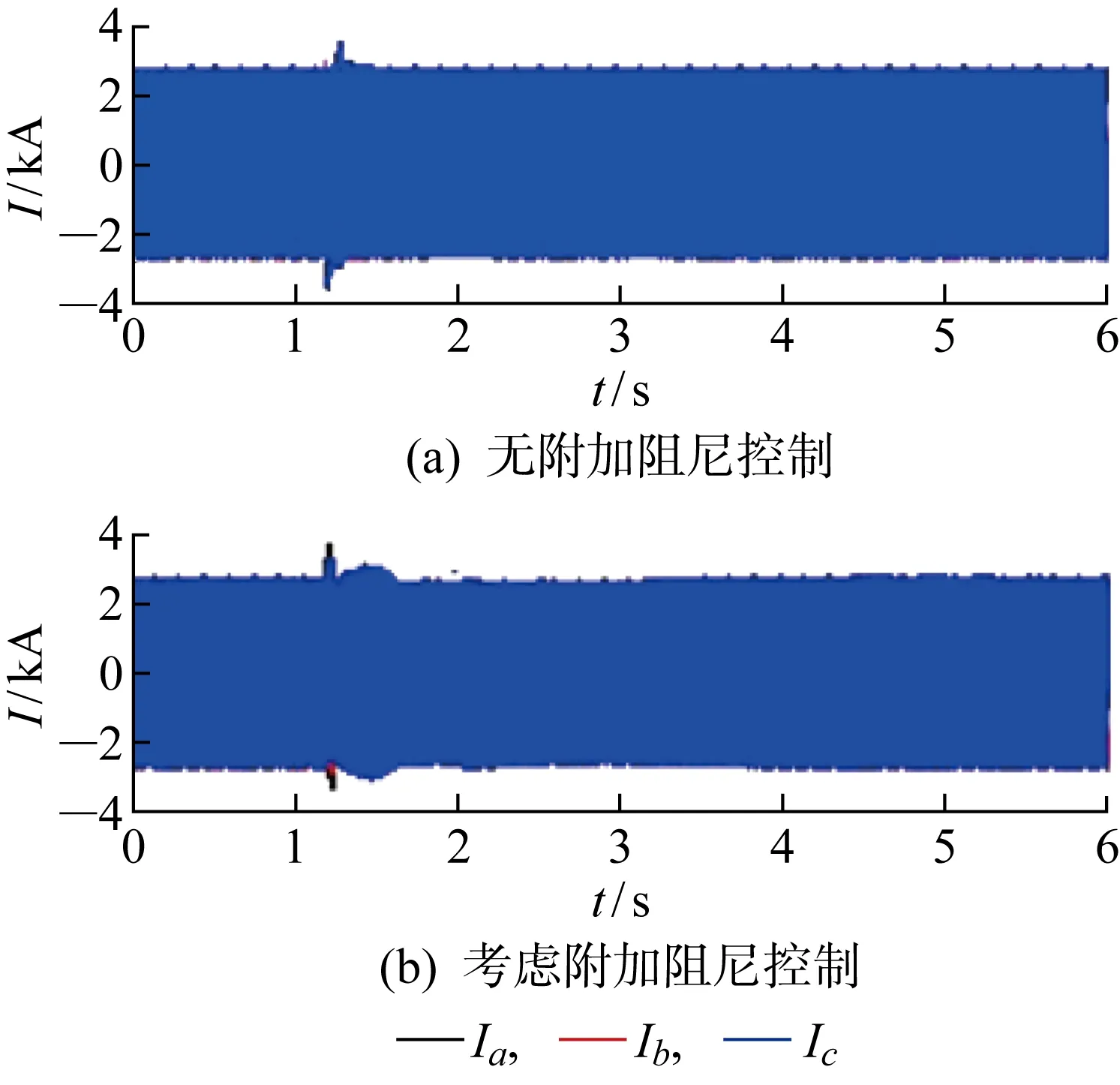
式中:參數ρ1>0;p1、q1為正奇數,且0 式(4)對時間求導得: (5) 將式(3)代入式(5)得: (6) 則轉子d軸磁鏈采用的控制律可設計為 udr=udreq+udrn (7) 式中:udrep、udrn分別為等效控制律和切換控制律,且滿足 (8) (1) 系統收斂性證明. 證明當Sd=0時,系統位于滑模面上,此時有 (9) 求解可得: (10) 則DFIG的d軸磁鏈狀態可在有限時間Δtd內快速收斂到0,證畢. (2) 系統穩定性證明. 證明取李雅普諾夫函數: V(t)=Sd(t)/2 (11) 求導可得: (12) 將式(6)代入式(12)可得: (13) 所以V(t)≤0,系統在李雅普諾夫穩定性理論上全局漸進穩定,證畢. 同理可得轉子q軸磁鏈控制律為 uqr=uqreq+uqrn (14) (15) 式中:參數ρ2>0;p2、q2為正奇數,且0 圖3 機側控制器模型Fig.3 Control model of machine side 系統中使能環節表達式如下: (16) 根據前文推導的快速終端滑模附加控制的原理設計附加阻尼控制器,在MATLAB/Simulink中建立如圖4所示的四機兩區域模型并進行仿真分析.圖中:G2、G3和G4為同步發電機,L1、L2分別代表區域1和區域2負荷. 仿真環境設置:設t=15 s時,兩區域聯絡線發生0.1 s的三相短路,此時系統由于阻尼不足,在聯絡線上發生功率振蕩;t=15.1 s時故障消除,系統恢復正常運行狀態.觀察無附加阻尼控制下和本文提出的附加阻尼控制策略下系統中各項參數的響應曲線. 圖5為同步發電機轉速振蕩曲線.圖中:ω為轉速.對比有、無附加控制的響應曲線可知,在考慮附加阻尼控制情況下的同步發電機轉子轉速響應曲線的振幅更小,更快趨于穩定,具有更好的阻尼特性.由圖6所示的同步機G1和G3轉子角速度的差值(Δω13)振蕩曲線可知,在考慮附加阻尼的情況下,G1和G3轉子角速度偏差振蕩的振幅和時間均減小.說明所提出的附加控制策略對系統同步發電機的振蕩有一定抑制作用. 圖5 同步發電機轉速變化曲線Fig.5 Speed curves of synchronous generator 圖6 同步發電機G1和G3轉子角速度偏差振蕩曲線Fig.6 Angular velocity deviation oscillation mode of synchronous generator G1 and G3 圖7為DFIG轉子勵磁電流(Ir)的變化曲線.對比圖7(a)和7(b)可以看出,當系統發生低頻振蕩時,在有附加阻尼控制情況下,故障期間DFIG轉子電流增大并有一段時間的振蕩響應,使DFIG及時發出有功功率支撐電網;在沒有附加阻尼控制情況下,故障期間DFIG轉子電流變化較小,不能很好地響應系統振蕩.圖8為兩區域聯絡線功率(P12)變化曲線,從圖中可以看出在考慮了附加控制的情況下,聯絡線功率振蕩的振幅明顯減小,并且更快地趨于穩定. 圖7 雙饋發電機轉子電流變化曲線Fig.7 Rotor current curves of DFIG 圖8 聯絡線功率振蕩曲線Fig.8 Power oscillation curves of transmission line 圖9為DFIG定子電流(Is)變化曲線.由圖可知,在無附加控制下,故障期間DFIG定子電流幾乎沒有變化.而在采用附加控制時,故障期間定子會短時振蕩現象,但其電流值仍在安全范圍之內,說明所提的附加阻尼控制策略在及時調節有功功率輸出的同時,并不會對雙饋風電系統帶來負面影響.圖10為DFIG有功功率(Pw)響應曲線.從圖中可以看出,在沒有考慮附加控制情況下,系統發生低頻振蕩之后,DFIG有功功率并沒有響應系統振蕩,而在考慮本文所設計的附加阻尼控制情況下,DFIG有功功率輸出能快速做出動態響應以提高系統的阻尼水平來抑制低頻振蕩. 圖9 雙饋發電機定子電流響應變化Fig.9 Stator current curve of DFIG 圖10 DFIG有功輸出振蕩曲線Fig.10 Response curves of DFIG active power 為了充分驗證所提附加控制策略在工程應用上的可行性,開發基于RTDS的風電并網四機兩區域實時仿真系統,主要仿真參數和離線仿真參數相同. 在RTDS平臺實驗中,系統運行至t=1.2 s時,在兩區域聯絡線上設置三相瞬時短路故障,傳輸線路出現功率低頻振蕩現象;t=1.4 s時,去除故障;監測DFIG定子電流、轉子電流和有功輸出響應情況以及系統振蕩頻率在是否考慮附加阻尼兩種情況下變化曲線,結果如圖11~14所示. 圖11 系統頻率變化曲線Fig.11 Frequency change curves of system 圖11為系統頻率(f)響應曲線.從圖中可以看出,在系統發生低頻振蕩故障期間,無附加阻尼控制情況下的系統頻率衰減較慢,振蕩持續時間相對較長.而采用所提附加控制之后,系統頻率振蕩曲線衰減較快,且振蕩的幅值更低,系統整體表現出更好的阻尼特性.圖12為DFIG有功出力響應曲線.由圖可見,當聯絡線發生功率振蕩時,如果考慮附加控制,DFIG就可以及時輸出更多有功功率響應其振蕩,為系統提供更多阻尼. 圖12 DFIG有功出力變化曲線Fig.12 Active output oscillation curves of DFIG 圖13為轉子勵磁電流實時仿真曲線.圖中:I為電流;Ia、Ib、Ic分別為abc三相電流.對比實驗結果可知:在采用附加阻尼控制策略的情況下,在故障期間,轉子勵磁電流增大,以便使雙饋發電機及時發出更多有功功率;而無附加阻尼控制下,轉子勵磁電流在故障期間幾乎沒有變化.而且從圖14可以看出,定子電流實時仿真結果與離線仿真時的動態響應曲線一致,均能夠保證DFIG的安全運行. 圖13 DFIG轉子電流變化曲線Fig.13 Rotor current curves of DFIG 圖14 DFIG定子電流變化曲線Fig.14 Stator current variation curves of DFIG 研究風電功率調節對系統低頻振蕩抑制問題,在DFIG的機側電流控制環上引入以增加電力系統阻尼為目標、基于李雅普諾夫穩定性理論的快速終端滑模附加阻尼控制器.利用MATLAB仿真測試與實驗驗證,在電力系統出現低頻振蕩故障時,所提出的快速終端滑模控制不僅可以快速調節DFIG有功功率,提高系統的阻尼水平,有效抑制低頻振蕩;而且在系統響應過程中,風力發電機的有功功率響應速度快、變化平滑,定子電流振蕩持續時間很短且振蕩幅值在安全范圍內,不會影響風電場安全運行,具有一定的應用參考價值.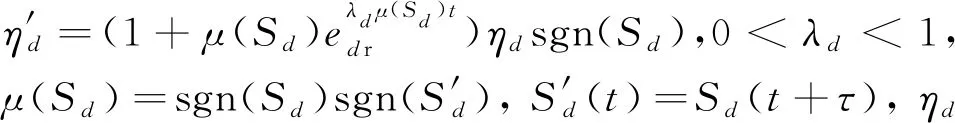

2.2 系統收斂性與穩定性分析
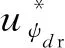

3 系統離線仿真與分析
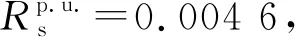

4 系統實時仿真實驗驗證與分析


5 結語

