軸承磨損的切片式半解耦損傷數值模擬方法*

李文婧,王泓暉,劉貴杰,田曉潔,李亞楠

(中國海洋大學 工程學院,山東 青島 266000)

0 引 言

隨著科學技術的快速發展,現代動車組裝備逐漸趨于多元化、復雜化。高速動車組服役環境變化多樣,常處于高速重載、劇烈沖擊振動等惡劣工況下,其一旦出現故障,勢必影響行車平穩性和安全性[1],嚴重時將造成不可估量的經濟損失及人員傷亡。

軸箱軸承作為高速動車組走行部的關鍵部件之一,其往往處于高速甚至超高速的運行狀態,此時軸承的磨損是一個非常突出的問題,有必要對軸箱軸承開展磨損損傷狀態分析與研究[2]。但目前,獲取磨損狀態信息不充分、難度大、成本高等因素是轉向架軸承磨損退化分析時存在的主要不足[3]。

因此,建立轉向架軸承的磨損模型,模擬在軌道激勵載荷因素作用下滾動軸承的磨損狀態,同時開展軸承的磨損損傷分析具有重要的研究價值和實際意義。

現階段,圍繞著模擬軸承的磨損退化研究,國內外學者已經展開了許多研究工作。HWANG S Y等人[4]利用網格刪除方式來復現軸承實際的磨損形貌,根據軸承幾何形狀和跳動值的變化,預測了軸承的磨損程度。SCHMIDT A A等人[5]通過實施節點位移偏移,得到了軸承接觸表面復雜的動態磨損行為,最后檢查了所有網格的畸變尺寸,得到的磨損量符合實際驗證結果。張金萍等人[6]使用ADAMS建立了軸承轉動系統虛擬樣機,通過改變內部間隙來獲得不同磨損狀態間的差異,最終得到了能夠有效反映軸承磨損狀態的特征變量。ASHRAF M A等人[7]利用有限元分析方法,探究了聚合物表面接觸的滑動磨損過程,從而確定了磨損體積隨時間的變化,并預測了磨損的幾何結構。MUKRAS S等人[8]運用非線性有限元分析方法,模擬了軸承磨損形貌變化,同時提出了數值積分方案,以及并行計算兩種不同的最小化磨損計算成本方法。

由于磨損的模擬方法通常需要多次迭代循環,計算耗時長、成本高,尤其對于軸箱軸承這類尺寸大且工況復雜的零部件,上述問題則尤為突出。為此,非常有必要探索一種在保證精度可靠的前提下能夠有效降低仿真時間成本的數值模擬方法。

依據以上論述,筆者以轉向架軸箱軸承為研究對象,結合Archard磨損模型[9],提出一種切片式半解耦磨損損傷計算方法,對三維軸承模型進行多組二維切片磨損狀態的仿真,利用高斯過程擬合切片的仿真結果,探究軸箱軸承內圈磨損分布規律。

在保證結果有效性的條件下,筆者最小化有限元磨損分析方法的計算時間,以期為轉向架軸承的磨損損傷分析方法提供依據和參考。

1 軸箱軸承磨損有限元分析方法

1.1 研究對象

為了研究軸箱軸承的磨損損傷分析方法,筆者選取CRH380A高速動車組轉向架軸承作為具體的研究對象。由于高鐵軸箱軸承基本使用雙列圓錐滾子軸承,其中兩列軸承的材料屬性以及幾何參數完全一致,所以筆者僅對其中的一列軸承進行分析。

單列圓錐滾子軸承如圖1所示。

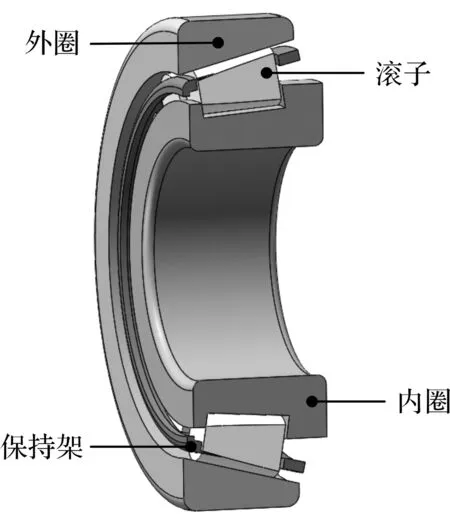
圖1 單列圓錐滾子軸承

對于高速動車組而言,其運行條件往往較為嚴苛。其內部軸箱軸承主要受到來自列車車體的垂向載荷、速度變化帶來的沖擊力和輪軌激勵等,軸承內部部件間的接觸狀態十分復雜[10-12]。

由于軸承內滾道外徑小,單位面積的接觸應力大,使得軸承內圈成為磨損的重災區。因此,筆者的研究側重于軸箱軸承內圈的磨損損傷分析,探究的重點也聚焦于其內滾道。

軸承各部件相關的材料參數如表1所示。

表1 軸承各部件材料參數

1.2 Archard磨損模型

由于軸箱軸承內部承受較大的接觸載荷,滾子的自轉運動導致滾動體與滾道間極易發生磨損失效。而磨損會改變滾道的幾何外形,從而改變滾子與滾道間的接觸應力,加速軸承的磨損失效進程。

Archard磨損模型目前被廣泛應用于材料磨損的計算場合,依據磨損體積的改變映射出材料磨損程度。

在該模型中,材料的磨損量與法向接觸力及滑動距離成正比,與材料的硬度成反比,即滾動軸承內圈的磨損量可表示為:

(1)

式中:Vm為磨損量,mm3;W為接觸面法向力,N;Lm為相對滑移距離,mm;H為材料硬度,N/mm2;K為磨損系數。

對于滾子軸承而言,內滾道與滾動體的接觸、外滾道與滾動體的接觸以及滾子與保持架的接觸為線或面接觸,接觸區域屬于小面積接觸。

其公式可改寫為:

(2)

式中:hs為磨損深度,mm;k為接觸面無量綱磨損系數與接觸面材料表面硬度的比值,即有量綱磨損系數,k=K/H;p為接觸面正壓力,MPa;s為接觸滑移距離,mm。

筆者利用有限元方法分析軸承磨損過程,將整個磨損過程離散成多個增量步的磨損增量堆積。

由于軸承內部的接觸情況是瞬時發生的,即滾子與內外滾道的接觸位置、接觸壓力以及滑移率都隨時間的變化而發生快速變化,并且也會隨磨損而變化;所以,此時筆者假設在每個非常小的增量步內,滾子與軸承內圈接觸點處的壓力和磨損系數是一個固定值。

其接觸點的磨損深度表示為:

(3)

式中:hn為在第n個增量步下的磨損深度;hn-1為第n-1個增量步下的磨損總深度;pn為第n個增量步下的接觸應力。

1.3 切片式半解耦損傷分析方法

磨損分析每個周期均需要考慮非線性接觸問題,若每個增量步都進行迭代計算,需通過大量迭代循環來模擬磨損演化過程;再加之接觸點發生磨損后,每個增量步對應的網格需要重繪,相應的計算成本大幅增加,并且模型計算效率也十分低下。

為應對此問題,筆者提出一種切片式半解耦損傷分析法。該損傷分析方法的關鍵步驟如圖2所示。

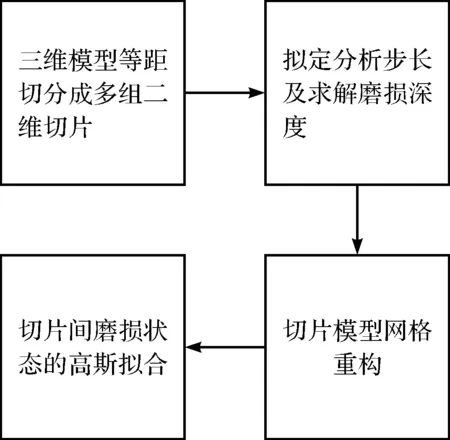
圖2 切片式半解耦損傷分析法關鍵步驟

在圖2中,切片式半解耦損傷分析方法的具體實施過程如下:

1)選取合適間隔,將軸承三維有限元模型沿徑向等距切分為多組,根據每組切面幾何特征,構建二維有限元模型,并將其作為后續分析的基本單位(后文稱之為二維切片模型);

2)將若干次磨損循環看作一個磨損周期Δq,該周期內的磨損體積變化很小,即可以認為在每個磨損周期內的應力場不因磨損而改變,即為定值,該過程稱為“半解耦”;同時設定該圈數Δq=10為磨損分析步長,并通過計算得到該步長下每個二維切片模型的磨損增量(深度),即:

(4)

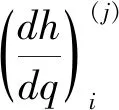
3)根據該磨損增量完成二維切片模型的幾何重構;

4)根據所有單元磨損增量更新軸承磨損狀態,重新求解新應力場,并進行下一段循環,直至達到預設的磨損仿真增量步或者磨損深度閾值;

5)期間,考慮到切片的原因,使三維軸承離散化,僅通過有限數量的二維切片模型難以直接給出軸承的磨損狀態,需借助高斯過程非線性問題的強大擬合能力,對切片模型之間的磨損狀態進行擬合。

假設多組二維切片計算得到的磨損深度數據集N={(xi,yi)|i=1,2,…,n},使用高斯函數表示:

(5)

式中:i為第i個接觸對;xi為在第i個接觸對下接觸點距軸承端面的距離;yi為對應接觸節點的磨損深度;ymax,xmax為待估計參數,S分別為函數曲線的最大值、最大值位置以及高斯曲線半寬度信息。

對上式等號兩側同時取對數,可以得到:

(6)

將右側平方公式展開可得:

(7)

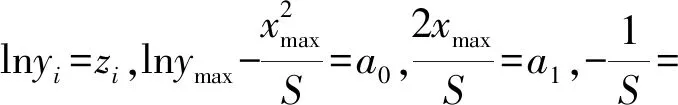
(8)

將其簡化為:

Z=XA

(9)

再依據最小二乘法,矩陣A的解為:

A=(XTX)-1XTZ

(10)

聯立式(5)可以求解出待估計參數ymax,xmax以及S。

依據此高斯擬合式,筆者擬合多組切片的磨損分析結果,復現三維磨損狀態。

1.4 軸承磨損有限元分析

1.4.1 磨損仿真分析流程

由于磨損是一個增量過程,一個完整的磨損周期仿真包括以下幾個步驟:

1)結合有限元理論,利用ABAQUS求解軸承滾子與內外圈的非線性接觸問題,獲得節點接觸力、相對位移和節點坐標等信息;

2)利用Archard磨損公式求解節點的偏移量,偏移方向為接觸點的法向,二者均通過UMESHMOTION用戶子程序[13,14]來實現,將磨損深度計算結果反映于節點的移動。

軸承內圈發生一定程度的磨損退化后,會改變內圈接觸表面的幾何形狀,為此,筆者采用ALE網格偏移技術,對軸承內圈磨損退化后的幾何形狀進行更新,如圖3所示。

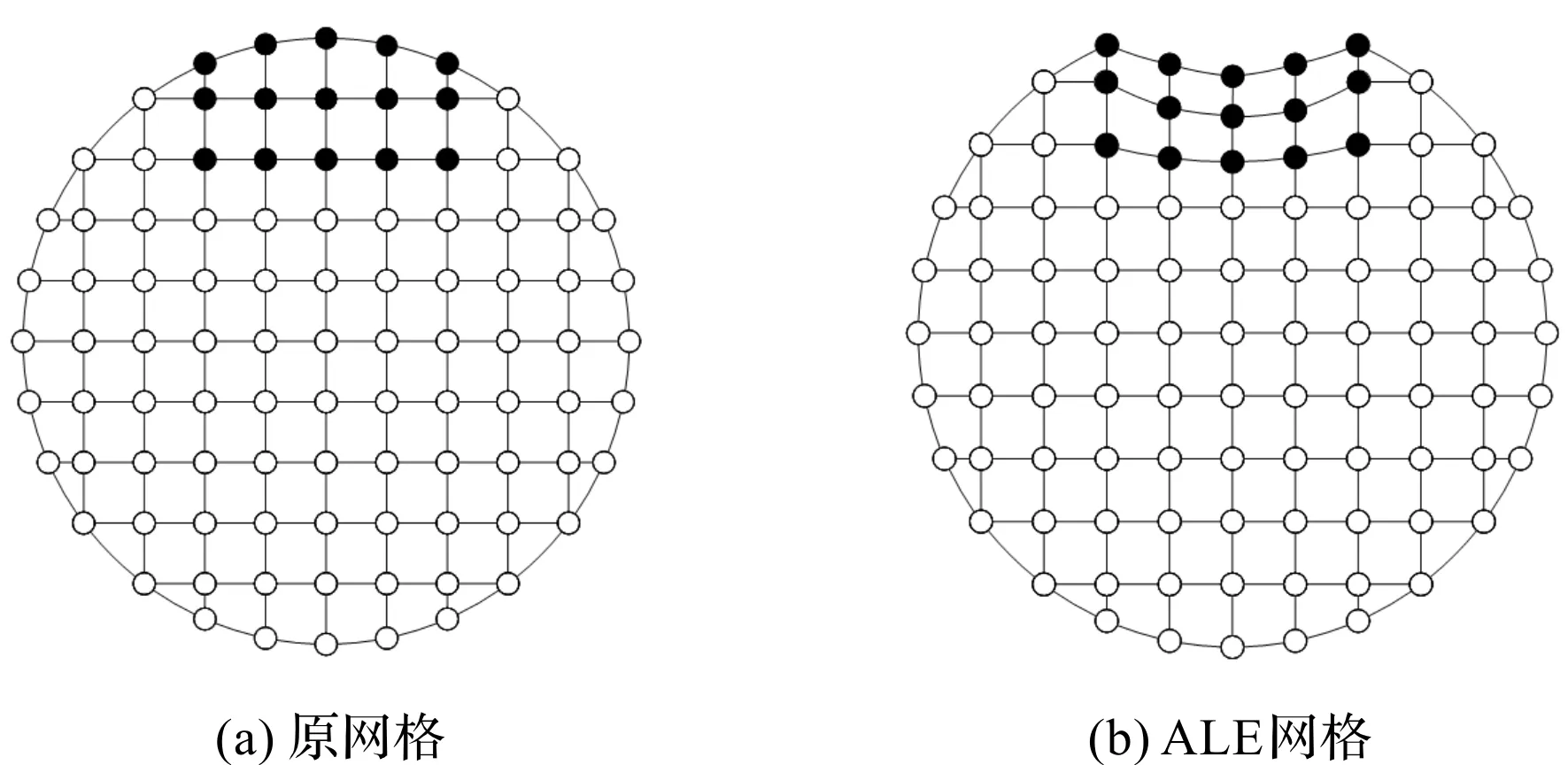
圖3 ALE網格自動偏移技術

在每個增量步開始時,筆者重新求解非線性接觸問題,同時計算該增量步下的磨損增量,不斷循環往復,直到完成全部增量步計算。

USESHMOTION磨損計算子程序使用Fortran語言編寫,在ABAQUS二次開發中實現。

據此得到磨損仿真分析具體流程,如圖4所示。

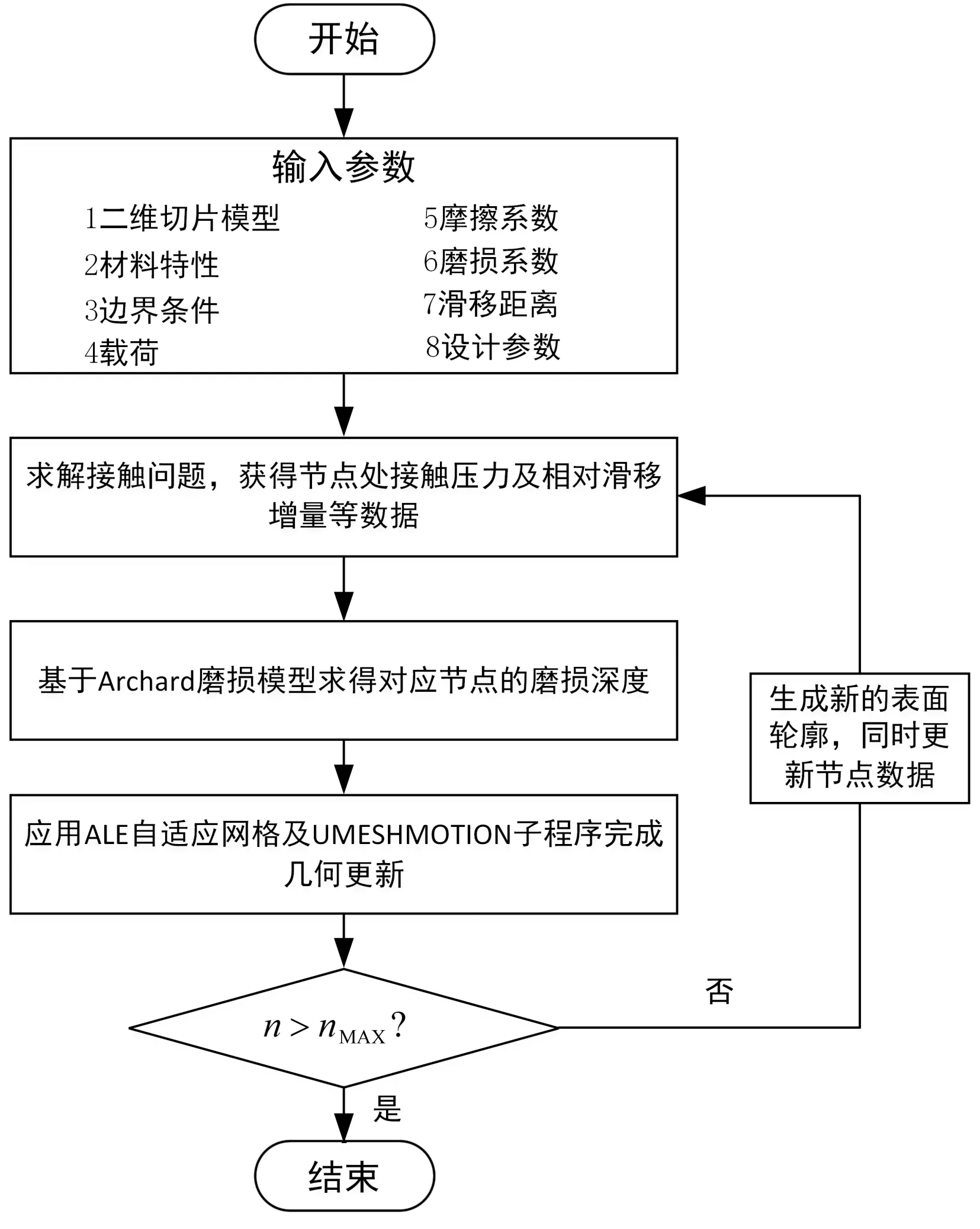
圖4 磨損流程圖

1.4.2 磨損有限元模型

接下來,筆者采用ABAQUS隱式方法對二維軸承切片磨損狀態進行分析。

為了便于計算收斂,筆者對整個加載過程進行了細化:1)內圈全部節點耦合在圓心處,在初始分析步中,僅放開沿y軸的垂向自由度;2)保持架全部節點耦合在圓心處,在初始分析步中,僅放開繞中心軸線的旋轉自由度;3)外圈始終添加全約束。

全程設置2個分析步step1至step2:step1在內圈耦合點添加垂向載荷25 000 N;step2放開內圈繞軸線轉動的自由度,同時添加內圈轉速1 000 r/min。滾子與內外圈的接觸形式采用表面與表面接觸,以滾子表面作為主面,內滾道外表面作為從面的接觸方式;在磨損分析之前,筆者對內圈磨損區域預設ALE網格自適應區域,考慮到網格單元的適用性,劃分時單元類型選擇CPS4(四節點雙線性平面應力四邊形單元),同時對滾子與內外滾道的邊緣區域進行網格細化處理。

構建的二維切片有限元模型如圖5所示。

各部件均設置為彈性材料。接觸面設置為表面與表面(surface to surface)接觸,接觸屬性分為切向和法向兩部分,切向行為采用靜摩擦-動摩擦指數衰減:靜摩擦系數為0.1,動摩擦指數為0.05,衰減指數為0.01;法向行為采用硬接觸。

由于模型尺寸較大,為了保證計算的可靠性,需先探討有限元模擬計算中軸承內部接觸狀態的網格有效性。筆者共設計5組網格數量,針對滾子及內外滾道采取不同程度的網格細化處理,以此來完成對網格有效性的驗證。

5組網格的具體劃分尺寸及數量如表2所示。

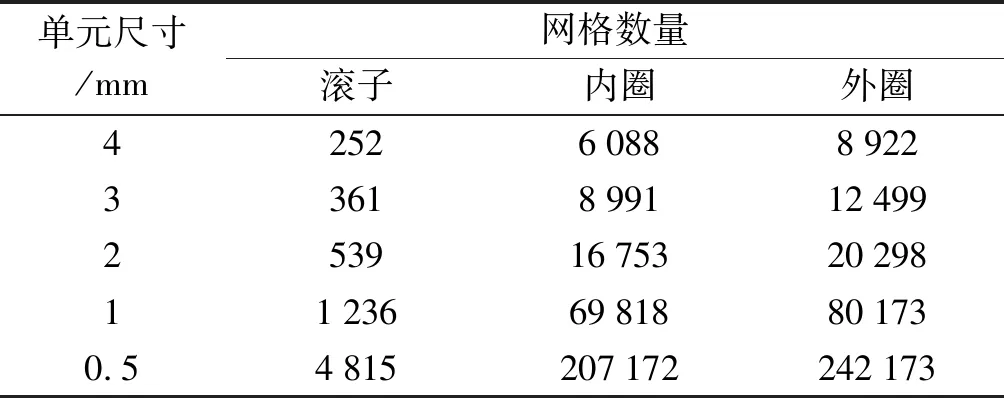
表2 網格具體參數

模擬進行0.1 s后,筆者觀察其模擬接觸力結果,如圖6所示。

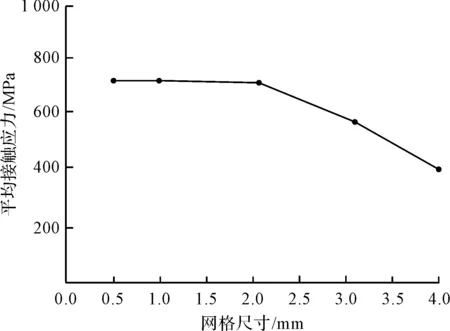
圖6 內滾道平均接觸應力

由表2及圖6可知:網格數量對有限元模擬仿真結果有較大影響,當網格劃分尺寸為2 mm時,此時網格數量為49 795,模擬結果開始趨于穩定。

依據上述分析,筆者選用尺寸為2 mm的網格對軸承接觸區域進行細化處理。

2 磨損結果分析與討論

2.1 方法有效性驗證

2.1.1 模型高效性與收斂性對比

不同切片數量會影響軸承內圈摩擦磨損分析的時間差異。

筆者以5為初始切片數量,對三維模型進行切片,并行研究數量為5片、10片、20片以及30片,共4組切片式來驗證半解耦分析法的計算效率,將計算結果與傳統三維磨損仿真分析的結果進行比較,并且將該對比實驗在同一臺計算機上執行(用于比較時間)。

在仿真時,筆者將2種軸承磨損損傷的分析方法均設置為105個增量步。切片計算結果的高斯擬合過程在MATLAB中完成。由于該擬合過程運行時間較短,筆者主要對比有限元分析完整過程的時間損耗。

相關計算結果,即磨損方法計算時間對比如表3所示。

表3 磨損方法計算時間對比

需要注意的是,在切片式半解耦損傷計算方法中,每一個二維切片模型的計算時長較為固定,通常在6.5 h～7.2 h之間,隨著切片數量的增加,相關模型的計算時間損耗呈現線性增長趨勢;當切片數量控制在30片以下時,半解耦損傷分析方法可以有效縮短仿真的時間損耗;若切片數量大于30,該方法的高效性難以體現。

由于磨損分析采用隱式分析步進行,在非線性條件下極易出現模型不收斂,導致仿真終止的現象(比如:欠約束、復雜接觸以及模型變形過大等,都可能使計算結果不收斂)。

筆者在確保材料屬性與邊界條件準確施加的前提下,討論切片式半解耦損傷分析方法與傳統三維分析方法的迭代收斂情況。

在計算中,迭代是在每個增量步中進行的。在一個增量步中,迭代的最高次數為16次,若在16次迭代中ABAQUS求得平衡解,就會進入下一個增量步,若未獲得平衡解,軟件將會減小當前增量步時間,繼續迭代;若增量步時間折減次數超過5次,則停止計算,同時當增量步總數超過設定的最大增量步數目時,停止計算。

此處,筆者設定了105個增量步,用于模擬軸承內圈的磨損損傷演化過程,歷史收斂圖(收斂情況對比分析)如圖7所示。

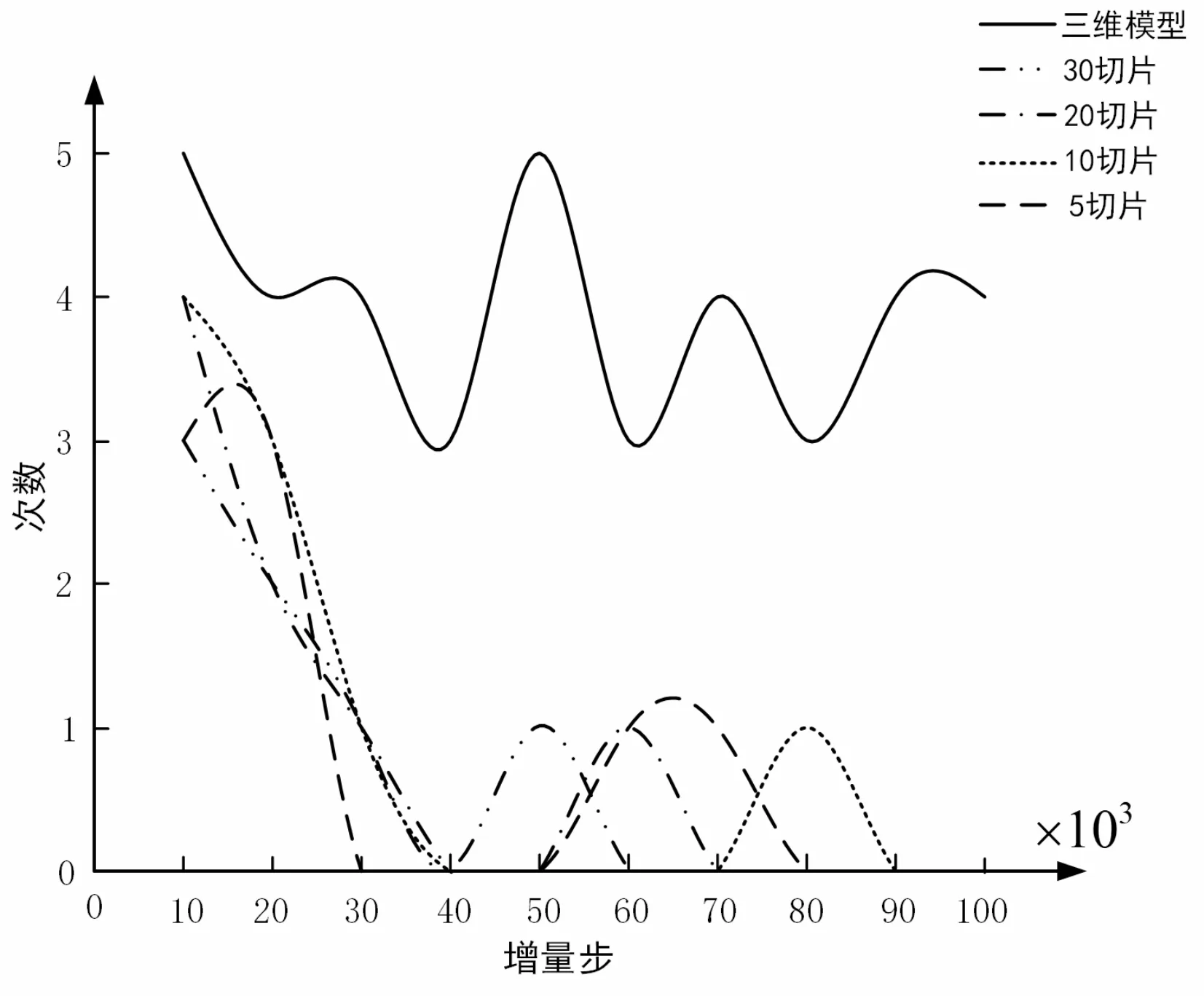
圖7 收斂情況對比分析

圖7為三維模型與多組切片式半耦合模型的收斂情況,圖中X軸表示對應的不同增量步,Y軸表示對應增量步下的最大連續迭代不收斂次數。

筆者分析圖7中曲線得到以下結論:

1)無論切片數量為多少,其對應的二維磨損模型的收斂情況均相似;在30 000個增量步之前,模型的最大連續不收斂次數呈下降趨勢;在連續計算40 000個增量步之后,切片模型的磨損分析會偶爾出現1次迭代不收斂;

2)與切片式半解耦損傷分析法相比,三維磨損模型的最大連續迭代不收斂次數非常不穩定,主要集中在3次～4次之間,該次數瀕臨模型計算的崩潰階段。

2.1.2 模型準確性驗證

驗證上述方法有效性的一般手段為將切片式半解耦損傷分析方法的結果與傳統的有限元分析結果進行比較。筆者將該方法與軸承三維有限元磨損仿真分析方法進行對比,對切片式半解耦磨損分析法的模擬結果進行了驗證。

傳統的三維建模包括軸承內外圈、滾動體及保持架四部分,建模時不考慮密封與倒油孔的影響;在三維磨損分析中,筆者同樣設置2個分析步(step1和step2),施加法向載荷25 000 N,添加轉速為1 000 r/min;接觸形式、增量步及邊界條件設置與上述一致。

為了方便探討三維磨損模型中的最大磨損深度,筆者在軸承內滾道處列出了檢測磨損增量的測點位置標識,如圖8所示。

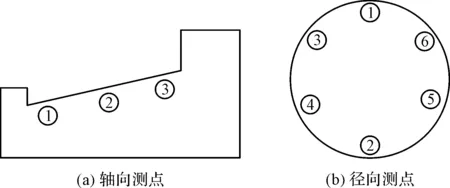
圖8 軸承內滾道磨損測點位置

隨著磨損仿真增量步的增加,磨損增量測點的深度也發生相應的變化。

在三維模型完成全部增量步計算后,筆者統計每個測點的磨損深度,得到的結果如表4所示。

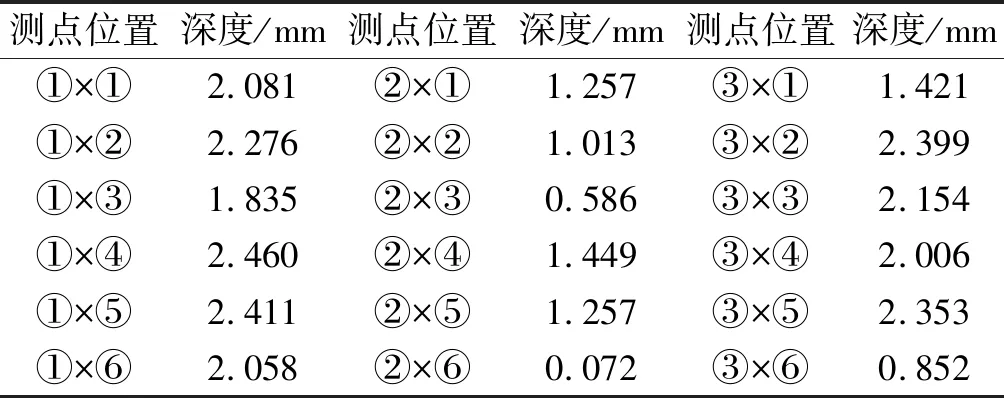
表4 對應測點磨損深度

通過分析表4中數據可知:在105個增量步仿真時長結束后,三維模型軸承內圈仿真計算的最大磨損深度為2.460 mm,最小磨損深度為0.072 mm。

筆者依舊采用切片數量為5片、10片、20片以及30片的半解耦分析方法的磨損計算結果與之進行比較。

相關磨損對比結果如表5所示。

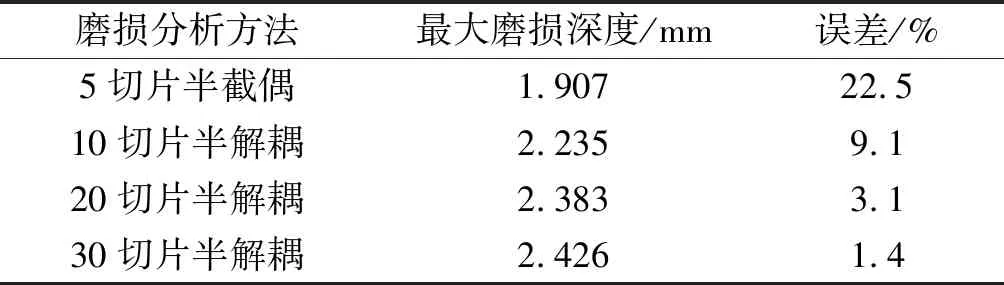
表5 磨損結果對比

分析表5可知:

5切片的二維模型的最大磨損深度擬合結果為1.907 mm,與三維模型的誤差達22.5%;當切片增加至10片時,誤差下降到10%以內,為9.1%,可信度提高;隨著切片數量的逐漸增加,仿真計算時間成本提升的同時,誤差也逐漸降低;當切片數量達30片時,擬合最大磨損深度為2.426 mm,誤差僅有1.4%,但此時該組耗時與三維模型接近。

2.2 磨損結果分析

根據上述分析結果,筆者提取20片切片的半解耦損傷仿真計算的接觸力及磨損深度等數據,以探討軸承內圈磨損情況。

軸承內圈接觸力情況,即軸箱軸承滾動體與內圈接觸應力曲線,如圖9所示。

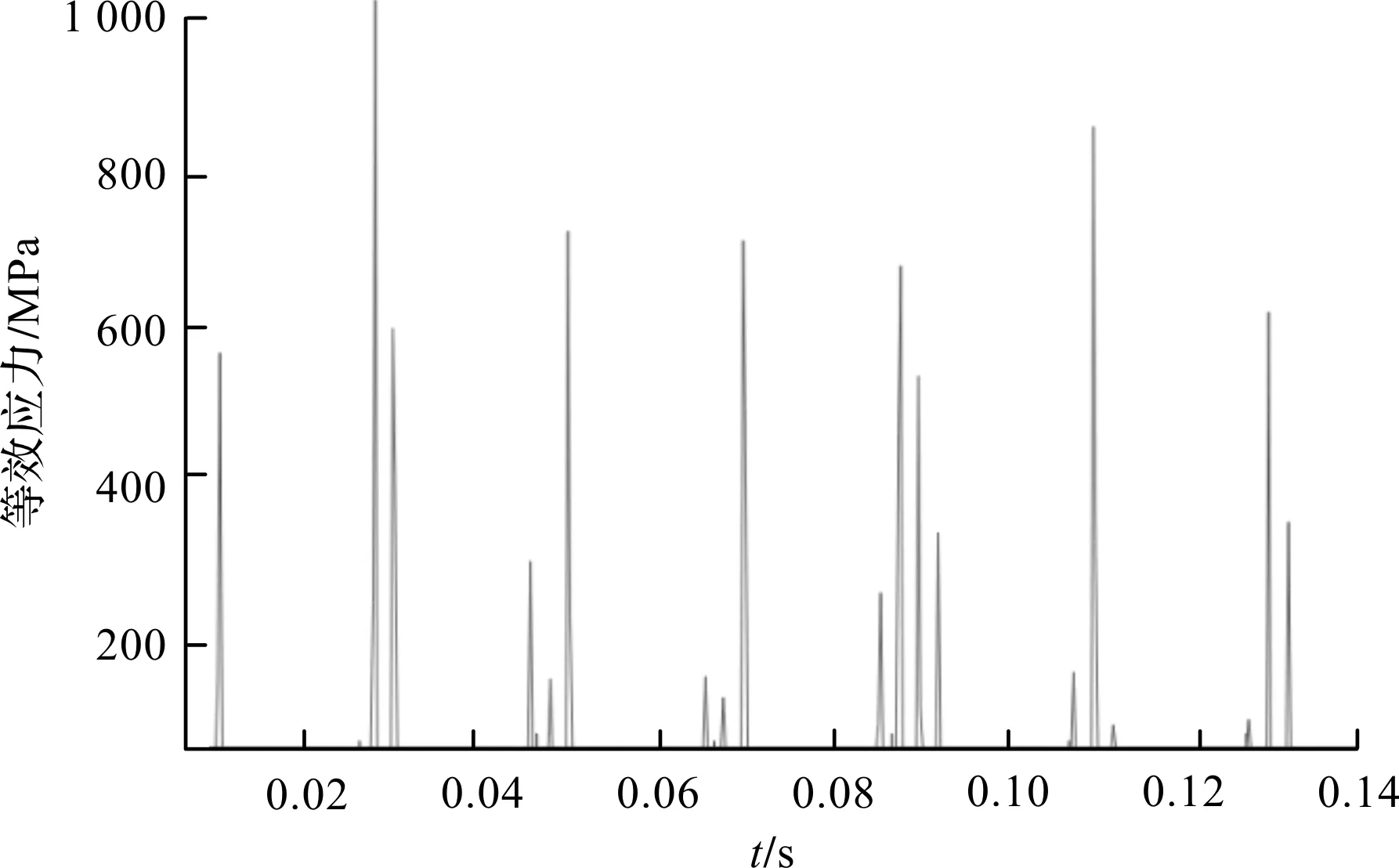
圖9 軸承內圈接觸壓力

圖9中,在滾子與內圈的接觸起點,據內圈中心的轉動角度為0度的接觸對中,處于承載區的滾動體由于徑向載荷作用受到來自軸承內外圈的擠壓作用,使得軸承內部徑向間隙減小至0,滾動體與內圈接觸連續且穩定,可以得出內圈接觸區域的平均接觸應力為703.2 MPa,然后其沿著滾動體中心線與內圈中心線夾角的增大而逐漸降低;當滾動體運動到非承載區時,滾動體所受內外圈作用力、振動及撞擊力較小且運動狀態較不穩定,內部徑向間隙較大,接觸并不完全,使得內圈非承載區接觸區域的接觸應力接近0 MPa。

利用二維擬合思路,筆者將軸承內圈不同位置節點對應的磨損量進行擬合,得到了軸承內圈磨損分布結果,如圖10所示。

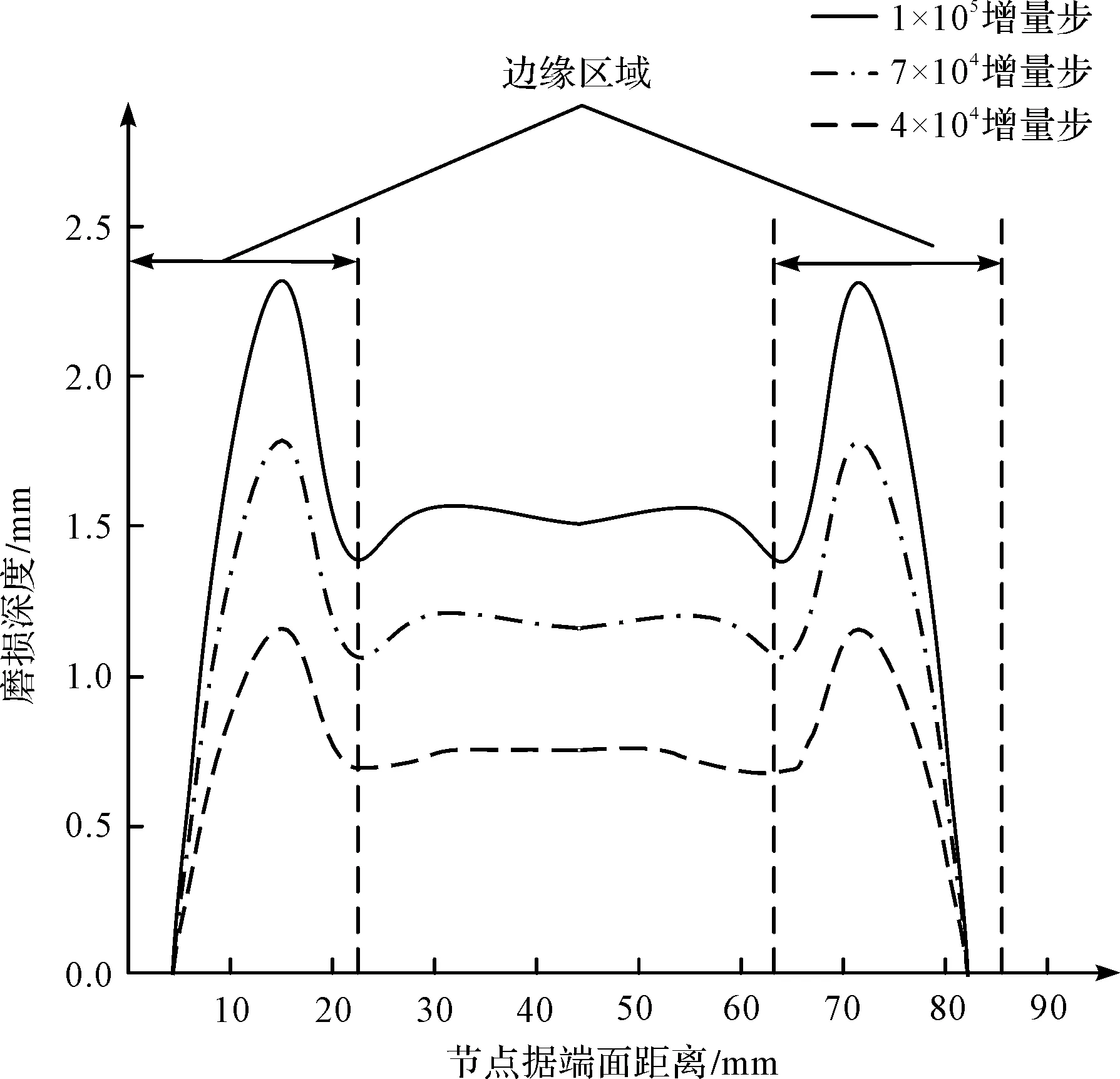
圖10 軸承內圈磨損分布

由圖10可知:由于邊緣壓膜效應[15],在接觸發生的邊緣區域產生應力集中現象,使得滾動體與內滾道接觸面的最大磨損深度出現在滾動體邊緣位置;而在內圈中心區域,由于滾子與內圈的接觸狀態穩定,磨損也較為平均;在105個增量步仿真結束后,內圈接觸邊緣區域的最大磨損深度達2.38 mm。

在接觸區域的中間位置,滾動體自轉運動狀態較穩定,接觸應力分布比較均勻,其平均磨損深度為1.44 mm。

軸承內滾道最大磨損深度變化,即隨著增量步的增加,軸承內圈最大磨損深度的變化情況,如圖11所示。

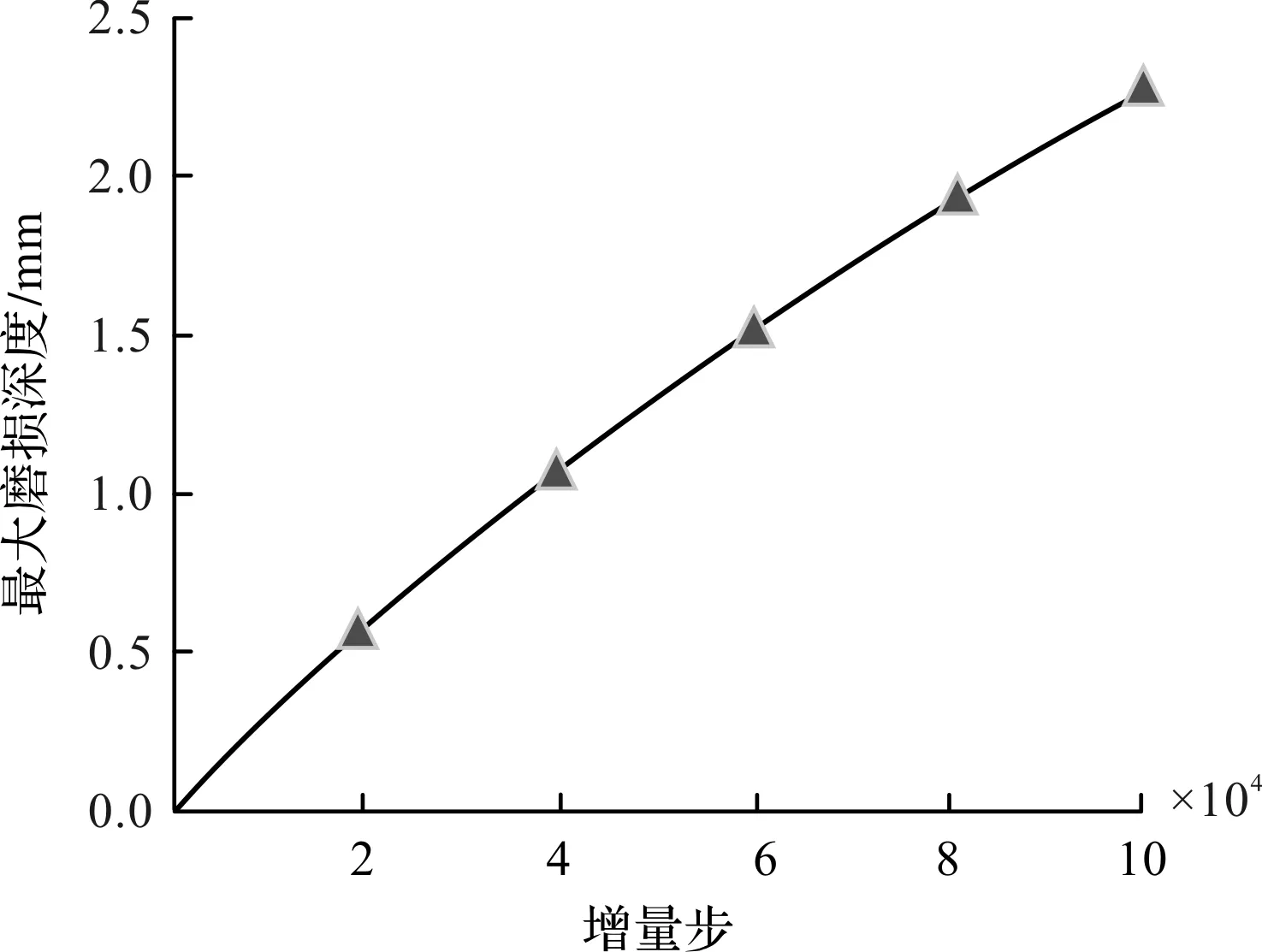
圖11 軸承內圈最大磨損量變化

圖11中,在磨損系數不變的情況下,磨損深度主要受接觸應力及接觸位移的影響[16]。

從圖11中曲線可以看出:最大磨損深度并非隨著軸承轉動增量步的增加而產生線性變化,其斜率(磨損率)隨著磨損循環次數的增加而逐漸減小;導致軸承內圈最大磨損深度非線性增加的重要因素是隨著磨損深度的增加使得內部徑向間隙增大,其直接造成了內圈接觸區域的接觸應力非線性變化[17,18]。

3 結束語

筆者以轉向架軸箱軸承為研究對象,基于數值模擬的方式,提出了一種切片式半解耦磨損分析方法,構建了多組軸承內圈磨損損傷的二維有限元仿真模型,并在給定工況下,對該軸承內圈的磨損狀態進行了模擬及結果擬合,最終得到如下結論:

1)筆者使用切片式半解耦磨損損傷分析法、高斯擬合以及ABAQUS中強大的ALE網格偏移及UMESHMOTION子程序技術,其可替代三維模型磨損分析方法,在保證誤差在10%以下的同時,該模型的計算效率比三維模型提高了約3倍。針對轉向架軸箱軸承及其他結構尺寸較大、仿真分析時間較長的模擬模型,該方法不失為一種高效的仿真研究方法;

2)研究發現,軸承內圈表面磨損最為嚴重的地方出現在滾動體與內滾道接觸的邊緣區域,而接觸的中心區域磨損程度較輕(由于其接觸狀態穩定)。同時,內圈最大磨損深度并不是隨著增量步的變化而線性增加,這是由于軸承的磨損致使部件間隙發生變化,導致滾動體與內圈接觸應力發生非線性變化。

目前,筆者僅對軸承內圈的磨損損傷進行了數值模擬分析。在后續研究中,筆者將開展其他零部件磨損損傷研究,以進一步了解軸承的磨損特性,同時也擬通過實驗,對磨損的數值模擬結果進行驗證。