基于尺度律的輕量化協作機器人關節傳動系統優化選型*

林家春,蘇 浩,員若男

(1.北京工業大學 材料與制造學部,北京 100124;2.北京市精密測控技術與儀器工程技術研究中心,北京 100124)

0 引 言

隨著協作機器人得到廣泛應用,人們對機器人技術也在不斷提出新要求。新一代的協作機器人應具有高效率、高功率密度比、輕量化等特點[1],尤其是在移動和可穿戴機器人(例如外骨骼)領域,高效率和低重量至關重要。

協作機器人關節是協作機器人總重量的主要來源[2],其核心部分是由電機和諧波減速器組成的傳動系統,決定整個關節的重量和性能[3]。因此,從源頭出發,實現關節輕量化設計的關鍵是對電機和減速器進行優化選型。

傳統的電機和減速器的選型通常采用順序法,即根據負載特性,從備選目錄中選擇減速器和電機[4]。傳動比選擇的原則是在滿足性能要求的前提下,盡可能降低電機尺寸,以節約成本。這種方法由于需要從初始選擇開始,在所有可能的組合中進行枚舉或試錯,需要耗費大量時間才能找到合適的組合,因此其效率非常低下;并且該方法也不能保證探索所有可能的解決方案,其會導致解決方案過大或者次優,從而不能找到最佳的電機和減速器的組合[5]。

針對機電系統電機和減速器的優化選型問題,國內外學者提出了多種解決辦法。

PASCH KA等人[6]引入了慣量匹配的概念,并在理想條件下,將其用于選擇負載加速度最大的傳動比。VAN D S H J等人[7,8]通過將扭矩、速度和傳動比進行了標準化處理,解決了傳動系統的設計問題。ROOS F[9]建立了電機和減速器的數據庫,并從中提取了選型參數(如尺寸、重量),設計人員可以根據不同的設計需求對數據庫中的信息進行篩選,最終得到滿足要求的組合。ZHOU L[10]在傳動系統建模過程中,考慮了電機和減速器的特性,包括傳動比、齒輪慣量、電機慣量和齒輪效率等,對輕量化機器人機械臂傳動鏈進行了優化設計。CUSIMANO G[11]在純慣性負載的情況下,通過計算符合重量最小化所需連續扭矩最佳齒輪比的方法,以此來選擇合適的電機和減速器。MEONI F[12]提出了機電伺服軸模型,該模型從商業手冊中提取了數據,對影響電機和減速器運行的參數進行了數據擬合,在此基礎上提出了一種連續優化程序,采用該程序可以找到各種目標函數的最佳電機和減速器組合。RICHIEDEI D等人[13]提出了一種基于尺度律的方法,該方法改進了最佳齒輪比的概念,采用尺度律說明了電機、減速器和傳動比之間的主要關系,最終得到了電機和減速器的最佳組合。

以上文獻中提到的優化方法大都是用于對機器人關節傳動系統的傳動比進行優化,但在優化過程中,同時考慮重量、尺寸的研究并不多見。

近年來,優化設計已經成為加快協作機器人產品上市的重要途徑[14]。因此,筆者以實現協作機器人關節的輕量化設計為目標,提出一種基于尺度律的優化選型方法。

首先,建立傳動系統的動態模型,構建以減速器和電機重量最小化為目標的優化函數;其次,構建尺度律模型將傳動系統所涉及的相關特性參數簡化,并通過所建立的電機和減速器的數據庫,對尺度律模型的正確性進行驗證;最后,采用具體選型實例對該方法的有效性進行驗證。

1 傳動系統特性及要求

1.1 關節傳動系統建模

一個通用的伺服傳動系統模型可以通過伺服電機、傳動裝置和負載三個關鍵要素來表示[15]。

傳動系統模型如圖1所示。

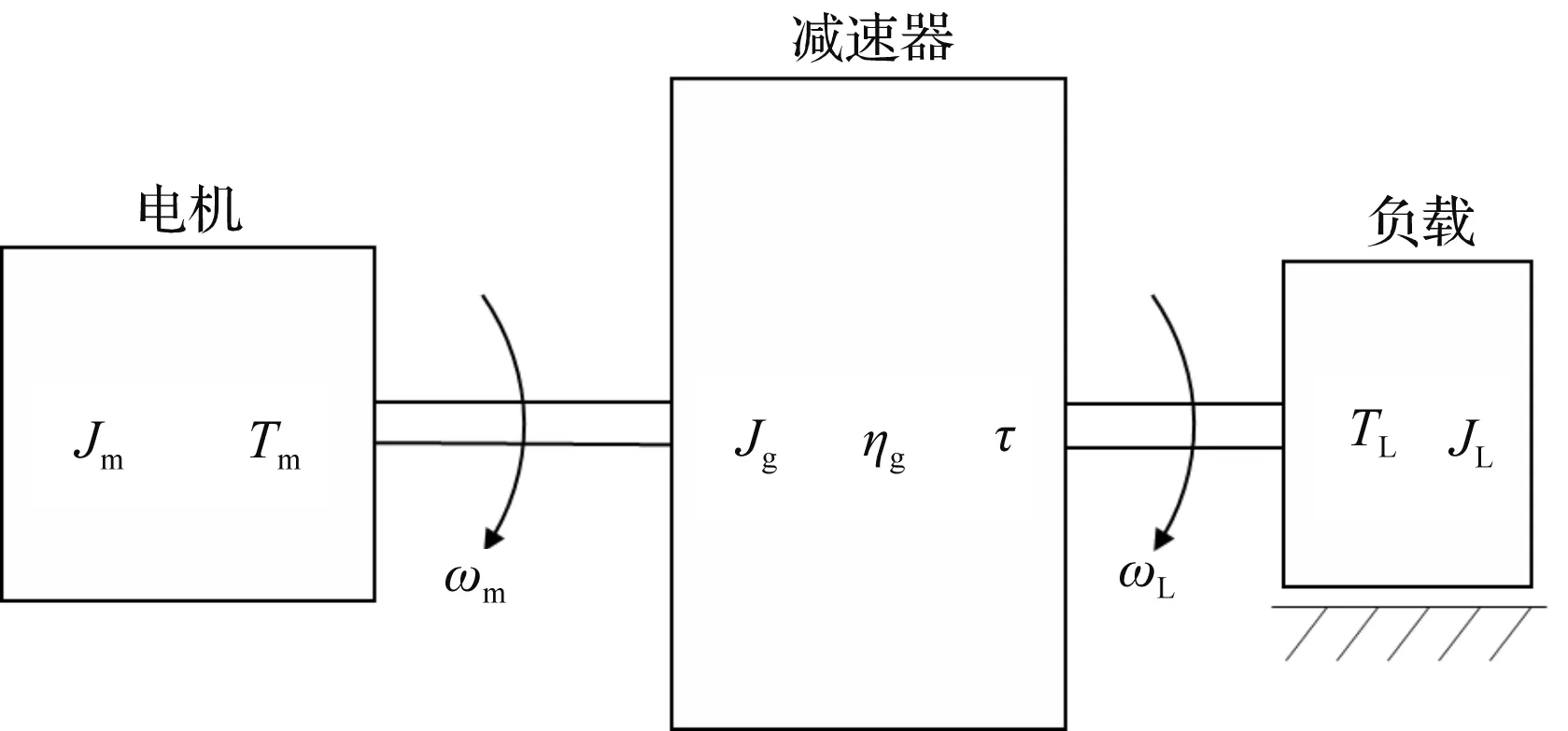
圖1 傳動系統模型

該模型可以代表多種機電系統,具有普遍適用性。協作機器人關節也可以用該模型進行表示。

筆者將圖1中的伺服傳動系統的動態模型寫成扭矩平衡方程。在恒定的負載條件下,電機驅動指定負載所需的電機扭矩Tm(t)為:

(1)

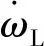
其中:

(2)

式中:ηd為機械效率;ηr為正向的機械效率。

考慮機械效率不同的流動方向對伺服驅動系統的選擇十分重要[13]。TL是由負載慣性轉矩、黏性摩擦力和外部扭矩組成的合力,其計算公式如下:

(3)

式中:Te為負載扭矩;JL為負載的轉動慣量;kf為黏性摩擦系數;ωL為負載的轉速。

負載的特性在進行選型之前是已知的,它取決于負載的運動曲線。通過將負載的運動曲線和這些模型用于表示傳動裝置和負載之間外部扭矩,可計算得到TL。

根據式(1)可知,驅動給定負載所需的電機扭矩取決于負載、電機和減速器的慣量。

1.2 電機選擇標準

協作機器人關節電機通常采用永磁同步電機(perma-nent magnet synchronous motor, PMSM)。為了保證電機能夠驅動負載,電機的選擇必須滿足如下三個條件。

電機在運轉過程中由于黏性摩擦、鐵損和磁滯產生熱量,且電機溫度會隨速度增加而增加[16],為防止電機過熱,一個周期T內所需電機轉矩的均方根值(RMS)應小于等于電機的連續轉矩,表示如下:

Tm,rated≥Tm,rms

(4)

其中:

(5)

將式(1)、式(5)結合,可以得到電機額定轉矩的約束條件為:

(6)

負載曲線的最大扭矩值必須小于或等于電機的額定扭矩值:

Tm,peak≥Tm,max

(7)

其中:

(8)

電機的最大轉速必須高于負載曲線所需的最大速度:

ωm,max≥ωL,max

(9)

式(4)、式(7)、式(9)表示伺服驅動系統中的任何電機選擇時必須滿足的約束條件。

1.3 減速器選擇標準

伺服驅動系統應用經常使用三種減速器:傳統齒輪副、行星齒輪系和諧波傳動[17]。諧波減速器憑借其傳動比范圍大、承載能力強、運動精度高等優點被廣泛應用于協作機器人關節中。

在選擇諧波減速器時,通常需要考慮以下三個條件:

Tg,rated>TL,maxfs

(10)

安全系數fs具體選擇數值由協作機器人實際應用領域和每小時的工作循環數決定,通常有:

fs>1.4

(11)

減速器的額定扭矩要大于負載的平均扭矩,即:

Tg,rated>TL,Rmc

(12)

諧波減速器通常使用TL,Rmc值來計算額定扭矩,該值是對諧波減速器結構部件累計疲勞的量度[18],故其數值與減速器的壽命有關。其計算標準已經用于機器人應用中,其中TL,Rmc的計算公式如下:

(13)

假定電機能驅動給定負載,在滿足以上減速器的選擇條件下,允許的最大傳動比為:

(14)

式(10)、式(12)和式(14)表示了伺服驅動系統中任何減速器選擇時必須滿足的條件。

橫縱比能反映出電機和減速器對關節尺寸的影響,反映機器人關節的扁平程度。為防止選型得到的關節形狀與實際不符,筆者根據協作機器人關節實際應用對橫縱比進行約束,表示如下:

(15)

式中:lm為電機長度;dg為減速器直徑

以上電機和減速器的選擇條件具有普遍性,適用于任何傳動系統選型。

1.4 目標函數優化

優化目標是在滿足驅動負載性能要求的基礎上,從建立的電機和減速器數據庫中找到重量最輕的組合。因此,筆者將目標函數f(x)定義為電機重量mm和減速器重量mg的總和,可表示為:

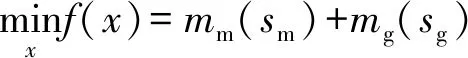
(16)

式中:變量x為數據庫中所有滿足驅動負載條件的電機sm和減速器sg的組合。

從式(16)可知,優化函數涉及眾多參數。

為了能清晰、快速有效地找到滿足優化目標的電機和減速器的組合,方程式中涉及的參數必須減少。為解決該問題,筆者采用尺度律對傳動系統的每個組件重新建模,將涉及多個參數的優化目標函數減少為僅由2個參數表示:電機堵轉轉矩Tstall和減速比τ。

2 尺度律及其應用

2.1 尺度律介紹

尺度律(也稱相似律),是表示兩個相互聯系的物理量之間的函數關系的尺度律模型[19]。尺度律被應用于許多不同領域,如微系統、力學、液壓、流體力學等,其被用來確定或調整系統的尺寸,評估系列化產品的開發成本[20]。

在設計問題中使用尺度律是非常有利的,因為它大大減少了某些物理量所涉及的參數數量,從而避免出現由于物理量的模型過于復雜而導致系統無法使用[4]的情況。許多文獻中使用尺度律對機電一體化產品進行分析設計與優化,并應用于機器人系統、電機、無人機等設備中。

尺度律是代數模型,通常采用冪指數的形式:

(17)

y*與x*的計算分別為:

(18)

式中:y為所研究的參數;xi為組成研究參數中具有代表性的獨立性參數;i為參數的數量;xref,yref為假定的參考值[21]。

筆者采用尺度律,將電機和減速器的參數表示為其尺寸的參數的模型。這些模型用于表示τ、Tstall與Jm、mm、Tg,rated、mg、Jg之間的關系。

尺度律模型的評估和驗證的主要數據來源是電機和減速器廠家目錄中的技術參數數據,并使用最小二乘法擬合來獲得尺度律模型參數。文中所提出的尺度律模型對任何其他幾何形狀仍然有效。

2.2 電機尺度律

2.2.1 電機轉動慣量尺度律模型

文獻[21]指出,電機的堵轉轉矩的計算公式為:

(19)

式中:C為電機的利用率;lm為電機長度;rm為電機半徑。

電機轉動慣量的計算公式為:

(20)

式中:ρm為電機密度;τ為減速比。

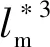
(21)

為了驗證該尺度律模型的準確性,筆者采用最小二乘法對2個參數進行擬合,參數數據來自建立的電機數據庫。擬合結果如圖2所示。

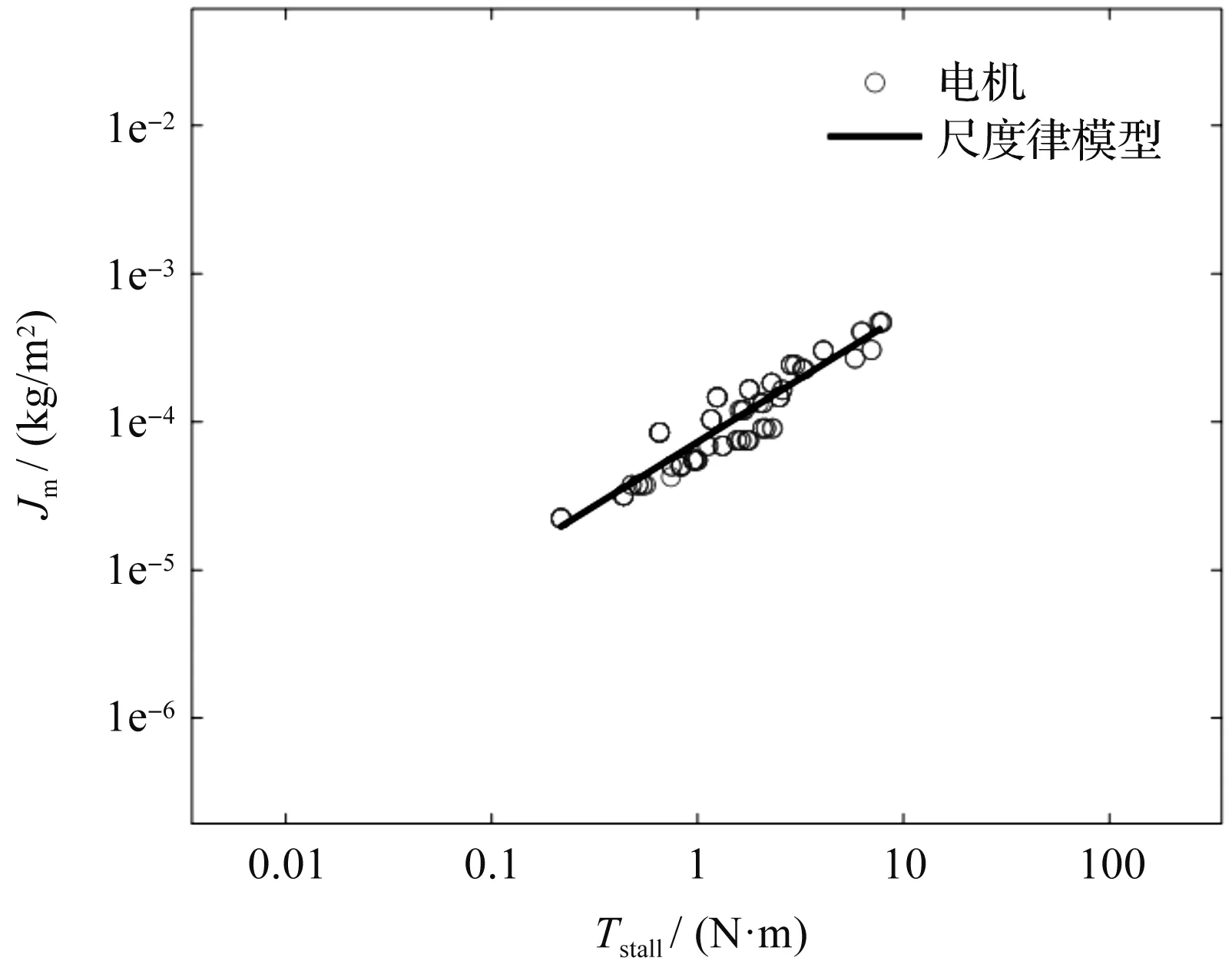
圖2 電機轉動慣量的尺度律模型與實際數據對比

圖2中:黑線是根據尺度律模型擬合得到的值,圓圈是從數據庫中得到的電機數據。

式(21)中am是最小二乘法擬合電機數據得到的系數值。從擬合的結果中可以看出,實際數據點與所提出的尺度律幾乎是一致的,從而驗證了該尺度律模型的準確性。

2.2.2 電機重量尺度律模型

文獻[16]得出了電機的額定轉矩與轉子半徑和長度的關系式:

(22)

式中:Cm為在特定的電機類型和相同的冷卻條件下的恒定常數值。

而電機重量的計算為:

(23)

mm=anTm,rated

(24)

式中:an為擬合得到的系數值。

同樣,筆者采用最小二乘法對該模型進行擬合驗證,擬合結果如圖3所示。

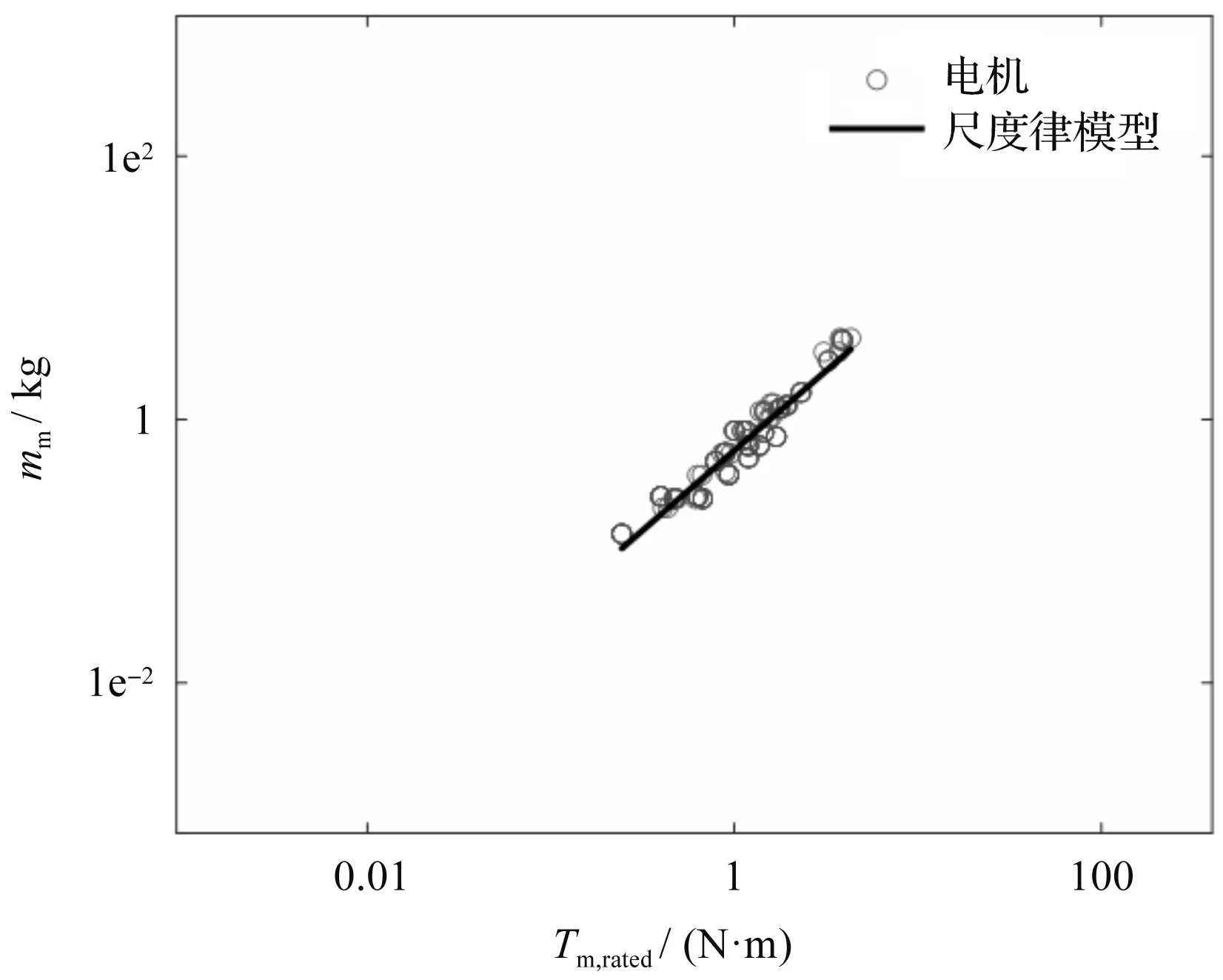
圖3 電機重量的尺度律模型和實際數據對比

2.3 減速器尺度律

2.3.1 減速器重量與轉動慣量尺度律模型

對于減速器重量與轉動慣量的尺度律模型,同樣是筆者將減速器的幾何尺寸與其相關的不同參數聯系起來得到的[22],表示如下:

(25)

mg=ahTg,rated

(26)

擬合驗證的結果如下。

減速器轉動慣量的尺度律模型與實際數據對比如圖4所示。

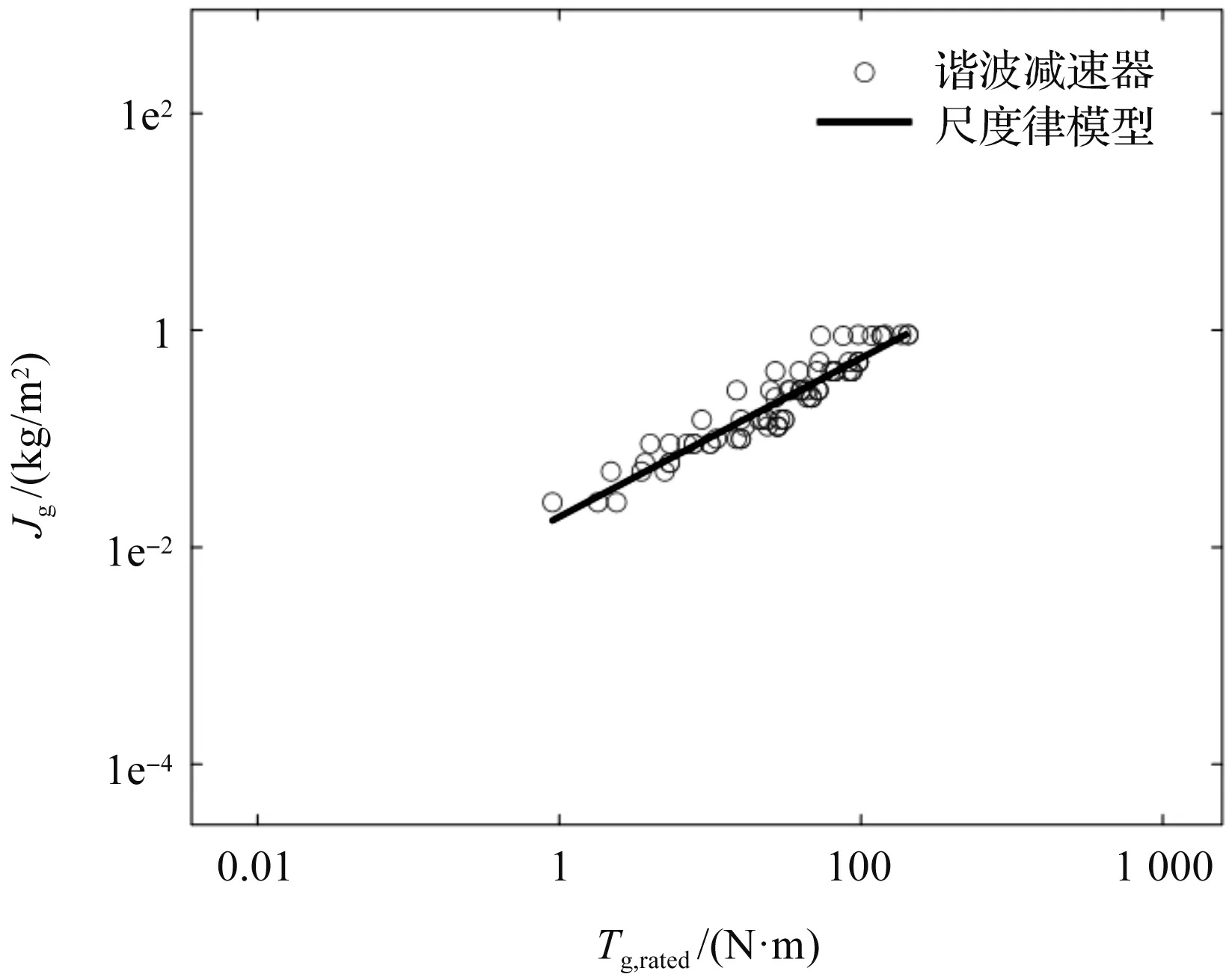
圖4 減速器轉動慣量的尺度律模型與實際數據對比

減速器重量的尺度律模型和實際數據對比如圖5所示。

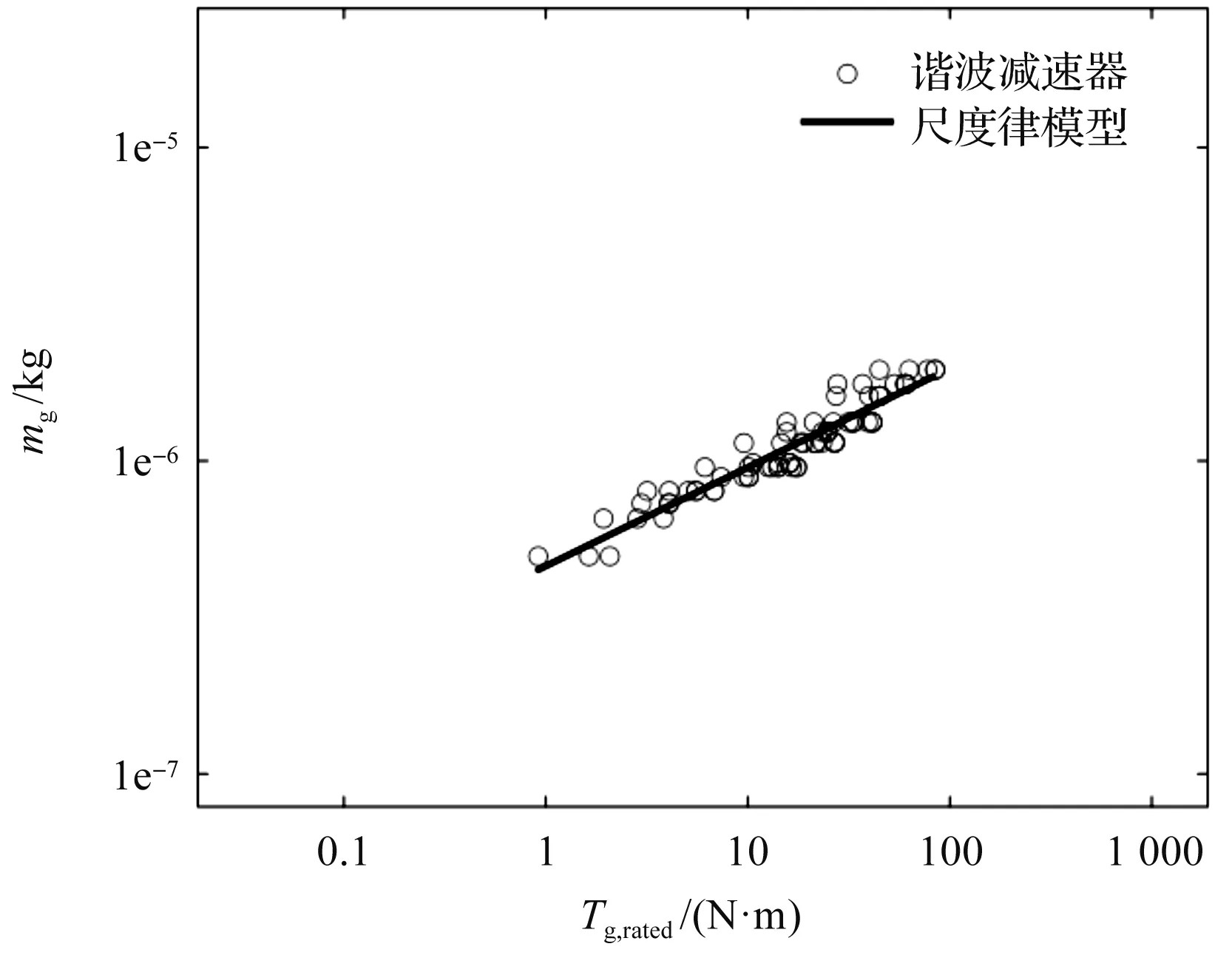
圖5 減速器重量的尺度律模型和實際數據對比

2.3.2 減速器減速比尺度律模型

由式(25)可知,減速器的轉動慣量可以通過其額定轉矩近似表示。文獻[5,13]提出,減速器的轉動慣量與減速比具有相關性,如果對具有近似相等額定轉矩的減速器進行縮放,可以得到減速比與轉動慣量的尺度律模型如下:

Jg=arτ-1

(27)

擬合驗證結果如圖6所示。

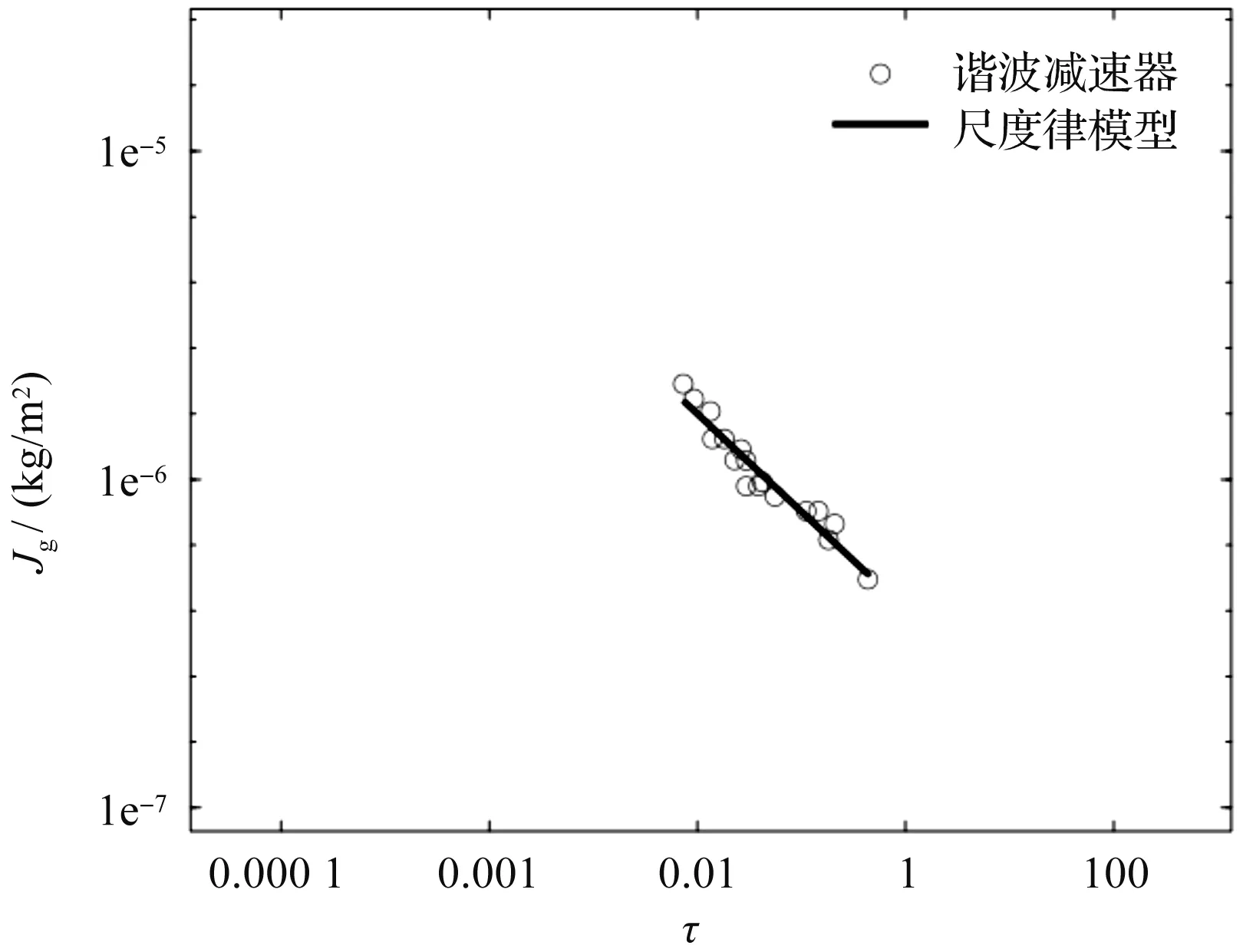
圖6 減速比的尺度律模型和實際數據對比

3 系統選型程序

3.1 優化函數簡化

根據第2節的尺度律可知,電機的重量為mm∝Tm,rated,減速器的重量為mm∝Tg,rated。因此可以將目標函數改寫為:

(28)

而對于電機的額定轉矩值,由式(4)可知,其可以由電機轉矩的均方根值表示:

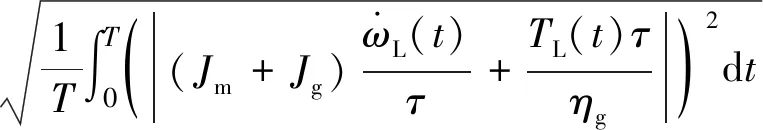
(29)

同時,由式(25)、式(27)可知,減速器額定轉矩又可以表示為:

(30)

最終,筆者將電機、減速器的尺度律模型代入,得到簡化后的目標函數為:

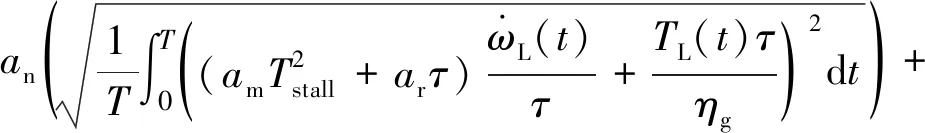
(31)

式中:an、am、ar、ah、ag都已知,其數值均為通過最小二乘法擬合后得到的系數值。

分析式(31)可知,關節傳動系統總重量的優化函數在簡化后僅與電機的堵轉轉矩Tstall和減速比τ有關。

3.2 系統選型程序

筆者針對協作機器人關節傳動系統的選型提出了一種基于尺度律的方法,以實現關節的輕量化設計為目標,選擇電機和減速器的最小重量組合。其步驟如下:

2)根據1.2節和1.3節提出的選擇標準,在數據庫中選擇合適的電機和減速器;

3)對從數據庫中得到符合條件的電機和減速器,根據第2節建立的模型,利用最小二乘法進行數據擬合,從而得到尺度律常數;

4)建立電機和減速器組合的最小重量為目標的優化函數,并將尺度律代入,將其簡化為僅由電機堵轉轉矩Tstall和減速比τ組成的函數;

5)將滿足驅動負載條件的電機和減速器數據代入優化函數中進行計算,根據計算結果確定電機和減速器的實際選擇型號。

4 選型實例和試驗

為了證明該方法的有效性,筆者選取了市面上兩款不同廠家(A和B)不同型號的協作機器人關節(各關節性能參數數據均來自于廠商官網),在相同的設計指標的條件下,采用基于尺度律的方法進行選型計算,將得到的結果與兩款關節的實際重量進行比較。

該方法是用于對協作機器人關節的電機和減速器進行選擇,通常電機和減速器的重量占關節總重量的70%左右。

兩款關節的廠家及型號如表1所示。

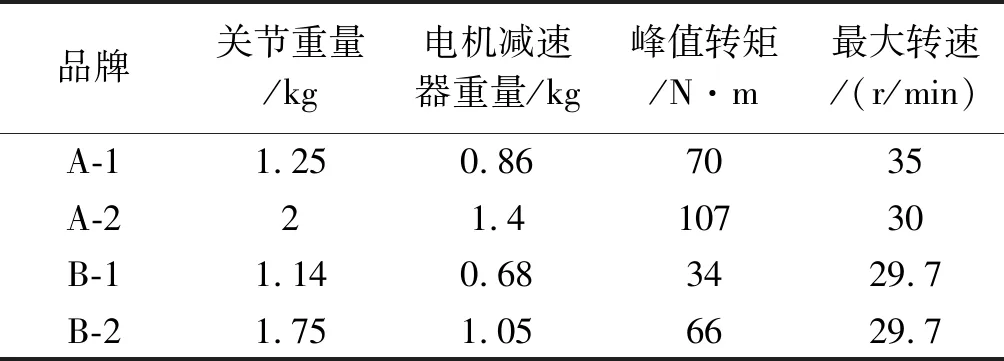
表1 A和B兩款關節的型號和性能參數

4.1 選型實例

對于A-1型號的關節,筆者將設計指標代入到優化函數中,得到了A-1性能指標選型結果,如圖7所示。

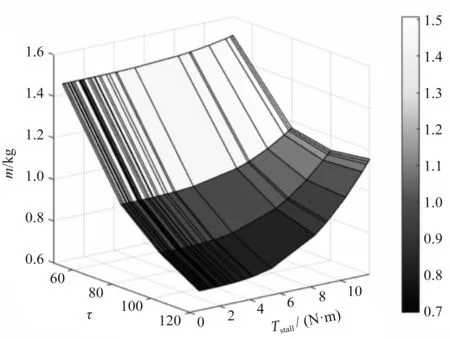
圖7 A-1性能指標選型結果

電機和減速器組合最小重量為0.7 kg,減速比τ=120,Tstall=0.6。

因此,筆者選擇的電機型號為TBSM85-07B40,重量為0.26 kg;減速器的型號為CSD-32-120,重量為0.51 kg。實際電機和減速器總重量為0.77 kg,實際結果與基于尺度律的模型的預測結果緊密匹配,從而進一步驗證了該方法的準確性。

同時,通過優化選型得到的結果與原始的設計重量0.86 kg相比,重量減輕了約7%。

A-2型號的性能指標選型結果如圖8所示。

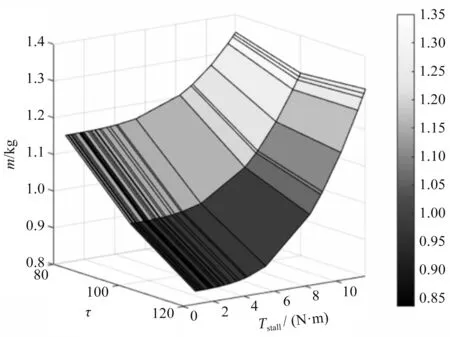
圖8 A-2性能指標選型結果

電機和減速器組合最小重量為0.83 kg,減速比τ=120,Tstall=1.13。

筆者實際選擇的電機的型號為TBM6051-A,重量為0.55 kg;減速器的型號為CSF-25-120,重量為0.51 kg。實際電機和減速器的總重量為1.06 kg,相較于原來的設計,重量減輕了約30%。

對于B廠家而言,兩個型號的關節選型結果如下:

B-1性能指標選型結果如圖9所示。

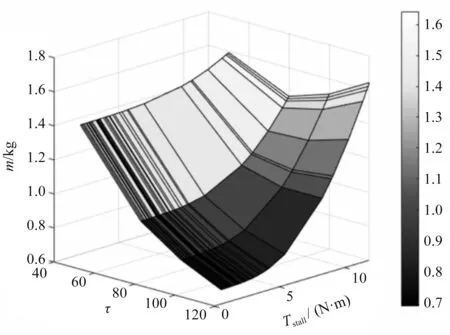
圖9 B-1性能指標選型結果

B-2性能指標選型結果如圖10所示。

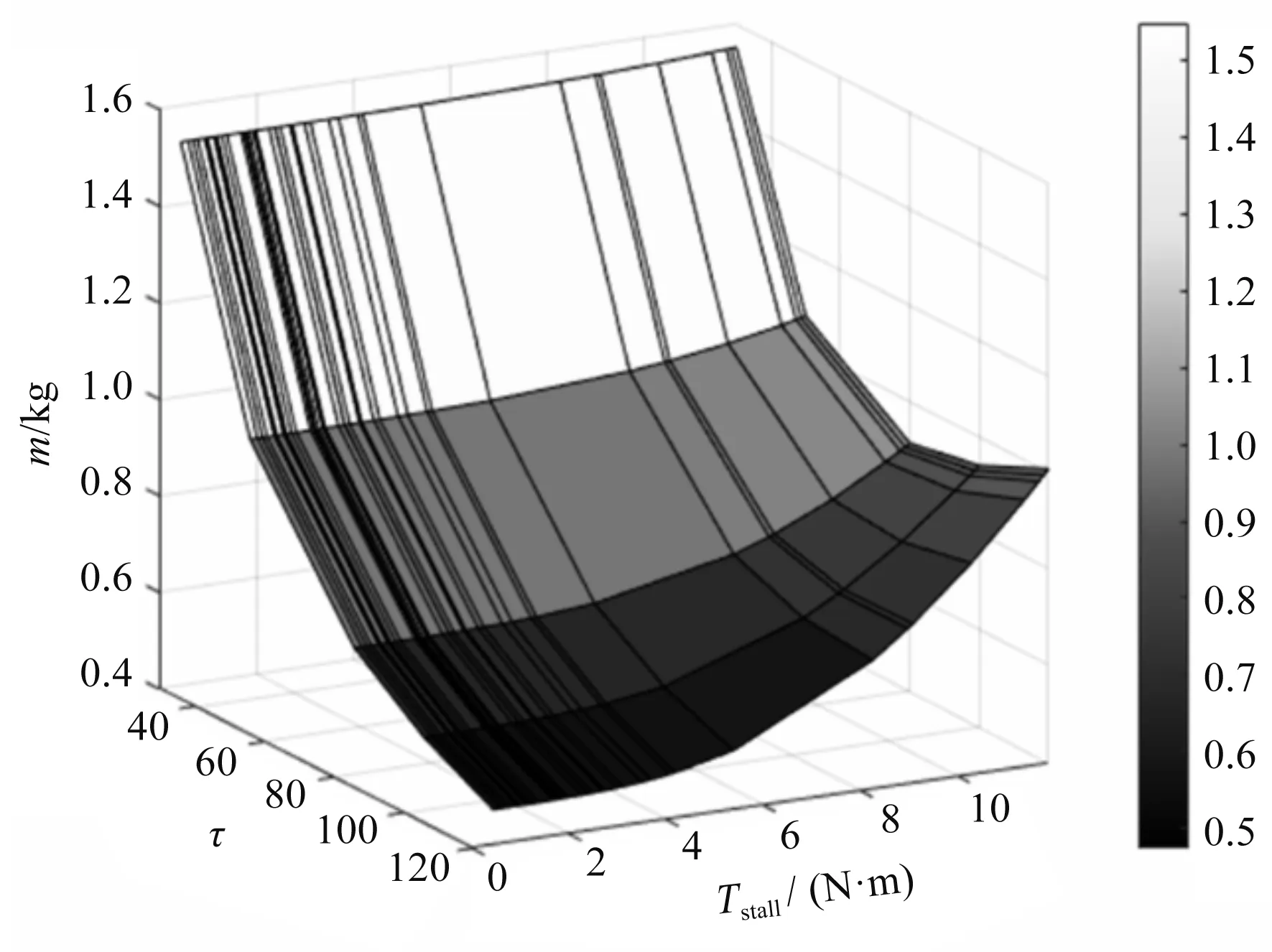
圖10 B-2性能指標選型結果

其選型得到的組合重量都比原設計重量減少了約20%～30%,從而驗證了該方法的有效性。

4.2 選型試驗

為進一步驗證該選型方法的有效性,參照科爾摩根(Koll morgen)的RGM17-100協作機器人關節模組,筆者進行了電機和諧波減速器的選型,并完成了關節模組設計。

關節模組性能參數表如表2所示。

表2 關節模組性能參數

根據基于尺度律的優化選型方法,依照表2所示性能參數,筆者進行了關節模組電機和諧波減速器選型.選型結果為:電機型號為河北宇捷TBSM76-15A31,重量為0.5 kg.

關節模組用無框力矩電機實物如圖11所示。

圖11 關節模組用無框力矩電機

諧波減速器型號為LHSG-III-17-100,重量為0.8 kg,其實物圖如圖12所示。

圖12 關節模組用諧波減速器

筆者設計的關節模組與科爾摩根RGM17-100電機和減速器重量對比結果,如表3所示。

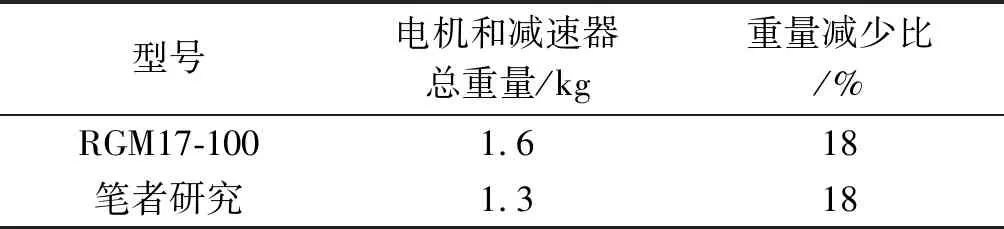
表3 選型結果與RGM17-100對比

由表3可知:相較于原始設計,使用基于尺度律的選型方法得到的電機和減速器總重量減少了約18%,驗證了該方法可以有效地減少電機和減速器總重量。

筆者在完成關節模組其他部件的設計選型后,最終完成了關節模組的設計。

關節模組的實物圖如圖13所示。

圖13 關節模組實物圖

5 結束語

為了實現協作機器人的輕量化設計目標,筆者提出了一種基于尺度律的協作機器人關節傳動系統優化選型方法。具體選型步驟如下:

1)建立協作機器人關節傳動系統的動態模型,根據模型確立了電機和減速器的選擇條件;2)建立以電機和減速器重量最小化為目標的優化函數,并使用尺度律對優化函數進行簡化;3)通過仿真實驗和實際試驗,對該方法的有效性進行驗證。根據選型結果,最終完成了關節的設計任務。

研究結果表明:

1)在仿真實驗中,筆者使用該方法對市面上銷售的4款關節的性能參數進行了選型,選型得到的電機和減速器的總重量比關節的原始設計減輕了20%,驗證了該選型方法的有效性;

2)在實際試驗中,筆者參照科爾摩根的RGM17-100關節的性能參數,使用該選型方法得到了電機和減速器的重量,其比原始設計的重量減輕了18%,從而進一步驗證了該選型方法的有效性。

在后續的研究工作中,筆者將會使用基于尺度律的選型方法進行不同關節性能參數的實際試驗,以進一步提高選型方法的可靠性。