直升機動力傳動鏈扭振抑制
匡傳樹,王 輝,江 希
(中國直升機設計研究所,江西 景德鎮 333001)
0 引言
直升機動力傳動鏈扭振問題是導致旋翼噪聲和槳轂載荷突變的重要原因[1-4],也會進一步影響直升機飛行品質[5],導致直升機機頭低頻晃動,嚴重降低駕駛員的操控和舒適性,在直升機型號研制中必須解決。
直升機飛行過程中,旋翼受到槳距操縱和不對稱氣流作用,出現揮舞、擺振運動,使其對動力傳動鏈的反扭矩發生周期性變化,引起動力傳動鏈轉速波動,反過來又對槳葉擺振產生影響,導致了旋翼集合型擺振與動力傳動鏈扭轉之間的耦合動力學問題。
現代直升機的渦輪軸發動機采用動力渦輪轉速(Np)閉環自動控制,以滿足直升機飛行控制的需求。扭矩負載變化引起動力傳動鏈轉速變化時,發動機控制系統則會按照設定的控制規律自動朝恢復Np目標轉速的方向調節油門[6]。根據自動控制原理,閉環控制系統一般存在控制穩定性問題。當發動機控制系統對扭振引起的Np波動的穩定性裕度偏低時,動力傳動鏈的扭振與發動機控制系統的功率調節會產生耦合控制問題。
針對直升機動力傳動鏈的扭振問題,國內外已有大量研究[7-11],工程上實施了有效的措施進行扭振抑制。在以往研究成果的基礎上,本文對直升機動力傳動鏈上的所有部件進行逐層分析,忽略次要因素,推導出簡單適用的固有特性計算方法;對渦軸發動機的氣動阻尼和轉速控制進行分析,建立動力傳動鏈負載與發動機控制系統組成的轉速控制模型,研究直升機動力傳動鏈扭振的抑制方法。
1 傳動系統動力學分析
直升機動力傳動鏈是動力渦輪、傳動鏈系、旋翼、尾槳和其它負載等組成的動力鏈路。整個鏈路的動力學較為復雜,需先開展對傳動系統、旋翼的單獨分析,再進行整體分析。
傳動系統由動力傳動鏈上的扭轉剛度極大的傳動部件如旋翼槳轂、尾槳、齒輪、傳動軸、動力渦輪等組成。從輸出端到輸入端,各傳動部件的轉動慣量分別為Ij,扭轉剛度和阻尼系數為分別kj和cj。
各傳動部件轉速統一表示為[12]:
Ωj=ij(Ω+Ωj,v)
(1)
其中,ij為傳動比,Ω為旋翼轉速(槳轂轉速),Ωj,v為相對轉速。
各傳動部件的動力學方程為:

(2)
其中φj、ψj分別為傳動部件的輸入、輸出彈性扭轉角。
相鄰部件扭矩傳遞的等式為:
ijkjφj=ij+1kj+1ψj+1
(3)
相鄰部件在接觸點具有相同的線速度,轉速與彈性扭轉角存在以下等式:

(4)
將式(1)代入式(4),則有:
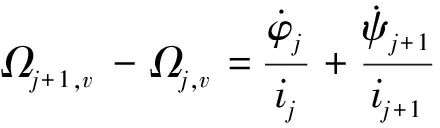
(5)
將等式(3)、(5)代入動力學方程(2),得到各轉動部件的動力學方程如下:
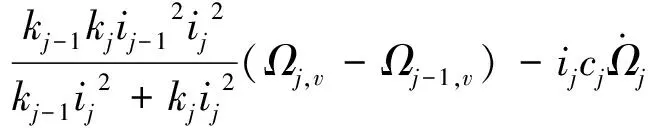
(6)
求解得到的Ωk,v為高頻小量,在與旋翼組成的低頻扭振系統中可以忽略。
上式對于含有多條支鏈的傳動鏈同樣可用。由于動力傳遞的對偶性,在傳動鏈分支處進行累加,在傳動鏈末端處前項或后項改為外部扭矩,得到:
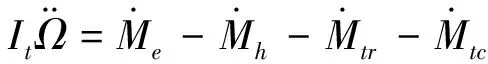
(7)
其中:
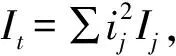
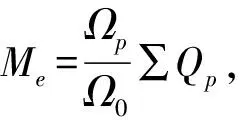
Mh=∑Mb,為旋翼槳轂受到的反扭矩總和;
Mtr為尾槳和其它負載總的等效反扭矩;
Mtc=∑cjΩj,為動力傳動鏈的阻尼力矩。
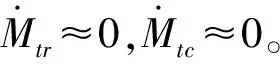
因此,直升機飛行過程中,傳動系統是一個內部扭轉剛度極大的系統,可以等效為剛體。其轉速波動主要受發動機輸出扭矩、旋翼槳轂反扭矩波動的影響。
2 旋翼動力學分析
根據式(7),旋翼與傳動鏈的扭振耦合表現為所有槳葉的反扭矩總和(Mh=∑Mb)與傳動鏈扭振之間的關聯作用,而槳葉的反扭矩與其擺振運動相關。
槳葉的擺振運動是其在旋轉平面內相對安裝位置的前后擺動(詳見圖1),擺振動力學方程為:
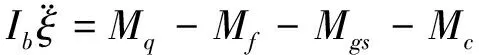
(8)
或者:
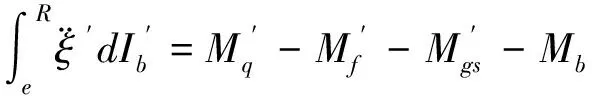
(9)
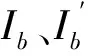

根據三角正弦定理:
則:
其中,Sb為槳葉相對軸承中心的質量靜矩。
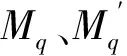

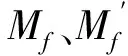
Mgs、Mgs′分別為槳葉揮舞運動引起的哥氏力相對軸承中心、槳轂中心的力矩:
Mc為槳葉額定轉速下的離心力在后擺狀態相對擺振軸承中心的力矩:

由式(8)得:
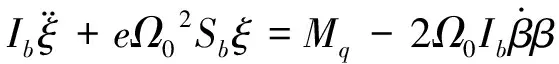
(10)
由式(9)得:

(11)
從而得到槳葉對槳轂的反扭矩:
Mb與槳葉的后擺角成正比,表明動力傳動鏈的扭振激勵來源于旋翼集合型擺振。根據直升機空氣動力學,槳葉氣動阻力矩交變部分可忽略,槳葉擺振的激勵來源主要為槳葉周期性的揮舞運動,槳葉揮舞運動的表達公式如下[13,14]:
β(t)=β0-β1cos(Ω0t)-β2sin(Ω0t)
其中,β為槳葉的揮舞角,β0、β1、β2為槳葉的揮舞系數;n為槳葉片數,G為直升機重量,m為單片槳葉的質量,φ7為總距角,θ1和θ2分別為橫向和縱向周期變距角,μ為前進比。
穩定飛行時所有槳葉的哥氏力矩之和為0,所以槳葉的揮舞運動不會引起持續的集合型強迫擺振;但在總距操縱時,各片槳葉的揮舞運動會出現相同相位的變化,激起旋翼集合型擺振。
3 完整的動力傳動鏈動力學特性
根據上述分析,動力傳動鏈扭振系統可以簡化為傳動系統剛體轉動和旋翼集合型擺振的兩自由度系統。式(10)、(11)未考慮槳轂轉速Ω與槳葉后擺角ξ的運動耦合,僅適用于激振分析。完整的動力傳動鏈動力學特性分析則需采用能量法。
1) 根據式(7)、(8),系統的動能為:
2) 根據槳葉離心力矩計算公式,系統的勢能為槳葉后擺產生的離心勢能:
應用拉格朗日方程得到直升機整個動力傳動鏈扭振無阻尼的齊次微分方程為:
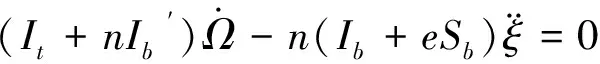
(12)
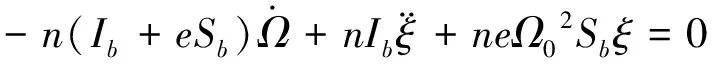
(13)
從而,系統的慣量矩陣和剛度矩陣分別為:
特征方程為:
Δ(ω2)=|K-ω2M|=0
計算得到系統的固有頻率為:
上述分析過程未考慮旋翼槳葉的擺振阻尼及動力渦輪的氣動阻尼,計算的扭振固有頻率高于直升機試驗測量的扭振頻率,約為3%。
渦輪軸發動機除了其控制系統的Np恒轉速閉環控制會響應動力傳動鏈轉速波動外,其動力渦輪本身也存在與Np轉速的氣動耦合作用,在Np小波動范圍內
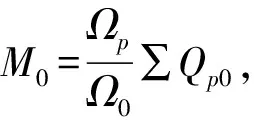

將Me代入式(12)右側,得到
(14)
表明發動機動力渦輪氣動耦合作用可以轉化為對動力傳動鏈扭振的阻尼。該阻尼與總功率成正比,隨前飛速度呈馬鞍形變化,在小重量中等飛行速度下對動力傳動鏈扭振的抑制作用最小。
4 發動機閉環控制穩定性
發動機控制系統采用雙閉環串聯控制回路,外環為Np控制回路,內環為Ng控制回路[16]。Np控制回路是目標參數控制回路,而Ng控制回路是提高控制效率的加強回路。
直升機動力傳動鏈負載與發動機控制系統組成的轉速控制原理圖如圖2所示。
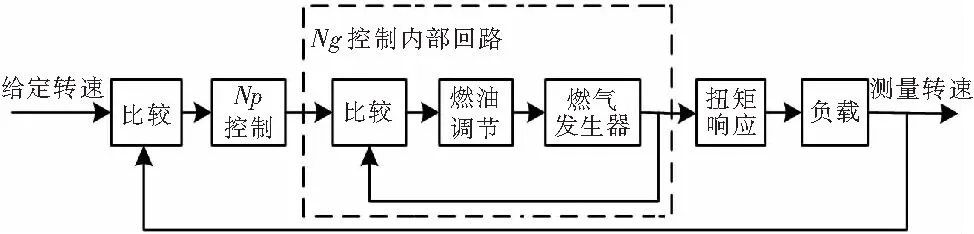
圖2 直升機旋翼轉速控制原理圖
對各個環節的傳遞函數分析如下:
1)負載環節
對方程(13)、(14)進行拉普拉斯變換后得到:
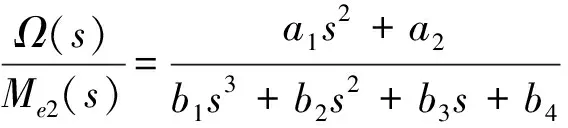
(15)
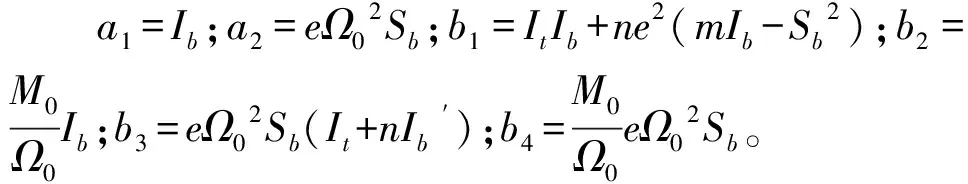
2)比較環節
E(s)=Ωdem(s)-Ω(s)
(16)
3)Np控制環節
動力渦輪轉速偏差到燃氣發生器轉速的傳遞函數等效于一個比例積分環節:
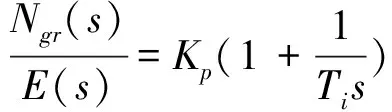
(17)
4)Ng控制回路
Ng控制回路簡化為一個含有比較環節、燃調響應環節、燃氣發生器響應環節的閉環回路。
燃調的計量活門對電調輸入信號的響應簡化為慣性傳遞函數。燃氣發生器的響應延遲時間一般達到100 ms以上,不能忽略[17],其響應簡化為慣性延遲傳遞函數。
從而Ng控制回路的傳遞函數為:
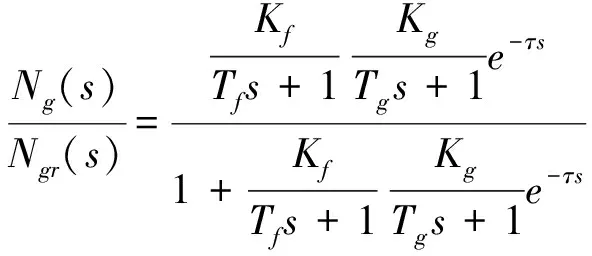
(18)
其中,τ為燃氣發生器延遲時間。
5) 扭矩響應環節
扭矩響應可簡化為一個一階微分環節:
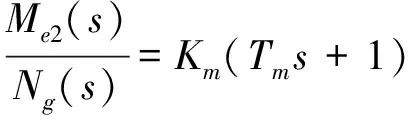
(19)
根據發動機對各個環節的設計參數,開展動力傳動鏈扭振的頻率特性和轉速波動響應特性分析,得到動力傳動鏈的轉速響應曲線如圖3所示,以及頻率特性如圖4所示,與直升機飛行數據相符。根據動力傳動鏈轉速閉環控制的特性分析,可以評估和修正轉速控制的穩定性[18]。
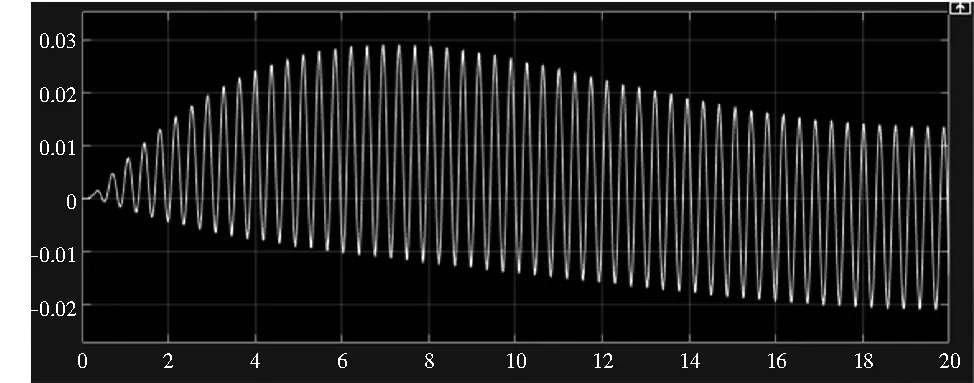
圖3 扭振固有頻率激勵下的轉速響應曲線
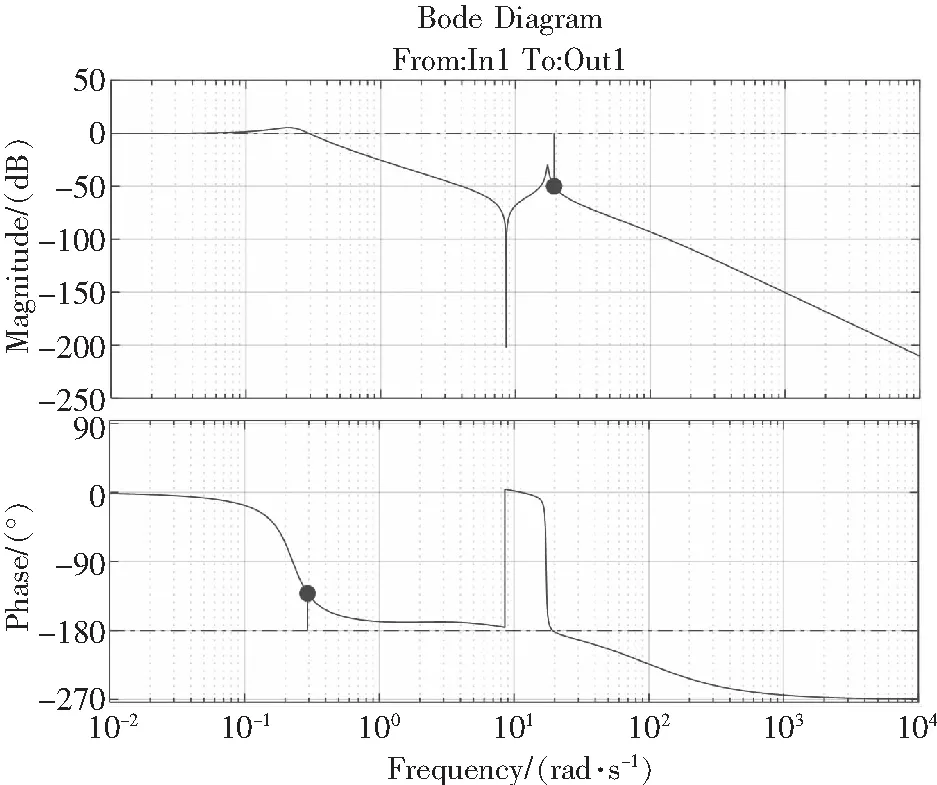
圖4 動力渦輪轉速控制回路BODE圖
直升機發動機控制系統增加轉速凹陷濾波器可以有效提高轉速控制的幅值裕度,但某些發動機控制系統的相位裕度偏低,穩定性仍然不能滿意,還需進一步解決。根據仿真和試驗數據分析,發動機燃氣發生器的響應延遲時間τ對系統的相位裕度有較大的影響。延遲時間τ主要與燃油系統的流阻、燃燒室工作特性有關,從而在工程設計中可適當改進燃油系統的尺寸設計,提高相位裕度,更好地抑制扭振。
5 結束語
本文通過對直升機動力傳動鏈扭振和旋翼揮舞、擺振的耦合動力學分析,以及對動力傳動鏈轉速閉環控制的穩定性分析,主要得到以下結論:
1)直升機動力傳動鏈的扭振激勵來源于旋翼集合型擺振,在較大的飛行重量和前飛速度條件下,進行槳距操縱或遭遇環境氣流時,槳葉的集合型擺振激勵較大,更容易激起動力傳動鏈的扭振;
2)直升機動力傳動鏈扭振系統可以簡化為傳動系統剛體轉動和旋翼集合型擺振的兩自由度系統,采用能量法可以求解較為準確的扭振固有頻率;
3)發動機動力渦輪氣動耦合作用可以轉化為對動力傳動鏈扭振的阻尼,該阻尼與總功率成正比,隨前飛速度呈馬鞍形變化,在小重量中等飛行速度下對動力傳動鏈的扭振抑制作用最小;
4)根據動力傳動鏈轉速閉環控制的特性分析,可以評估和修正發動機控制系統的穩定性,采用對應的措施進行扭振抑制。

