基于控制場的高精度相機(jī)標(biāo)定技術(shù)研究
陳 洋
(中國航空工業(yè)集團(tuán)公司洛陽電光設(shè)備研究所,河南 洛陽 471000)
0 引言
高精度測量技術(shù)是支撐經(jīng)濟(jì)高質(zhì)量發(fā)展的重要技術(shù)之一,經(jīng)常應(yīng)用在高端制造中,是一項不可或缺的重要組成部分[1]。隨著科技的進(jìn)步,我國的高端制造業(yè)正在高速發(fā)展,對精密測量技術(shù)的需求也日益迫切,同時對其技術(shù)要求也不斷提高,因此出現(xiàn)了很多新的測量需求和要求。但是傳統(tǒng)的測量方法在面對這些新的測量需求時,測量精度已經(jīng)無法有效滿足應(yīng)用需求,所以需要一種高精度的新測量方法來解決傳統(tǒng)測量面臨的問題[2],高精度視覺測量技術(shù)應(yīng)運而生。
視覺測量具有非接觸、實時測量、精度高以及可以自動化測量等優(yōu)點[3-4],在高端制造業(yè)以及工業(yè)等領(lǐng)域需要高精度實時非接觸測量等領(lǐng)域應(yīng)用廣泛。由于視覺測量的相機(jī)加工存在誤差,視覺測量的精度取決于測量相機(jī)參數(shù)的標(biāo)定精度,在進(jìn)行測量前,要對相機(jī)的參數(shù)進(jìn)行標(biāo)定,用來補償測量過程的誤差。對于空間中較小的物體,在采用視覺測量時,相機(jī)參數(shù)標(biāo)定往往采用高精度的平面靶標(biāo)對相機(jī)進(jìn)行參數(shù)標(biāo)定,就能夠滿足測量精度;但是在對空間中大型物體進(jìn)行測量時,由于測量及成像空間大,如果測量精度要求高,大尺寸的高精度平面靶標(biāo)加工難度大,精度無法保證,通常采用高精度的三維靶標(biāo)進(jìn)行相機(jī)參數(shù)標(biāo)定來保證測量精度。
本文針對大尺寸高精度測量提出了一種基于控制場的相機(jī)標(biāo)定方法,并通實驗證明標(biāo)定方法的正確性及精度,具有較高使用價值。
1 標(biāo)定方法及原理
1.1 相機(jī)成像模型
相機(jī)的成像模型可以用簡單的小孔成像模型來表示,小孔成像模型中用兩組參數(shù)來表示空間三維點和相機(jī)成像平面二維點之間的透視投影關(guān)系,一組參數(shù)是測量相機(jī)的內(nèi)參數(shù),一組是測量相機(jī)外參數(shù),假設(shè)相機(jī)成像符合理想的小孔成像模型,相機(jī)內(nèi)參數(shù)包括:實際焦距f、傳感器像元大小(dx,dy)和圖像的主點坐標(biāo)(u0,v0);對于實際的成像相機(jī)模型,由于存在加工和裝配等誤差,除了上述參數(shù)外,相機(jī)內(nèi)參數(shù)還應(yīng)包括:徑向畸變參數(shù)(k1,k2,k3)、切向畸變參數(shù)p1,p2;相機(jī)的外參數(shù)包括:3×3的正交旋轉(zhuǎn)矩陣R和3×1的平移矩陣T。
定義OwXwYwZw為外部物體的世界坐標(biāo)系,Ow為世界坐標(biāo)系原點,OcXcYcZc為相機(jī)坐標(biāo)系,Oc為光心,Ofuv為像素坐標(biāo)系,Oxy為像面坐標(biāo)系。小孔成像模型如圖1所示。
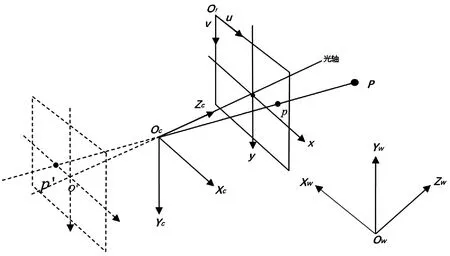
圖1 小孔成像模型
1.2 相機(jī)鏡頭畸變模型
設(shè)任意一點p的坐標(biāo)為(up,vp)和(xp,yp)知:
xp=(up-u0)dx
yp=(vp-v0)dy
(1)
相機(jī)鏡頭的畸變模型為[5]:
(2)
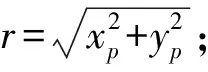
1.3 透視投影變換原理
設(shè)空間任意一點在空間世界坐標(biāo)系下的坐標(biāo)為(Xwp,Ywp,Zwp),齊次坐標(biāo)為(Xwp,Ywp,Zwp,1),p在相機(jī)坐標(biāo)系下的坐標(biāo)為(Xcp,Ycp,Zcp),點p在像面坐標(biāo)系下的齊次坐標(biāo)為(xp,yp,1),世界坐標(biāo)系到相機(jī)坐標(biāo)系的旋轉(zhuǎn)矩陣為R,平移矩陣為T。
由透視投影關(guān)系可以得p點世界坐標(biāo)系坐標(biāo)和投影點像面坐標(biāo)的關(guān)系:
(3)
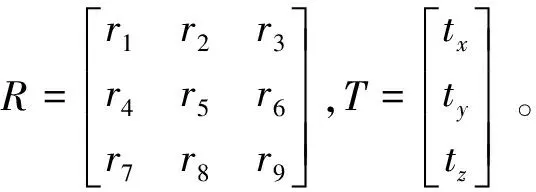
展開式(3)可以得到:
(4)
考慮相機(jī)成像畸變(4)式可寫為:
(5)
1.4 構(gòu)造相機(jī)參數(shù)求解模型
設(shè)空間中有n個點,在世界坐標(biāo)系下的坐標(biāo)為(Xwi,Ywi,Zwi),在相機(jī)像面坐標(biāo)系下的坐標(biāo)為(xi,yi),其中i=1,2,3,...,n。
由(5)式設(shè):
(6)
又由旋轉(zhuǎn)矩陣具有的正交性質(zhì),滿足6個正交約束方程:
(7)
由式(6)(7)可以構(gòu)造求解相機(jī)參數(shù)的無約束的最優(yōu)目標(biāo)函數(shù):
(8)
式(6)(7)(8)中:x=[fu0v0k1k2k3p1p2r1r2r3r4r5r6r7r8r9txtytz]為待求解相機(jī)參數(shù)矩陣。
1.5 相機(jī)參數(shù)L-M優(yōu)化求解流程
由最優(yōu)目標(biāo)函數(shù)F(x),令:
f(x)=[F11(x)...F1n(x)F21(x)...
F2n(x)H1(x)...H6(X)]r
(9)
令J(x)為f(x)的雅克比矩陣,知:
其中,i=1,2,3,...,n;j=1,2,...,6。
利用DLT求得F(x)初值x0,選取優(yōu)化初始參數(shù)α>0,增長因子β>1,迭代終止條件為δ>0,且δ是很小的實數(shù),I20×20為單位矩陣,設(shè)K=0。
利用L-M優(yōu)化算法求解相機(jī)參數(shù)的具體流程如下。
步1:置α=α/β。
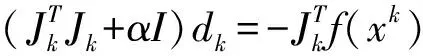
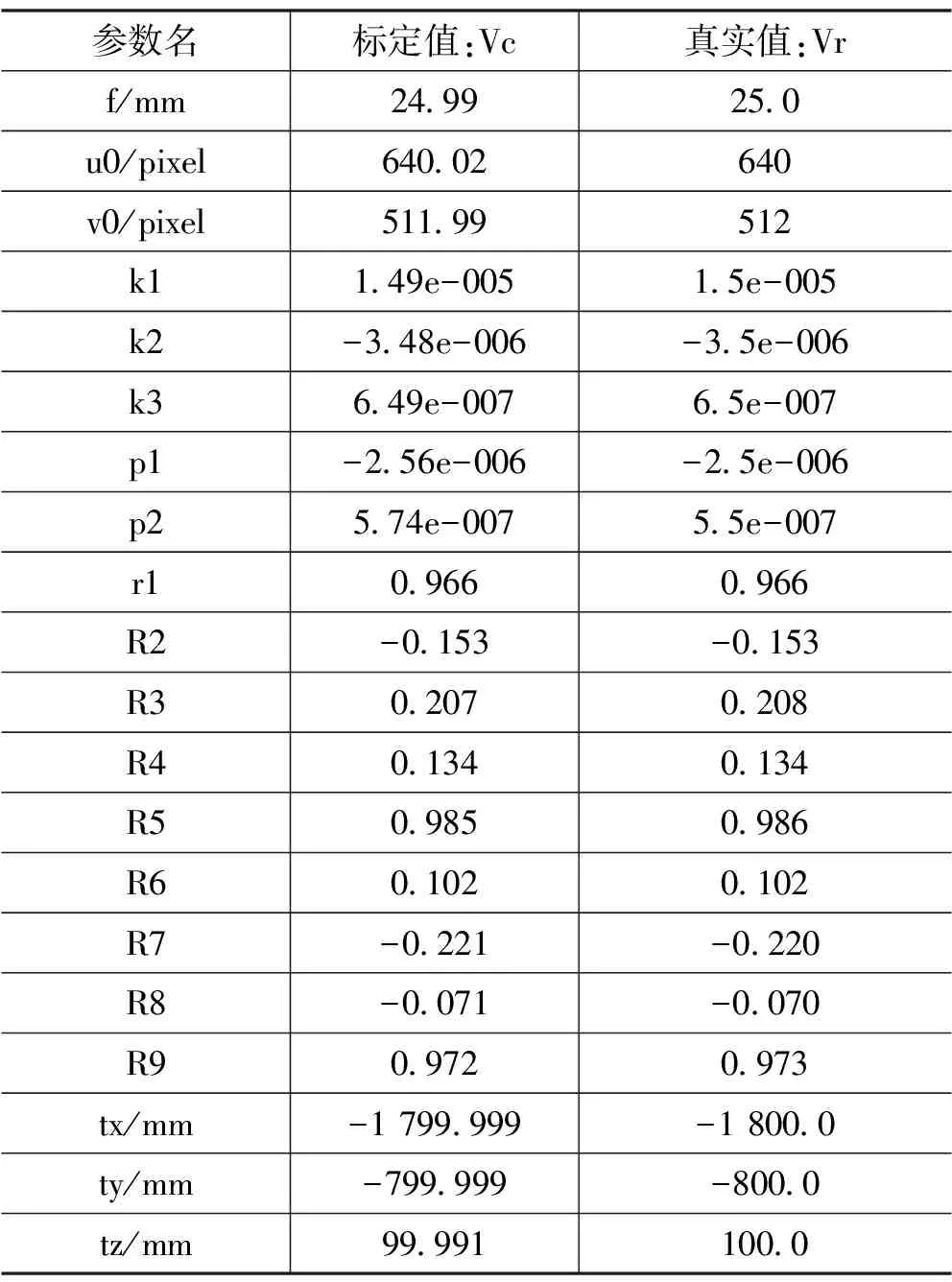
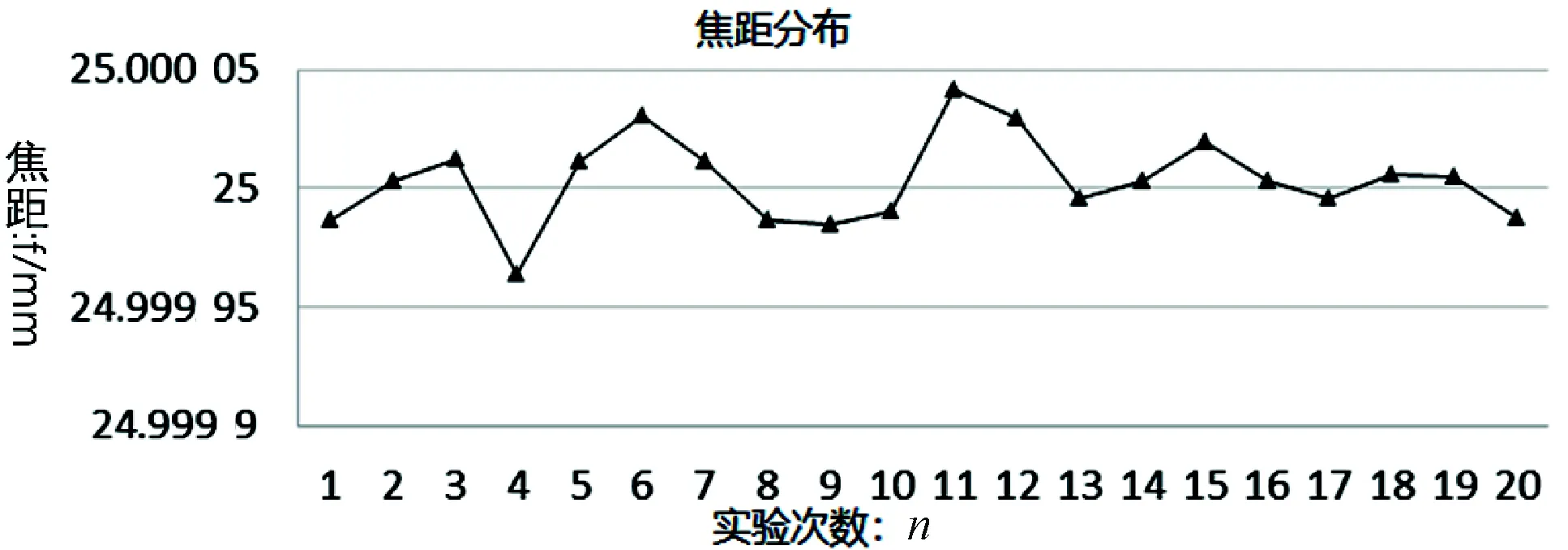
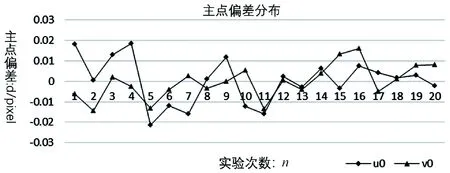
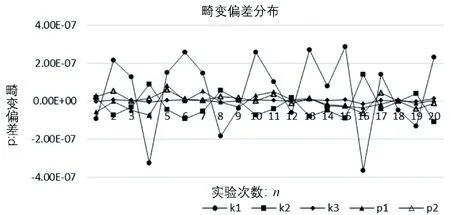
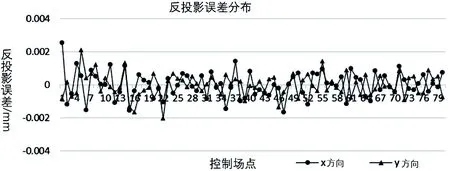
步3:若F(xk+1) 經(jīng)過有限次迭代計算,可求得到相機(jī)的內(nèi)外參數(shù)。 為了驗證相機(jī)標(biāo)定方法的正確性和高精度,構(gòu)造相機(jī)模型,內(nèi)參數(shù):焦距f=25 mm;傳感器x方向像元大小dx=5.3 μm,傳感器y方向的像元大小dy=5.3 μm;成像大小為1 280×1 024;主點選取理論值(u0,v0)=(640,512);徑向畸變:k1=1.5e-5,k2=-3.5e-6,k3=6.5e-7;切向畸變:p1=-2.5e-6,p2=5.5e-7;控制場坐標(biāo)系到相機(jī)坐標(biāo)系的旋轉(zhuǎn)矩陣R和平移矩陣T如下式: (10) 使用本文提出的標(biāo)定方法,可以計算出相機(jī)的內(nèi)外參數(shù)如表1所示。 表1 相機(jī)參數(shù)對比 模擬控制場標(biāo)定相機(jī)參數(shù)和相機(jī)參數(shù)真實值對比如表1所示。本算法標(biāo)定值偏離真實值極小,標(biāo)定值幾乎與真實值相等,是因為標(biāo)定過程中空間三維特征點坐標(biāo)和像素二維點坐標(biāo)都是根據(jù)相機(jī)成像模型仿真出的理想空間點,沒有成像誤差所致,實際應(yīng)用過程中,由于在測量三維點時存在定位誤差、控制場特征點成像時也存在二維點定位誤差,實際標(biāo)定結(jié)果和真實值的偏差一般會略大于理想情況下的偏差。 為了驗證標(biāo)定算法的穩(wěn)定性,通過指定的20組不同的世界坐標(biāo)系到相機(jī)坐標(biāo)系的旋轉(zhuǎn)平移矩陣,利用本論文標(biāo)定算法計算相機(jī)內(nèi)參,結(jié)果如圖2—4所示。 圖2 焦距 圖3 主點偏差 圖4 畸變偏差 由20次相機(jī)參數(shù)標(biāo)定實驗數(shù)據(jù)可知:20次試驗標(biāo)定的相機(jī)焦距平均值favg=25.000 003 51 mm,標(biāo)定的相機(jī)成像主點參數(shù)偏差絕對值的平均值uavg=0.008 76 pixel,vavg=0.006 374 pixel,畸變參數(shù)標(biāo)定結(jié)果偏差絕對值的平均值k1avg=1.756e-7,k2avg=5.743e-8,k3avg=5.737e-9,p2avg=2.33e-8,由20次試驗結(jié)果可知相機(jī)內(nèi)參標(biāo)定結(jié)果具有很高的穩(wěn)定型。 實際實驗中使用的是灰點公司的工業(yè)相機(jī),相機(jī)成像像素大小為1 280×1 024,相機(jī)傳感器像元大小dx=dy=5.3 μm,相機(jī)鏡頭焦距為f=25 mm。三維控制場由8根貼有反光標(biāo)志點的柱子組成,共有80個反光標(biāo)志點,標(biāo)志點的三維坐標(biāo)已提前通過工業(yè)數(shù)字近景攝影三維坐標(biāo)測量系統(tǒng)獲得。 通過相機(jī)對控制場特征點成像,獲取特征點在相機(jī)成像平面的二維像素坐標(biāo),利用本論文的標(biāo)定算法獲得相機(jī)內(nèi)外參數(shù)。 對于三維空間中任意一點p,設(shè)其空間三維坐標(biāo)為(Xwp,Ywp,Zwp),在相機(jī)坐標(biāo)系下的三維坐標(biāo)為(Xcp,Ycp,Zcp),像素坐標(biāo)(up,vp),像面坐標(biāo)為(xp,yp),世界坐標(biāo)系到相機(jī)坐標(biāo)系的旋轉(zhuǎn)矩陣為R,平移矩陣為T,則知: (11) 由小孔成像模型知p點像面坐標(biāo): (12) 由式(1)(2)(11)(12)知p點在x、y方向的反投影誤差表示為: (13) 假設(shè)空間中有n個點,則n個點在x、y方向的平均反投影誤差定義為: 利用標(biāo)定的相機(jī)參數(shù)計算控制場點反投影誤差如圖5所示。 圖5 反投影誤差分布 利用本論文提出的方法,利用控制場上80個特征點對相機(jī)進(jìn)行標(biāo)定,獲得相機(jī)參數(shù)對控制場上80個特征點在x和y方向的平均反投影誤差達(dá)到0.1個像素,具有較高的標(biāo)定精度,可以滿足空間大視場的高精度測量,具有較高的應(yīng)用價值。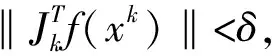
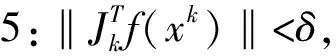
2 MATLAB仿真實驗
2.1 構(gòu)造相機(jī)模型及虛擬控制場
2.2 相機(jī)標(biāo)定及數(shù)據(jù)分析
2.3 相機(jī)內(nèi)參標(biāo)定穩(wěn)定性實驗
3 實際標(biāo)定實驗
3.1 相機(jī)參數(shù)標(biāo)定
4 結(jié)語

