基于NURBS和Slerp插補(bǔ)機(jī)器人S型速度規(guī)劃

龐智慧,王桂榮,陳 曉

(1. 中國(guó)計(jì)量大學(xué)機(jī)電工程學(xué)院,浙江 杭州 311018;2. 浙江錢(qián)塘機(jī)器人及智能裝備研究有限公司,浙江 杭州 310000)

1 引言

工業(yè)機(jī)器人的作業(yè)過(guò)程中,末端軌跡的柔順性是評(píng)價(jià)機(jī)器人作業(yè)質(zhì)量的重要指標(biāo)之一[1]。實(shí)際工業(yè)生產(chǎn)過(guò)程中,欲使機(jī)器人按照規(guī)劃路徑運(yùn)動(dòng),一般要經(jīng)過(guò)軌跡規(guī)劃、速度規(guī)劃、插補(bǔ)三個(gè)階段[2]。

機(jī)器人末端的軌跡規(guī)劃包含對(duì)末端位置和姿態(tài)的規(guī)劃。李永梅等[3]針對(duì)機(jī)器人的碼垛作業(yè),根據(jù)路徑點(diǎn)要求,設(shè)計(jì)了多段直線的末端軌跡,保證精確通過(guò)各路徑點(diǎn),適用于對(duì)作業(yè)精度要求不很精確的情形;John[4]以?huà)佄锞€過(guò)渡為例,運(yùn)用直線+多項(xiàng)式曲線過(guò)渡的方式,在復(fù)雜曲線的關(guān)鍵路徑點(diǎn)附近采用多項(xiàng)式曲線過(guò)渡,得到了較為光滑的末端軌跡,但此算法的復(fù)雜度隨著中間點(diǎn)的增多而急劇上升。而且,上述算法主要針對(duì)末端姿態(tài)不變的情形,如末端姿態(tài)發(fā)生變化,要根據(jù)描述末端姿態(tài)的方式,選用對(duì)應(yīng)的規(guī)劃方式[5]。李黎等[6]基于RPY角描述末端姿態(tài)的方式,對(duì)三個(gè)角度分別進(jìn)行規(guī)劃,結(jié)合對(duì)位置變量,實(shí)現(xiàn)了末端位姿軌跡的規(guī)劃。此方法適用于絕大多數(shù)姿態(tài),但T. Teramae[7]指出,當(dāng)繞任意軸旋轉(zhuǎn)角接近0°或180°時(shí)調(diào)整繞固定軸旋轉(zhuǎn)的相鄰姿態(tài)會(huì)出現(xiàn)姿態(tài)的過(guò)渡不連續(xù);Y. Nakamura[8]采用四元數(shù)描述旋轉(zhuǎn)運(yùn)動(dòng)可有效避免上述問(wèn)題,可以用來(lái)描述機(jī)器人末端的姿態(tài)。

上述對(duì)機(jī)器人末端進(jìn)行軌跡規(guī)劃時(shí),解決了末端按照何種路徑作業(yè)的問(wèn)題;而速度規(guī)劃解決了機(jī)器人經(jīng)過(guò)規(guī)劃路徑的方式。J. R[9]對(duì)比了梯形速度規(guī)劃和S型速度規(guī)劃,指出梯形速度曲線由0加速到勻速vmax的過(guò)程中,會(huì)出現(xiàn)加速度的突變,作業(yè)過(guò)程會(huì)出現(xiàn)抖動(dòng),而S型速度曲線將作業(yè)過(guò)程的速度分為加加速、勻加速、減加速、勻速、減減速、勻減速、加減速7段,保證了加速度的連續(xù)性,有效避免了速度突變,進(jìn)而改善作業(yè)質(zhì)量。

本文針對(duì)六軸串聯(lián)型機(jī)器人,對(duì)光滑性較好的NURBS曲線,運(yùn)用S型速度規(guī)劃方法,實(shí)現(xiàn)了末端軌跡的柔順性,及作業(yè)過(guò)程中關(guān)節(jié)空間與笛卡爾空間下速度的平滑,確保加速度不會(huì)發(fā)生突變,保證了機(jī)器人作業(yè)過(guò)程的平穩(wěn)性,減小機(jī)器人作業(yè)時(shí)的沖擊與抖動(dòng)。最后,通過(guò)仿真與實(shí)驗(yàn),對(duì)本文算法進(jìn)行驗(yàn)證。

2 機(jī)器人末端軌跡構(gòu)造

對(duì)于機(jī)器人末端作業(yè)路徑的規(guī)劃,一般先確定作業(yè)過(guò)程中的關(guān)鍵點(diǎn),通過(guò)插補(bǔ)構(gòu)造末端路徑。其中,以微小直線段連接相鄰關(guān)鍵路徑點(diǎn)的方式最為簡(jiǎn)單,但在兩相鄰線段的公共點(diǎn)處,會(huì)有方向的突變,整個(gè)作業(yè)過(guò)程也會(huì)有很多不光滑點(diǎn),從而影響作業(yè)的質(zhì)量。文獻(xiàn)[3]的規(guī)劃方法在構(gòu)造復(fù)雜軌跡時(shí)捉襟見(jiàn)肘,文獻(xiàn)[4]的規(guī)劃方法在中間點(diǎn)過(guò)多時(shí)算法效率較低,且缺少對(duì)末端姿態(tài)的規(guī)劃;而SHI[10]中提出的NURBS曲線可以根據(jù)一系列關(guān)鍵路徑點(diǎn)作為控制頂點(diǎn),并在不同的路徑點(diǎn)處給定不同的權(quán)因子,構(gòu)造出一種統(tǒng)一的曲線模型,同時(shí),由于NURBS曲線具有可微性,滿(mǎn)足機(jī)器人作業(yè)中對(duì)于末端軌跡的光滑性要求。此外,結(jié)合基于四元數(shù)描述的機(jī)器人末端姿態(tài)規(guī)劃,可以滿(mǎn)足復(fù)雜作業(yè)軌跡的要求。

2.1 NURBS曲線構(gòu)造

一般而言,一條k次NURBS曲線表達(dá)式如下式(1)

(1)

其中,di—n+1個(gè)控制頂點(diǎn),i=0,1,…,n;ωi—n+1個(gè)控制頂點(diǎn)處的權(quán)因子,ω0>0,ωn>0,其它ωi≥0;u∈[0,1]—?dú)w一化因子;U=[u0,u1,…,un+k+1]—節(jié)點(diǎn)向量,各ui非遞減;兩端節(jié)點(diǎn)處重復(fù)度一般取為k+1,u0=u1=…=uk=0,un+1=un+2=…=un+k+1=1;中間各ui步長(zhǎng)為1/(n+1-k),即uk+1=1/(n+1-k),uk+2=2/(n+1-k),…un=(n-k)/(n+1-k);Ni,k(u)—n+1個(gè)控制頂點(diǎn)處對(duì)應(yīng)的k次B樣條基函數(shù),詳見(jiàn)文獻(xiàn)[10]。由式(1)可知,NURBS曲線可以表示為笛卡爾空間下各坐標(biāo)分量的形式。

由文獻(xiàn)[11]中所述,NURBS曲線的一階、二階導(dǎo)數(shù)公式如下

(2)

(3)

其中p(u)=A(u)/w(u);根據(jù)式(1)中NURBS曲線的分量形式,結(jié)合式(2)、式(3)中NURBS曲線的一階、二階導(dǎo)數(shù)公式,可求得各節(jié)點(diǎn)處三個(gè)分量方向的速度、加速度。

運(yùn)用NURBS曲線進(jìn)行插補(bǔ)[12]時(shí),需要已知當(dāng)前時(shí)刻的弧長(zhǎng)才可進(jìn)行速度規(guī)劃。從p(u1)點(diǎn)到p(u2)點(diǎn)的NURBS曲線長(zhǎng)度L為

(4)

一般而言,式(4)中的被積函數(shù)很難得到原函數(shù),故選用文獻(xiàn)[13]所述的Simpson數(shù)值積分的方法計(jì)算NURBS曲線長(zhǎng)度,如下式(5)所示

(5)

2.2 基于四元數(shù)描述的機(jī)器人末端姿態(tài)規(guī)劃

由本文引言部分所述,基于四元數(shù)的機(jī)器人末端軌跡規(guī)劃可以插值得到平滑的旋轉(zhuǎn),有效解決RPY角線性插值時(shí)三維旋轉(zhuǎn)的不平滑問(wèn)題。

單位四元數(shù)有兩種描述形式

q=s+ai+bj+ck

(6)

(7)

式(7)中旋轉(zhuǎn)軸為f=fxi+fyj+fzk;

聯(lián)立式(6)、式(7),有

(8)

式(6)中所述四元數(shù)對(duì)應(yīng)的姿態(tài)矩陣為

(9)

笛卡爾空間下繞單位向量f旋轉(zhuǎn)θ角度,得到式(10)所述的旋轉(zhuǎn)矩陣

(10)

其中,逆時(shí)針旋轉(zhuǎn)為正,順時(shí)針為負(fù)。顯然,式(9)與式(10)等價(jià)。

聯(lián)立式(9)、式(10),有

(11)

由式(11)可直接由機(jī)器人末端姿態(tài)矩陣求出對(duì)應(yīng)的四元數(shù)。由于未規(guī)定旋轉(zhuǎn)方向,故對(duì)應(yīng)2個(gè)共軛的四元數(shù)。

對(duì)于由四元數(shù)描述的任意兩組姿態(tài)q0和q1,一般有兩種方法,Lerp和Slerp。Lerp即為線性插值,即

Lerp(q0,q1,h)=q0(1-h)+q1h

(12)

其中h可理解為NURBS曲線中的參數(shù)u,h∈[0,1]。

圖1中,Lerp插值沿著單位圓圓弧上從q0到q1的弦上插值,因此Lerp插值出來(lái)的四元數(shù)不是單位四元數(shù)。將插值得到的四元數(shù)正規(guī)化,為Nlerp插值,即

圖1 Lerp插值&Slerp插值

(13)

上述插值方法中,當(dāng)h在區(qū)間[0,1]內(nèi)均勻分布時(shí),得到的插補(bǔ)段并不是均勻分布的,即Lerp插值只具有形式上的“線性插值”。

Slerp(球面線性插值)是對(duì)角度的線性插值,即

θh=(1-h)θ0+hθ1

(14)

其中,θ0和θ1分別為四元數(shù)q0和q1的旋轉(zhuǎn)角。令θ0=0,則θh=hθ1。由文獻(xiàn)[7]可知,Slerp插值可以表述為

qh=Slerp(q0,q1,h)=αq0+βq1

(15)

(16)

Slerp插值給出了四元數(shù)描述的球面上兩點(diǎn)之間最短的插值曲線,且轉(zhuǎn)角均勻變化。為了提高四元數(shù)對(duì)姿態(tài)的規(guī)劃效率,避免姿態(tài)的冗余變化,選擇q1與-q1中與q0夾角較小的做Slerp插值,即

Slerp(q0,q1,h)=

(17)

Slerp插值對(duì)h一階、二階導(dǎo)數(shù)分別為

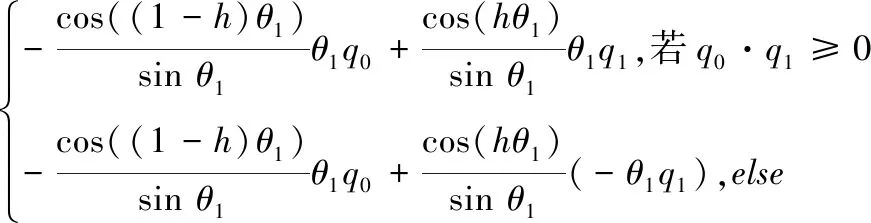
(18)

(19)

(20)

3 機(jī)器人軌跡規(guī)劃算法設(shè)計(jì)

本文設(shè)計(jì)的機(jī)器人軌跡規(guī)劃算法如下:

1)構(gòu)造末端軌跡

機(jī)器人的末端軌跡包含機(jī)器人末端的位置和姿態(tài),合稱(chēng)為位姿,是作業(yè)過(guò)程時(shí)間t的函數(shù);因此,可以對(duì)位置和姿態(tài)分別規(guī)劃。由本文第一章所述,機(jī)器人末端位置采用NURBS曲線規(guī)劃,姿態(tài)采用四元數(shù)的Slerp規(guī)劃;

2)劃分關(guān)鍵點(diǎn)

對(duì)Step1中構(gòu)造出的機(jī)器人末端軌跡按照機(jī)器人的插補(bǔ)周期劃分為n段,得到n+1個(gè)關(guān)鍵路徑點(diǎn);

3)對(duì)關(guān)鍵點(diǎn)處求逆解,逆解取優(yōu)

工業(yè)機(jī)器人的工作空間分為關(guān)節(jié)空間和笛卡爾空間。關(guān)節(jié)空間下機(jī)器人通過(guò)運(yùn)動(dòng)學(xué)正解可得到一組關(guān)節(jié)角對(duì)應(yīng)的末端位姿;反過(guò)來(lái),笛卡爾空間下通過(guò)機(jī)器人的運(yùn)動(dòng)學(xué)逆解可求得對(duì)應(yīng)的關(guān)節(jié)角,而且運(yùn)動(dòng)學(xué)逆解所得的關(guān)節(jié)角通常不唯一,需要進(jìn)行逆解取優(yōu)。

機(jī)器人正運(yùn)動(dòng)學(xué)方程為

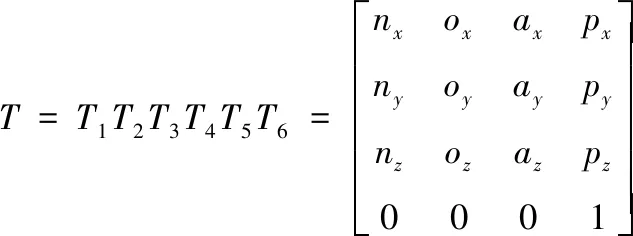
(21)

式(21)也可表述為

x=x(θ)

(22)

式(22)兩端對(duì)時(shí)間t求導(dǎo),有

(23)

式(23)也可表述為

(24)

式(24)兩端對(duì)時(shí)間t求導(dǎo),有

(25)

機(jī)器人的逆運(yùn)動(dòng)學(xué)求解,可以用KDL、IKFAST[15]等運(yùn)動(dòng)算法庫(kù)。KDL采用Newton-Raphson迭代法[16]求解運(yùn)動(dòng)學(xué)逆解的數(shù)值解;IKFAST針對(duì)滿(mǎn)足Pieper法則[17]的機(jī)器人,求解運(yùn)動(dòng)學(xué)逆解的解析解。機(jī)器人運(yùn)動(dòng)學(xué)逆解的求解速度直接影響了機(jī)器人軌跡規(guī)劃的實(shí)時(shí)性,因此選用一種快速準(zhǔn)確的運(yùn)動(dòng)算法庫(kù)具有重要的意義。

機(jī)器人求解運(yùn)動(dòng)學(xué)逆解時(shí),一般需要進(jìn)行逆解取優(yōu)。逆解取優(yōu)原則通常為各關(guān)節(jié)的運(yùn)動(dòng)變化量最小,即運(yùn)動(dòng)姿態(tài)變化最平緩。此處可以參照笛卡爾空間下位移的定義,定義關(guān)節(jié)空間下的“位移”

(26)

即式(26)中的Δθ最小,或Δθi最小。

4)在關(guān)節(jié)空間進(jìn)行S型速度規(guī)劃

S型速度規(guī)劃可以保證加速度連續(xù)變化,有效減小了機(jī)器人作業(yè)過(guò)程中關(guān)節(jié)電機(jī)的沖擊,避免作業(yè)過(guò)程中的頻繁起停,因此可選用S型速度曲線在關(guān)節(jié)空間下對(duì)各關(guān)節(jié)角度進(jìn)行規(guī)劃。

七段式S型速度規(guī)劃中,包含加加速、勻加速、減加速、勻速、減減速、勻減速、加減速7段加減速過(guò)程,如圖2所示:

圖2 七段式S型速度規(guī)劃

圖2中,每段結(jié)束時(shí)刻記為t1～t7,每段用時(shí)為T(mén)1～T7,位移為s,有

T1=T3=T5=T7,T2=T6

(27)

S型速度規(guī)劃中,五段式缺少勻加速、勻減速段,即T2=T6=0;六段式缺少勻速段,即T4=0;四段式缺少勻加速、勻速、勻減速段,即T2=T4=T6=0。

S型速度規(guī)劃流程圖如圖3所示。

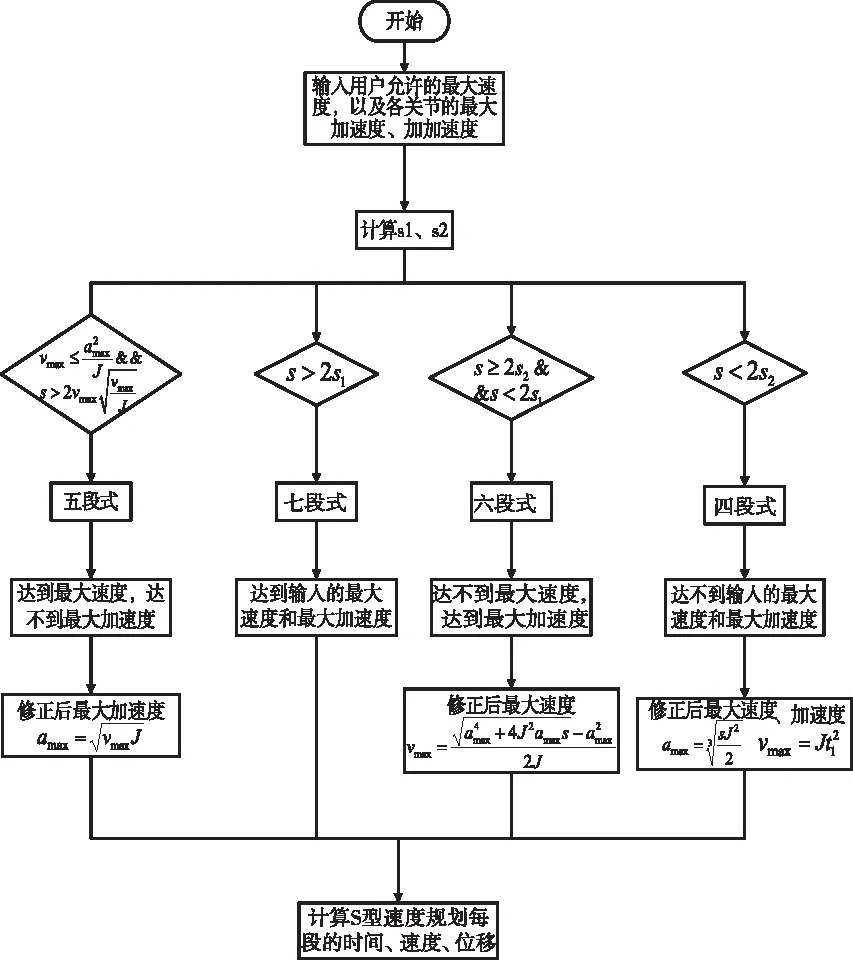
圖3 S型速度規(guī)劃流程

圖3中,s1、s2分別為經(jīng)過(guò)加加速段、勻加速段、減加速段達(dá)到最大速度完成的位移,以及僅經(jīng)過(guò)加加速段、減加速段達(dá)到最大速度完成的位移。

(28)

(29)

S型速度規(guī)劃過(guò)程中,需要輸入待規(guī)劃段的起點(diǎn)終點(diǎn)的位姿坐標(biāo)、輸入最大速度vmax、最大加速度amax,以及各關(guān)節(jié)電機(jī)的加加速度J,計(jì)算s、s1、s2,根據(jù)圖3中的規(guī)劃流程,判斷S型速度規(guī)劃的類(lèi)型,根據(jù)文獻(xiàn)[14]計(jì)算S型速度規(guī)劃過(guò)程中由本章(2)中n+1個(gè)關(guān)鍵路徑點(diǎn)所得n段軌跡的時(shí)間、速度、位移;之后按照機(jī)器人插補(bǔ)周期得到n段軌跡內(nèi)所有插補(bǔ)點(diǎn)的關(guān)節(jié)角,發(fā)送至各關(guān)節(jié)電機(jī),按照本文所述的規(guī)劃方式得出規(guī)劃軌跡,與原有激勵(lì)軌跡進(jìn)行對(duì)比分析;

5)將4)中n段軌跡內(nèi)規(guī)劃所得所有插補(bǔ)點(diǎn)的關(guān)節(jié)角度、角速度、角加速度代入式(22)、式(23)、式(25)所述運(yùn)動(dòng)學(xué)正解、速度、加速度的表達(dá)式,得到笛卡爾空間下位姿的各個(gè)分量關(guān)于時(shí)間t的曲線,以及末端速度、加速度曲線。

機(jī)器人末端軌跡規(guī)劃的流程圖如圖4所示。

圖4 機(jī)器人末端軌跡規(guī)劃流程圖

4 仿真結(jié)果分析

4.1 機(jī)器人運(yùn)動(dòng)學(xué)模型

機(jī)器人正逆運(yùn)動(dòng)學(xué)的求解,需要先建立機(jī)器人的連桿坐標(biāo)系,求解機(jī)器人的DH參數(shù)。本文采用SR4C機(jī)器人作為研究對(duì)象,其DH參數(shù)如表1所示:

表1 SR4C的DH參數(shù)

表1所示的DH參數(shù)表中,ai(mm)為連桿長(zhǎng)度,αi為扭轉(zhuǎn)角,di(mm)為連桿偏移量,θi為關(guān)節(jié)角。SR4C機(jī)器人各關(guān)節(jié)均為旋轉(zhuǎn)關(guān)節(jié),因此關(guān)節(jié)角可在限位范圍內(nèi)任意給定。

4.2 仿真結(jié)果分析

為了驗(yàn)證本文所述算法的有效性,選取機(jī)器人常用的伯努利雙紐線作為激勵(lì)軌跡,據(jù)此構(gòu)造NURBS曲線。伯努利雙紐線方程

(x2+y2)2=2a2(x2-y2)

(30)

(31)

取焦距a=50√2mm;激勵(lì)軌跡如圖5所示。

圖5 激勵(lì)軌跡

NURBS曲線參數(shù):曲線次數(shù)k=3;節(jié)點(diǎn)向量U=[0,0,0,0,1/313,2/313,…,312/313,1,1,1,1];控制頂點(diǎn)由式(32)確定:

(32)

其中i=0,1,…,315;式(32)為伯努利雙紐線的參數(shù)方程,其中θ取值范圍[0,π/4],[3π/4,5π/4],[7π/4,2π],θi步長(zhǎng)為0.01rad;控制因子為ω=[1,1,…,1];控制頂點(diǎn)個(gè)數(shù)n+1=316;所構(gòu)造NURBS曲線是機(jī)器人末端按照伯努利雙紐線作業(yè)時(shí),在機(jī)器人基坐標(biāo)系的坐標(biāo)表示。

機(jī)器人末端姿態(tài)的規(guī)劃采用本文2節(jié)所述的Slerp規(guī)劃,即轉(zhuǎn)角均勻變化。由式(21)中的機(jī)器人運(yùn)動(dòng)學(xué)方程可求出式(32)對(duì)應(yīng)的位姿矩陣,結(jié)合式(11)即可求得對(duì)應(yīng)的四元數(shù)。

本文中,由式(32)可以得到規(guī)劃過(guò)程中的所有路徑點(diǎn),結(jié)合本文算法可構(gòu)造出末端的激勵(lì)軌跡,輸入的速度、加速度、加加速度參數(shù)如表2所示:

表2 各關(guān)節(jié)參數(shù)

為了說(shuō)明本文所提算法的有效性,選取基于5次多項(xiàng)式的S型速度規(guī)劃的方式做對(duì)比,即式(32)中相鄰路徑點(diǎn)之間采用5次多項(xiàng)式構(gòu)造激勵(lì)軌跡,得到激勵(lì)軌跡的對(duì)比圖,如圖6所示。

圖6 本文算法與5次多項(xiàng)式

由圖6可知,相比于5次多項(xiàng)式的規(guī)劃方式,本文所提算法規(guī)劃出的軌跡更加接近真實(shí)的激勵(lì)軌跡,且軌跡的光滑性有顯著的提升。采用本文算法與5次多項(xiàng)式規(guī)劃的激勵(lì)軌跡的曲率圖如圖7所示。

圖7 不同規(guī)劃算法的曲率圖

其中,NURBS曲線上任意點(diǎn)曲率計(jì)算公式可由文獻(xiàn)[11]確定。

(33)

由圖7可知,采用5次多項(xiàng)式規(guī)劃所得的激勵(lì)軌跡只在有限個(gè)點(diǎn)處曲率值不為0,說(shuō)明5次多項(xiàng)式規(guī)劃的激勵(lì)軌跡由多段直線組成,激勵(lì)軌跡平滑性有待提高;而本文所提算法基于NURBS的曲線構(gòu)造方法,整段激勵(lì)軌跡上曲率均不為0,且曲率值低于原激勵(lì)軌跡,即構(gòu)造較為平緩的NURBS曲線,有效提高了激勵(lì)軌跡的平滑性。

根據(jù)圖4中的軌跡規(guī)劃流程,可得本文算法規(guī)劃所得的各關(guān)節(jié)位移、速度、加速度曲線,如圖8所示。

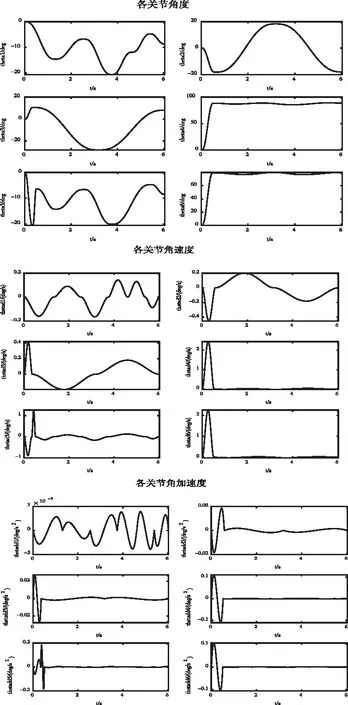
圖8 本文規(guī)劃下關(guān)節(jié)空間曲線

圖8中,按照本文所提規(guī)劃算法作業(yè)過(guò)程中,各關(guān)節(jié)的角加速度隨時(shí)間連續(xù)變化,未出現(xiàn)突變現(xiàn)象,保證了角速度、角度曲線的光滑性,避免了5次多項(xiàng)式規(guī)劃中出現(xiàn)的頻繁起停的問(wèn)題,減小了關(guān)節(jié)電機(jī)作業(yè)過(guò)程中的沖擊,一定程度上延長(zhǎng)了關(guān)節(jié)電機(jī)壽命;同時(shí),隨著關(guān)節(jié)電機(jī)角度曲線光滑性的提升,作業(yè)質(zhì)量也隨之改善。

5 小結(jié)

本文對(duì)工業(yè)機(jī)器人作業(yè)過(guò)程中末端軌跡的平滑性進(jìn)行研究,基于NURBS曲線規(guī)劃的方式構(gòu)造一出種統(tǒng)一的曲線模型,改善了作業(yè)路徑的平滑性;通過(guò)基于四元數(shù)的Slerp規(guī)劃方法對(duì)末端姿態(tài)使機(jī)器人末端姿態(tài)均勻變化,減少了姿態(tài)冗余的情形;S型速度曲線使得速度曲線變得平滑,避免了5次多項(xiàng)式規(guī)劃方式中機(jī)器人頻繁起停的問(wèn)題,各關(guān)節(jié)加速度不會(huì)產(chǎn)生突變,減小了作業(yè)過(guò)程中對(duì)關(guān)節(jié)電機(jī)的沖擊,保證了作業(yè)質(zhì)量,延長(zhǎng)了各關(guān)節(jié)電機(jī)的使用壽命。