基于自適應(yīng)魯棒的機械臂軌跡跟蹤控制

趙化民,呂成興,陳 健

(青島理工大學(xué)信息與控制工程學(xué)院,山東 青島 266520)

1 引言

近年來,隨著機器人技術(shù)的發(fā)展,如何在不增加成本的前提下提高機器人性能以達到更高的精度和速度受到越來越多的關(guān)注[1]。現(xiàn)階段的實際應(yīng)用中,在保證機械臂任務(wù)完成質(zhì)量與速度的同時,對于給定的軌跡達到期望的跟蹤精度成為了研究的熱點問題。

在機械臂軌跡跟蹤問題受到越來越多人關(guān)注的同時,針對軌跡跟蹤問題,各種優(yōu)良的控制策略被廣泛提出用以保證機械臂進行精確軌跡跟蹤。比如魯棒控制,自適應(yīng)控制以及滑模控制[2]等。自適應(yīng)控制可以在不確定因素和模型參數(shù)變化的情況下確保良好的系統(tǒng)性能,但這種方法需要大量計算設(shè)計控制律。傳統(tǒng)滑模控制[3,4]雖然有著較好的魯棒性和快速的響應(yīng)能力,但其會引起控制的抖振從而削減系統(tǒng)控制性能。文獻[5]提出的自適應(yīng)反步滑模控制,通過推導(dǎo)出精確的包含摩擦的機械臂動力學(xué)模型,使系統(tǒng)在存在外界干擾時仍可以進行精確的軌跡跟蹤。擾動觀測器[6-8]通常被用來處理系統(tǒng)所受干擾以及系統(tǒng)本身存在的一些不確定性,其因設(shè)計結(jié)構(gòu)簡單直觀而受到廣泛歡迎。文獻[9,10]為更好抑制抖振現(xiàn)象設(shè)計了一種基于擾動觀測器的非線性滑模控制器,同時提高了機械臂抗干擾能力。文獻[11]為解決系統(tǒng)的時滯效應(yīng)提出了一種帶有干擾觀測器與狀態(tài)觀測器的徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)(RBFNN)控制方案。Tran等[12]提出一種使用終端滑模控制(TSMC)和RBFNN的機械臂自適應(yīng)控制,此方法加快了系統(tǒng)響應(yīng)速度但TSMC仍存在奇異問題。魯棒自適應(yīng)[13]跟蹤控制方法也能夠很好的解決系統(tǒng)跟蹤問題且提高系統(tǒng)跟蹤精度。以上傳統(tǒng)算法雖然一定程度上提高了系統(tǒng)性能但未能使誤差在有限時間內(nèi)收斂或存在奇異問題。

文獻[14]采用一種遞歸分散有限時間控制,使跟蹤誤差在有限時間內(nèi)收斂到原點附近從而保證系統(tǒng)良好的跟蹤性能,但其方法較為復(fù)雜。Sun等[15]將隨機控制理論與自適應(yīng)技術(shù)結(jié)合設(shè)計了一種克服過度參數(shù)化問題的控制器,能夠保證跟蹤誤差的均方根任意小。文獻[16]通過一種新穎的雅可比矩陣自適應(yīng)(JMA)方法對機械臂進行跟蹤控制,同樣達到了期望跟蹤精度。文獻[17]以時延控制(TDC)為控制框架,提出一種無模型軌跡跟蹤控制方法,能夠保證較好的跟蹤精度,但其具有較大的計算量。在文獻[18]中,通過使用神經(jīng)網(wǎng)絡(luò)整定傳統(tǒng)PID的方法對機械臂進行控制,保證在最小的穩(wěn)態(tài)誤差下完成軌跡跟蹤。反步控制[19,20]設(shè)計過程獨特且具有較好的不確定性處理能力,但存在干擾時也會降低控制性能。以上雖不同于一些傳統(tǒng)方案,可以保證誤差在有限時間收斂,但未考慮摩擦等外部擾動對系統(tǒng)的影響。因此通過以上分析以及機械臂控制系統(tǒng)自身特點,針對機械臂受到復(fù)雜時變擾動時的高精度軌跡跟蹤問題,本文提出了一種帶擾動觀測器的機械臂自適應(yīng)魯棒軌跡跟蹤控制策略,能夠有效減小擾動對軌跡跟蹤的影響且使跟蹤誤差能夠在有限時間內(nèi)收斂。

本文主要創(chuàng)新工作如下:1)考慮帶有摩擦的機械臂動力學(xué)模型,反步跟蹤控制器有效地提高了軌跡跟蹤精度,并引入一階濾波器解決虛擬控制輸入的復(fù)雜求導(dǎo)問題。2)設(shè)計一種自適應(yīng)律更新擾動觀測器增益,提高了觀測器性能進而準確獲得擾動估計。3)所設(shè)計控制器控制精度與跟蹤速度均優(yōu)于非線性PD控制器。

2 機械臂動力學(xué)模型

考慮機械臂各關(guān)節(jié)類型為旋轉(zhuǎn)型,故串聯(lián)機械臂動力學(xué)模型推導(dǎo)化簡得到如下形式

(1)

其中M(q)∈n×n為機械臂慣性矩陣且為正定矩陣,n×n表示離心力與哥氏力矩陣,G(q)∈n代表重力項。n分別為關(guān)節(jié)角位移,角速度,角加速度向量。τ∈n為系統(tǒng)輸入向量,τd∈n為擾動向量,包括摩擦以及外部隨機干擾。本文采用摩擦項如下

(2)

其中φ1,φ2,φ3,γ1,γ2,γ3為設(shè)計參數(shù)。

該機械臂滿足以下動力學(xué)特性:

1)慣性陣M(q)為對稱正定且可逆矩陣,并存在正數(shù)Mmax,Mmin使其范數(shù)有界

(3)

(4)

由于存在外部干擾信號,為了能更好地跟蹤給定位置信號xd,做以下兩點假設(shè):

1)期望角度xd及其n階導(dǎo)數(shù)存在且有界。

3 控制系統(tǒng)設(shè)計

3.1 控制器設(shè)計

在機械臂控制中,由于模型不確定性以及系統(tǒng)所受外部干擾的影響,系統(tǒng)輸出不穩(wěn)定導(dǎo)致軌跡跟蹤效果差。反步法對不確定性有較好的處理能力,因此本文通過反步法設(shè)計系統(tǒng)的控制律,有效地提高了系統(tǒng)的跟蹤精度。通過擾動觀測器觀測系統(tǒng)所受干擾,得到估計值,較好地克服了擾動造成的對系統(tǒng)跟蹤性能的影響。系統(tǒng)結(jié)構(gòu)框圖如圖1。

圖1 系統(tǒng)結(jié)構(gòu)框圖

重新定義系統(tǒng)狀態(tài)變量如下

(5)

Step1)定義誤差向量e1=x1-xd,其中xd為期望軌跡,設(shè)計李雅普諾夫函數(shù)

(6)

定義虛擬控制量

(7)

其中k1為參數(shù)向量,引用以下一階濾波器:

(8)

最終V1對時間導(dǎo)數(shù)為

(9)

Step2:定義誤差向量e2=x2-α,設(shè)計李雅普諾夫函數(shù)

(10)

由誤差向量可知

(11)

忽略擾動時,由式(1),(9),(11)對(10)求導(dǎo)

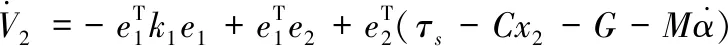
(12)

故取控制律τs為

(13)

3.2 擾動觀測器設(shè)計

一般情況下,通過估計的方法來獲取復(fù)合干擾τd。但估計值往往與實際值存在誤差,而擾動觀測器得原理就是對估計值進行修正。為了估計機械臂的擾動,很多作者提出了不同的觀測器設(shè)計方法,常用形式為非線性擾動觀測器。本文采用如下形式觀測器

(14)

器增益。

定義李亞普諾夫函數(shù)

(15)

由式(1)與(14)可知

(16)

對估計誤差求導(dǎo),并由式(16)得

(17)

因此,式(15)對時間的導(dǎo)數(shù)為

(18)

其中

(19)

ξ為正常數(shù),根據(jù)式(19),將(18)改寫為

≤-βV3+c

(20)

其中

β=2(P0-ξ),

(21)

(22)

3.3 自適應(yīng)律設(shè)計

為增強觀測器對擾動的觀測性能并簡化參數(shù)選取過程,通過式(13)設(shè)計自適應(yīng)律更新觀測器增益。首先構(gòu)造李雅普諾夫函數(shù)

(23)

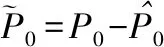
(24)

將式(13)代入

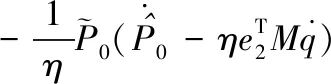
(25)

故取P0自適應(yīng)律為

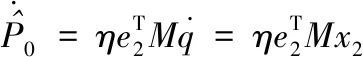
(26)

4 穩(wěn)定性分析

對整個系統(tǒng)構(gòu)造李雅普諾夫函數(shù)

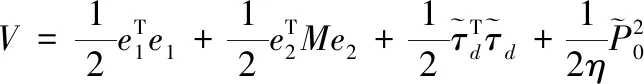
(27)

式(27)對時間導(dǎo)數(shù)為

(28)

將式(26)代入(25),將式(28)可改寫為

(29)

其中

(30)

ξ1為正常數(shù),由式(19)和(30)將(29)改寫為

≤-2min[λmin(k1),λmin(k2)-ξ1,

≤-ρV+ω

(31)

其中

(32)

5 仿真結(jié)果

本文選取PUMA560機械臂為控制對象,關(guān)節(jié)均為旋轉(zhuǎn)型關(guān)節(jié)。為了建模方便且易于分析,故只考慮機械臂前三個關(guān)節(jié)。各連桿質(zhì)量,桿長,轉(zhuǎn)動慣量見表1。給定機械臂期望軌跡:xd=[sin(0.5t),cos(0.5t),0.5cos(0.5t)]T。總擾動:τd=τ0+τf,其中τ0如式(33)所示。摩擦項參數(shù):φ1=φ2=0.2,φ3=0.5,γ1=1,γ2=γ3=0.5。控制器參數(shù):k1=diag[90,90,90],k2=diag[100,100,100]。

表1 機械臂物理參數(shù)

(33)

通過與非線性PD跟蹤控制器式(34)進行對比,突出了本文設(shè)計控制器的良好控制性能。非線性PD控制器為

(34)

其中kp1=kp2=600,kd1=kd2=400。反步控制器與非線性PD控制器產(chǎn)生的實際信號為q=[q1,q2,q3]T,qPD=[qPD1,qPD2,qPD3]T。期望信號為qd=[qd1,qd2,qd3]T。

由圖2與圖4可以知道,存在外界干擾的情況下,非線性PD控制器在開始前2s內(nèi),對關(guān)節(jié)2、3的跟蹤性能較差。而設(shè)計的反步控制器性能優(yōu)于PD控制器,跟蹤速度快,有良好的魯棒性。圖3與圖5顯示了各關(guān)節(jié)的跟蹤誤差,由圖可以看出誤差均收斂在原點附近且所提控制器收斂速度快于PD控制器。

圖2 關(guān)節(jié)位置跟蹤

圖3 位置跟蹤誤差

圖4 關(guān)節(jié)速度跟蹤

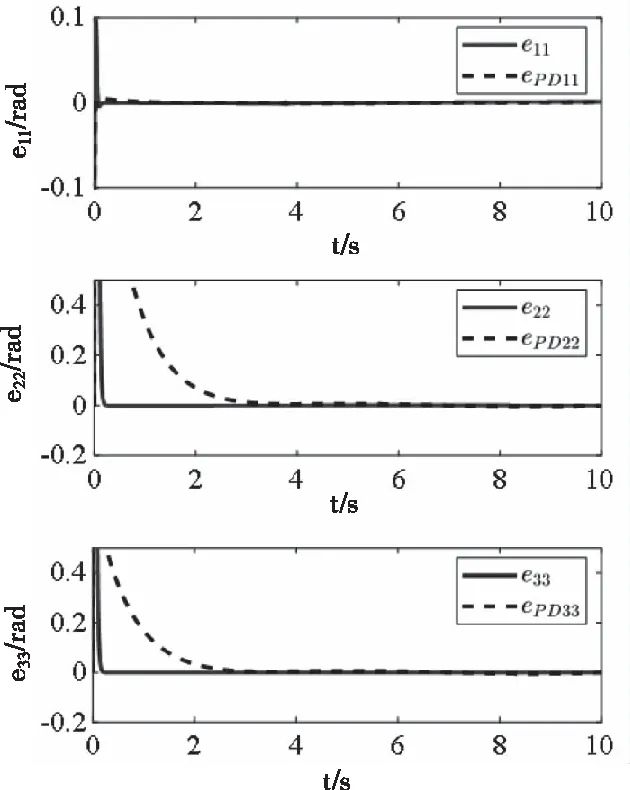
圖5 速度跟蹤誤差

用以下誤差指標比較反步控制器與非線性PD控制器的跟蹤響應(yīng)特性,比較結(jié)果如表2所示。由表可知,本文設(shè)計控制器控制性能優(yōu)于PD控制器且誤差更小。各指標如下:

表2 指標對比

由圖6可知,輸入力矩為合理光滑曲線。在圖7中,觀測器可以快速地跟蹤外部擾動,較準確的獲得了擾動估計值且一定程度上提高了系統(tǒng)的抗干擾能力。

圖6 關(guān)節(jié)輸入力矩

圖7 關(guān)節(jié)擾動觀測

6 總結(jié)

本文針對機械臂的精確軌跡跟蹤問題,提出一種帶有擾動觀測器的機械臂自適應(yīng)魯棒軌跡跟蹤控制策略。由于反步法具有較好的不確定性處理能力,因此通過反步法對系統(tǒng)設(shè)計控制律,提高了系統(tǒng)的跟蹤精度。采用擾動觀測器觀測系統(tǒng)所受擾動以獲取其估計值,并且設(shè)計一種自適應(yīng)律更新觀測器增益,較好的抑制了擾動對系統(tǒng)跟蹤性能的影響,提高了系統(tǒng)的魯棒性。利用李雅普諾夫穩(wěn)定性理論對整個閉環(huán)系統(tǒng)進行穩(wěn)定性分析,證明了系統(tǒng)半全局漸近穩(wěn)定。通過適當(dāng)選擇設(shè)計參數(shù)保證跟蹤誤差在有限時間快速收斂到原點附近。通過與非線性PD控制器對比,仿真結(jié)果表明了所提方法的跟蹤速度與精度均優(yōu)于PD控制器,驗證了設(shè)計控制器良好的跟蹤性能。