基于改進A*算法的變電站智能巡檢機器人路徑優化方法研究

連興文，朱旭東，陳云海，王少楠

（中國南方電網有限責任公司超高壓輸電公司昆明局，云南昆明 650000）

近年來，隨著智能電網[1]的不斷推廣與普及，我國的電力規劃取得了長足發展。而變電站智能化作為電網智能化的重要組成部分，也逐漸在智能巡檢[2]領域嶄露頭角。傳統的人工巡檢方式存在效率較低、耗費人力成本及容易引發安全問題等缺點，因此采用巡檢機器人進行智能巡檢的方式已成為變電站智能化的主流發展方向。

若要變電站智能巡檢機器人實現高質量巡檢，則需一種高效率和高精確度的路徑優化算法[3]。針對現實場景下存在的路況環境復雜多變及周圍工作人員干擾等情況，可采用智能算法[4]規劃出一條優異路徑，以此達到高效率巡檢的目的。目前常用的啟發式智能[5]路徑優化算法為傳統A*算法[6]，該算法在周圍環境簡單的情況下通常具有較好的路徑規劃能力。但在實際復雜多變的變電站環境下，其規劃出的路徑可能較長且不平滑，甚至可能存在碰撞。為解決上述問題，該文從規劃搜索空間及優化啟發函數兩個角度對傳統A*算法進行了優化提升。一方面將機器人在柵格中的運動方向擴展為24 鄰域，另一方面在啟發函數中引入了碰撞威脅代價這一影響因素，進而實現了最終規劃的路徑完整、平滑，且距離較短，并有效解決了巡檢過程中的碰撞問題。

1 基于改進A*算法的路徑優化

1.1 機器人巡檢環境建模

在進行變電站智能巡檢機器人路徑優化的研究中，首先需要將巡檢場景加以抽象。即通過傳感器獲取周圍環境信息，并對此進行建模，以形成巡檢環境地圖。柵格地圖法[7-8]憑借其建模魯棒性強、表達直觀清晰等優勢，目前已被廣泛應用于機器人路徑規劃算法的研究之中。

該文在對機器人巡檢環境進行建模時，采用單位長度的柵格地圖來表示巡檢機器人周邊的環境狀況信息，具體如圖1 所示。該方法將智能機器人的巡檢環境表示為多個具有相同尺度的方形網格，同時根據環境的阻塞情況將網格區分為兩種不同的狀態，分別是通暢與阻塞狀態。圖中空白區域網格表示該區域平坦，巡檢機器人可順利通過，即通暢狀態；黑色區域網格則表示該區域擁堵，巡檢機器人將會遇到障礙物，即阻塞狀態。

圖1 柵格地圖

為方便后續路徑優化算法的研究，該文對機器人的具體運動巡檢信息做出如下規定：1）智能機器人巡檢的整個過程中，變電站周圍的環境信息保持不變，即柵格地圖固定；2）如圖2 所示，當巡檢機器人周圍不存在障礙物時，其可按照上、下、左、右、左上、左下、右上和右下共8 個方向移動。且智能機器人在巡檢的過程中，可忽略其自身高度信息的影響。

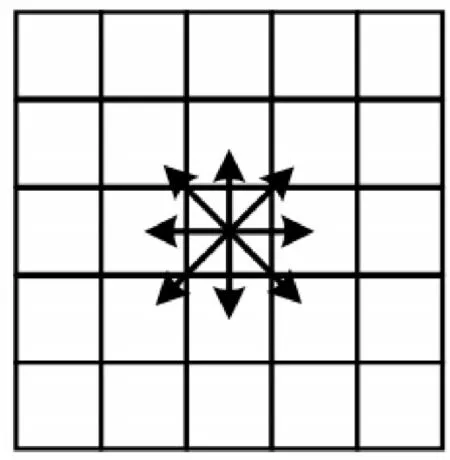
圖2 機器人運動方向

1.2 A*路徑優化算法

在路徑優化領域的研究中，A*算法由于具有較強的靈活性及對周邊多變環境的高度適應性而備受關注[9-12]。從本質上來看，該算法歸屬于人工智能領域，其實現了傳統BFS 算法(Breadth-First-Search)[13]和Dijkstra 算法[14]的巧妙結合，從而表現出了更為優異的路徑規劃性能。A*算法對應的啟發函數可描述為：

式中，函數G(n)表示為物體從路徑起點到當前位置節點的實際運動距離，即從路徑起點至節點n所需的實際代價值，在單位距離標度準則下，物體此刻位置距離起點越遠，G(n)的值便越大；相應的，函數H(n)則表示物體從路徑起點至當前位置節點的運動距離估計值。由此可見，啟發函數F(n)包含了實際運動距離與估計運動距離兩部分信息。

基于上述介紹可知，函數H(n)代表了物體運動距離的估計值，因此A*算法需選擇一個有效的距離評估公式來確定H(n)的大小。常用的距離評估函數包括歐氏距離[15]與曼哈頓距離[16]。

歐氏距離確定了n維空間中兩個孤立點p和q間的真實距離，其又被稱為歐幾里得距離，具體的數學符號可描述為：

在常見的二維平面中，對于點(x1，y1)和點(x2，y2)，二者間的歐氏距離可由式（2）改寫為：

由式（3）可知，二維平面中兩點間的歐氏距離即二者間的平面幾何距離。

曼哈頓距離從坐標軸的角度對點之間的距離做了定義，在n維空間下，其可描述為兩個孤立點在n維坐標軸上距離差的總和，具體數學實現如下：

對于點(x1,y1)和點(x2,y2)，二者間的曼哈頓距離則可由式（4）改寫為：

由式（5）可知，二維平面內的曼哈頓距離為直角坐標系中兩個點在坐標軸上投影的距離之和。

確定了距離評估算法后，便可依據啟發函數進行迭代搜索過程。在具體的算法實現過程中，主要依靠對OPEN 表與CLOSE 表的維護。其中，OPEN 表主要用于存放被運動物體發現但還未對其進行搜索的節點信息，而CLOSE 表則主要存放運動物體已經到達且搜索過的節點信息。基于這兩個表并依據啟發函數，A*算法便會不斷朝著趨近目標路徑的方向進行迭代更新，從而實現最優的路徑規劃。其具體的路徑規劃過程，如圖3 所示。

圖3 A*算法路徑規劃過程

1.3 變電站機器人智能巡檢

在傳統靜態環境中，A*算法能有效求得兩點間的最優路徑規劃距離。然而在變電站具體巡檢環境的應用背景下，由于場景的復雜性約束，傳統A*算法并不能表現出最優異的性能，因此需要對其進行改進。該文從規劃搜索空間及優化啟發函數兩個角度對該算法進行優化提升。

當機器人在柵格中按照圖2 所示方向運動時，其周圍最多存在8 個鄰域搜索點，且這些點可能為通暢或阻塞狀態。基于此，機器人運動的方向角度被限制在了π/4 的整數倍內，因此搜索迭代的行進方向也被限制在了較小的鄰域范圍內。為解決此問題，并擴展機器人運動搜索區域，該文在每個節點僅有8 個鄰域的基礎上，擴展節點至周圍的24 個鄰域，從而增加了搜索范圍。

變電站智能巡檢機器人在巡檢過程中，不僅要求符合軌跡特性的最短路徑，同時也要求巡檢過程中不會與周圍障礙物發生碰撞，且可保持一定的安全距離。因此，為了防止機器人在最短路徑下與障礙物發生碰撞，需對A*算法原始啟發函數進行相應的優化。即在原始啟發函數的基礎上引入碰撞威脅代價，并賦予一定的加權系數后，能獲得改進的啟發函數為：

其中，gp(n)為巡檢機器人已走過路程的路徑代價，gc(n)為在巡檢途中與障礙物發生碰撞的代價，而Wp和Wc則為引入的加權系數，分別表示路徑與碰撞代價在實際代價中所占的比例。

路徑代價gp(n)可由機器人運動路徑節點中距離的累加值表示：

其中，巡檢機器人每運動一步的路徑代價d的大小為其在柵格中的搜索步長。

該文通過關鍵約束點與障礙物的距離來定義碰撞代價gc(n)，定義Cn為當前節點下的碰撞威脅，dmin為關鍵約束點到障礙物的距離最小值，dsafe為設定的安全距離，則每個節點下的碰撞威脅Cn可表示為：

根據式（8），可得到碰撞代價gc(n)為巡檢機器人運動途中發生的所有碰撞威脅總和，即：

綜上所述，優化改進后啟發函數的實際代價便由路徑及碰撞代價共同決定，且通過設定路徑代價和碰撞代價占比大小的不同，便可達到更優的路徑規劃效果。

依據上文改進A*算法的設計，該文所提算法具有復雜環境條件下的適應性與穩定性。綜合這兩個角度的優化點，能夠確定出該算法的整體實現流程如圖4 所示。

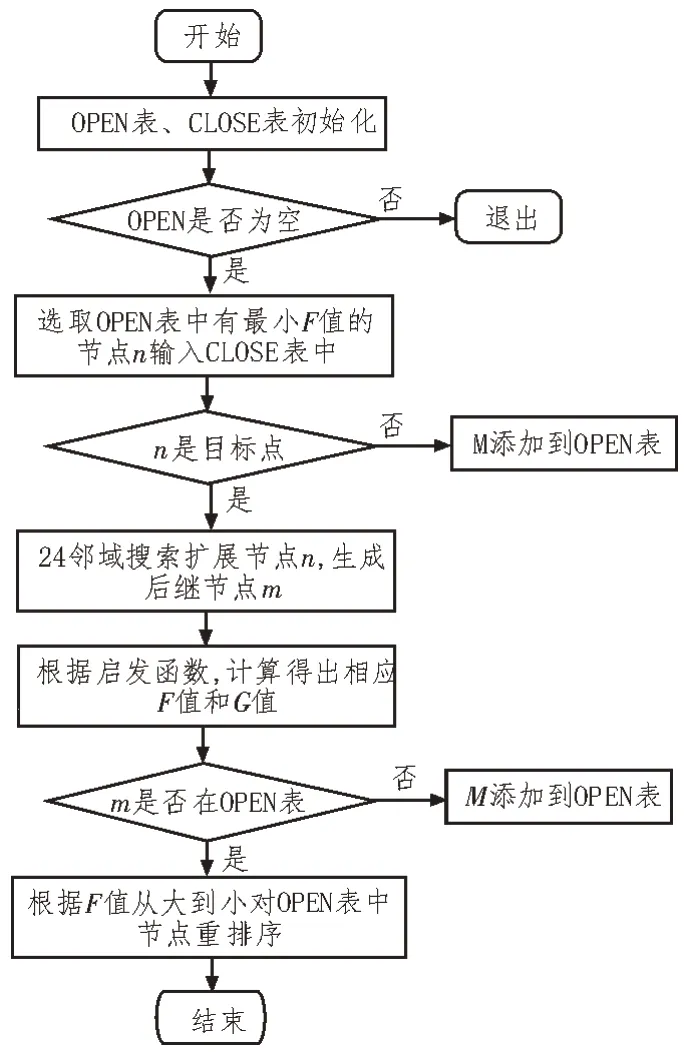
圖4 該文算法實現流程

2 驗證與分析

仿真測試在PC 端的Matlab 平臺上進行，軟硬件環境參數如表1 所示。

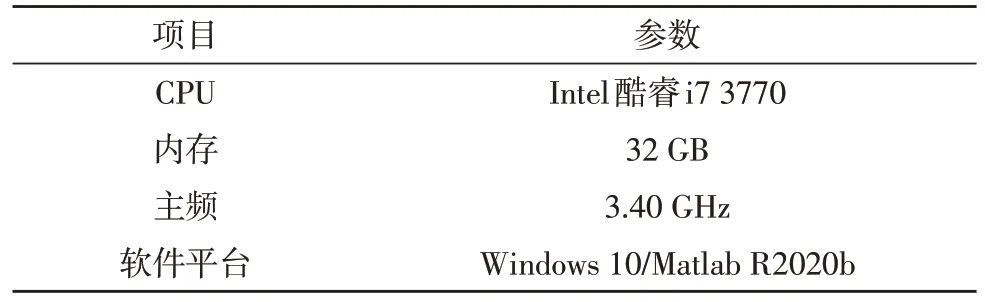
表1 實驗軟硬件環境配置

該文分別對傳統A*算法與所提算法進行路徑規劃對比，具體的仿真環境限定為50×50 大小的柵格地圖。在此環境下，分別進行兩次不同運動距離的路徑規劃仿真，仿真結果如圖5-6 所示。

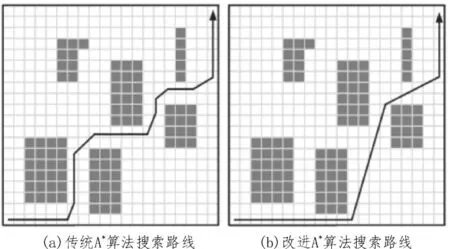
圖5 第1組實驗路徑仿真

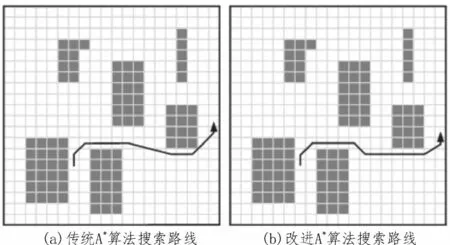
圖6 第2組實驗路徑仿真

由圖可知，該文所提算法在實驗仿真中規劃出的路徑具有轉折次數少、線路平滑及距離較短等多種優勢，同時其規劃路徑有效規避了障礙物的影響。

為了從數據層面進一步測試該算法的性能，通過設定不同尺寸的柵格地圖，來直接測定路徑尋優的搜索時間與規劃路徑的長度，具體實驗結果如表2-3 所示。

表2 路徑規劃搜索時間比較

由表2 可知，相比于傳統A*算法，該文算法的尋優時間較少，且這種時間差異隨著柵格地圖尺寸的增大而變得更加明顯。當柵格地圖的單邊尺寸增加到100 時，該文算法的搜索時間得到了顯著優化。

由表3 可知，該文算法規劃出的最優路徑距離低于傳統A*算法，這表明改進后的算法具有更優異的規劃性能。

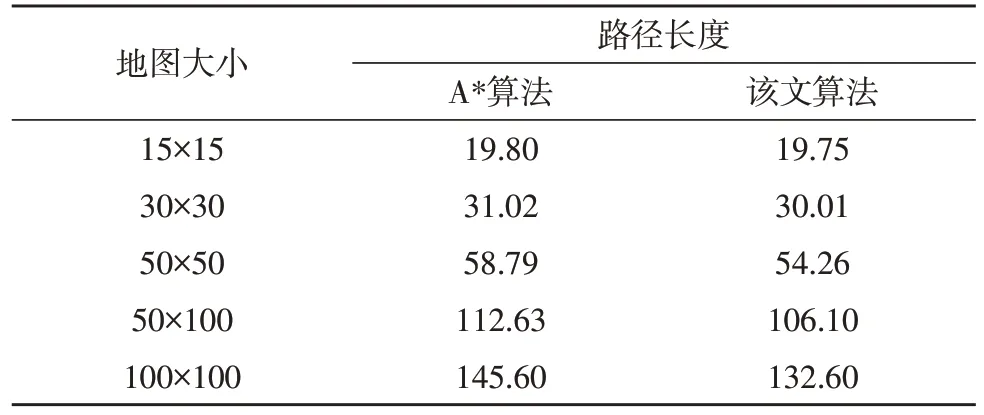
表3 規劃路徑長度比較

3 結束語

該文從擴展尋優搜索鄰域及改進啟發函數兩個角度對傳統的A*算法進行了改進，通過24 鄰域進行啟發式搜索，提高了路徑規劃路線的平滑性、縮短了距離。同時，針對無法有效避障等問題，引入碰撞威脅代價對原有啟發函數進行了改進。實驗仿真結果充分證明了該文所述的改進算法具有更為優越的綜合性能。