基于地形斷面參數辨識的泵站水動力模型研究

柯 仁,秦 鍇

(1.深圳市水務規劃設計院股份有限公司,廣東 深圳 518001;2.中國建筑第四工程局有限公司,廣州 510000)

0 引 言

在社會和經濟發展以及保障社會健康等諸多層面上,水資源具有不可替代的重要地位[1]。我國作為農業大國,由于特殊的地理和氣候條件,同時面臨著水資源時空分布不均、供需矛盾突出、水質惡化和水資源利用率低的問題,使社會經濟發展受到水資源的強烈制約。南水北調工程是解決華北地區嚴重缺水問題的重要戰略,經過多年的探索、規劃和研究,長江流域規劃出東西中3條調水線路[2]。其中,河道被用作送水載體,泵站被用作主要控制結構,從低洼水源區開始,通過泵站的提水功能,將水輸送至地勢較高的接收區[3]。近年來,隨著水資源調度理論和計算機技術的快速發展,研究人員試圖對各種引水工程進行自動化和智能化調度,以保證工程的安全和穩定[4]。由于地形參數的不足以及水流撞擊等諸多干擾因素,將會帶來調水系統的計算難題[5]。因此,有必要研究泵站的輸水特性,以實現準確的水力控制,并找到一種在地形數據缺失的情況下描述流量的方法,從而消除模擬建模對河流地形的依賴[6]。

鑒于此,本文提出一種基于數字高程模型(Digital Elevation Model,DEM)和敏感性分析方法,來優化現有水動力模型,以期優化調水工程決策問題。

1 面向地形數據缺失的泵站水動力計算模型優化

1.1 考慮水力損失和河道蓄量的一維水動力快速計算模型

一維流體動力學模型易于構建、計算快速且準確,可用于傳感和計算水流狀態。在輸水過程中,水流的摩擦和沖擊可能導致水力損失,泵站的調節會導致水道的蓄量變化[7]。此外,包括降雨、非監督流入和排水等干擾,可能會使水道中的水流難以控制。鑒于此,本此次研究將采用一維水動力模型,分析河道水力的運動規律[8]。圖1為水力特性分析示意圖。

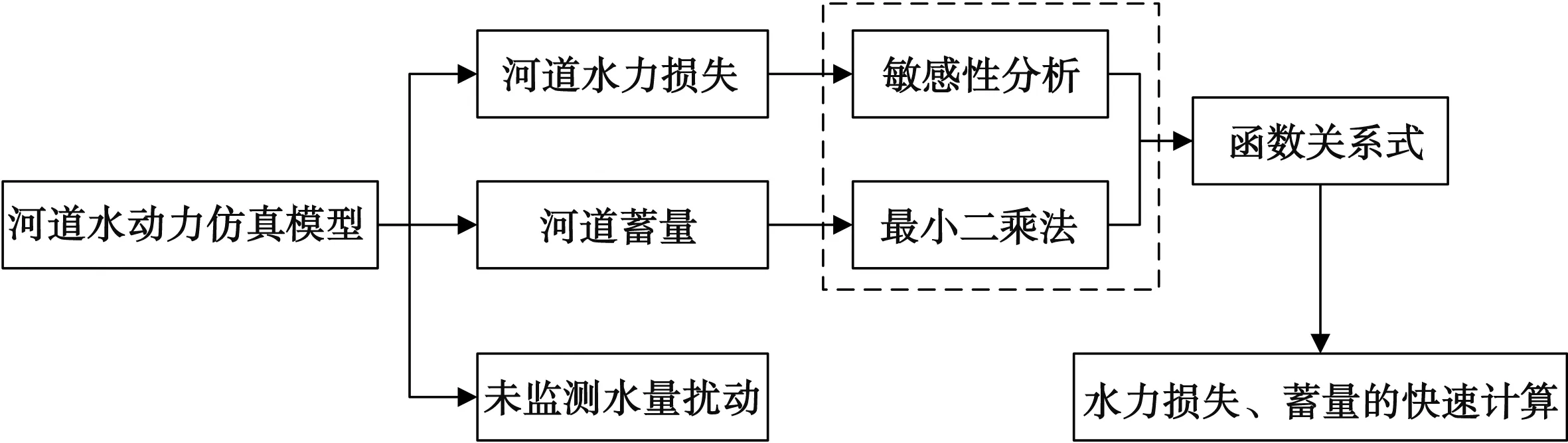
圖1 水力特性分析示意圖

明渠一維流體運動的基本方程是Saint-Venant方程。為了獲得明渠的流體動力學模型,必須添加邊界條件,才能構建一個閉合形式的方程組[9]。設置邊界約束時,一般從流量角度、水位角度或者兩者關系角度出發。第3種邊界條件因可能導致計算不穩定,而難以將水位關系應用于上游的外部邊界[10]。因此,在邊界條件上,上游和下游有5種流體流動模型。水力損失以及河道蓄量可以借助邊界條件的組合實現計算。圖2為河道水力損失計算示意圖。

圖2 河道水力損失計算示意圖

河道水力損失的第一種方法是通過上游流量、下游水位作為邊界條件,以實現對一維穩定水流進行建模,然后從下到上分級求解水面線,計算水流的水力損失。第二種是通過水流的上游水位和下游流量作為邊界條件來模擬一維穩定水流,然后從上到下分級求解水面線,計算水流的水力損失。考慮到河道蓄量的計算便利性,研究采用一維恒定流量模型來計算河流上下游的流量[11-12]。

在供水渠的運行過程中,難監測、不可控的水量擾動會給河道蓄量計算帶來計算偏差。為了準確求解水量,研究提出一種將水平衡與水力特性分析相結合的新方法來估計通道中的非監測湍流,公式如下:

(1)

1.2 基于DEM和LH-OAT的地形斷面參數識別模型優化

水流橫截面的幾何輪廓對河道的流體動力學模擬至關重要。通常,測量容器用于測量河流橫截面的幾何形狀,并通過插值處理該區域,以描述整個河道的地形。由于部分河道地形水文條件惡劣,水動力數值模擬模型難以建立。為了解決這個問題,研究使用觀測數據驅動方法,建立一個未映射的河流水動力學模型[13]。在該模型中,利用水下DEM數據,對河道中的水下地形進行梯形綜合處理,并基于LH-OAT全局靈敏度分析模型識別關鍵元素。通過粒子群算法在地形資料缺失情況下描述河流地形,從而實現更準確的水動力描述。圖3為地形概化過程示意圖。

圖3 地形概化過程示意圖

從圖3可知,人工開挖明渠流道的橫截面具有對稱性和規律性。為了滿足一般穩定性、最小河道、最小開挖量,河流斷面的幾何形狀通常采用等腰梯形。但如果用等腰梯形來直接擴展橫截面,則其對于斷面真實模擬度將減弱。

DEM由一系列不同類型的數據空間分布組成,其中高度用于表示表面特征,垂直坐標系用于描述高度空間。利用開源DEM數據,可以獲得水下地形的幾何信息,且這些信息可以被推廣。圖4為LA-OAT方法流程圖。

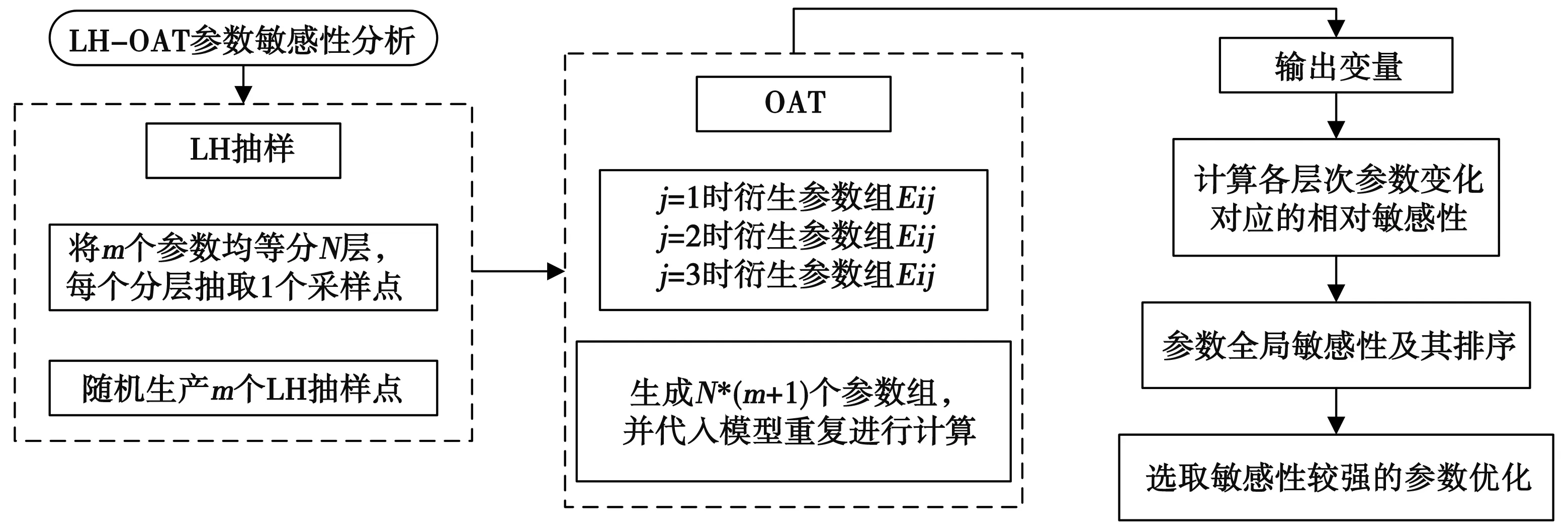
圖4 LA-OAT方法流程圖

LH-OAT(Latin hypercube-One factor at a time)算法基于Latin-Hypercube抽樣法和OAT敏感性分析組成。根據LH的抽樣概念,整個參數空間將進行堆疊,并隨機選擇每個級別。在將參數空間劃分為n個級別的情況下,產生包括P參數的一組數量為n的LH采樣參數。然后,根據OAT方法,小幅度修改LH采樣參數,以計算目標函數的變化。流體動力學模擬中,存在多種輸入元素。應用LH-OAT模型,對截面的深度和表面粗糙度進行分析,關鍵要素可以得到有效和正確的識別。本研究基于歷史觀測水位,借助粒子群優化算法,通過關鍵要素識別來確定決策變量。水位或流量計算值和實際值之間的偏差目標函數公式如下:

(2)

式中:zm、zo分別為模擬計算水位和實際水位,m;N為測量次數。

粒子群算法基于鳥類覓食行為啟發而來,因此將解空間視為鳥的運動空間。每只在運動空間中飛行的鳥都被稱為粒子,它會尋找最佳的全局位置進行求解。粒子速度和位置更新公式如下:

(3)

2 基于DEM和LH-OAT優化地形參數的水動力模型結果分析

為了驗證研究所提基于DEM和LA-OAT算法優化的水動力模型有效性,選擇南水北調工程中3個泵站作為實驗對象,其裝機臺數分別為5、4、4,單機流量分別為30、20、10m3/s。仿真時,模型邊界條件選為上游流量和下游水位,以進行恒定流水動力模擬,并計算水力損失。

從圖5可知,在0～160h的觀測時間內,起始時間的水力損失計算值49cm,水力損失實際值45cm,差值4cm,差值百分比約8.8%。當觀測時間為75h時,水力損失計算值48cm,水力損失實際值56cm,兩者差值8cm,差值百分比約14.2%。

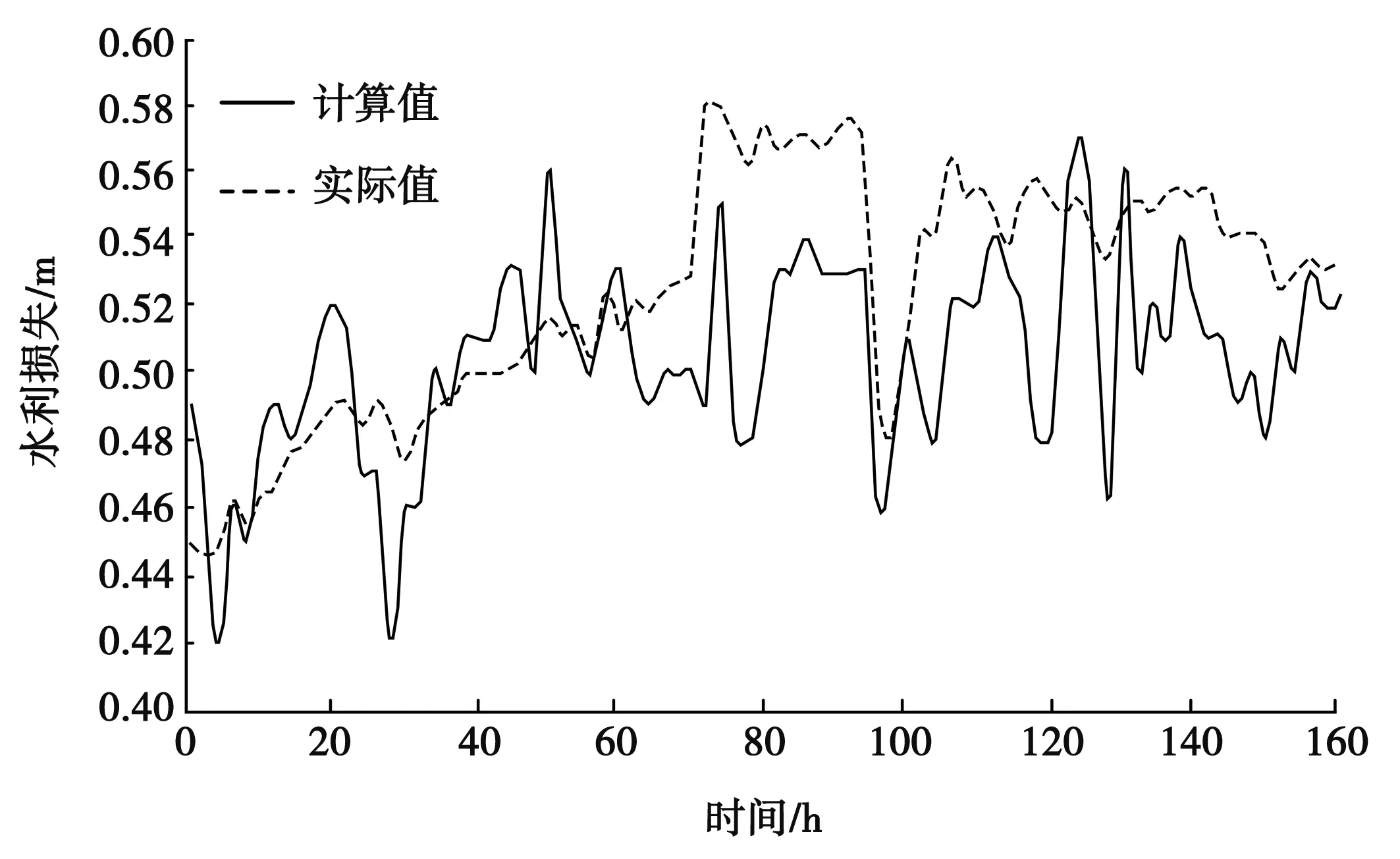
圖5 水力損失值計算值和實際值對比曲線

整體而言,水力損失計算值在46～54cm之間波動,小時內波動范圍不超過1.5cm,最小值和最大值分別為42和57cm。且在120h之后波動較為劇烈,波動頻次和幅度明顯增加。而水力損失實際值大多在48～56cm之間波動,小時內波動范圍不超過1cm,最小值和最大值分別為45和58cm。

此外,研究所提水動力模型所得水力損失值計算值曲線與水力損失實際值曲線平均誤差在3.4cm。經計算,其納什效率為0.42。因此,模擬結果較為客觀,表明該方法適用于進行水力損失的快速計算。

從圖6可知,在率定期實驗中,研究所提模型水位計算值在37.5～49.0cm之間波動,而水位觀測值在40～50.5cm之間波動。兩者波動區間差值不大,最小值和最大值分別相差2.5和1.5cm。此外,從曲線升降上看,兩條曲線僅在時間為20、60以及110h變化趨勢不一致,其余時間均具有相同走勢。驗證期實驗中,模型水位計算值和觀測值的最大差值出現在90h處,大小為5cm。兩條曲線除了在時間為70h處的增減變化不同外,其余時間點處均保持相同變化趨勢,表明研究所提模型水動力模擬結果較為精確。

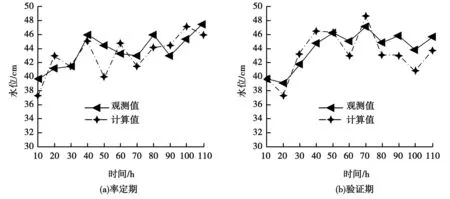
圖6 模型率定期和驗證期計算對比曲線

從表1可知,當迭代次數大于或等于40次時,橫斷面數量在取值為1～5之間時,其對應的平均誤差均低于4cm,且從迭代次數為40開始,其平均誤差穩定在3.8附近波動。當迭代次數為60,橫斷面概化數量在1～5之間變化時,其對應的模型平均誤差距離3.8差值分別為+0.03、-0.11、+0.02、-0.02、+0.02。因此,橫斷面概化數量對計算結果和優化截面的效率幾乎沒有影響。但考慮工作量將隨著推廣的數量遞增,建議減少橫斷面插值。

表1 橫斷面概化數目對模型平均誤差的影響

3 結 論

為了優化泵站調水工程調度分析,本次研究將未勘探的地形斷面河道作為研究對象,提出了一種基于DEM和敏感性分析優化的水動力模型。結果顯示,率定期水位計算值和水位觀測值差值不大,最值差值均低于3cm;驗證期水位計算值曲線和觀測值曲線幾乎保持相同變化趨勢。此外,斷面概化數目對于模型優化結果影響不大,當迭代次數為40次之后,平均誤差均低于4cm。表明研究所提模型水動力模擬結果較為精確,有助于輸水河道水力的精準控制。