單葉雙曲面與雙曲拋物面為動直線軌跡的定義

陳岱婉 陳 彥

（廣東汕頭幼兒師范高等專科學校初等教育學院，廣東 汕頭 515041）

1 引 言

在《空間解析幾何》中，二次柱面、二次錐面、單葉雙曲面、雙曲拋物面都是重要的直紋面，精準定義曲面對理解運用其直紋性意義重大. 檢索現有的文獻，對單葉雙曲面與雙曲拋物面（以下簡稱為“兩種直紋面”）的恰切定義的相關研究至今尚未發現. 文獻[1-7]是一些高等院校現行的教科書，對柱面和錐面給出嚴格定義，但對兩種直紋面就僅利用代數方法，通過方程的等價變形得出直母線方程來解釋直紋性；大部分學者對這兩種直紋面的研究，都僅涉及其上兩族直母線的存在性及它們之間的關系性質，即便有少數人研究它們作為動直線的軌跡，也是具有特殊性或缺乏揭示二次曲面的內在關聯，從而無法給出這兩種直紋面的一個較為直觀又具有二次曲面內在關聯的定義.如文獻[8]簡單探討了直紋面直母線的一般形式，籠統地證明了與三條異面直線都共面的動直線的運動軌跡是單葉雙曲面；文獻[9]從微分幾何的角度推導出單葉雙曲面上特殊截面和截線方程，并研究了單葉雙曲面可看成異面直線上動點滿足一定條件的運動軌跡問題，以驗證其直紋性；文獻[10]通過兩個特例討論滿足特殊條件動直線的軌跡就是單葉雙曲面；文獻[11]指出直紋面可視為動直線的軌跡；文獻[12]給出關于單葉雙曲面和雙曲拋物面的定義.故本文試圖從二次曲面的內在關聯出發，借鑒現行教科書中柱面和錐面的定義，給出兩種直紋面為動直線軌跡的定義，以幫助讀者對直紋面有直觀的、內在聯系的認識.

2 兩種直紋面為動直線軌跡的直觀描述及分析

2.1 預備知識

首先，考慮現行教材柱面與錐面的定義如下.

定義2.11[1]在空間，由平行于定方向且與一條定曲線相交的一族平行直線所成的曲面叫做柱面，定方向叫做柱面的方向，定曲線叫做柱面的準線，那族平行直線中的每一條直線，叫做柱面的母線.

定義2.12[1]在空間通過一定點且與定曲線相交的一族直線所成的曲面叫做錐面，這些直線都叫做錐面的母線，那個定點叫做錐面的頂點，定曲線叫做錐面的準線.

分析上述定義可知：生成柱面的動直線特質是：“一動一定”，過動點但方向不變；而生成錐面的動直線卻是：“一定一動”，一端過定點但方向改變.那么我們將要定義的生成單葉雙曲面與雙曲拋物面的動直線都是：“兩動”，過動點且方向也改變.這就是本文的難點所在，為解決該難點，我們引入兩個在本文中起關鍵作用的輔助曲面，它們能很好地揭示二次曲面之間的內在關聯.

2.2 建立平面曲線上的點與輔助曲面中的直線之間的對應關系

在空間，我們需要構建平面曲線上的點與二次錐面T1的母線或一對相交平面T2中的直線之間的對應關系，并對一些概念下定義如下.定義2.21 設過坐標原點O 且平行于平面定曲線上一點P 的從切平面[13-14]的平面，與輔助曲面Ti（i＝1，2）有兩交線，其中一條與從切平面平行的坐標軸、向徑構成左手標架，此交線稱為點P 對應的輔助曲面Ti的正母（直）線，另一條交線（與平行于定曲線上點P 的從切平面的坐標軸、向徑構成右手標架）稱為點P 對應的輔助曲面Ti的負（直）母線.

注記1：平面曲線上的點可以確定輔助曲面Ti對應的兩條母（直）線，為后面表述方便需要將其區分.為此，記正母（直）線為l＋，負母（直）線為l－（如圖1，2 所示）.

圖2

3 兩種直紋面為動直線軌跡的定義

3.1 單葉雙曲面為動直線的軌跡定義

定義3.11 在空間，與平面定曲線相交且平行于交點對應的二次錐面的正母線（或負母線）的動直線的軌跡叫做單葉雙曲面，定曲線稱為單葉雙曲面的準線，二次錐面叫做單葉雙曲面的漸近錐面，動直線中的每一條都叫做單葉雙曲面的母線（如圖3 所示）.單葉雙曲面的準線不唯一，可為下列平面曲線（其中常數a，b，c＞0）：

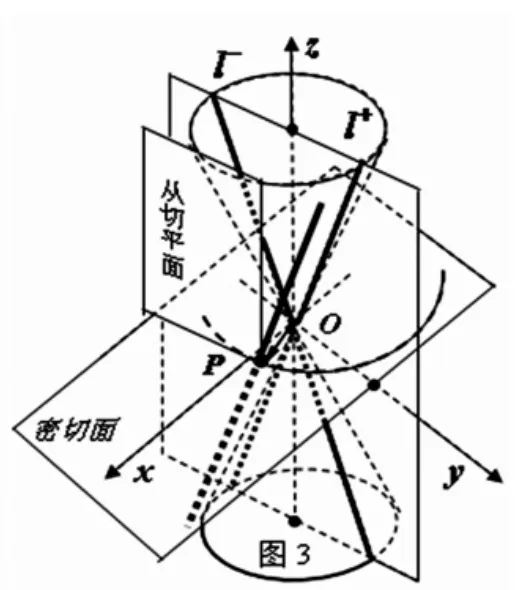
圖3

（1）腰橢圓[4，15]（2）雙曲線（3）雙曲線

證明 Ⅰ.先證與平面定曲線相交且平行于交點對應的二次錐面T1的正母線的動直線的軌跡是單葉雙曲面.

考慮到由于平面定曲線將作為母線，動直線須沿它運動，故在平面定曲線上任取一點時，動直線必過該點（下一個定義3.21 也相應雷同）.故有下面：（1）當準線為腰橢圓時Σ1，

設P（x0，y0，0），則過點P 的從切平面為

故過點O 且平行于點P 的從切平面的平面α 為

ⅱ）其次，求平面α 與錐面T1的交線.

聯立方程（1）、（3），得平面α 與錐面T1的交線為

可得交線有兩解，即為點P 對應的二次錐面T1的正、負母線.若取z＝abc 代入（4），求得兩母線的方向數為

由定義2.21 知，點P 對應的正母線l＋的方向數為－a2y0:b2x0:abc，點P 對應的負母線l－的方向數為－a2y0:b2x0:（－abc）.

ⅲ）最后，求以腰橢圓Σ1為準線，過點P∈Σ1且方向平行于點P 對應的二次錐面T1的正母線的動直線的軌跡.

設動直線的參數方程為

聯立（5）、（6）消去x0，y0，t 并整理可得

故該軌跡為單葉雙曲面（如圖4 所示）.命題得證.

圖4

（2）當準線為雙曲線Σ2時，

設Q（0，y0，z0），則過點Q 的從切平面為

故過點O 且平行于點Q 的從切平面的平面β 為

ⅱ）其次，求平面β 與錐面T1的交線.

聯立方程（1）、（7），得平面β 與錐面T1的交線為

可得交線有兩解，即為點Q 對應的二次錐面的正、負母線.若取x＝abc 代入（8），求得兩母線的方向數為

由定義2.2.1 知，點Q 對應的二次錐面的正母線l＋的方向數為abc:b2z0:c2y0，點Q對應的二次錐面的負母線l－的方向數為－abc:b2z0:c2y0.

ⅲ）最后，求以雙曲線Σ2為準線，過點Q∈Σ2且方向平行于點Q 對應的二次錐面的正母線的動直線的軌跡.設動直線的參數方程為

聯立（9）、（10）消去y0，z0，t 并整理可得

故該軌跡為單葉雙曲面.命題得證.

（3）當準線為雙曲線Σ3時，

與（1）、（2）中的ⅰ）、ⅱ）類似，一旦W（x0，0，z0）∈Σ3，便可求得點W 對應的二次錐面的正母線l＋的方向數為a2z0:abc:c2x0，點W 對應的二次錐面的負母線l－的方向數為a2z0:（－abc）:c2x0.

ⅲ）最后，求以雙曲線Σ3為準線，過點W∈Σ3且方向平行于點W 對應的二次錐面的正母線的動直線的軌跡.設動直線的參數方程為

聯立（11）、（12）消去x0，z0，t 并整理可得

故該軌跡為單葉雙曲面.命題得證.

Ⅱ.對于與平面定曲線相交且平行于交點對應的二次錐面T1的負母線的動直線的軌跡是單葉雙曲面，證明過程完全與Ⅰ情況雷同，這里從略.

注記2：在該定義3.11 中，與平面定曲線相交且平行于交點對應的二次錐面的正母線或負母線的動直線的軌跡正好是對應文獻[16]所定義的單葉雙曲面的直母線u，v 族.

3.2 雙曲拋物面為動直線的軌跡定義

定義3.21 在空間，與平面定曲線相交且平行于交點對應的一對相交平面T2的正母線（或負母線）的動直線的軌跡叫做雙曲拋物面，定曲線稱為雙曲拋物面的準線，這對相交平面叫做雙曲拋物面的漸近平面，動直線中的每一條都叫做雙曲拋物面的母線（如圖5所示）.雙曲拋物面的準線不唯一，可為下列平面曲線（其中常數a，b＞0，c≠0）：

圖5

證明 Ⅰ.先證與平面定曲線相交且平行于交點對應的一對相交平面T2的正母線的動直線的軌跡是雙曲拋物面.

（1）當準線為拋物線Γ1時，

設P（0，y0，z0），則過點P 的從切平面為

故過點O 且平行于點P 的從切平面的平面α 為

ⅱ）其次，求平面α 與一對相交平面T2的交線.

聯立方程（2）、（13），得平面α 與一對相交平面T2的交線為

可得交線有兩解，即為點P 對應的相交平面T2的正、負直線.若取y ＝-b 代入（3.12），求得兩直線的方向數為

由定義2.2.1 知，點P 對應的一對相交平面的正直線l＋的方向數為點P 對應的一對相交平面的負直線l－的方向數為

ⅲ）最后，求以拋物線Γ1為準線，過點P∈Γ1且方向平行于點P 對應的相交平面T2的正直線的動直線的軌跡.

設動直線的參數方程為

聯立（15）、（16）消去y0，z0，t 并整理可得

故該軌跡為雙曲拋物面（如圖6 所示）.命題得證.

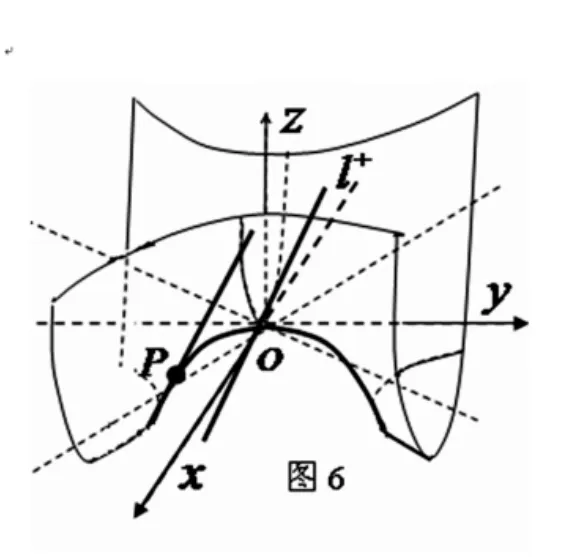
圖6

（2）當準線為拋物線Γ2時，

設P（x0，0，z0），則過點Q 的從切平面為

故過點O 且平行于點Q 的從切平面的平面β 為

ⅱ）其次，求平面β 與相交平面T2的交線.

聯立方程（2）、（17），得平面β 與相交平面T2的交線為

可得交線有兩解，即為點Q 對應的一對相交平面T2的正、負直線. 若取x＝a 代入（18），求得兩直線的方向數為

由定義2.2.1 知，點Q 對應的正直線l＋的方向數為點Q 對應的負直線l－的方向數為

ⅲ）最后，求以拋物線Γ2為準線，過點Q∈Γ2且方向平行于點Q 對應的一對相交平面的正直線的動直線的軌跡.

設動直線的參數方程為

聯立（19）、（20）消去x0，y0，t 并整理可得

故該軌跡為雙曲拋物面.命題得證.

Ⅱ.對于與平面定曲線相交且平行于交點對應的一對相交平面的負母線的動直線的軌跡是雙曲拋物面，證明過程完全與Ⅰ情況雷同，這里從略.

4 結論

本文在現行《空間解析幾何》教材及文獻的相關內容的基礎上給予擴展，從二次曲面的內在關聯出發，分別利用漸近錐面或一對相交平面找到單葉雙曲面與雙曲拋物面的直母線的運動軌跡，從而給出這兩種直紋面為動直線的軌跡定義.在本定義中，若將動直線方向固定，則得到柱面，若動直線一端經過固定點，則得到錐面，故它具有一般性，可視為柱面和錐面定義的推廣.我們的后續工作是研究單葉雙曲面與其漸近錐面有關性質的比較.