錨桿支護對土質隧道圍巖位移影響的數值分析

閆茂龍

（山東北匯建設工程有限公司，山東菏澤 274000）

0 引言

錨桿在隧道支護體系中是一種很有效的支護方式[1-2]，合理確定該支護參數將直接影響到隧道圍巖的穩定性。通常錨桿的加固效應主要有4 種：懸吊效應、增強效應、成拱效應和內壓效應[3]。其中懸吊效應是指錨桿把由于開挖、爆破等造成的松動巖塊穩固（懸吊）在穩定巖層上，防止破碎巖塊冒落的效應[4]。錨桿支護參數主要是根據設計者的經驗、數值計算、相關試驗以及工程規范等進行選取[5]。主要利用錨桿的懸吊效應并借助離散元法模擬錨桿支護參數（長度、間距）對隧道圍巖穩定性的影響，可為隧道防護工程及錨桿優化設計提供參考。

本文基于離散單元法，從細觀角度研究錨桿支護對土質隧道圍巖位移的影響。從前期學者的研究成果來看，離散單元法已用于分析圍巖的失穩機制[6-8]。A.Fakhimi 等[9]用離散單元法模擬了巖石中圓形洞體的開挖問題，分析了洞周圍巖的破壞機理。朱偉等[10]已對盾構隧道垂直土壓力松動效應進行顆粒流模擬研究。蔣明鏡等[11]也已對考慮尾隙的盾構隧道土壓力進行了離散元數值分析。

本文采用離散單元法模擬錨桿支護對隧道圍巖位移的影響，并分析了錨桿不同長度、不同間距時隧道上方圍巖豎向位移的變化情況。

1 隧道數值計算模型

數值模擬中，圍巖參數取用參考文獻[12]，定義上下左右4 道墻體（法向、切向剛度分別為2×108N/m、1.5×108N/m），創建寬60 m，高80 m 的模型箱，在模型箱內分3 層生成156 741 個圓形顆粒（密度為2 630 kg/m3）制備砂土試樣，試樣的生成過程如圖1 所示。

圖1 顆粒流模型的試樣生成

隧道數值模型如圖2 所示，開挖斷面位于第二層試樣的中間（直徑為6 m，埋深35.5 m）。模擬試驗過程為：刪除圓形隧道開挖范圍內的顆粒；將襯砌（厚0.4 m）處顆粒的法向、切向剛度分別改為7.8×108N/m、3.4×108N/m，另外創建該處顆粒間的平行黏結（法向、切向黏結剛度分別取2.1×1010Pa/m、0.9×1010Pa/m，法向、切向黏結強度均取1×1010Pa，pb_radius 取1）；將錨桿處顆粒的法向、切向剛度分別改為7.8×108N/m、3.4×108N/m，并將錨桿與圍巖之間的摩擦系數設為0.5，另外創建該處顆粒間的平行黏結（法向、切向黏結剛度分別取1×1012Pa/m、5×1011Pa/m，法向、切向黏結強度分別取1×1012Pa、5×1011Pa，pb_radius 取1）；再次達到自重平衡狀態后，得到隧道圍巖位移的分布規律。

圖2 隧道顆粒流模型

本文研究內容主要包括：錨桿支護對隧道圍巖位移的影響；錨桿（間距1.178 m）長度對隧道上部圍巖位移的影響，長度取0.5 m、1 m、1.5 m、2 m、2.5 m、3 m、3.5 m、4 m、4.5m；錨桿（長度3 m）間距對隧道上部圍巖位移的影響，間距取0.471 m、0.524 m、0.589 m、0.673 m、0.785 m、0.942 m、1.178 m、1.571 m、2.356 m；錨桿總長取27 m時，間距對隧道拱頂處圍巖位移的影響，間距同上（本文針對某一間距，單根錨桿長度相同）；不同錨桿總長度對應的最優間距，以及最優間距條件下的隧道拱頂處圍巖位移，總長度取9 m、13.5 m、18 m、22.5 m、27m。

2 數值模擬結果分析

2.1 隧道圍巖豎向位移

圖3為無錨桿、有錨桿（長度3 m，間距1.178 m）時隧道開挖穩定后圍巖豎向位移云圖。對比兩種情況可知，錨桿在很大程度上限制了隧道上部圍巖的豎向位移，但隨著至隧道距離的增大該影響愈加不明顯。另外，錨桿對隧道左、右、下部圍巖的豎向位移基本無影響。

圖3 隧道圍巖豎向位移云圖（單位：m）

2.2 錨桿長度對隧道上部圍巖豎向位移的影響

圖4 為隧道正上方圍巖豎向位移隨錨桿（間距1.178 m）長度的變化情況。由圖4 可知，與無錨桿情況對比，錨桿加固范圍內的圍巖豎向位移顯著降低，且錨桿越長該現象越明顯；但超出錨桿加固范圍該位移變化不大，且當錨桿長度超過一定值時隨其長度增加該位移略有增大。上述現象主要由于錨桿的懸吊作用原理引起的，即通過錨桿將軟弱、松動、不穩定的圍巖懸吊于穩定的圍巖中，以防其滑落，從而導致錨桿加固范圍內的圍巖豎向位移顯著降低；距隧道越遠圍巖越穩定，致使錨桿越長其加固范圍內的圍巖豎向位移越小；錨桿越長對圍巖的干擾范圍越大，從而引起錨桿加固范圍以外的圍巖位移略有增大。

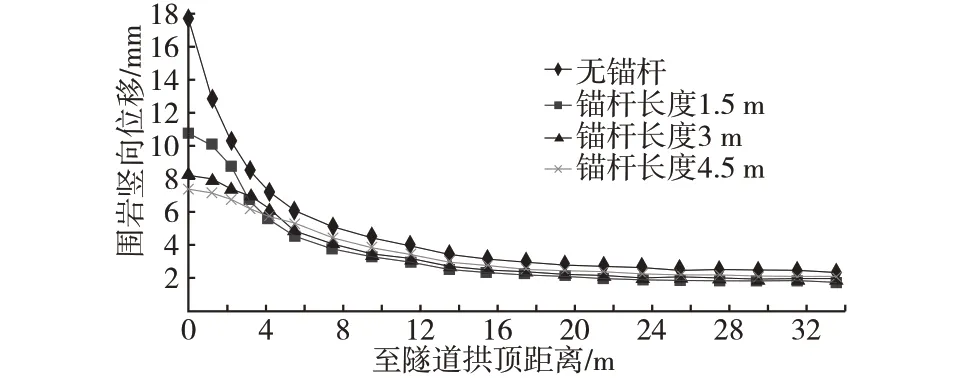
圖4 錨桿長度對隧道正上方圍巖豎向位移的影響

圖5 為隧道拱頂圍巖豎向位移隨錨桿長度的變化情況。由圖5 可知，隨錨桿長度的增加拱頂圍巖豎向位移有減小的趨勢；但錨桿長度大于3.5 m 時，該趨勢不明顯，即錨桿長度大于一定值時，隨錨桿長度的增加拱頂圍巖豎向位移基本保持不變。

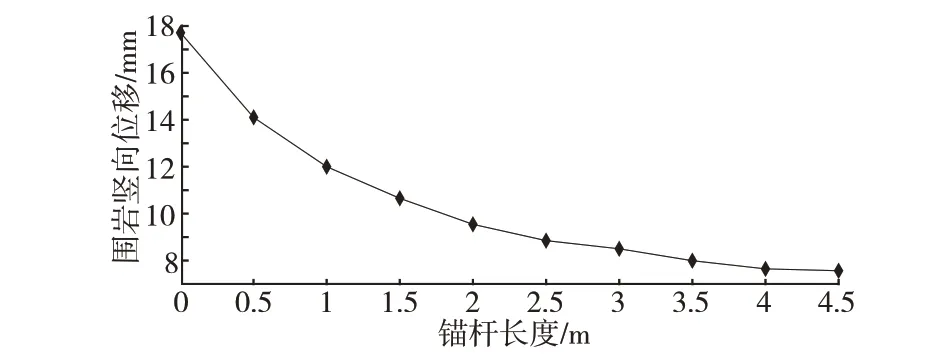
圖5 錨桿長度對隧道拱頂圍巖豎向位移的影響

2.3 錨桿間距對隧道上部圍巖豎向位移的影響

圖6 為隧道正上方圍巖豎向位移隨錨桿（長度3 m）間距的變化情況。由圖6 可知，錨桿間距區別于其長度對隧道正上方圍巖豎向位移的影響，在于不同錨桿間距對應的影響曲線之間沒有交點，即隧道正上方圍巖豎向位移始終隨錨桿間距的增大而增大。

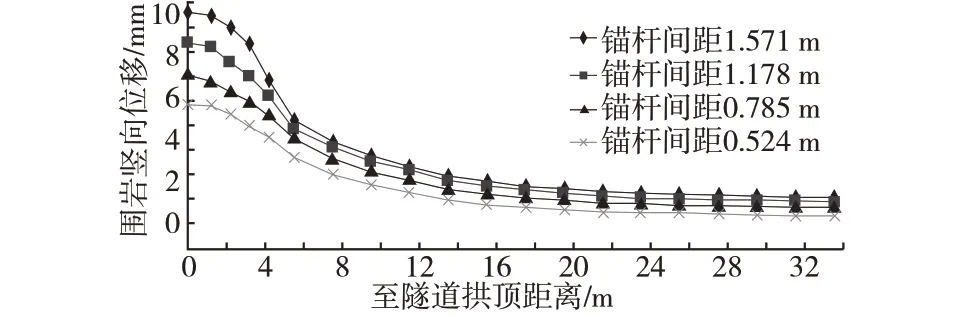
圖6 錨桿間距對隧道正上方圍巖豎向位移的影響

圖7 為隧道拱頂圍巖豎向位移隨錨桿間距的變化情況。由圖7 可知，隧道拱頂圍巖豎向位移隨錨桿間距的增加大體呈對數曲線增大。

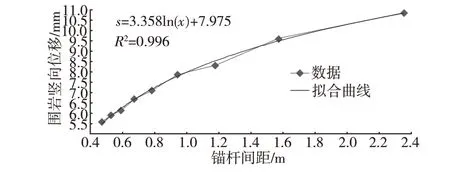
圖7 錨桿間距對隧道拱頂圍巖豎向位移的影響

2.4 固定錨桿總長度間距對隧道拱頂處圍巖豎向位移的影響

圖8 為錨桿總長取27 m 時，隧道拱頂圍巖豎向位移隨錨桿間距的變化情況。由圖8 可知，錨桿間距約為0.6 m 時，隧道拱頂圍巖豎向位移出現極小值，稱該間距為錨桿最優間距。對此解釋為：錨桿間距較小時對應其長度就較短，錨桿產生不了有效的懸吊作用，從而隧道拱頂圍巖豎向位移偏大；錨桿間距較大時對應其長度就較長，較長錨桿相應的懸吊作用隨其長度的增加而趨于穩定，此時錨桿間距的增加導致了隧道拱頂圍巖豎向位移也偏大。

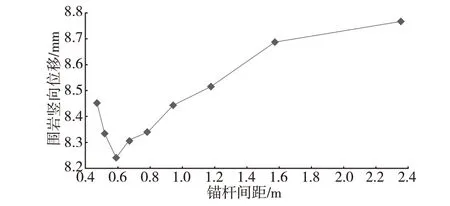
圖8 錨桿間距對隧道拱頂圍巖豎向位移的影響（錨桿總長27m）

圖9 為錨桿最優間距隨錨桿總長度的變化情況。由圖9 可知，錨桿最優間距隨其總長度的增加而減小。上述由于錨桿總長度較小時，選用單根較長的錨桿才能產生有效的懸吊作用，從而導致錨桿的最優間距較大；錨桿總長度較大時，較長錨桿相應的懸吊作用隨其長度的增加而趨于穩定，此時適當減小錨桿間距能達到降低隧道拱頂圍巖豎向位移的效果。

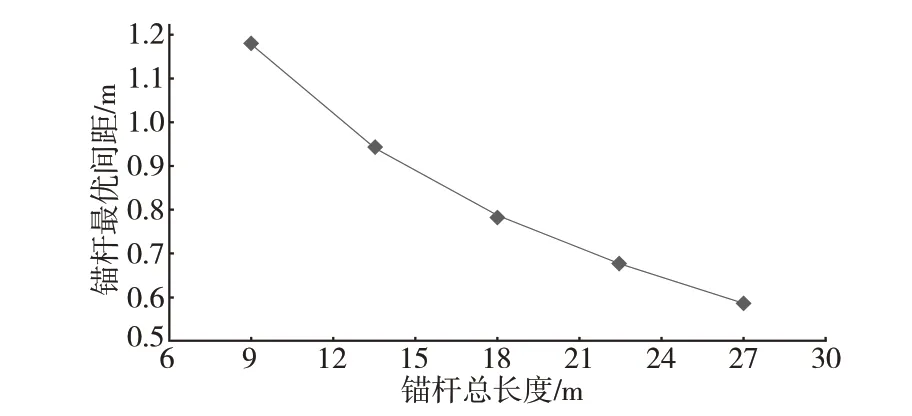
圖9 錨桿最優間距-錨桿總長度關系曲線

圖10 為錨桿間距最優時隧道拱頂圍巖豎向位移隨錨桿總長度的變化情況。由圖10 可知，在錨桿間距最優的條件下，拱頂圍巖豎向位移隨錨桿總長度的增加而減小；與錨桿間距為1.178 m 時的情況對比，兩種情況均隨錨桿總長度增加呈現拱頂圍巖豎向位移減小趨勢降低的現象，且兩種情況對應的拱頂圍巖豎向位移相差不大，說明錨桿總長度對拱頂圍巖豎向位移的影響遠大于其間距帶來的影響。

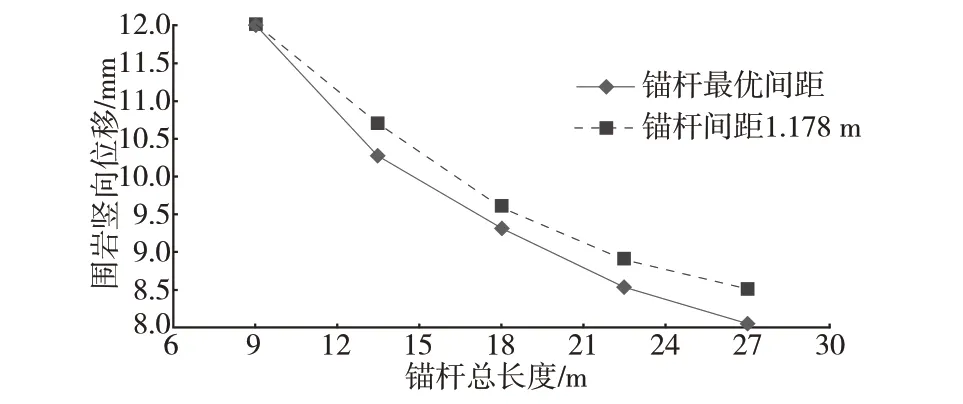
圖10 隧道拱頂圍巖豎向位移-錨桿總長度關系曲線（錨桿間距最優）

3 結論

本文采用離散單元法模擬了錨桿支護對隧道圍巖位移的影響，并分析了不同錨桿支護方式對隧道上方圍巖豎向位移的影響，得到的主要結論如下：

a）對比無錨桿情況，有錨桿支護（間距固定）在其加固范圍內隧道上方圍巖豎向位移顯著降低，且錨桿越長該現象越明顯；但錨桿加固范圍以外隧道上方圍巖豎向位移變化不大，且當錨桿長度超過一定值時隨其長度增加該位移略有增大。

b）錨桿間距固定時，隧道拱頂圍巖豎向位移隨錨桿長度的增加而減小，但錨桿長度大于一定值時，隨錨桿長度的增加該位移基本保持不變。

c）錨桿長度固定時，隧道上方圍巖豎向位移始終隨錨桿間距的增大而增大，拱頂圍巖豎向位移隨錨桿間距的增加大體呈對數曲線增大的趨勢。

d）錨桿總長度固定時，其最優間距存在，即此間距條件下隧道拱頂圍巖豎向位移最小。

e）錨桿最優間距隨其總長度的增加而減小，且錨桿間距最優時隧道拱頂圍巖豎向位移也隨其總長度的增加而減小；錨桿總長度對拱頂圍巖豎向位移的影響遠大于其間距帶來的影響。