粘彈性兩跨輸流管道的流固耦合動力特性分析★

劉 穎，王 威，夏艷波，周凌峰

(湖南交通工程學院,湖南 衡陽 421001)

輸流管道在航空、水利、核能、石油和海洋等領域有著廣泛的應用,這使得與之相關的流固耦合振動問題在近一個世紀以來受到了廣泛的關注和研究[1-7],但學者們的工作內容大部分是圍繞單跨輸流管道,對多跨輸流管道的研究很少。李寶輝等[8]以Timoshenko梁為模型,從波動的角度出發,運用波動法對管道進行了研究,借助流固耦合方程得到了波在固支、簡支和自由三種端部條件下的反射矩陣以及波在中間彈性支撐處的散射矩陣,然后以一段4 m長的簡支管道為實例驗證了波動法的正確性,最后結合上述散射矩陣,得到了分析多跨管道流固耦合振動的頻率特征方程。陰豪等[9]考慮了軸向力、液體壓力、泊松比對充液直管的影響,通過分析其模態函數的特征方程得到低頻情況下的點矩陣,然后以五跨充液直管為實例,驗證了傳遞矩陣法以及計算方法的正確性,最后分析了閥門對單跨和多跨模態頻率的影響。

本文采用Bernoulli-Euler梁模型,運用Laplace變換對多跨輸流管道的運動微分方程進行求解,提出求解多跨輸流管道固有特性的Green函數法,可為分析多跨輸流管道提供一種新的計算方法。

1 運動微分方程

如圖1所示,鉸支支撐的多跨輸流管道內流體以恒定流速流動。

管道采用Bernoulli-Euler梁模型,考慮了材料的粘彈性。位置x處、t時刻的撓度為w(x,t),其運動微分方程見式(1):

(1)

其中,EI為管道抗彎剛度;E*為粘彈性系數;w為管道橫向位移;L為管道長度;M為單位長度管道內流體的質量;m為管道單位長度質量;U為管內流體流速;Fj為中間第j個支座的支座反力,視為荷載處理,自由振動時為簡諧力,其頻率為系統自由振動頻率Ω。

引入以下無量綱量(見式(2)):

(2)

將式(1)無量綱化為式(3):

(3)

2 運動微分方程的求解

假設方程(3)的解為以下形式(見式(4)):

W(ξ,τ)=Re{η(ξ,τ)}

(4)

其中,η(ξ,τ)的計算公式見式(5):

η(ξ,τ)=X(ξ)eiωτ

(5)

將式(5)代入式(3)得式(6):

(6)

對式(6)進行Laplace變換得式(7):

(7)

解得式(8):

(8)

其中,a1的計算公式見式(9):

(9)

(10)

通過Laplace逆變換可得到式(11)—式(15):

(11)

(12)

(13)

(14)

(15)

其中,A1(ξ)～A4(ξ)的計算公式見式(16):

(16)

式(15)中ε(ξ-j)為單位階躍函數。

運用式(11)—式(15)對式(8)進行Laplace逆變換可以得到X(ξ)的Green函數形式解(見式(17)):

(17)

其中,φ1(ξ),φ2(ξ),φ3(ξ),φj(ξ)的計算公式見式(18):

(18)

為了得到管道的振型函數和頻率方程,對式(17)求導,得式(19):

(19)

從式(17),式(19)我們可以得到左端(ξ=0處)和右端ξ處的條件關系式,見式(20):

(20)

3 振型函數和頻率方程

下文以兩跨簡支輸流管道為基礎,計算兩跨簡支輸流管道的振型和頻率方程。

當n=2時,如圖1所示多跨簡支支撐輸流管道的邊界條件見式(21):

(21)

將式(21)代入式(20)整理得式(22):

(22)

解得式(23):

(23)

將式(23)代入式(17)得兩跨簡支支撐輸流管道系統振型函數的Green函數解見式(24):

(24)

記式(22)的系數矩陣為A,則輸流管道系統頻率方程的Green函數解可通過式(25)獲得:

|A|=0

(25)

4 計算結果

4.1 計算方法的驗證

為了驗證此方法的正確性,設n=2,并令粘彈性系數為零,可以得到流速等于零時一階和二階的固有頻率,經計算并與文獻[10]的結果進行換算對比,二者實質上相同。

4.2 計算結果及分析

圖2給出了α=0時兩跨簡支輸流管道的無量綱復頻率實部、虛部隨無量綱流速的變化曲線。可以看出:系統一階和二階、三階和四階的變化規律相似,一階、三階、五階與圖3所示單跨簡支輸流管道的一階、二階、三階相同,二階、四階與固-簡輸流管道(未單獨圖示)的一階二階相同。一階至五階模態的初次失穩方式均為發散失穩。隨著流速繼續增加,一階和二階虛部會無限接近三階和四級虛部,然后開始分離(未相交),且一階和二階會由發散失穩變為顫振失穩。

圖4給出了α=0.01時單跨簡支輸流管道的無量綱復頻率實部、虛部隨無量綱流速的變化曲線。可以看出:當無量綱流速為零時,系統無量綱復頻率的虛部不為零,階數越高其虛部也越大;粘彈性會使系統二階、三階的發散失穩臨界流速增大。實部為零時,系統不會立刻發散失穩,且階數越高,虛部分岔所對應的流速與發散失穩所對應流速的間距也越大。隨著流速的增加,一階虛部分岔后會再次匯合。

對比圖3,圖4發現:粘彈性會提高單跨簡支輸流管道系統的二、三階發散失穩臨界流速和一階顫振失穩臨界流速(α=0時,一、二、三階發散失穩臨界流速分別為3.14,6.28,9.42;一階顫振失穩臨界流速為6.31。α=0.01時,一、二、三階發散失穩臨界流速分別為3.14,9.41,15.71;一階顫振失穩臨界流速為6.62)。

圖5給出了α=0.01時兩跨簡支輸流管道的無量綱復頻率實部、虛部隨無量綱流速的變化曲線。可以看出:系統一階和二階、三階和四階的變化規律相似,一階、三階、五階與圖4的單跨簡支輸流管道的一階、二階、三階相同。

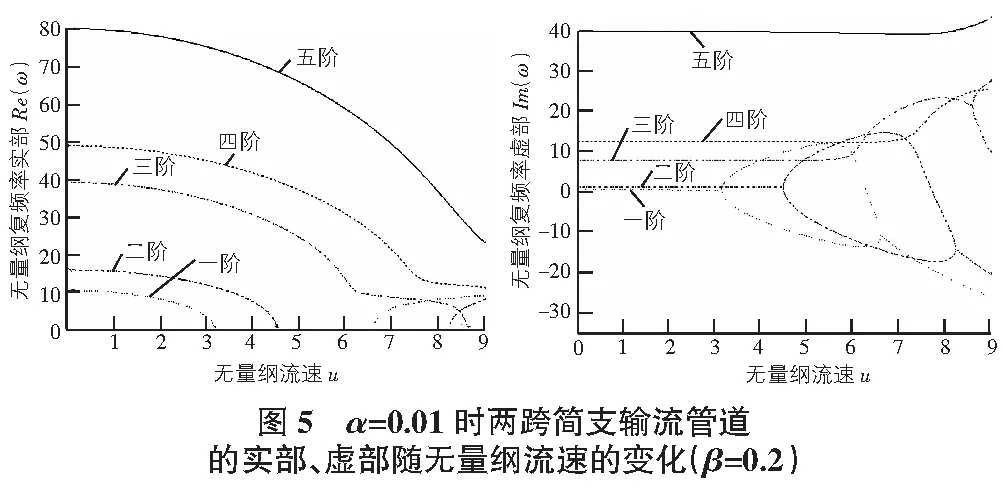
對比圖2,圖5發現:粘彈性會提高兩跨簡支輸流管道系統的三、四階發散失穩臨界流速和一、二階顫振失穩臨界流速(α=0時,一、二、三、四階發散失穩臨界流速分別為3.14,4.5,6.28,7.73;一、二階顫振失穩臨界流速為6.31,7.76。α=0.01時,一、二、三、四階發散失穩臨界流速分別為3.14,4.5,9.41,10.91;一階、二階顫振失穩臨界流速為6.61,8.23)。

5 結論

本文運用Laplace變換對多跨簡支輸流管道的運動微分方程進行求解,建立了對多跨簡支輸流管道固有特性分析的Green函數法。本文分析了單跨和兩跨簡支輸流管道無量綱復頻率隨無量綱流速的變化規律、粘彈性對無量綱流速為零時兩跨簡支無量綱復頻率實部的影響,得到以下結論:1)兩跨和單跨輸流管道的固有特性有一定關聯,兩簡支會同時含有單跨簡支和固支-簡支輸流管道的固有特性:兩跨簡支的2n-1階與單跨簡支的n階固有頻率相同,兩跨簡支的2n階與單跨固支-簡支的n階固有頻率相同。兩跨2n-1階和2n階無量綱復頻率的變化規律相似。2)粘彈性會提高系統的顫振失穩臨界流速,以及高階(階數大于跨數)的發散失穩臨界流速。3)兩跨簡支輸流管道復頻率實部高階相比于低階對粘彈性系數更為敏感。階數越高,減小至零所對應的粘彈性系數也越小,當粘彈性系數超過一定值時,系統將完全處于穩定狀態。