基于DQN算法的多微網非計劃孤島切換策略

賀旭輝,褚四虎,張 羽,張雪菲

(1.湖北省新能源微電網協同創新中心,湖北 宜昌 443002;2.三峽大學電氣與新能源學院,湖北 宜昌 443002)

0 引言

近年來,隨著可再生能源的開發和廣泛應用,分布式發電得到了大力發展[1-2]。多微網作為整合分布式電源和負荷的有效平臺,受到了眾多學者的關注。多微網可劃分為并網和孤島2種運行模式[3]。一般而言,多微網與大電網相連運行在并網模式下,此時的多微網可與大電網之間進行能量的互流互通,大電網可為多微網的電壓、頻率安全穩定提供保證。當大電網出現故障時,多微網為保證能為自身內部重要負荷提供持續可靠供電,會由并網運行非計劃性切換至孤島運行。失去大電網的功率支撐后,多微網內部分布式電源無法彌補聯絡線功率轉移時會產生巨大的功率缺額,對多微網的頻率穩定造成嚴重威脅[4-5]。

目前,針對多微網的非計劃孤島切換導致系統內部功率缺額問題的研究大致可分為補償和減載2個方向。文獻[6-7]提出利用儲能模塊跟蹤微網并離網狀態,實時補償的方式來實現微網狀態的無縫切換。文獻[8]提出一種電網相位跟蹤補償的并離網切換方式,保證微電網系統的安全穩定。然而,實時跟蹤補償在容量上局限性較大且實現成本過高,在工程實際中實用性不強。文獻[9]提出一種加速減載的優化方法,該方法考慮高比例新能源系統頻率調節特性,基于頻率變化率加速減載,以保證大功率缺額下系統的安全穩定運行。文獻[10]提出一種考慮負荷主客觀屬性的低頻減載策略,該策略利用相對熵耦合負荷的主、客觀權值對負荷進行綜合評價,以確定減載的順序。然而,上述減載策略面對復雜的多微網運行環境時自適應能力較差,在微電網環境變化場景下的減載效果并不理想。

針對現有方法的不足,提出一種基于DQN的多微網非計劃孤島切換策略。所提策略將多微網非計劃孤島切換過程中的減載決策過程描述為馬爾科夫決策過程。該馬爾科夫決策過程的狀態空間由多微網的實時負荷功率及功率缺額構成;動作空間由減載量構成。利用DQN對馬爾科夫決策過程求解,以獲得累計獎勵最大的系列動作,即最優減載策略,實現多微網非計劃孤島切換。基于IEEE-33節點的仿真算例驗證了本文所提策略相較于加速減載策略能夠更快、更加經濟地實現多微網非計劃孤島切換。

1 多微網非計劃孤島

1.1 非計劃孤島概述

多微網非計劃孤島是指當大電網發生故障,供電質量無法得到保證時,多微網為保證自身安全,斷開與大電網間聯絡線轉為孤島運行的過程。在非計劃孤島過程中由于聯絡線的斷開,多微網內部分布式電源無法彌補聯絡線功率轉移而存在較大的功率缺額。若不及時處理,會對微電網穩定運行帶來威脅,嚴重時將導致多微網的電壓和頻率崩潰。

目前,低頻減載是從工程實際應用角度出發解決多微網非計劃孤島平滑過渡的有效方法之一。當多微網調節自身儲能出力仍不能解決供需問題時,可通過低頻減載技術切除多微網內部的非重要負荷,迅速彌補多微網孤島切換過程中的功率供需不平衡。

1.2 低頻減載建模

1.2.1 功率缺額

在多微網非計劃孤島過程中,系統內部的功率缺額可利用系統廣域測量得到的頻率變化率來估算。估算公式為

(1)

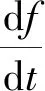
1.2.2 負荷特性

由于負荷特性的差異,切除不同負荷會帶來不同的頻率調節效果。對于某一特定負荷,其切除時多微網系統的頻率變化量與切負荷量之間滿足如下關系。

Δf=KLΔPLS

(2)

式中:KL為特定負荷的頻率調節效應系數;ΔPLS為負荷的減載量;Δf為執行減載動作后多微網系統頻率較動作前的變化量。

1.2.3 減載成本

在多微網孤島切換過程中,除考慮減載量外,還應注意到減載的經濟性問題。多微網孤島切換的減載過程應在使系統迅速恢復穩定運行的前提下,最小化減載損失。減載損失模型如下。

(3)

式中:W為總的減載經濟損失;n和m分別為多微網內子微網的個數和子微網內的負荷個數;Kg,i、Pshed,g,i分別為第g個子微網內第i個負荷的減載損失系數和減載量。

2 基于DQN算法的多微網非計劃孤島切換策略

2.1 DQN算法

Q-learning算法是基于馬爾科夫決策過程框架提出的無模型學習方法[11]。一般而言,馬爾科夫決策過程可由元組(S,A,P,R)來定義。狀態空間S和動作空間A都是離散變量;環境轉移函數P是指由當前狀態st∈S向下一狀態st+1∈S轉移的概率。在每一次迭代中環境會根據智能體的動作at∈A反饋一個獎勵值rt∈R,智能體再根據環境反饋的獎勵采取下一個動作。如此反復,智能體將會學習到1個累計獎勵最大的策略πθ=(st,at)。智能體與環境之間交互的框架見圖1。

圖1 智能體與環境交互基本結構

作為深度學習與Q-learning算法的結合,DQN算法很好地繼承了深度學習提取高維特征和非線性擬合的強大性能,能夠利用神經網絡準確評估不同狀態-動作組合下的Q值。為減小數據在時間上的關聯度,DQN算法還引入經驗回放機制和雙網絡結構。經驗回放是指DQN算法在訓練過程中將訓練后的樣本數據存入至經驗池內,在后續訓練時可隨機從經驗池中采樣小批量歷史樣本數據進行網絡參數的更新。雙網絡結構是指構建結構相同的評估網絡Qeva和目標網絡Qtar,評估網絡用來評估當前狀態下每一個動作的Q值。經過一定回合的訓練后,評估網絡的參數會被傳輸賦值給目標網絡。

2.2 馬爾科夫決策過程建模

馬爾科夫決策過程可由元組(S,A,P,R)來定義。

a.狀態空間(state):多微網發生非計劃孤島瞬間,多微網無法彌補聯絡線功率缺額時,需通過減載使多微網系統恢復穩定。選取狀態空間如下。

(4)

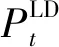
b.動作空間(action):由于主要研究對象是多微網非計劃孤島后如何通過減載解決功率缺額的問題,選取動作空間如下。

(5)

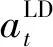
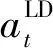
(6)

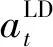
d.狀態轉移(state transition)：采取減載動作后，多微網內部功率缺額和負荷實時功率一定會發生變化。因此，多微網系統的狀態轉換具有確定性。

2.3 優先經驗回放機制

為減小訓練數據在時間上的關聯度，DQN算法引入優先經驗回放機制。優先經驗回放可以提高時序差分誤差較大樣本數據的重采樣概率。在經驗池中，樣本i的采樣概率為

(7)

式中:τ為調節經驗樣本重要性的系數;k為求和序列的上界;pi為第i個經驗樣本的優先級。

基于等級的優先級表示為

(8)

式中:rank(i)表示回放內存排序時轉換i的秩。

2.4 基于DQN的減載策略學習過程

在DQN算法的訓練過程中，智能體會不斷與多微網環境間進行交互調整，以期望獎勵最大化。智能體每一回合的訓練都是一個學習的過程，Q網絡參數會隨著學習的進行不斷得到修正。DQN算法在訓練過程中，評估網絡Q值更新滿足式(9)。

(9)

使用均方差作為DQN算法的損失函數,損失函數可定義為

(10)

式中:θeva是評估網絡的特有參數。

利用隨機梯度下降法來最小化該損失,即可得到最優的減載策略。執行該減載策略即可實現多微網非計劃孤島的無縫切換。圖2為基于DQN算法的多微網非計劃孤島切換的流程。

圖2 非計劃孤島切換流程

3 算例驗證

3.1 多微網信息數據

為驗證提出多微網非計劃孤島切換策略的有效性,在MATLAB軟件中搭建如圖3所示的改進IEEE-33節點仿真系統模型。該多微網模型由3個子微網組成,包含7個儲能裝置,9個光伏板和9個負荷。選取MG-1中的BES1、MG-2中的BES2、MG-3中的BES5作為多微網系統主儲能,在多微網孤島運行時采用VF運行模式,其他儲能及光伏采用PQ控制。模型中9個負荷數據信息如表1所示,多微網源荷儲配置信息如表2所示。

表1 多微網負荷數據信息

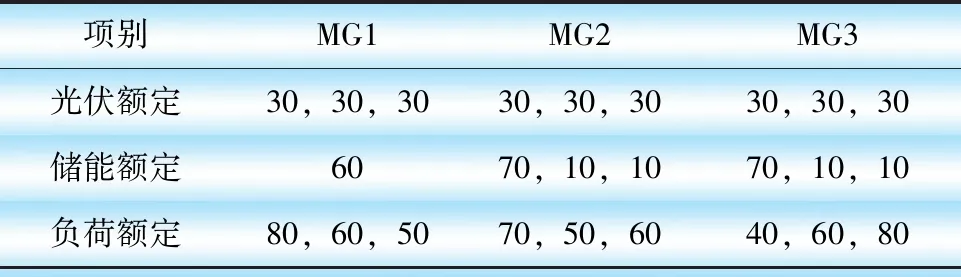
表2 多微網配置信息 單位:kW

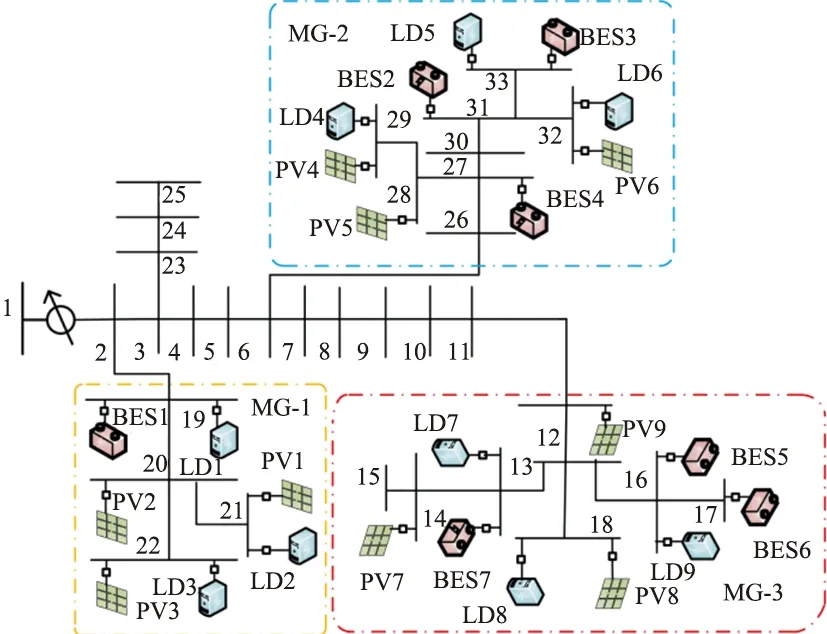
圖3 改進IEEE-33節點系統模型

3.2 DQN算法訓練

在利用DQN算法進行多微網非計劃孤島減載過程前,需要對DQN算法進行訓練。圖4為DQN算法的收斂曲線。由圖4可知,在經過約900個訓練回合后,DQN算法實現穩定收斂。此時,DQN算法已對多微網環境進行了充分探索,學習到了最優的減載策略。

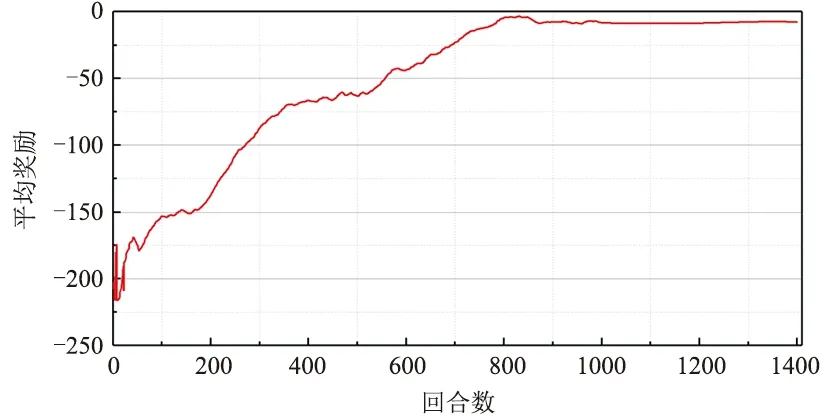
圖4 DQN算法獎勵收斂圖

3.3 基于改進IEEE-33節點的多微網非計劃孤島測試

多微網在t=1.2 s時進入孤島運行,此時多微網需承擔原聯絡線轉移功率為260 kW。在調節分布式電源出力后,仍不能滿足多微網內功率平衡,需進行切負荷操作。通過多微網廣域系統測量,并依據式(1)估算得功率缺額為183 kW。將本文所提策略與文獻[9]所提加速減載策略對比,執行減載策略后各負荷節點的切負荷情況如圖5所示。圖6為執行減載策略后,多微網系統的頻率恢復曲線。

圖5 負荷節點切負荷情況

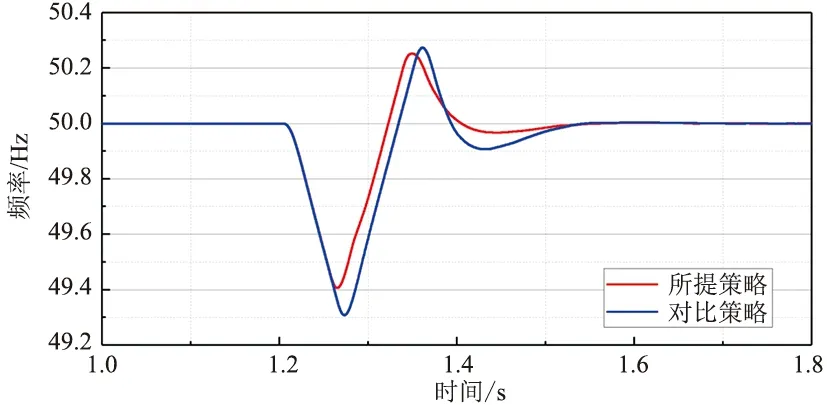
圖6 頻率恢復曲線

由圖4可知,所提策略在考慮負荷重要性的前提下對負荷LD1、LD2、LD4、LD6、LD9進行部分減載,所提策略避免了重要負荷的供電中斷。經由式(3)計算可得出減載損失為6200元。對比策略在減載時,利用頻率變化率加速減載,并未考慮負荷切除的優先級,造成了重要負荷LD3、LD5、LD7、LD8的切除,減載損失為12 030元,比所提策略減載損失高出5830元。

由圖5可知,所提策略在頻率恢復周期內的波動范圍為49.42～50.25 Hz,在多微網非計劃孤島發生后經過0.3275 s使頻率恢復至正常穩定運行狀態。對比策略頻率波動幅度較所提策略高0.14 Hz,且頻率恢復周期較長,比所提策略慢0.107 s。

綜上所述,所提策略能通過多微網自身調節及低頻減載的共同作用,消除多微網非計劃孤島過程中的功率缺額。與文獻[9]的策略相比,本文所提策略能夠在更短時間內使多微網頻率恢復至正常穩定運行狀態,且頻率波動幅度更小。同時,所提策略避免了微網內重要負荷的切除,保證了微網內重要負荷的可靠供電,減載造成的經濟損失更小。

4 結語

針對多微網非計劃孤島切換過程中由于聯絡線斷開導致多微網內部產生大量功率缺額的問題,提出一種基于DQN算法的多微網非計劃切換策略。策略利用DQN算法學習到的最佳減載策略,實現了多微網非計劃孤島的平滑過渡。算例仿真結果驗證了所提多微網非計劃孤島切換策略的可行性和有效性。