飛機和風機葉片除冰用脈沖線圈結構對瞬態電磁場影響研究

陳 宇 蔣興良 黃廷帆,2 姜 濤 胡 琴

飛機和風機葉片除冰用脈沖線圈結構對瞬態電磁場影響研究

陳 宇1蔣興良1黃廷帆1,2姜 濤1胡 琴1

（1. 重慶大學雪峰山能源裝備安全國家野外科學觀測研究站 重慶 400044 2. 陸軍工程大學通信士官學校 重慶 400044）

在飛機和風機葉片電脈沖除冰中，為了提高線圈的脈沖效果，降低除冰裝置質量，實現系統的微功耗設計，需要優化線圈結構。脈沖線圈作為脈沖除冰、脈沖焊接等應用中能源轉換的關鍵部件，其瞬態電磁場求解復雜，一般難以得到解析解。為了研究線圈結構參數對脈沖效果的影響，該文通過推導脈沖線圈的場-路數學方程，建立脈沖線圈和目標物的物理模型，并采用有限元軟件對脈沖線圈的瞬態電磁場進行計算，得到脈沖線圈電磁參數時變特性。通過脈沖線圈的脈沖沖量試驗對模型的準確性進行驗證，在此基礎上，分析線圈匝數、截面尺寸和線圈匝間距等結構參數對脈沖電流、脈沖力、脈沖效果的影響，為電脈沖除冰應用微功耗化設計提供優化思路和技術路線。

脈沖線圈 瞬態電磁場 脈沖效果 結構參數

0 引言

相比常見的電熱融冰法，電脈沖除冰是一種功耗小、速度快的除冰方式[1-2]，其中能量轉換部件為脈沖線圈。脈沖線圈在脈沖焊接[3-4]、無損探傷[5-7]、新型直流斷路器[8]和無線傳輸[9]等領域也有應用，其作為電能轉換為機械能或電能的關鍵部件不可或缺。在不同領域中，由于實現的目標不同，脈沖線圈的結構、電磁參數、布置和使用方式差別很大。在脈沖焊接和新型直流斷路器的試驗測試中，脈沖線圈將瞬時的電能通過磁場轉化為目標物中的機械能，使目標物產生塑性形變或位移。

國內外針對脈沖線圈的不同應用領域研究各有側重點。脈沖焊接主要關注目標物的塑性形變和不同異形金屬件的焊接效果；新型直流斷路器更關注目標物的受力過程；而在電脈沖除冰中，研究人員則將重點集中在目標物的電動力學、結構動力學和除冰效果等方面，但由于電磁場瞬態計算較為復雜，大部分的瞬態問題暫時無法得到精準的時域解析解[10]。目前，俄羅斯已升級至第四代電脈沖除冰系統，采用新材料和新結構，其質量比第三代系統更輕，并進一步提升了系統可靠性，使其除冰環境溫度降低至-50℃。由于我國的飛機對除冰的需求比俄羅斯低，在國內還未廣泛應用微功耗、輕量化的電脈沖除冰系統[11]。隨著計算機的發展，數值計算在電磁場的應用越來越多[12]，但對電脈沖除冰情景下的瞬態電磁場研究較少。特別是在不同電路參數下，脈沖線圈的電磁場變化及脈沖效果都缺乏相應的研究。

在20世紀，蘇聯、美國先后在飛機機翼電脈沖除冰方面開展研究，蘇聯已經成功地將其應用在伊爾系列飛機上，美國也已將其實現商業化[13]。目前我國主要在美國威奇塔州立大學（Wichita State University, WSU）飛機機翼電脈沖除冰方法的研究基礎上開展相關探究。

美國R. A. Henderson博士利用M. H. S. Ei-Markabi和F. M. Freeman提出的電磁場建模技術，建立一種計算脈沖線圈的電磁場傳輸線模型，該模型初步計算線圈的放電電流、鋁板所受的脈沖力，但它是一種通過頻域近似計算的方法[14]。R. L. Schrag和W. D. Bernhart等提出了關于脈沖線圈的電磁場Bernhart-Schrag模型，通過將線圈和目標物同時劃分為矩形單元，并建立單元間的電感矩陣，求得目標物的電磁力，但未對脈沖線圈結構參數進行分析[15]。南京航空航天大學李清英等認為，在電頻率一定時，脈沖電流峰值最大則脈沖效果最好，并以此提出了線圈的設計方法[13]。E. Moehle等對鋁板上的電脈沖力進行電磁場和結構動力學耦合分析，并進行除冰試驗，驗證仿真的有效性[16]，但同樣未對線圈進行優化分析。郭濤在此基礎上建立了電脈沖除冰的有限元分析模型，為了降低計算難度，使用空心圓柱體來等效脈沖線圈[17]，但在數值計算中，程序無法區別線圈截面和尺寸信息，對脈沖線圈的電氣參數計算不準確，難以說明線圈的尺寸參數和匝數對計算結果的影響。重慶大學王洋洋等提出一種針對瞬態電磁場計算的有限元耦合方法，對導體域采用邊光滑有限元法（Edge Smooth-Finite Element Method, ES-FEM），對非導體域采用邊界元法（Boundary-Elements Method, BEM），能夠提高求解速度和精度，但未將該方法應用于脈沖線圈的瞬態電磁場計算中[18]。同時重慶大學黃廷帆等在試驗研究中發現[19]，隨著脈沖線圈匝數的增加，線圈電阻和電感同時增大，獲得的總脈沖沖量呈上升趨勢。相對于不變的電容和能量條件下，脈沖電路中的電流峰值會下降，出現峰值電流的時間滯后，進而使脈沖力峰值降低。在試驗中需要控制的變量太多，且單個線圈在多次試驗后，局部過高的溫度會影響線圈電阻，進而影響試驗結果。此外，在電脈沖除冰的研究中，普遍使用平面式螺旋線圈，線圈截面主要為矩形，僅部分研究使用了圓形截面的線圈。

綜上所述，已有學者對脈沖線圈及目標物進行電磁場、電磁力計算和數值計算方法的研究，但均未對其結構參數的影響進行深入探索。本文從電路和電磁場的基本原理出發，建立矩形截面的脈沖線圈和目標物物理模型，確定電路參數、瞬態電磁場的控制方程及邊界條件，通過數值方法計算不同線圈下的電氣參數和瞬態電磁場，具體分析線圈尺寸、線圈匝數、線圈內外徑結構參數對脈沖電流、脈沖力和脈沖沖量的影響，得到固定電路參數下，較優的脈沖線圈結構參數，對電脈沖除冰應用微功耗的優化設計具有一定的指導。

1 脈沖線圈的場-路物理數學方程

1.1 脈沖線圈的放電電路

脈沖線圈放電過程是一種RLC的欠阻尼二階電路，其電路如圖1所示。其中，為充、放電電容，作為放電電路的電源；VD為鉗位二極管，用來保護電容；d為鉗位二極管自帶電阻；SCR為晶閘管，當電容充電完成準備除冰時，可通過控制電路控制其閉合；l和l分別為線路的電阻和電感，其值基本不變；c和c分別為線圈的電感和電阻；O為目標物，通常為鋁板。

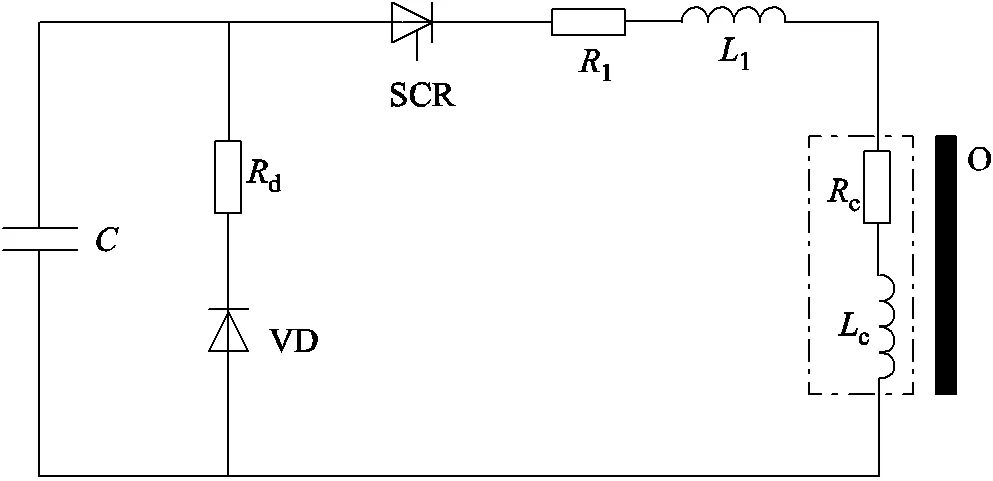
圖1 脈沖線圈放電電路

對于圖1所示電路，可以得到其二階電路中的電流方程為

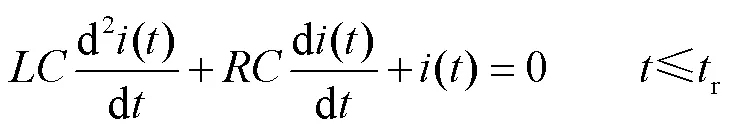
式中，()為脈沖電路電流（A）；為電路電感（H），由線路電感和線圈電感組成；為放電電容（F）；為電路電阻（Ω），由線路電阻和線圈電阻組成；r為電容反向充電時刻（s）。由于鉗位二極管的作用，線圈不會對電容反向充電。

在本文中，反向電流只會通過鉗位二極管自行耗盡，且主要研究0～r內的過程。線路參數和電容參數在瞬態計算中基本無明顯變化，但在目標物渦流的影響下，線圈電阻、電感變化很大，這將給場-路耦合帶來困難。

由式（1）可進一步得到脈沖電流為

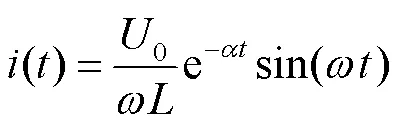
其中

式中，0為電容初始放電電壓（V）；為振蕩電路的衰減系數；為衰減角頻率。

1.2 脈沖線圈的電磁場

為了求解脈沖線圈的瞬態電磁場，本文從麥克斯韋方程出發，將目標域分解為感應域（目標物）、源域（線圈）和空氣域三個部分，如圖2所示。采用矢量磁位和標量電位來表示場域的控制方程及其邊界條件。式（3）和式（4）分別為位函數、的定義，并采用庫倫規范。

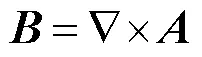
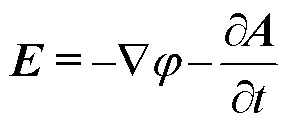
式中，為求解域的磁感應強度（T）；為求解域的電場強度（V/m）。

圖2 待求解的目標域

對于源域和空氣域，有

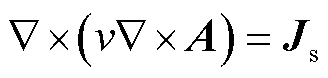
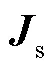
對于感應域（目標物），有

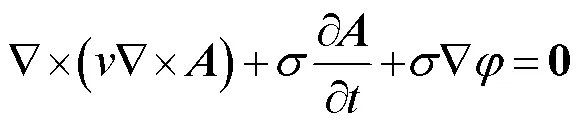
求解域的邊界條件分別為

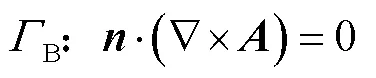
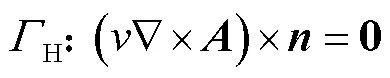
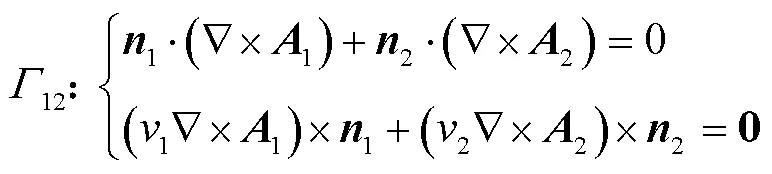
式中，、1、2分別為空氣域、源域和感應域邊界相應表面的外法向分量；1、2分別為源域和感應域的磁阻率；1、2分別為源域和感應域的矢量磁位；B和H是空氣域與外部相連的兩種不同邊界，并分別規定邊界的磁感應強度的法向分量和磁場強度的切向分量為零；12為感應域和非感應域的邊界。

1.3 場-路耦合

在脈沖線圈的計算中，通過位函數、作為中間變量進行耦合。由法拉第定律可以得到線圈電壓方程為

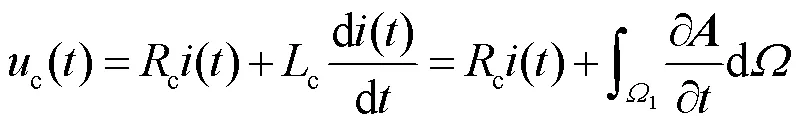
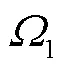
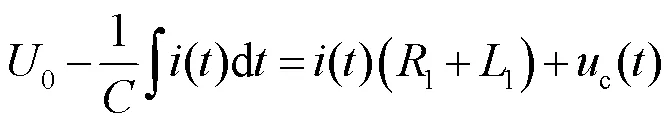
聯立式（10）和式（11），即可實現場-路耦合。

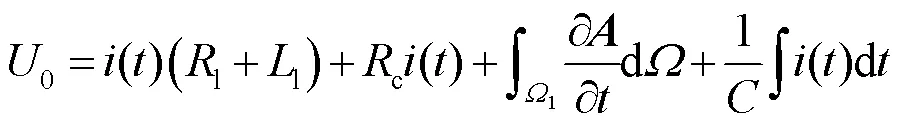
1.4 目標物的脈沖力及沖量

1.4.1 目標物的脈沖力密度分布

通過式（3）、式（4）、式（13）計算得到瞬態磁場磁感應強度和目標物內的感應渦流e，利用電磁力公式可以獲得目標物的脈沖力密度分布，進而可以得到脈沖力分布。

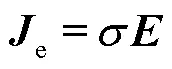
式中，e為目標物內渦流密度（A/m2）。

本文所采用的數值計算模型如圖3所示。由圖3及電磁原理可得，目標物中的渦流主要垂直穿入/穿出在平面。根據左手定理，目標物所受電磁脈沖力主要為軸方向上，故在本文中主要研究脈沖力的軸分量，可得

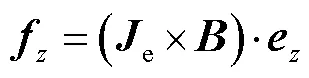
式中，fz為目標物在z軸方向所受脈沖力密度（N/m2）；為z方向上的單位向量。

1.4.2 目標物的脈沖合力及沖量

將目標物上所有單元所受脈沖力進行體積分，可以得到目標物所受脈沖合力。根據分析可知，目標物所受軸方向脈沖力較小，同時，目標物在除冰時主要依靠軸方向的脈沖力，故本文重點分析在軸方向的分量。

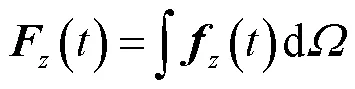
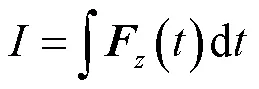
式中，()為目標物在軸方向所受脈沖力（N）；為目標物在軸方向所獲得的沖量（N·s）。

將目標物所受脈沖合力對時間求積分可以得到目標物在一次脈沖作用下獲得的沖量，如式（16）所示，脈沖沖量可以進一步表征脈沖力的作用效果。根據除冰試驗，可以發現除冰效果與脈沖沖量呈正相關。

2 瞬態電磁場模型及結果

2.1 脈沖線圈的計算模型

有限元仿真需要對電脈沖線圈和目標物進行物理建模，若對實際脈沖線圈進行有限元計算會十分復雜，為了更好地研究其線圈形狀參數與脈沖效果的關系，由于脈沖電路頻率低于10 kHz，故需要作以下假設：①忽略位移電流對電磁場的影響；②忽略在電容器放電期間的目標物的外界受力及運動情況；③將模型簡化為二維軸對稱（）模型，同時將螺旋線圈近似用同心圓線圈替代，計算模型如圖3所示，以鋁板下表面為=0 mm。

2.2 模型設置與求解工況

模型中，源域材料為銅（電導率為5.8×107S/m，相對磁導率為0.999 991），目標物材料為鋁（電導率為3.48×107S/m，相對磁導率為1.000 021），本文主要研究線圈結構參數，故并未對材料進行深入探究。除3.3節中所提到鋁板與引用文獻的測試情況一致外，本文所研究的目標物直徑為100 mm、高為4 mm，線圈與目標物間隙為3 mm，空氣域尺寸為300 mm×300 mm×100 mm。

由于脈沖電流將在目標物中感應出渦流，故需要對目標物網格進行趨膚深度距離內的細化。將頻率設定為1 kHz，通過目標物材料的磁導率和電導率，根據式（17）可得其趨膚深度，由此將該范圍內的網格進一步細化。

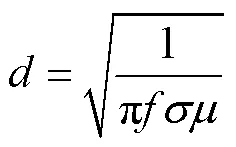
本文中40匝線圈模型的單元參數見表1，其中單元大小和單元數量均為各個工況下的最大結果。針對二維電磁場-路耦合計算，為減少計算總時長，加快電路電流衰減速度，將d值設置較大，故模型時間設置見表2，并保存每個時間步。

表1 40匝線圈模型的單元參數

Tab.1 The unit parameters of the 40-turning coil model

表2 模型瞬態時間參數

Tab.2 Model transient time parameters

2.3 脈沖線圈的瞬態電磁場

2.3.1 脈沖線圈的電氣參數

在研究脈沖線圈渦流場的過程中發現，有無目標物對脈沖線圈的電磁參數有很大影響。無目標物時，脈沖線圈電阻、電感基本不隨頻率的變化而變化；有目標物時，其電阻、電感都將隨源域的頻率改變而發生變化。

匝數為40、100的線圈在有目標物條件下的電阻、電感曲線如圖4所示?？梢钥闯?，在有目標物時，線圈電阻隨頻率的增大而增大，線圈電感隨頻率的增大而減小。對于大匝數的線圈而言，在頻率低于1 kHz以下時，電阻變化較緩，而在1～10 kHz時，電阻將快速增大；相反，電感的變化呈現先快后緩的趨勢。脈沖除冰中，其瞬時頻率不會較大，其峰值也在數百微秒，故取1 kHz為作為趨膚深度頻率。

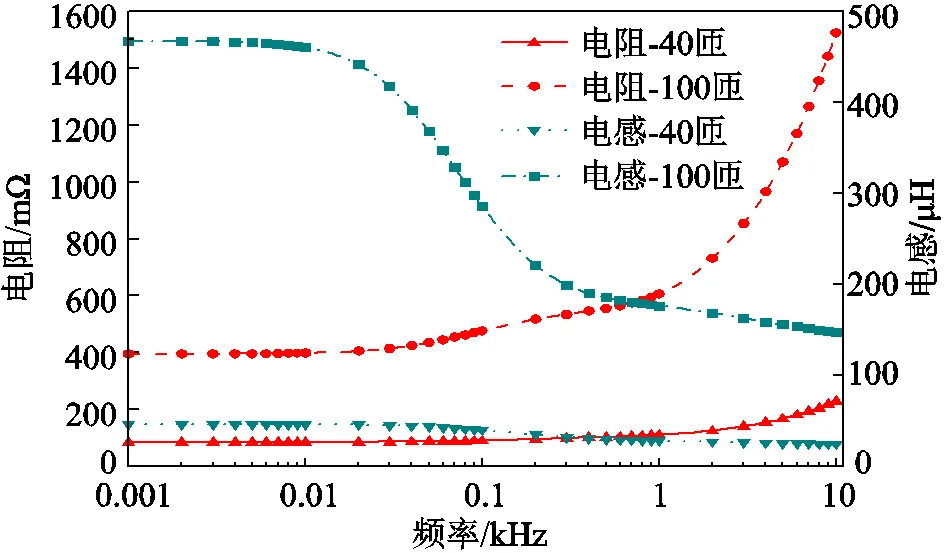
圖4 線圈電阻、電感隨頻率的變化

相同內徑、相同線圈截面、相同匝間距的不同匝數線圈電阻、電感的計算結果見表3。隨著線圈匝數的增大，線圈的外徑也將變大，在相同目標物的條件下，線圈的電阻、電感較無目標物時變化更大，這將影響線圈的脈沖效果。

表3 有、無目標物條件下的線圈電阻、電感

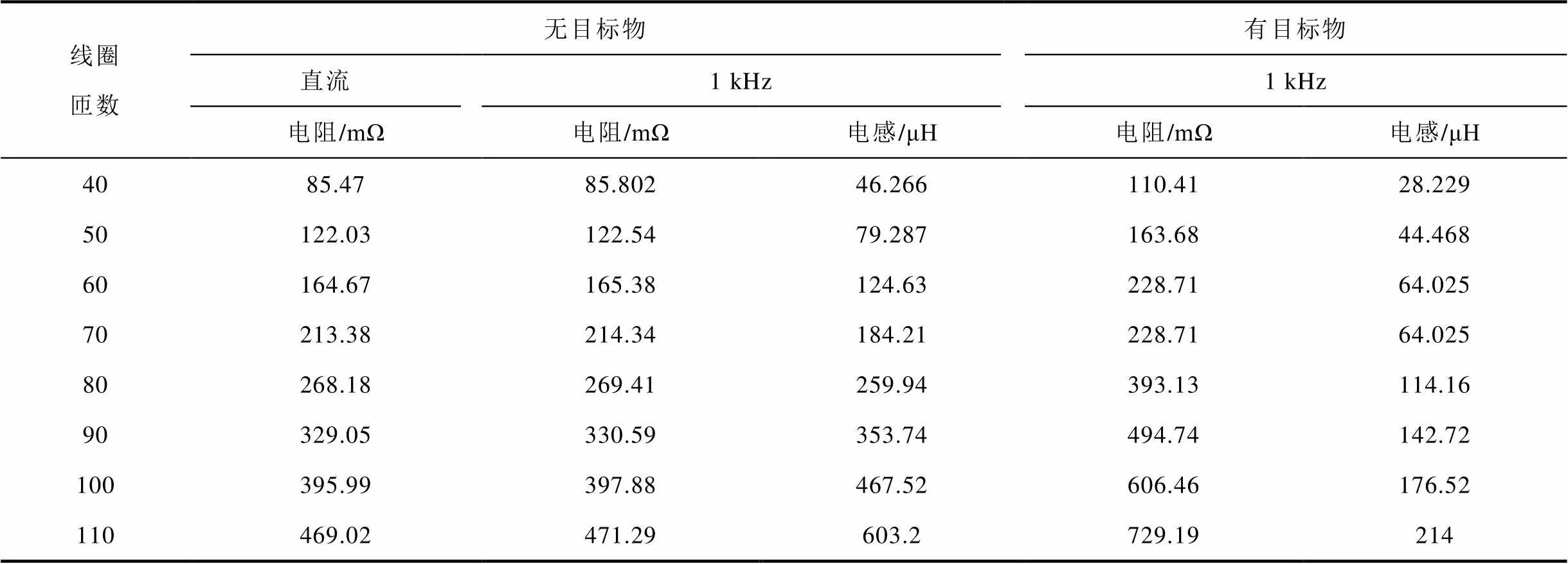
Tab.3 Resistance and inductance with and without target

2.3.2 脈沖線圈的瞬態磁場

在目標物不變的情況下，脈沖線圈的瞬態磁場分布主要由脈沖線圈參數和脈沖電路共同作用，即脈沖電流的分布。

內徑為14 mm的40匝線圈在目標物上產生的磁感應強度分布如圖5所示。圖6是不同位置點上，目標物沿軸向和徑向的磁感應強度分布。由圖5可知，當脈沖合力最大時，在目標物上出現最大的磁感應強度=2.682 7 T。

由圖5、圖6可知，當=95 μs時，對于=0 mm這條線，磁感應強度的徑向分量B在=0～16 mm之間單調遞增，在=16～100 mm之間單調遞減，在=16 mm、=0 mm處出現極大值2.720 T；磁感應強度縱向分量B分別在=8 mm、=24 mm上出現極值，但該值較小，即鋁板在軸方向所受脈沖力較小，故后文并不對B和脈沖力的向分量（F）進行研究。對于=16 mm這條線，B在=1～4 mm之間單調遞減，即目標物距線圈越遠的區域感應脈沖力越小。

圖6 目標物上磁感應強度分布

2.3.3 目標物的感應渦流

進一步地，可以得到目標物內渦流密度的分布，如圖7、圖8所示?？梢钥闯觯谌鐖D3所示的模型中，電流和渦流密度都只垂直穿入/穿出于圖3中的線圈截面。

圖7為不同時刻下目標物渦流密度場分布，可以看出渦流密度主要集中在靠近線圈的區域內，隨著目標物的其他區域與源域距離增大，渦流密度呈指數式下降，最大值和最小值之間相差大約1 000倍。

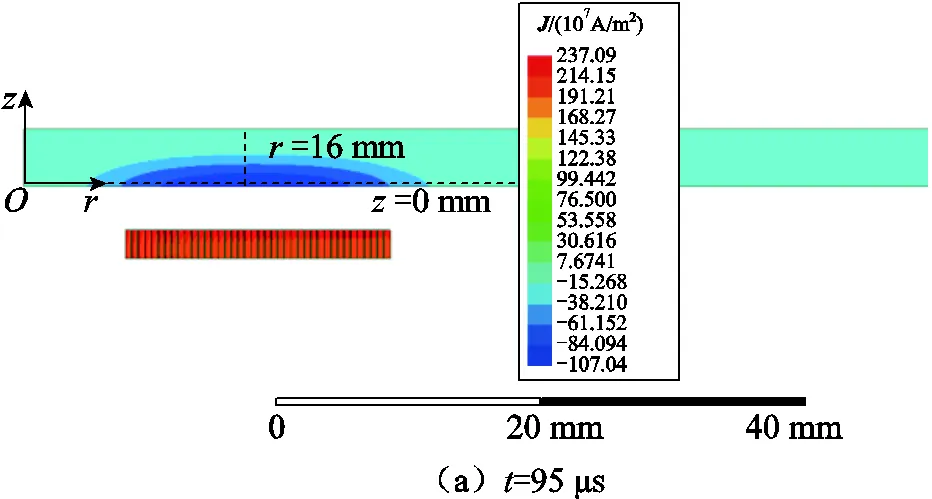
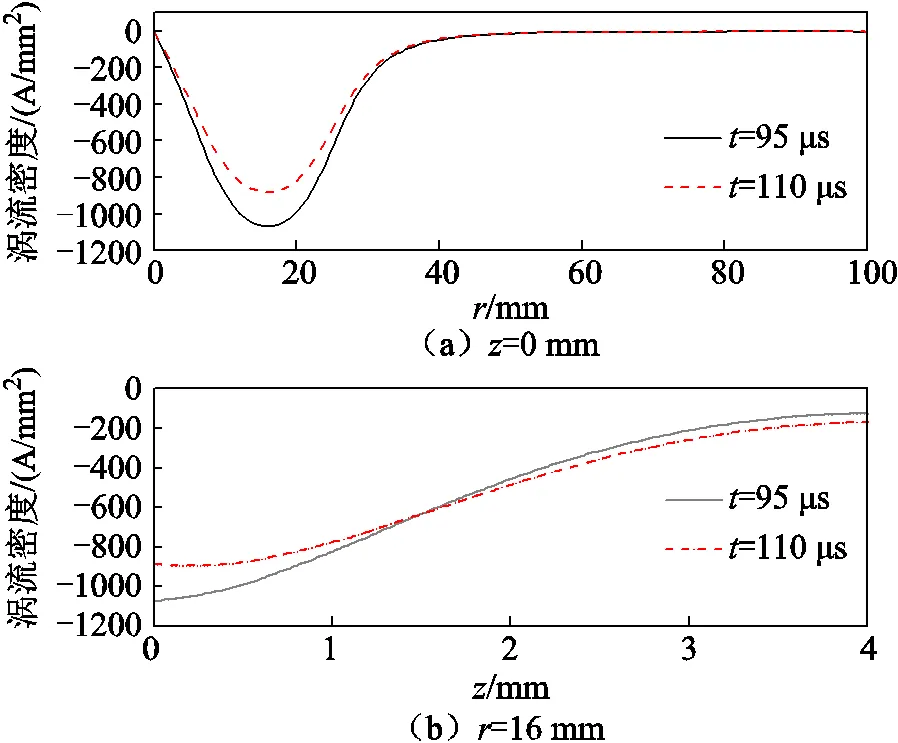
圖8 目標物內渦流密度隨位置變化

圖8為目標物不同位置的渦流密度分布沿軸向和徑向的變化，可以得到，在脈沖力最大時，渦流密度最大，而在脈沖電流最大時，渦流密度下降，表明渦流和脈沖合力峰值時間超前于脈沖電流峰值。由圖8a可以看出，渦流主要集中在線圈內、外徑對應的區域；由圖8b可發現，隨著高度的增加，目標物渦流密度逐漸降低。

2.3.4 目標物的脈沖力及沖量

根據目標物的渦流密度和磁感應強度，可以得到不同位置上的脈沖力分布。由于模型被劃分為許多三角形單元，通過平均值來表征該區域內的脈沖力密度分布。不同時刻目標物的脈沖力密度分布如圖9所示。圖9a是目標物最底面的脈沖力分布，可見脈沖力在=0 mm=4～32 mm以外的區域都近似為零，表明目標物能夠產生脈沖力的區域面積同線圈面積近似；圖9b是目標物沿=16 mm處的脈沖力分布，當＞2.5 mm后，磁感應強度和渦流密度都比較小，脈沖力基本接近于零。

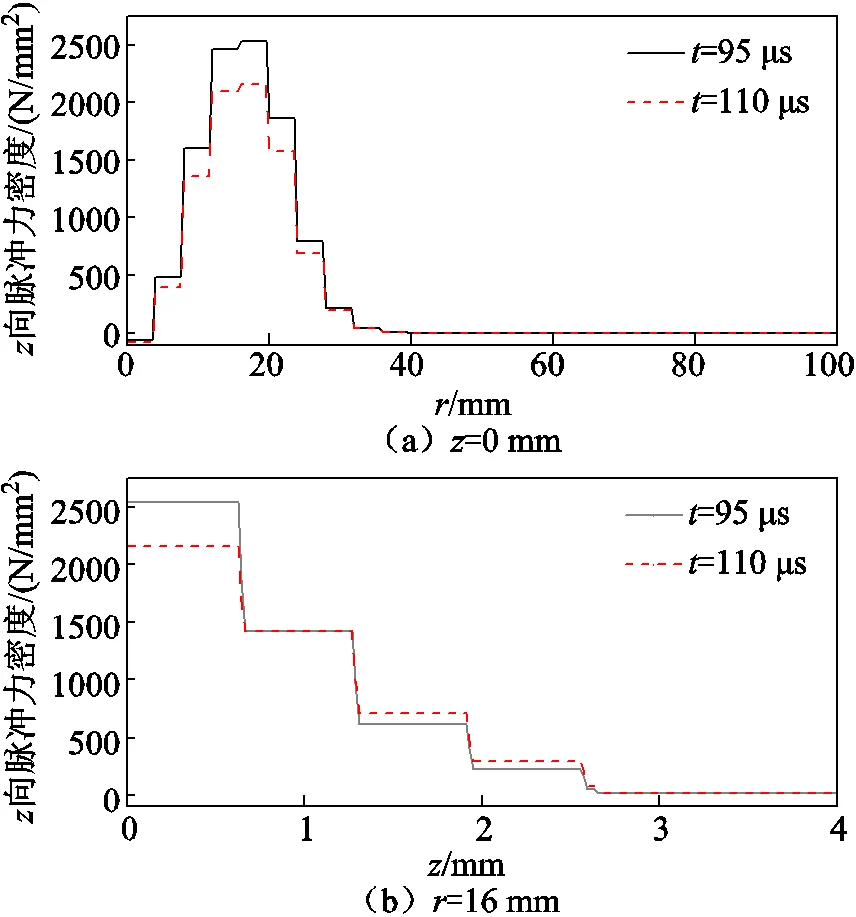
圖9 目標物的脈沖力密度分布

進一步地，通過對脈沖力依次進行空間、時間上的積分，最終得到40匝線圈下的目標物受到的沖量為0.742 8 N·s。

2.4 計算值和測量值對比

本文對40、50、60匝線圈進行加工，得到如圖10所示的脈沖線圈，測量其不同條件下的電阻、電感，并同2.3.1節中的進行比較，其結果見表4。需要說明的是，為簡化計算，未對線圈的進、出線進行建模，表3中的電阻總體較測量值小15～25 mΩ，該部分電阻在計算中并入1。

圖10 脈沖線圈實物

表4 線圈電感、電阻的測量值

Tab.4 Measurement of coil inductance and resistance

同時，利用文獻[20]中所采用的擺錘法，實時測量上述三種線圈的脈沖效果，并同計算得到的結果進行比較，結果見表5。

表5 脈沖沖量的計算值和測量值比較

Tab.5 Comparison of calculated and measured impulses

總體來說，仿真結果與測量結果相差較小，最大誤差為14.2%。導致誤差的主要原因有：①測量過程中存在各方面的誤差，如擺錘自身運動過程中的消耗、測量精度的誤差；②數值計算模型較為理想，目標物和線圈一直保持相同距離，而實際中，目標物將作為非固定物體進行運動，故實測值總體小于計算值。綜上所述，數值計算與測量結果相近，具有較高的可信度。

3 線圈結構參數對脈沖效果的影響

脈沖線圈結構參數的變化，將導致脈沖線圈的電磁參數變化，在相同目標物和相同放電電路條件下，線圈電流分布的變化會導致求解空間磁場的變化，最終將改變脈沖線圈的脈沖效果。而脈沖電流峰值時刻，脈沖合力并未達到最大值，在本節中，主要對脈沖合力峰值時刻展開討論。

如圖10所示，實際線圈屬于緊密繞制，故線圈的匝間距僅為加上兩端漆層的扁線厚度。在本節中，電容參數保持不變，均為=400 μF、0=DC 1 200 V，通過測量得到線路阻抗和各個接觸電阻為l=0.275 Ω、l=1 μH、d=10 Ω。

3.1 線圈匝數

固定線圈內徑、截面尺寸、匝間距，改變線圈匝數，得到不同線圈匝數的脈沖合力的峰值和峰值時間、脈沖沖量見表6。圖11為不同匝數脈沖力峰值時刻，=0 mm上脈沖力密度沿軸的變化。

表6 不同線圈匝數的脈沖效果

Tab.6 Impulse effect of different coil turns

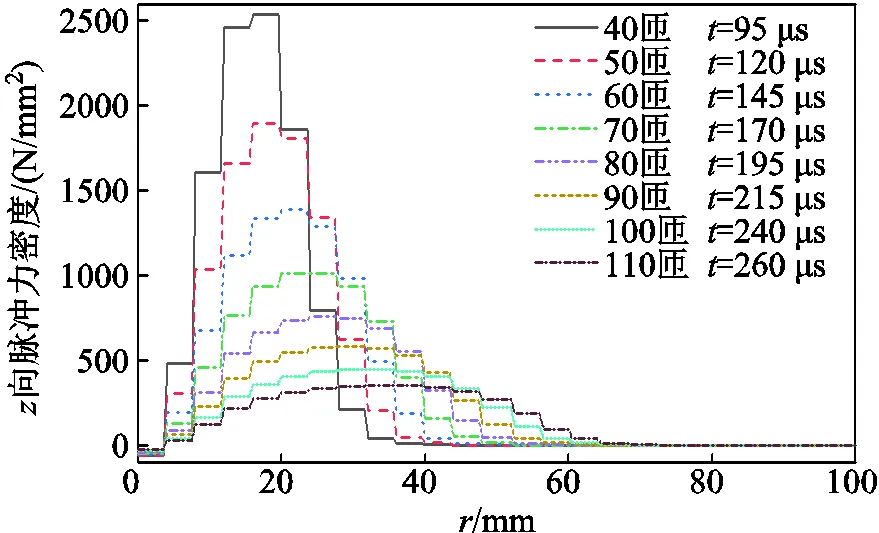
圖11 不同匝數脈沖力密度隨距離的變化

隨著匝數的增大，其電阻、電感將增大，而在其他計算參數不變的條件下，脈沖合力峰值先增大后減小，峰值時間隨著電阻、電感的增大而增大。匝數的增大使得脈沖電流下降，降低向脈沖力的峰值；同時也增大脈沖電流作用的面積，使得目標物上更大面積的磁感應強度發生變化，從而產生渦流，形成脈沖力，因此線圈脈沖沖量會隨匝數的增大而持續增大。

但線圈外徑逐漸增大時，導致線圈阻抗增大，脈沖頻率下降，無法實現在高應變率下的除冰。尤其是當線圈外徑超過目標物的外徑后，其除冰效果將大幅下降。

3.2 線圈截面尺寸

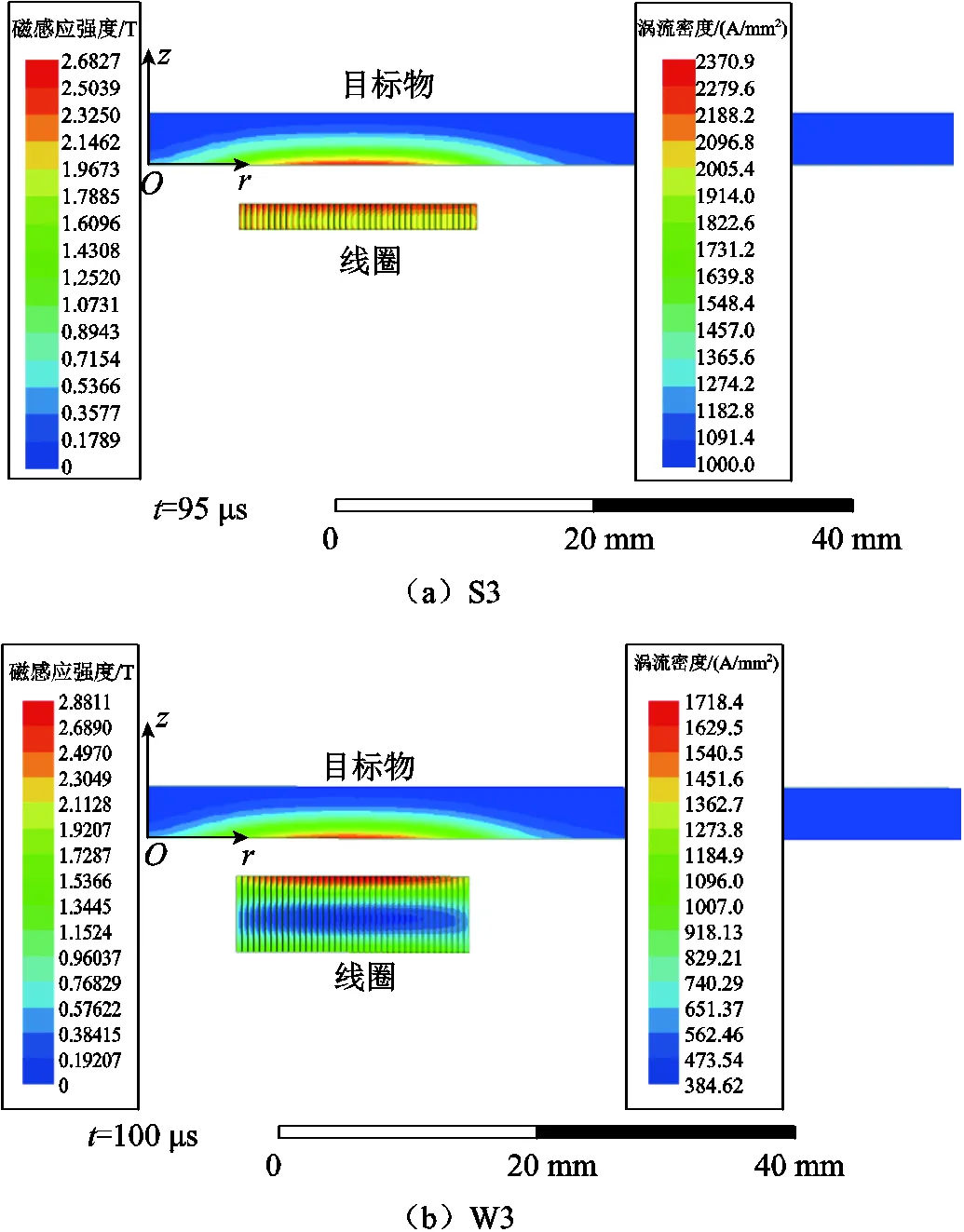
固定線圈內徑、匝間距、匝數，改變線圈截面尺寸。脈沖線圈觸發時需瞬間通過數kA電流，為了裝置可靠性和耐久度，其截面不能太小。同時，受制作工藝和線圈加工繞制的制約，本文選取線圈截面為0.2 mm×4 mm（寬×高，下同）、0.3 mm×2.67 mm、0.4 mm×2 mm三種保持相同截面積的尺寸（分別記為S1～S3），和0.4 mm×2 mm、0.4 mm×3 mm、0.4 mm×4 mm、0.4 mm×6 mm、0.4 mm×8 mm、0.4 mm×10 mm六種保持相同寬度的尺寸（分別記為S3、W1～W5）來探究其截面尺寸的影響，計算結果如圖12所示和見表7。

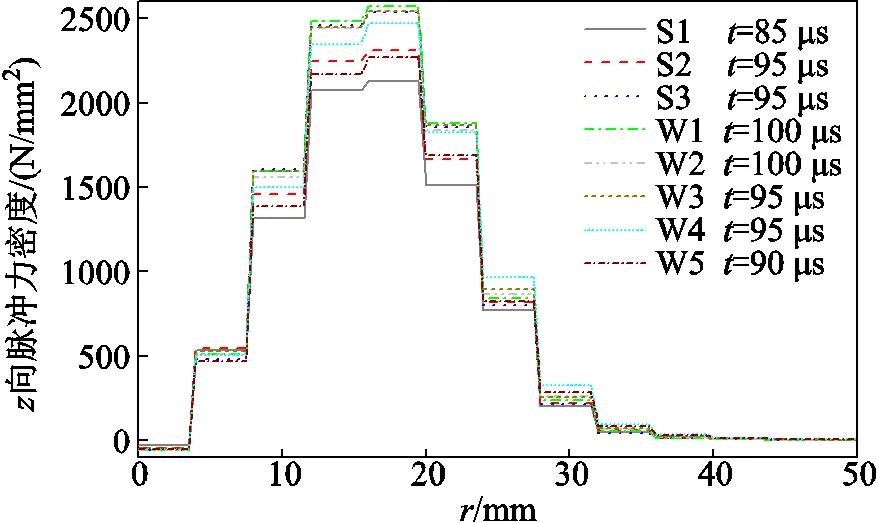
圖12 不同截面尺寸脈沖力密度隨距離的變化

表7 不同截面尺寸線圈的脈沖效果

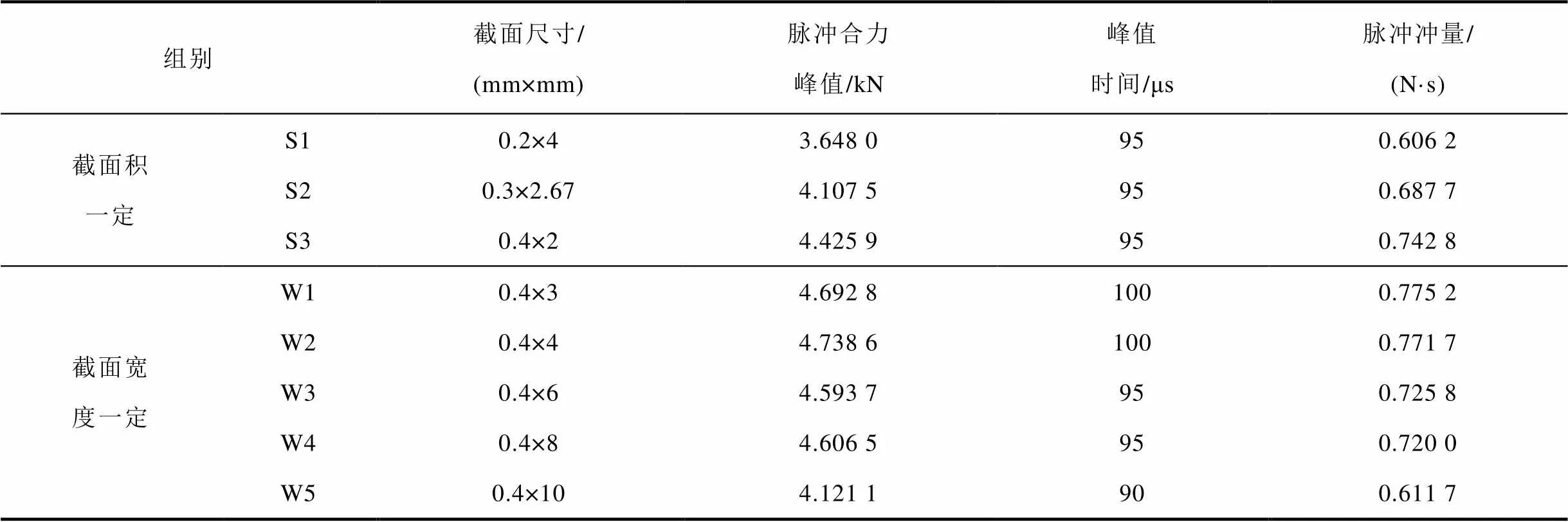
Tab.7 Impulse effect of coils with different cross-sectional dimensions

結合表7和圖12發現，當截面寬度保持一定時，脈沖線圈的電阻隨截面積增大而減小，脈沖電流峰值將增大，脈沖效果將有所提升。盡管脈沖電流總體呈增大趨勢，但隨著高度的進一步增加，越來越多脈沖電流分布在遠離目標物的區域，導致目標物上的磁感應強度不高。0.4 mm×2 mm、0.4 mm× 6 mm和0.4 mm×10 mm的線圈在脈沖力峰值時的磁感應強度和渦流密度分布如圖13所示，在目標物上僅表現磁感應強度，在線圈上表現渦流密度。脈沖量和脈沖力峰值及時間相關，一般情況下，線圈電阻減小，脈沖合力峰值和脈沖量增大。增大線圈截面高度提高電阻，其脈沖力峰值和脈沖量呈減小趨勢。因此，在保證耐流的前提下，需要對截面高度進行限制。

3.3 線圈匝間距

本文討論的0.4 mm×2 mm截面尺寸的線圈都屬于緊密繞制，如圖10所示。但由于漆層的存在，導致每匝之間存在間隙。在3.2節中所出現的0.2 mm×4 mm和0.3 mm×2.67 mm的脈沖線圈，若要在相同匝數下保證與0.4 mm×2 mm線圈具有相同的內、外徑結構，則需要通過改變線槽基底、繞制方法和漆層厚度等方法實現。

同樣對于0.4 mm×2 mm截面尺寸的線圈的匝間距，可以通過改變線槽基底來增大線圈的匝間距，從而改變線圈的內外徑。不同外徑和內徑線圈的脈沖效果見表8和表9。

表8 不同外徑線圈的脈沖效果

Tab.8 Impulse effect of coils with different outer diameters

表9 不同內徑線圈的脈沖效果

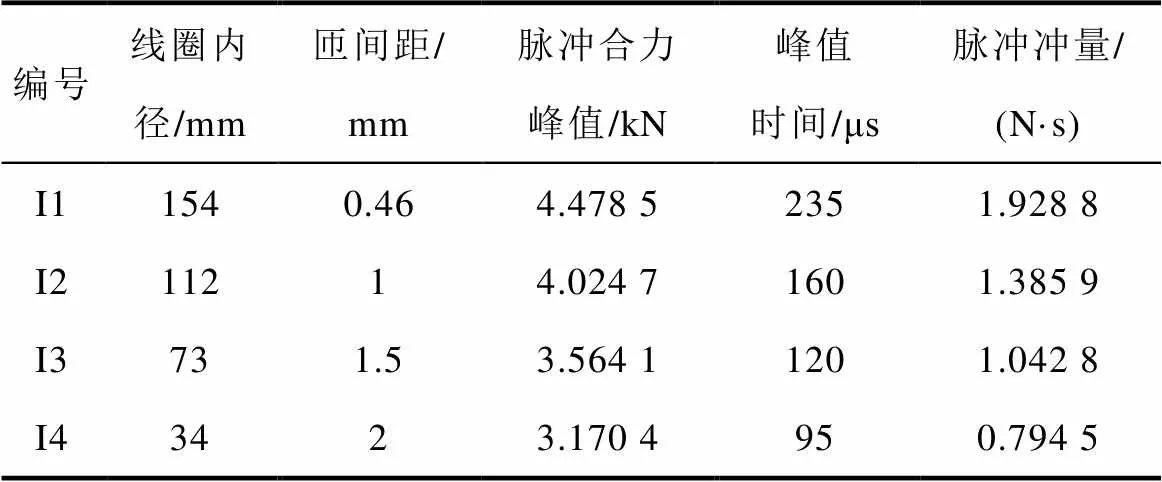
Tab.9 Impulse effect of coils with different inner diameters

1）表8中，保持線圈內徑為14 mm、匝數為40匝，通過改變匝間距來改變線圈外徑。隨著匝間距的增大，脈沖力合力峰值逐漸下降；而脈沖沖量在匝間距為1 mm時到達最大值，隨后開始逐漸下降。

2）表9中，保持線圈外徑為190 mm、匝數為40匝，通過改變匝間距，改變線圈內徑。脈沖合力峰值、峰值時間、脈沖沖量均隨著匝間距的增大而下降。

可見，當截面尺寸、匝數不變時，隨著匝間距的增大，脈沖力峰值和脈沖沖量均呈下降趨勢。故在線圈設計中，線圈的匝間距應該盡量減小。

此外，對比兩表結果，不同外徑下，電感、電阻隨匝間距的增加而增加；不同內徑下，電感、電阻的變化趨勢相反。表9中不同內徑線圈的電感、電阻較表8中的不同外徑線圈變化更大，表明其脈沖效果變化更為明顯，從而線圈外圈匝比內圈匝對電磁參數、脈沖效果的影響更大。

不同內、外徑下脈沖力密度隨向距離的變化如圖14所示，無論是在保持線圈外徑還是內徑的前提下，隨著匝間距的增大，脈沖力密度分布都更加平緩。保持內徑時，峰值時間較保持外徑時更短，脈沖力峰值更大；但保持外徑時，脈沖沖量更大，脈沖力作用時間更長。

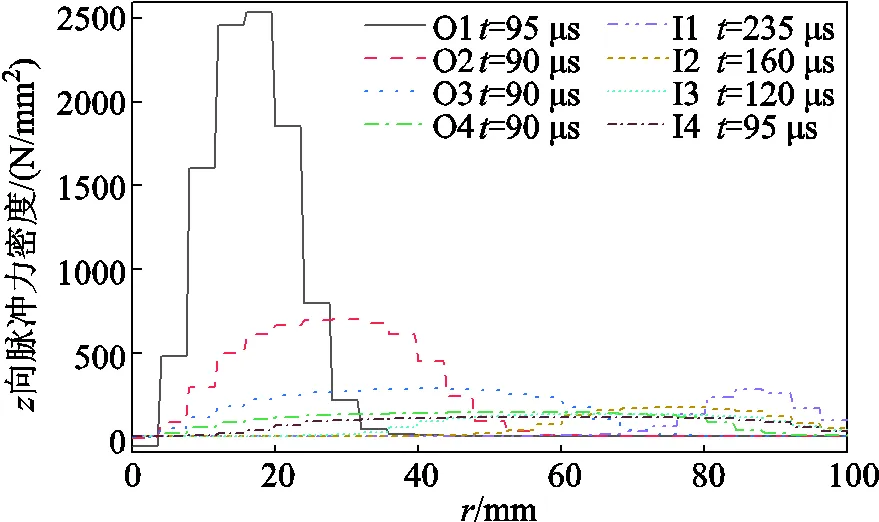
圖14 不同內、外徑下脈沖力密度隨距離的變化

3.4 小結

綜上所述，增加匝數、減小匝間距、增大每匝線圈的截面積和減小線圈高度將增大脈沖沖量。但過多的匝數會使脈沖力峰值下降，而當線圈超出目標物的范圍時，脈沖沖量將不會增加。據此，采用0.8 mm×2 mm的線徑繞制60匝，匝間距為1 mm，其內、外徑分別為72 mm、190 mm時，在同樣的電路參數條件下，脈沖合力峰值為6.992 9 kN，峰值時間為210 μs，脈沖沖量為2.591 6 N·s，能夠得到較大的脈沖合力峰值和脈沖沖量，取得較好的脈沖效果。

為了進一步檢驗所設計線圈的電脈沖除冰效果，考慮鋁板在葉片覆冰和防、除冰試驗中的相似性，有學者采用鋁板簡化真實機翼進行了防冰除冰試驗[21-22]。結合本文的仿真結果和實際條件，預先選擇尺寸長×寬×高為500 mm×500 mm×2 mm的6061鋁板作為除冰目標，在重慶大學人工氣候室內進行了覆冰鋁板的除冰試驗。當線圈匝數為60匝，放電電壓為DC 1 400 V，儲能電容為400 μF時，單次除冰動作即可完成10 mm雨凇的除冰，其除冰結果如圖15所示。

在優化脈沖線圈設計時，應以脈沖力峰值和脈沖沖量作為主要目標。同時考慮脈沖除冰不能改變目標物的外觀，脈沖力只能使目標物產生彈性應變、避免塑性應變等因素。結合單個線圈尺寸和線圈截面積的限制條件，通過調整線圈截面尺寸、線圈個數、線圈位置來限制目標物部分區域的脈沖力，從而在目標物表面產生彈性應變，進而有效除冰。

4 結論

1）在頻域計算中，有無目標物對脈沖線圈的電阻、電感影響較大，實際測量40、50、60匝脈沖線圈的電路參數和脈沖效果，驗證了模型的正確性。

2）匝數對線圈脈沖峰值力的影響存在極值；過度增加線圈高度反而會降低脈沖效果；線圈外圈匝比內圈匝對電磁參數、脈沖效果的影響更大。

3）需結合目標物材料、尺寸和覆冰等情況合理地限制線圈截面的高度，調整線圈的匝數、截面、匝間距及內、外徑，獲得較優的線圈結構參數，并且進行了相應的鋁板除冰驗證。

4）在本文的基礎上將開展優化脈沖線圈的結構動力學和除冰準則方面的研究，為進一步優化脈沖線圈，實現脈沖除冰應用微功耗化設計提供優化思路和技術路線。

[1] 蔣興良, 張志勁, 胡琴, 等. 再次面臨電網冰雪災害的反思與思考[J]. 高電壓技術, 2018, 44(2): 463-469. Jiang Xingliang, Zhang Zhijin, Hu Qin, et al. Thinkings on the restrike of ice and snow disaster to the power grid[J]. High Voltage Engineering, 2018, 44(2): 463-469.

[2] 歐陽虹, 蔣興良, 涂振華, 等. 磁浮接觸軌電脈沖除冰的試驗研究[J]. 高電壓技術, 2022, 48(4): 1553-1560. Ouyang Hong, Jiang Xingliang, Tu Zhenhua, et al. Experimental study on electro-impulse de-icing of maglev contact rail[J]. High Voltage Engineering, 2022, 48(4): 1553-1560.

[3] 李成祥, 石鑫, 周言, 等. 針對H型線圈的電磁脈沖焊接仿真及線圈截面結構影響分析[J]. 電工技術學報, 2021, 36(23): 4992-5001. Li Chengxiang, Shi Xin, Zhou Yan, et al. Electromagnetic pulse welding simulation for H-type coil and analysis of the influence of coil cross-sectional structure[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4992-5001.

[4] 周紋霆, 董守龍, 王曉雨, 等. 電磁脈沖焊接電纜接頭的裝置的研制及測試[J]. 電工技術學報, 2019, 34(11): 2424-2434. Zhou Wenting, Dong Shoulong, Wang Xiaoyu, et al. Development and test of electromagnetic pulse welding cable joint device[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2424-2434.

[5] Sophian A, Tian G Y, Taylor D, et al. Electromagnetic and eddy current NDT: a review[J]. Insight, 2001, 43(5): 302-306.

[6] 段志榮, 解社娟, 李麗娟, 等. 基于磁力傳動式陣列渦流探頭的管道缺陷檢測[J]. 電工技術學報, 2020, 35(22): 4627-4635. Duan Zhirong, Xie Shejuan, Li Lijuan, et al. Detection of defects in pipeline structures based on magnetic transmission eddy current array probe[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4627-4635.

[7] Park D G, Angani C S, Rao B C, et al. Detection of the subsurface cracks in a stainless steel plate using pulsed eddy current[J]. Journal of Nondestructive Evaluation, 2013, 32(4): 350-353.

[8] 陳龍龍, 魏曉光, 焦重慶, 等. 混合式高壓直流斷路器分斷過程電磁瞬態建模和測試[J]. 電工技術學報, 2021, 36(24): 5261-5271. Chen Longlong, Wei Xiaoguang, Jiao Chongqing, et al. Electromagnetic transient modeling and test of hybrid DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5261-5271.

[9] 程時杰, 陳小良, 王軍華, 等. 無線輸電關鍵技術及其應用[J]. 電工技術學報, 2015, 30(19): 68-84. Cheng Shijie, Chen Xiaoliang, Wang Junhua, et al. Key technologies and applications of wireless power transmission[J]. Transactions of China Electrotechnical Society, 2015, 30(19): 68-84.

[10] 金亮, 李育增, 楊慶新, 等. 大規模工程電磁場的億自由度可擴展并行計算方法[J]. 電工技術學報, 2022, 37(3): 589-598. Jin Liang, Li Yuzeng, Yang Qingxin, et al. Extensible parallel computing method with hundreds of millions of freedoms for large-scale engineering electromagnetic field[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 589-598.

[11] 王洋洋. 微功耗飛機電脈沖除冰系統理論與實驗研究[D]. 重慶: 重慶大學, 2020.

[12] Biro O, Preis K. On the use of the magnetic vector potential in the finite-element analysis of three-dimensional eddy currents[J]. IEEE Transactions on Magnetics, 1989, 25(4): 3145-3159.

[13] 李清英, 白天, 朱春玲. 電脈沖除冰系統的電磁場分析[J]. 南京航空航天大學學報, 2011, 43(1): 95-100. Li Qingying, Bai Tian, Zhu Chunling. Electromagnetic field analysis for electro-impulse de-icing system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(1): 95-100.

[14] Henderson R A. Theoretical analysis of the electrical aspects of the basic electro-impulse problem in aircraft de-icing applications[D]. Wichita: Wichita State University, 1986.

[15] Zumwalt G W, Schrag R L, Bernhart W D, et al. Electro-impulse de-icing testing analysis and design[R]. NASA Contractor Report 4175, 1988.

[16] Moehle E, Haupt M, Horst P. Coupled magnetic and structural numerical simulation and experimental validation of the electro impulse de-icing[C]//54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, Massachusetts, USA, 2013: 1494.

[17] 郭濤. 機翼電脈沖除冰系統電磁力及其除冰過程仿真研究[D]. 南京: 南京航空航天大學, 2017.

[18] 王洋洋, 蔣興良. 邊光滑有限元-邊界元耦合法計算二維瞬態渦流場[J]. 哈爾濱工業大學學報, 2021, 53(3): 137-141, 151. Wang Yangyang, Jiang Xingliang. Calculation of 2D transient eddy current field by ES-FEM-BEM coupling method[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 137-141, 151.

[19] Huang Tingfan, Jiang Xingliang, Chen Yu, et al. Experimental study on electro-impulse de-icing of wind turbine blades[C]//2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 2021: 205-209.

[20] 黃廷帆. 金屬表面覆冰的電磁脈沖除冰方法研究[D]. 重慶: 重慶大學, 2021.

[21] Wang Yangyang, Jiang Xingliang. Design research and experimental verification of the electro-impulse de-icing system for wind turbine blades in the Xuefeng mountain natural icing station[J]. IEEE Access, 2020, 8: 28915-28924.

[22] Chen Long, Yang Qingbao, Yang Xue, et al. Numerical investigation of heat transfer performance of graphene-doped anti-/deicing component[J]. Thermal Science and Engineering Progress, 2022, 28: 101098.

Study of the Effect of Pulsed Coil Structures on Transient Electromagnetic Fields for Aircraft and Wind Turbine Blade De-Icing

Chen Yu1Jiang Xingliang1Huang Tingfan1,2Jiang Tao1Hu Qin1

（1. Xuefeng Mountain Energy Equipment Safety National Observation and Research Station of Chongqing University Chongqing 400044 China 2. Army Engineering University of PLA Chongqing 400044 China）

Electro-impulse de-icing of atmospheric structures is a low-power consumption and fast de-icing method. Pulsed coil is a key component in the conversion of energy for electro-impulse de-icing. Of which the structural parameters need to be optimized, so as to improve the de-icing effect of the electro-impulse de-icing system and promote the development of the system’s low-power consumption and lightweight.

Most researches on pulsed coil at home and abroad focus on the electrodynamics, structural dynamics and de-icing effect on the target. However, the influence of different structural parameters on the transient electromagnetic fields and impulse effects of pulsed coils has been little studied.

Aiming at the above problems, this paper started from the basic principle of circuit and electromagnetic field, simplified the electro-impulse de-icing system, deduced the field-circuit mathematical equation of pulsed coil, established the physical model of pulsed coil and rectangular cross section target, and determined the circuit parameters, the governing equation and boundary conditions of transient electromagnetic field. Based of which, the calculation methods of magnetic induction intensity, target eddy current, impulse force and impulse were obtained. The transient electromagnetic field of the pulsed coil is analyzed by finite element software, and the time-varying characteristics of the pulsed coil’s electromagnetic parameters were obtained.

In this paper, the electrical parameters and transient electromagnetic fields under different coils were calculated, which shows that the presence of the target had a great influence on the resistance and inductance of the pulsed coil. The circuit parameters and impulse effects of 40, 50 and 60 turns pulsed coils are measured by the impact pendulum test, which verifies the correctness of the model. Through comparative analysis, it is found that :(1) the number of turns has a great influence on the peak value of the pulse force. With the increase of the number of turns, the impulse effect gradually increases. However, the gradual increase in the outer diameter of the coil leads to an increase in coil impedance and a decrease in pulse frequency, making it impossible to achieve de-icing at high strain rates, in particular, the outer diameter of the coil exceeding the outer diameter of the target. (2) Excessive increase in coil height will reduce the impulse effect. With the increase of the coil height, the non-uniform distribution characteristics of the pulse current in the coil become more obvious, especially the pulse current density in the area far from the target increases, resulting in the reduction of the impulse effect. (3) With the increase of the coil turn-to-turn distance, the distribution of the pulsed coil is wider, which makes the pulse force on the target more uniform, but the peak of the pulse force density still appears in the middle region of the coil. (4) The outer turns of the coil have greater influence on electromagnetic parameters and impulse effect than the inner turns.

By reasonably limiting the height of the coil cross-section and adjusting the number of turns, cross-section, turn-to-turn distance and inner and outer diameter of the coil in combination with the target material, dimensions and icing, the optimal structural parameters of the pulsed coil under fixed circuit parameters were obtained (60 turns winding, 0.8 mm×2 mm wire diameter, 1 mm turn spacing, 72 mm inner diameter and 190 mm outer diameter).

Under the initial conditions of=400 μF and0=DC 1 200 V, the pulse force of 6.992 9 kN on the target, with a peak time of 210 μs and a pulse impulse of 2.591 6 N·s. The corresponding de-icing tests on aluminum plates were carried out using the above pulsed coil with good de-icing results.

Pulsed coil, transient electromagnetic field, impulse effect, structural parameters

陳 宇 男，1996年生，博士研究生，研究方向為輸電線路覆冰與防冰。E-mail：cqueecy@cqu.edu.cn（通信作者）

蔣興良 男，1961年生，博士，教授，博士生導師，研究方向為能源裝備安全與災害防御。E-mail：xljiang@cqu.edu.cn

10.19595/j.cnki.1000-6753.tces.220883

TM8; TM15

重慶市技術創新與應用發展專項重點項目（cstc2021jscx-dxwtBX0001）和南方電網有限責任公司防冰減災重點實驗室支撐項目（GZKJXM20190748）資助。

2022-05-23

2022-08-07

（編輯 李 冰）