基于GA-FUZZY-PID算法的精準施肥控制系統研究

王昊，張立新，吳勛，王夢帆，李靖，閆梓洋

（石河子大學機械電氣工程學院，新疆 石河子 832000）

0 引 言

棉花作為紡織業的主要原材料，是一種與國家經濟發展密切相關的戰略資源。相關數據表明，在2022年，新疆地區的棉花產量539.1 萬t，占全國棉花總產量的90%以上，是我國最大的棉花產區[1]。棉花生長發育過程需要大量用水、大量用肥，但新疆地區年均蒸發量遠大于年均降水量，水資源嚴重短缺。針對這一問題，新疆地區棉田灌溉采用水肥一體化技術[2]。

水肥一體化技術是一種廣泛應用于新疆棉花種植的節水節肥新技術。水肥一體化技術的原理是通過對棉田內傳感器所獲取的監測數據進行智能化分析和處理，利用智能算法推導出灌溉決策并反饋至終端執行。該技術實現了棉田水肥精準施肥，提高了土壤的水肥利用效率，達到保護環境、提高產量、節省勞力的效果[3]。

目前水肥一體化技術的控制方法主要集中在PID控制算法與模糊控制算法。但傳統PID算法對于時變對象和非線性系統的處理性能差，易引起超調，產生振蕩[4]；模糊算法中參數設定大多基于人工經驗，存在控制欠細膩的問題。因此，通過結合遺傳算法計算簡單、功能強、優化效果好的特點，實現對肥料流量快速有效的調整，降低了流量調節過程中時滯性、非線性等因素帶來的影響[5]。

1 棉田施肥灌溉系統總體結構

棉田施肥灌溉系統主要由蓄水池、儲肥罐、過濾器、電磁閥、流量傳感器、壓力表、軟管泵等裝置組成，棉田施肥灌溉系統總體結構圖如圖1所示。其中，儲肥罐的過濾器兩端安裝了壓力表，用于判斷過濾器的堵塞情況，實現定期對過濾器的清洗更換，防止肥料中的固體沉積物堵塞管道[5]。灌溉管道上安裝有穩壓器，確保灌溉時管路的壓力穩定。各管道均裝有單向閥，防止管內液體的倒流。在灌溉管道上裝有流量計，用以監測灌溉流量。施肥系統的輸送裝置選擇軟管泵，三相異步電動機與軟管泵泵體相連，被輸送物料由軟管包圍，不與其他零件接觸。當轉子轉動時，隨著滾輪位置的變化，軟管被壓縮和回彈，使泵產生吸入和壓出作用，達到輸送肥料的目的。系統通過改變與軟管泵相連的變頻器的頻率來精確調節軟管泵出口的施肥流量。

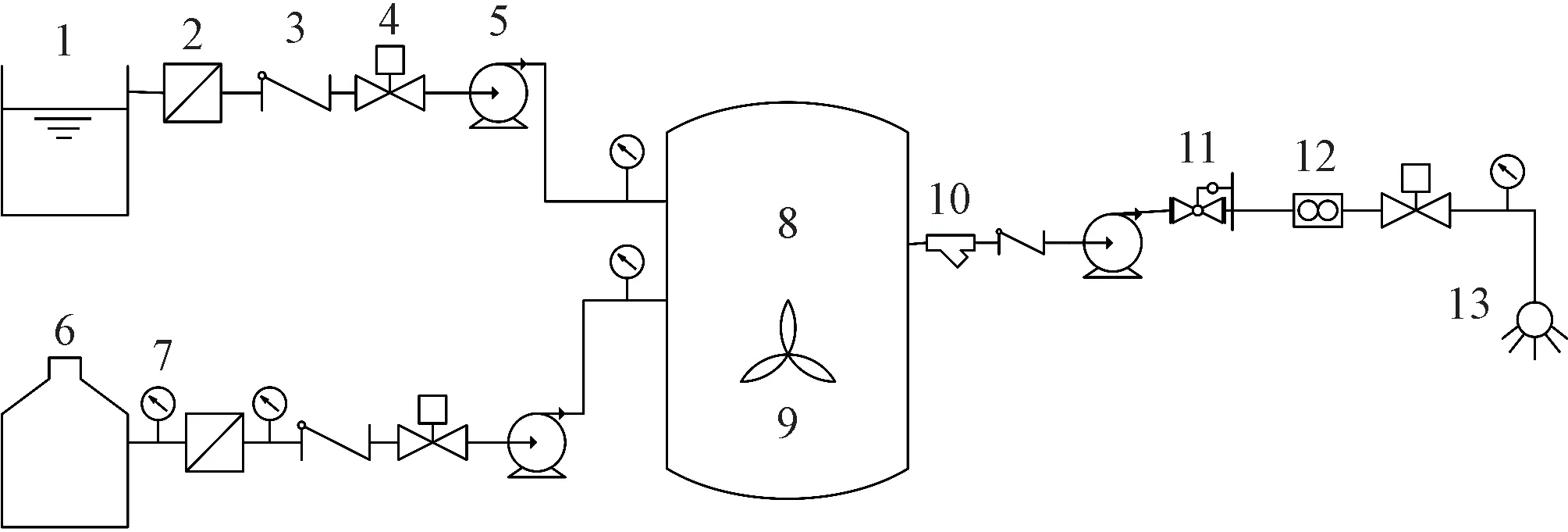
圖1 棉田施肥灌溉系統結構Fig.1 Structure diagram of cotton field fertilization and irrigation system

棉田施肥灌溉系統的工作流程如下：將蓄水池和儲肥罐的電磁閥開啟，相應線路的軟管泵將水和肥料按比例抽入混肥罐中，通過攪拌泵進行攪拌混合，當攪拌混合結束后，混合肥液由灌溉管道的軟管泵輸送到棉田。當灌溉管道上的流量傳感器監測到肥料流量與設定值出現偏差時，系統將自動調整混合罐出口處軟管泵流量，以保持穩定狀態。

2 棉田施肥灌溉系統控制模型建立

基于施肥灌溉的特性和系統的復雜程度，選擇一階慣性加延遲環節的傳遞函數作為數學模型[4,5]，數學模型方程如下：

式中：K為增益系數；τ為延遲時間；T為時間常數；s為復頻率。

將施肥流量的期望值作為開環系統的輸入，采樣時間間隔設定為1 s，獲得流量變化的數據。采用一階近似方法，在Matlab軟件中對數據進行擬合，得到系統的增益系數K為0.06、延遲時間τ為8 s、時間常數T為28。

2.1 PID控制器設計

PID控制器由比例部分、積分部分、微分部分組成，具有操作簡單、魯棒性高等優勢，在工業領域具有廣泛的應用[6]。在實際應用過程中，控制器輸入常為設定值r(t)與輸出值y(t)之差e(t)，輸出控制量u(t)由差值e(t)決定，輸出控制量u(t)具體表達式如下：

式中：Kp為比例增益；Ti為積分時間常數；Td為微分時間常數。

采用Cohen-Coon參數整定法初步整定KP、Ti、Td3個參數。Cohen-Coon參數整定法的主要工作原理如下：通過配置系統的主導極點使對象的過渡曲線按4∶1的衰減率衰減，從而得到最優的PID參數整定值[7]。參數整定經驗公式如下：

根據棉田施肥灌溉系統的數學模型，將對應參數值代入式（3）中，并通過試湊法對PID的各系數進行調整，使設定量與反饋量之間的誤差不斷減小直至滿足系統要求。參數最終設定為：Kp=20，Ki=2，Kd=12。其中，Ki為積分增益，Ki=Kd為微分增益，

2.2 模糊算法優化設計

模糊PID控制器是通過模糊算法對PID控制器參數進行動態調整，使系統達到良好的控制效果。本文設計的模糊優化系統為雙輸入三輸出系統，模糊控制方法為Mamdani直接推理法，即模糊控制規則共由49條語句構成，但實際的輸入數據僅與其中4條語句有關，利用這4條被激活的語句進行推理計算得到控制目標的輸出量[8]。模糊控制器決策模型如圖2所示。

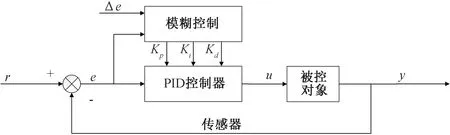
圖2 模糊控制器決策模型ΔeFig.2 Fuzzy controller decision model

該決策模型的輸入變量為流量偏差值e和流量偏差變化率Δe，輸出變量為比例增益Kp、積分增益Ki、微分增益Kd。流量偏差值e和流量偏差變化率Δe的量化因子為K1、K2，比例增益Kp、積分增益Ki、微分增益Kd的比例因子為K3、K4、K5。設定流量偏差值e和流量偏差變化率Δe的模糊論域為[-2, 2]，根據相關經驗，則量化因子K1=1、K2=1；比例增益Kp、積分增益Ki、微分增益Kd的模糊論域均為[-3, 3]，量化因子分別設定為K3=5、K4=0.6、K5=3。輸入輸出變量的模糊集論域分為7個模糊集合，分別由NB（負大）、NM（負中）、NS（負小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）語言值來表示[9]。模糊控制規則根據專家經驗給出，比例增益Kp、積分增益Ki、積分增益Kd的控制規則分別如表1～表3所示。

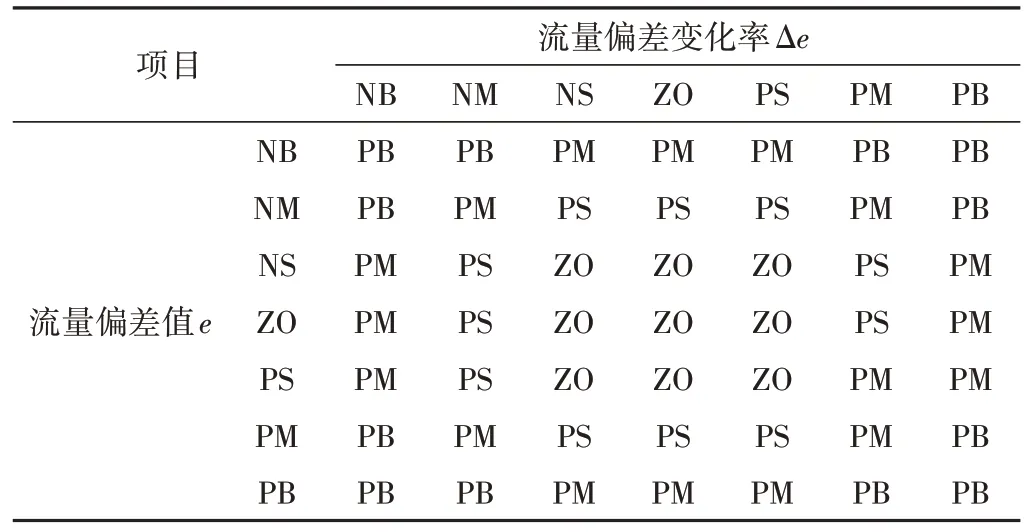
表1 比例增益Kp的控制規則Tab.1 Control rules for proportional gain Kp

表2 積分增益Ki的控制規則Tab.2 Table of control rules for integral gain Ki

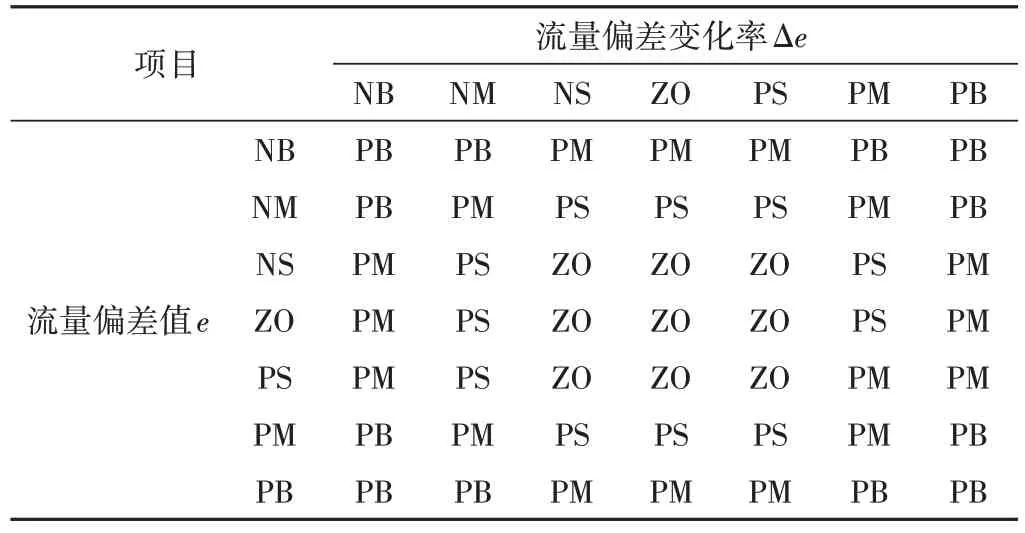
表3 微分增益Kd的控制規則Tab.3 Table of control rules for integral gain Kd

實際控制過程中，單條模糊控制規則對應的模糊推理語句為多重多維條件語句，其基本形式為：

公式（4）表明若流量偏差值e的輸入語言值為A，流量偏差變化率Δe的輸入語言值為B，則根據模糊規則推理，比例增益Kp的輸出語言值為C，積分增益Ki的輸出語言值為D，微分增益Kd的輸出語言值為E。總的模糊控制規則R是49條多重多維條件語句的并運算。為提高系統的靈敏度，系統模糊控制器的輸入輸出量均采用三角形隸屬度函數。流量偏差值和流量偏差變化率的隸屬度函數如圖3所示，比例增益Kp、積分增益Ki、微分增益Kd的隸屬度函數如圖4所示，比例增益Kp、積分增益Ki、微分增益Kd的特性曲面分別如圖5～圖7所示。

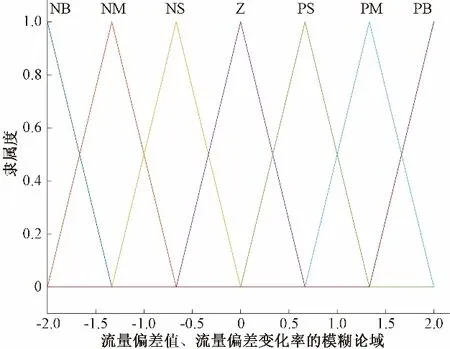
圖3 流量偏差值e和流量偏差變化率Δe的隸屬度函數Fig.3 The membership function of flow deviation value e and flow deviation change rate Δe

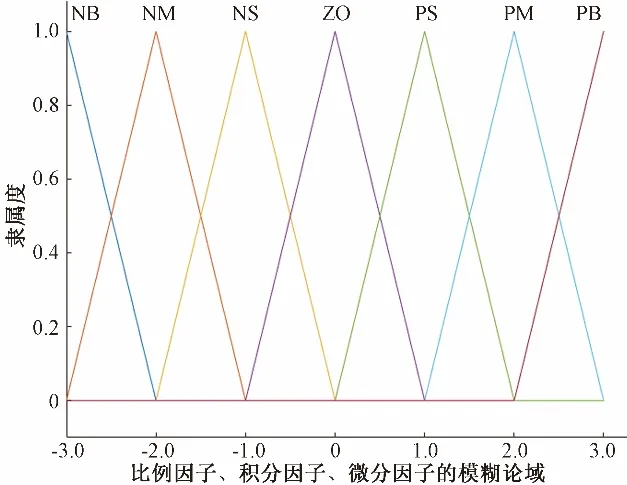
圖4 比例增益Kp、積分增益Ki、微分增益Kd的隸屬度函數Fig.4 Membership functions of proportional gain Kp, integral gain Ki,and differential gain Kd

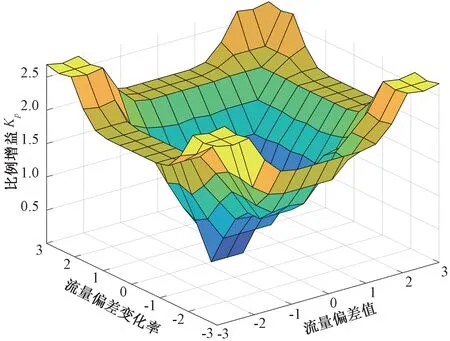
圖5 比例增益Kp的特性曲面Fig.5 Characteristic surface of proportional gain Kp

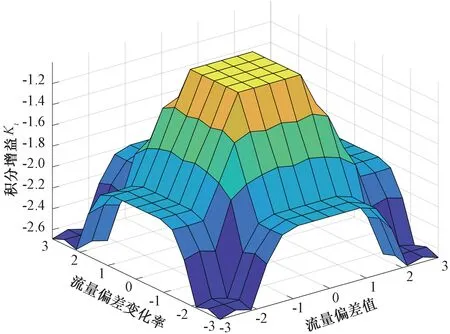
圖6 積分增益Ki的特性曲面Fig.6 Characteristic surface of integral gain Ki

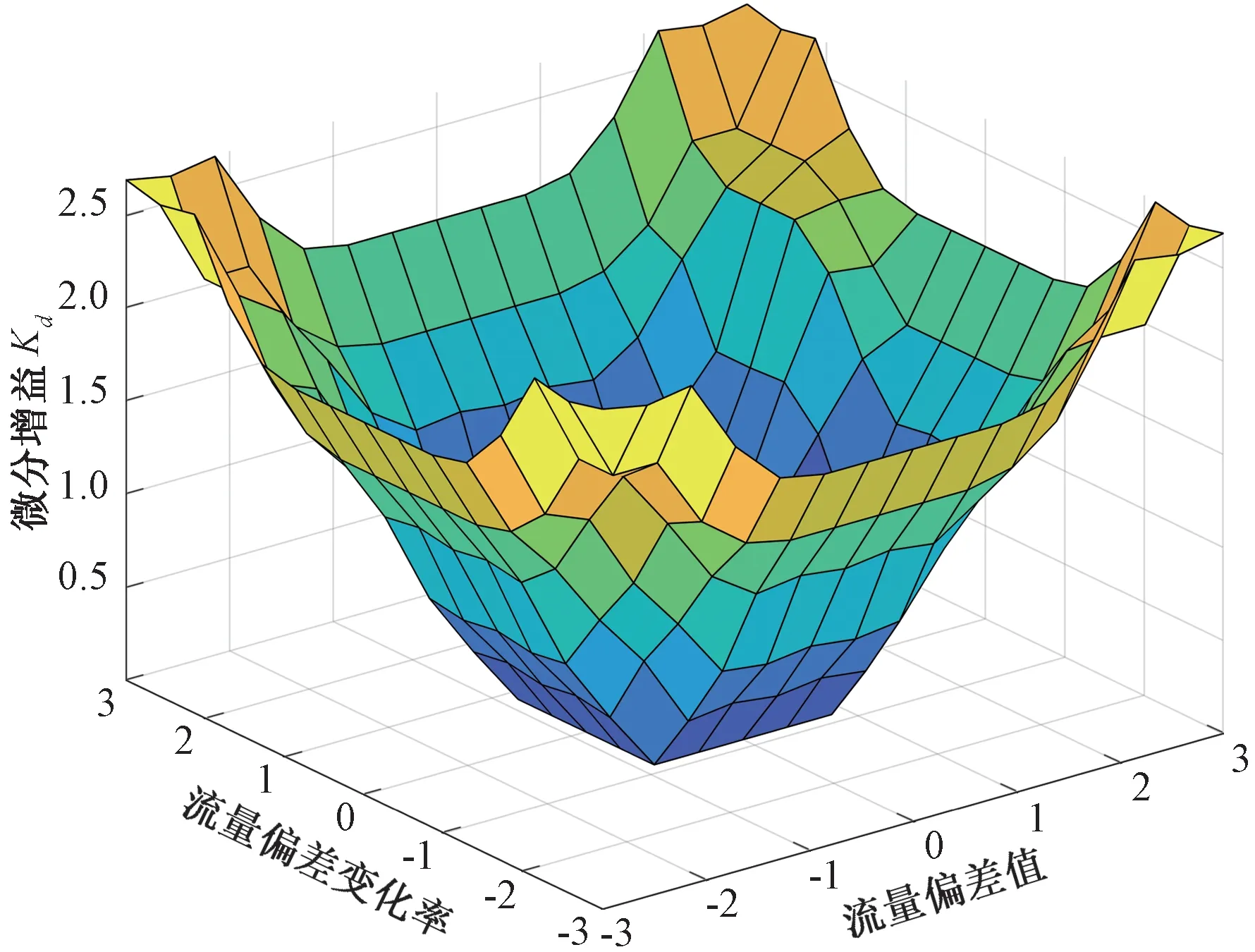
圖7 微分增益Kd的特性曲面Fig.7 Characteristic surface of differential gain Kd

系統的清晰化方法選用重心法，其公式如下：

式中：K(i)表示某一輸出變量模糊集合的隸屬函數有值處；P為隸屬函數有值處的個數；μk(i)為有值處的隸屬函數值。

2.3 遺傳算法優化設計

遺傳算法作為一種高效啟發式算法，具有隱藏的并行性，是從解空間中多個體出發，尋找最優解的算法，具有高效穩定的特點，在自動控制、圖像處理、生產調度問題等方面有著廣泛應用[9]。圖8為遺傳算法流程圖。

圖8 遺傳算法流程Fig.8 Flow chart of genetic algorithm

（1）初始種群。使用遺傳算法對比例因子K3、K4、K5進行優化，編碼方式采用浮點數編碼方法，將K3、K4、K5編為三維列向量，以提高運行效率，初始種群為隨機生成的20個初值。

（2）適應度函數。適應度函數體現了個體的優劣性，為選擇提供了標準與動力[10]。控制器的瞬態性能指標主要有上升時間、穩態時間、最大超調量[11]。上升時間、穩態時間反映了控制器的響應速度，最大超調量反映了控制器控制過程的穩定性。針對文中確定的模型而言，誤差函數W公式如下：

式中：T表示使用PID算法輸出到達設定值的時間；y(t)表示系統實時最終輸出值；y0表示目標函數的設定值；tα表示使用優化算法后輸出最終到達設定值并平衡的時間；ym表示系統最終輸出的最大值。

根據專家經驗及實踐，當系統越差時，誤差W值將越大，個體保留至下一代的可能就越小，因此可采用誤差W作為目標函數來評價系統的性能，設置系統的適應度函數等于目標函數，將問題轉換成求適應度函數最值問題。適應度函數計算公式為：

（3）選擇操作。是指在生物遺傳進化過程中，使適應度更強的個體遺傳到下一代的機率更大，選擇的主要目的是避免基因缺陷，提升全局的收斂性與計算效率。本文使用的選擇機制為常規的輪盤賭選擇法，即個體的適應度函數值越小，被選擇的概率就越大。

（4）交叉操作。是指群體內的個體隨機兩兩配對，以一定概率交換部分染色體。通過2個染色體的交換組合，產生新的優良品種。本文使用的交叉機制為單點交叉，即隨機設置一個交叉點，在該點后字符相互交換，設定交叉概率為0.6。

（5）變異操作。是指以一定概率隨機改變個體中某個串的位置，防止丟失一些有用的遺傳因子，決定了遺傳算法的局部搜索能力，設定變異概率為0.1。

終止條件：遺傳算法可通過對最大迭代次數的設定或使適應度函數到達特定范圍來終止程序運行。本文采用設定最大迭代次數作為終極條件，設定迭代次數為100代，最終通過解碼得到最優解。3種不同的初始設定值在100次迭代過程中的適應度函數變化曲線如圖9所示。

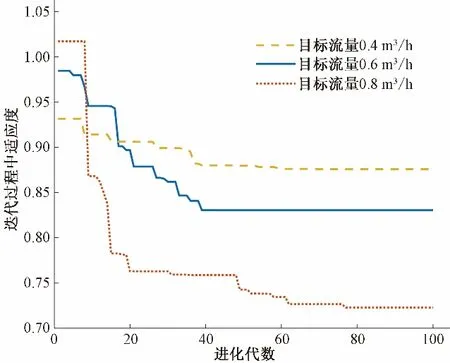
圖9 不同設定流量值的迭代過程中適應度函數變化曲線Fig.9 Adaptability function change curve during iteration with different set flow values

3 仿真分析

為驗證本文設計的GA-Fuzzy-PID算法策略的優越性，在Simulink中分別搭建了PID控制器、Fuzzy-PID控制器、GAFuzzy-PID控制器模型，如圖10所示，并對仿真結果進行比較。在棉花實際灌溉過程中，流量選擇{0，1 m3/h}，因此算法應適應范圍內任一流量設定值[12]。當設定流量值在該范圍內取值時，為驗證GA-Fuzzy-PID算法是否優于其他2種算法，選取目標流量值為0.6 m3/h、0.8 m3/h、0.4 m3/h 3種不同目標設定流量值進行仿真，0.6 m3/h的仿真結果如圖11所示，并給出3種不同設定流量值的性能指標如表4～表6所示，討論不同設定目標流量值下3種算法的性能指標。

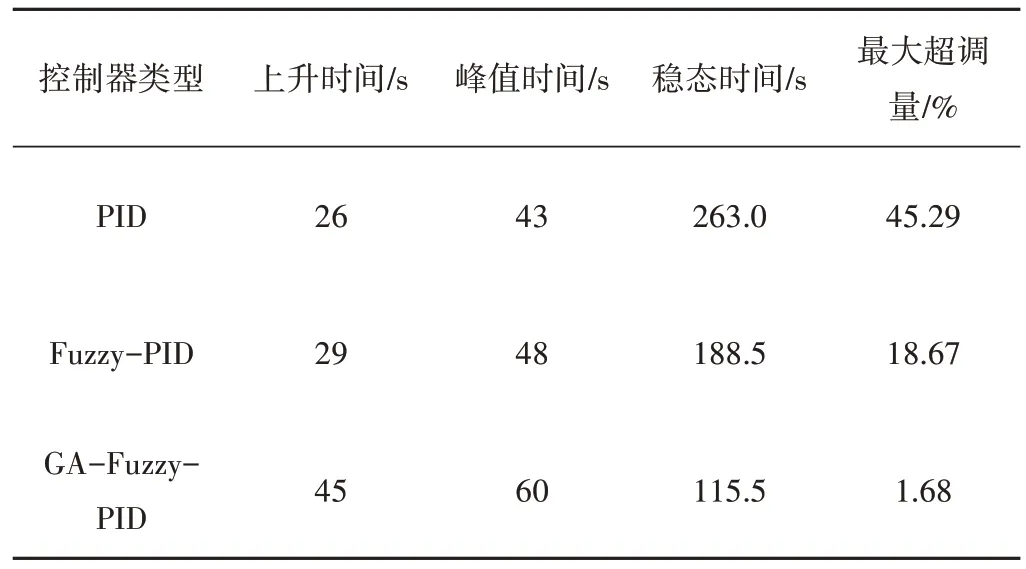
表4 設定流量值為0.6 m3/h時的3種控制器性能指標Tab.4 Three controller performance indicators when the flow rate is set to 0.6 m3/h

圖10 Simulink控制系統模型Fig.10 Simulink control system model diagram

在設定流量值為0.6 m3/h的情況下，如表4所示，PID最大超調量為45.29%，穩態時間為263.0 s，遠落后于其他2種算法。Fuzzy-PID算法的使用，使得最大超調量穩定在18.67%，穩態時間在188.5 s，相對于PID算法降低了系統最大超調量，縮短了穩態時間。GA-Fuzzy-PID算法的最大超調量則降低至1.68%，穩態時間分別縮短至115.5 s，表明使用遺傳算法對Fuzzy-PID算法優化效果明顯。

在設定流量值為0.8 m3/h的情況下，如表5所示，PID最大超調量為43.30%，遠高于其他2種算法。穩態時間為279.0 s，遠落后于其他2種算法。Fuzzy-PID算法的最大超調量穩定在17.59%，穩態時間在197.5 s，表明算法具有良好性能。GA-Fuzzy-PID算法的最大超調量則減少至0.87%，穩態時間縮短至120.0 s，表明GA-Fuzzy-PID算法在大流量設定值時，能夠適應設定流量值的變化。

在目標流量為0.4 m3/h的情況下，如表6所示，PID最大超調量為42.35%，穩態時間為248.0 s。Fuzzy-PID算法的最大超調量穩定在19.74%，穩態時間為207.0 s，相對于PID算法性能有所提升。GA-Fuzzy-PID算法最大超調量減少至4.14%，穩態時間縮短至147.0 s，表明GA-Fuzzy-PID算法在低設定流量值時，仍具有優越性。

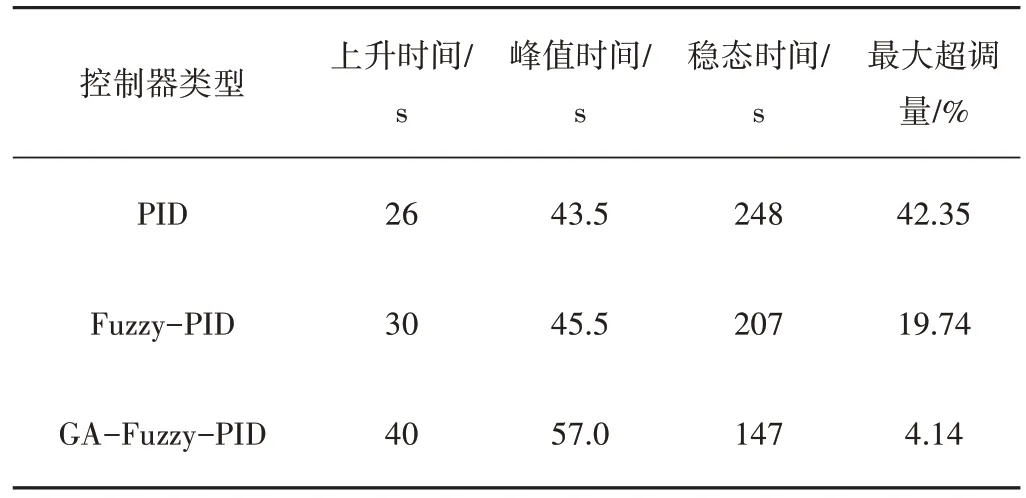
表6 設定流量值為0.4 m3/h時的3種控制器性能指標Tab.6 Three controller performance indicators when the flow rate is set to 0.4 m3/h

由表4～表6可知，PID算法表現差，3種不同設定流量值下的最大超調量均在40%以上，穩態時間在240 s以后，性能指標遠落后于其他2種算法。Fuzzy-PID算法的使用，使得最大超調量穩定在20%以內，穩態時間在200 s左右，相對降低了系統最大超調量，縮短穩態時間，具有良好的工作性能。GA-Fuzzy-PID算法的使用，使得最大超調量穩定在5%以內，表明GA-Fuzzy-PID算法具有更好的調控系統，避免系統嚴重過沖。穩態時間穩定在150 s以內，表明GA-Fuzzy-PID算法響應速度快，能快速將系統調整到設定狀態上。在設定流量值的范圍內，GA-Fuzzy-PID算法能夠適應設定流量值的變化，具有優異的性能。

4 精準施肥控制系統流量調節實驗

為了驗證GA-Fuzzy-PID算法的實用性能，本文搭建了相應的流量調節實驗平臺，以STM32F103ZET6單片機為控制元件，將I/O口接收的流量傳感器的信號在單片機內部進行運算，轉換成可變化的電壓信號，對變頻器的輸出頻率作出調整，最終改變混合罐出口處的肥料流量。軟管泵的最大輸送流量為1 m3/h，額定功率為1.5 kW，額定電壓為380 V。變頻器額定功率為2.2 kW，輸出頻率為0～400 Hz，額定電壓為380 V。流量傳感器選擇美控中國的不銹鋼電磁流量計，型號為LDG-MIK，精度為0.5%。操作過程中將混合罐中液體的體積保持在50 L。流量調節實驗平臺如圖12所示。

圖12 實驗平臺Fig.12 Test platform

本次實驗設定流量為0.6 m3/h，對PID控制器、Fuzzy-PID控制器、GA-Fuzzy-PID控制器進行測試。實驗結果如圖13所示，3種控制器性能指標如表7所示。

表7 實驗流量值為0.6 m3/h時的3種控制器性能指標Tab.7 Three controller performance indicators at a test flow rate of 0.6 m3/h

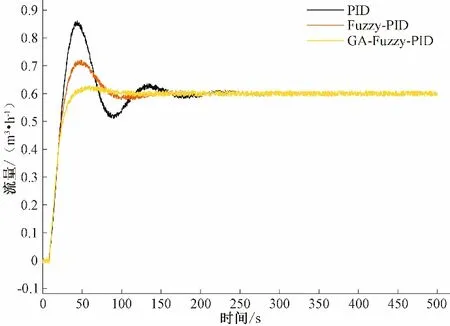
圖13 實驗流量為0.6 m3/h時3種控制器的調控曲線Fig.13 Control curves of three controllers at a test flow rate of 0.6 m3/h

實驗設定目標流量為0.6 m3/h，性能指標如表7所示，PID算法的最大超調量為41.93%，穩態時間為257.1 s，遠落后于其他2種算法。Fuzzy-PID算法的使用，使得最大超調量穩定在20.07%，穩態時間在182.4 s，相對于PID算法降低了系統最大超調量，縮短了穩態時間。GA-Fuzzy-PID算法的最大超調量則降低至4.41%，穩態時間縮短至126.3 s，說明使用遺傳算法優化后的Fuzzy-PID控制器具有優異的性能。

5 結 論

（1）本文設計了一套基于GA-Fuzzy-PID算法的控制系統，采用遺傳算法對Fuzzy-PID算法中的3個量化因子進行優化，通過求解適應度函數的極值，得到最優編碼基因，經解碼處理獲得優化后的量化因子，進而提升系統的魯棒性和精度。

（2）通過Matlab軟件仿真與實驗驗證表明：相較于PID控制器、Fuzzy-PID控制器，GA-Fuzzy-PID控制器的性能指標均遠遠優于其他2種算法。在設定的流量范圍內，本文設計的GA-Fuzzy-PID控制動態性能更佳，更適于棉田施肥精準控制。