基于機理分析的草原放牧策略研究
于和碩
(上海理工大學機械工程學院,上海 200093)
0 引言
在草原放牧的過程中,通常需要考慮兩個因素,分別是放牧方式和放牧強度。放牧方式和放牧強度選擇的不同,結果也會不同。植物的生長除了受自身生長規律的影響外,還有外界刺激的影響。當牧羊采食牧草時,地上的生物量會減少,同時,植物有著超補償生長的特點,適當放牧有利于植物的生長,進而改善土壤質量,而過度放牧則會導致植被破壞,增大土地裸露面積,甚至導致土壤板結化、土地沙漠化,使得土壤肥力下降,危害環境。
內蒙古錫林郭勒草原是國家最重要的畜牧業產業基地之一,也是北方綠色生態走廊。因此,為錫林郭勒草原構建一個基于放牧策略對環境影響關系的模型對于保護其環境生態系統具有重要的意義。
1 樣本數據處理
近年來,科研工作者在內蒙古自治區錫林郭勒盟草原上選取代表性草場進行了大量的實驗,采集了不同牧戶生態畜牧業模式群落樣方調查數據以及不同示范牧戶牲畜數量調查數據;還有不同放牧強度土壤碳氮監測數據、輪牧放牧樣地群落結構監測數據。
基于這些數據,首先從計算的角度,對公式進行分析和推導,建立微分方程,分析內部機理。然后進行數據挖掘,對數據預處理如描述性統計分析,采用單因素方差分析確定放牧策略對土壤有機物含量均值的影響。
1.1 放牧策略與植被生物量的數學模型
對于放牧與植物生長之間的關系,Woodward 等建立了如下一個簡單模型[1]:
其中,w為植被生物量,S為單位面積的載畜率。
查閱相關文獻所給的土壤—植被—大氣系統的水平衡基本方程[2-5]:
其中,ΔW 為土壤貯水變化量,Wt+1和Wt分別為時間段內的始末土壤含水量,P為降水量,Gu和Gd分別為地下水毛管上升量和土壤水滲透量,Eta為實際蒸發量,Rin和Rout分別為入和出徑流量,ICstore為植被截流量,其表達式為:
其中,cp為植被覆蓋率,ICmax為特定植被的最大截流量(mm),k 為植被密度校正因子,與LAI 有關,Rcum為累積降雨量(mm)。ICmax可以通過LAI來估算:
其中,LAI為一個分布式的時變參數。根據研究表明,當地下水埋深度大于4m 后,毛管上升水對2m 土壤水分循環的作用很小。草原地下水埋藏較深,地下水毛管上升量對根系層的補給量也可忽略,則有Wt=W0,故⑵式簡化為式⑸[4]:
植被覆蓋率的公式如下:
式⑴~式⑹,即是生物量與放牧策略之間的關系。
1.2 放牧策略與土壤物理性質的數學模型
植被截流量表達式為:
其中,牧區供水率(主要為降水)為P;地表蒸散發率為E;土壤含水量為β;土壤植被覆蓋率為α*G(w);成草數量為w;草原的蓋度為G(w)=(1-e-εgw/w*);枯萎率為D=β*(eεgw/w*-1),其中w*是該草原群落的特征值。對式⑺積分可得式⑻:
式⑻即為放牧策略與土壤物理性質之間的關系。
1.3 數據統計分析
根據上述所示的模型,進行數據驅動的機理分析。根據提供的數據,計算不同的放牧策略對土壤有機物含量均值的影響。土壤有機物含量均值如表1所示。
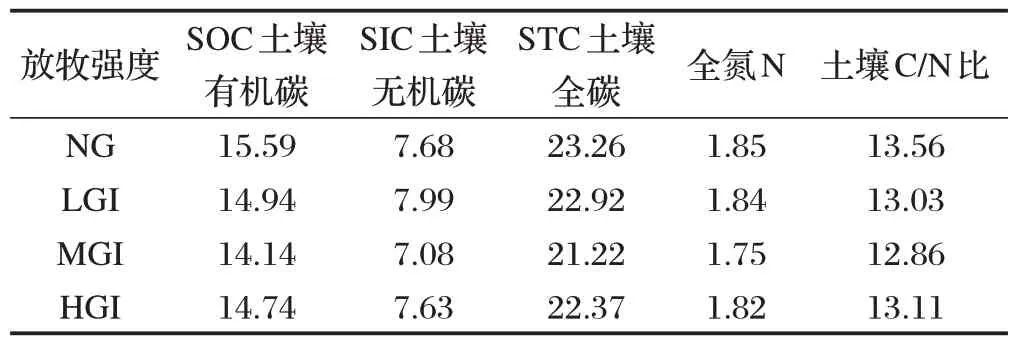
表1 不同的放牧策略對土壤有機物含量均值的影響
根據表1 可以看出,土壤有機物含量的均值差異可能與放牧策略的不同有關。要探究不同的放牧策略是如何對土壤有機物含量的影響,我們要做一下單因素方差檢驗,看一下究竟是否存在顯著差異。
分析具體步驟不詳細展開,分別對不同放牧強度中的SOC 土壤有機碳、SIC 土壤無機碳、STC 土壤全碳、全氮N以及土壤C/N比進行平均值檢驗,檢驗結果如表2所示。
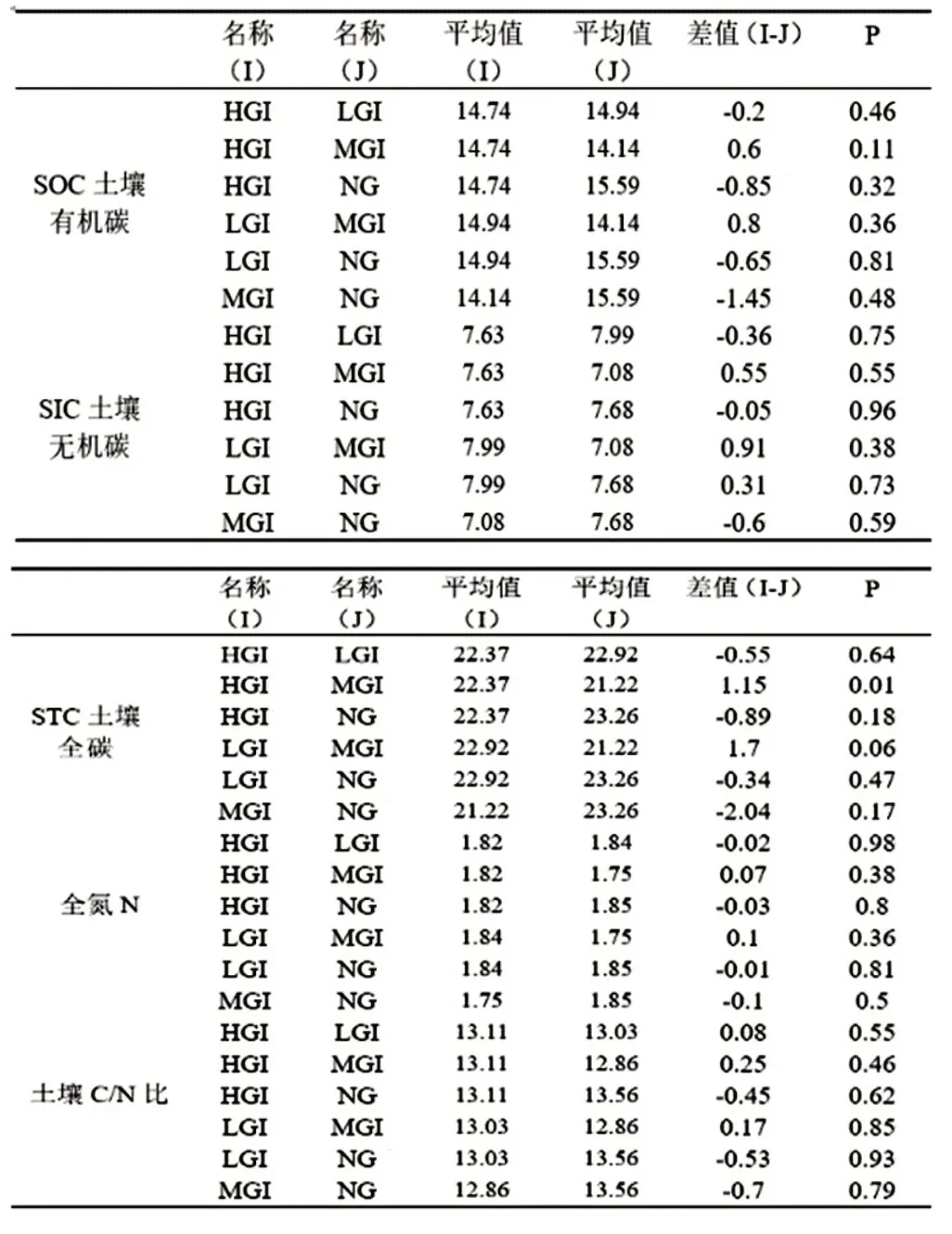
表2 不同的放牧策略對土壤有機物含量均值的影響
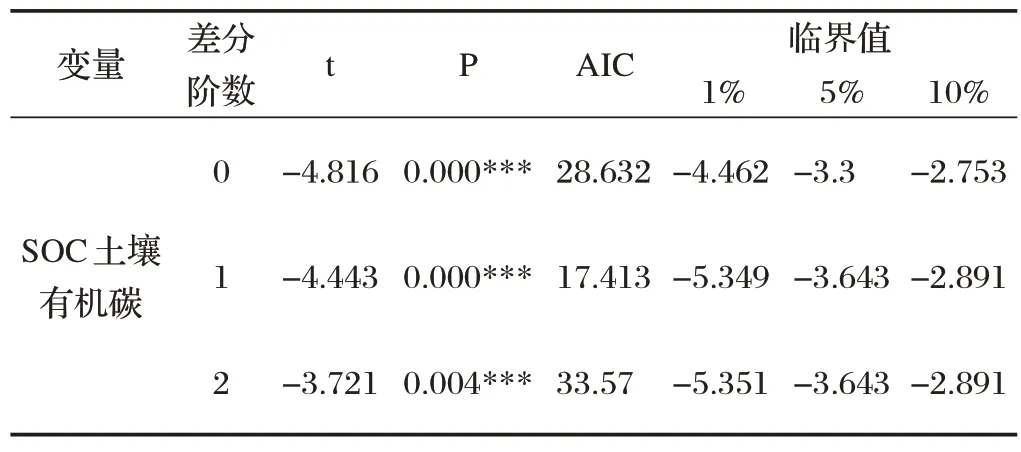
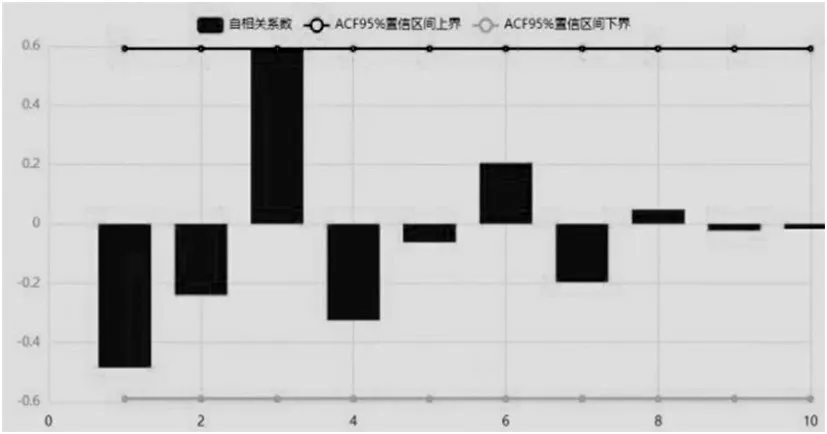
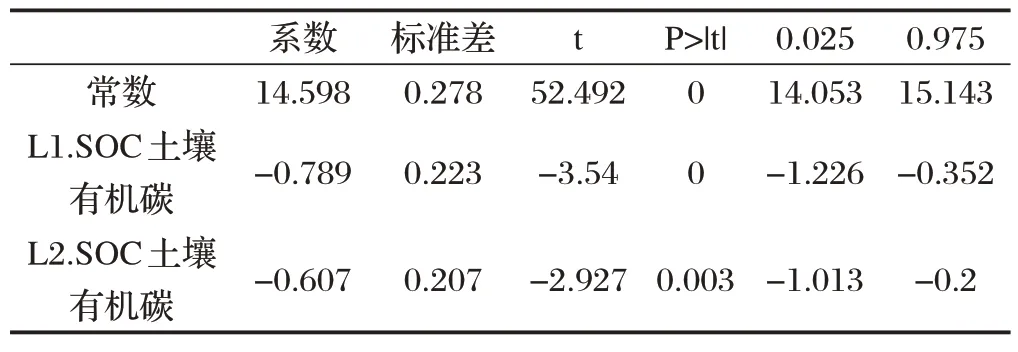
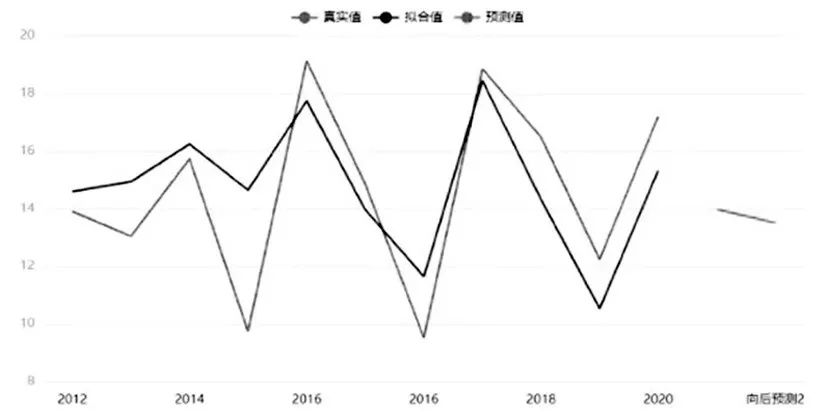
根據表2 可以得到對于SOC 土壤有機碳、SIC 土壤無機碳、STC土壤全碳、全氮N以及土壤C/N 比這五個變量,四種放牧強度的均值大小排序:①對于SOC土壤有機碳,對放牧強度進行排序可以得出:MGI 綜上所述,得出了放牧強度與土地化學性質之間的影響關系,并對其顯著性進行判斷,發現對于STC土壤全碳,HGI 和MGI 存在顯著性差異,其他情況下并不存在顯著性差異。 ARIMA模型全稱是自回歸移動平均模型,是統計模型中一種流行且廣泛使用的時間序列預測統計方法,可記為ARIMA(p,d,q)。 其中AR 是“自回歸”,p代表預測模型中采用的時序數據本身的滯后數(lags);MA為“滑動平均”;q代表預測模型中采用的預測誤差的滯后數(lags) ;d 代表時序數據需要進行幾階差分化[6]。模型的一般形式如式⑼表示: ARIMA時間序列模型的建立主要有以下三個過程: ⑴序列判斷 首先需要對數據進行判斷,確定需要建立的模型數據是否是平穩序列,若P<0.05,則說明時間序列平穩,如果序列不平穩,要對數據做預處理。 ⑵模型估計與建立 當自回歸模型被成功建立后,為了得到最優的模型結構,需要對p 和q 的值進行確定,可以通過自相關系數ACF和偏自相關系數PACF決定。 ⑶模型診斷 對模型參數的顯著性進行判斷,如果模型診斷合格,則可以說明模型設定正確,可以進行最終的預測。 ⑴檢驗ADF 確定模型數據是否是平穩序列,對數據ADF 檢驗,其結果如表3所示。 表3 ADF檢驗表 上表序列檢驗的結果說明,在差分階數是0、1、2階時,該序列是平穩的時間序列,故可進行下一步求解。 ⑵定階 為了確定模型的最優結構,對p 和q 的值進行確定,其中自相關系數ACF 圖與偏自相關系數PACF 圖如圖1、圖2所示。 圖1 自相關系數ACF圖 圖2 偏自相關系數PACF圖 ⑶模型評價與參數確定 將數據帶入模型進行檢驗,結果如表4所示。 表4 ARIMA模型檢驗表 從表4 可得,擬合優度R2為0.724,可知模型表現較好,模型基本滿足要求。 經過模型擬合后的參數如表5所示。 表5 ARIMA模型參數表 以SOC 土壤有機碳為自變量,模型基于AIC 信息準則自動尋找到最優參數后,可建立模型公式如下: 其中,t為預測時間。 ⑷預測結果 根據建立的模型對2022年的數據進行預測,時間序列圖如圖3所示。 圖3 時間序列圖 2022 年預測結果為13.510(結果保留三位有效數字),即在放牧強度為HGI,放牧小區為G9 的條件下,SOC 土壤有機碳含量為13.510。同理,按照上述方法依次對其他數據進行擬合,最終可以得到的預測表,如表6所示。 表6 預測結果 從機理分析的角度,建立放牧策略與草原土壤化學性質關系的數學模型,同時結合數據,采用單因素方差分析模型對放牧策略與草原土壤化學性質關系進行定量分析。發現對于STC 土壤全碳,HGI 和MGI存在顯著性差異,其他情況下并不存在顯著性差異。最后利用ARIMA 模型完成了2022年土壤中化學成分進行預測,預測結果為13.510(結果保留三位有效數字),即在放牧強度為HGI,放牧小區為G9 的條件下,SOC土壤有機碳含量為13.510。其余結果見表6。2 ARIMA時間序列模型的建立
3 結果預測



4 結束語

