常見的類別變量的有調節的中介模型分析*

方 杰 溫忠麟 何子杰

（1.廣東財經大學新發展研究院/應用心理學系，廣州 510320；2.華南師范大學心理學院/心理應用研究中心，廣州 510631；3.廣東財經大學經濟學院，廣州 510320）

有調節的中介模型（moderated mediation model）意味著自變量X 通過中介變量M對因變量Y 產生影響，而中介過程（X→M→Y）受到調節變量Z 的調節（溫忠麟，葉寶娟，2014），圖1（a）是模型概念圖。有調節的中介模型分析既要檢驗中介效應（即X→M→Y 的間接影響）是否受到調節變量Z 的調節，還要檢驗直接效應（即X→Y 的直接影響）是否受到調節變量Z 的調節（圖1（a））。以往的有調節的中介模型研究幾乎都假設X 和Z 是連續變量的情況，但當X或Z 是類別變量（M 和Y 是連續變量），如何進行有調節的中介模型分析呢？如果自變量或調節變量為二分類別變量，可將類別變量進行0 和1 編碼，仍可使用連續變量的有調節的中介模型分析方法進行分析（溫忠麟，劉紅云，2020）。但如果自變量或調節變量為k 個類別（k≥3），問題就變得復雜了。

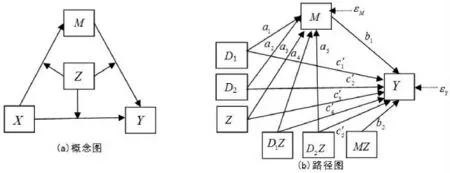
圖1 類別自變量的兩階段被調節的中介模型圖

第一，當自變量是連續變量或二分類別變量時，只有一個中介效應；但當自變量是多類別（k≥3）時，則會有k-1 個相對中介效應（方杰等，2017），也就需要考察k-1個相對中介效應是否被調節（即要檢驗k-1 次），這就增加了問題的復雜性。

第二，有調節的中介模型分為三類，即第一階段（X→M）被調節、第二階段（M→Y）被調節和兩階段被調節的中介模型，需要考察的相對中介效應的數目變為3×（k-1），這進一步增加了問題的復雜性。

第三，有多種方法可以檢驗中介效應是否被調節，溫忠麟等（2014）系統總結了有調節的中介效應的三種檢驗方法，即依次檢驗、系數乘積的區間檢驗和中介效應差異檢驗。那么，當自變量或調節變量為多類別時，在何種情境下應選擇何種檢驗方法更合適呢？

第四，當自變量是多類別（k≥3）時，相對直接效應也從1 個增加為k-1 個（方杰等，2017），如何檢驗k-1 個相對直接效應是否被調節呢？

第五，當調節變量是多類別（k≥3）時，則會有k 個中介效應和k 個直接效應。如何檢驗k 個中介效應是否被調節呢？k 個直接效應是否被調節呢？

這些問題都困擾著應用研究者，直接導致了類別變量的有調節的中介模型分析的實際應用還很少。本文將以三類別的兩階段被調節的中介模型為例，詳述如何正確地進行類別自變量或類別調節變量的有調節的中介模型分析；然后，用一個實例說明如何進行類別變量的有調節的中介模型分析；最后對相關議題做了討論和拓展。

1 類別自變量的兩階段被調節的中介模型分析

三類別自變量（其余變量皆為連續變量）的兩階段被調節的中介模型（見圖1）的分析過程是：

第一，對自變量進行虛擬編碼。由于自變量存在3 個水平，因此研究者可根據研究目的選擇自變量的某個水平為參照水平，產生2 個虛擬變量（D1和D2）（見圖1（b））

第二，兩階段被調節的中介效應分析執行如下回歸方程：

相對參考水平而言，D1→M→Y 的相對中介效應是（a1+a4Z）（b1+b2Z），如果（a1+a4Z）（b1+b2Z）的Bootstrap 置信區間不包含0，表示D1→M→Y 的相對中介效應顯著。調節變量Z 的取值區間內的最大值為Zmax、最小值為Zmin，如果（a1+a4Zmax）（b1+b2Zmax）-（a1+ a4Zmin）（b1+b2Zmin）的Bootstrap 置信區間不包含0，就表示D1→M→Y 的相對中介效應受到Z的調節（溫忠麟，葉寶娟，2014）。相對參考水平而言，D2→M→Y 的相對中介效應是（a2+a5Z）（b1+b2Z），如果（a2+a5Z）（b1+b2Z）的Bootstrap 置信區間不包含0，表示D2→M→Y的相對中介效應顯著。如果（a2+a5Zmax）（b1+b2Zmax）-（a2+a5Zmin）（b1+b2Zmin）的Bootstrap 置信區間不包含0，就表示D2→M→Y 的相對中介效應受到Z 的調節。

同理，相對參考水平而言，D1→Y 的相對直接效應是c1′+c4′Z，如果c1′+c4′Z 的Bootstrap 置信區間不包含0，表示D1→Y的相對直接效應顯著。更進一步，如果相對直接效應之差（c1′+c4′Zmax）-（c1′+c4′Zmin）顯著不等于0，就表示D1→Y 的相對直接效應受到Z 的調節。因為兩個直接效應之差（c1′+c4′Zmax）-（c1′+c4′Zmin）=c4′（Zmax-Zmin），當利用Bootstrap 法獲得c4′（Zmax-Zmin）的置信區間時，Zmax-Zmin在所有Bootstrap 樣本中都為常數，所以c4′的Bootstrap 置信區間不包含0，就表示D1→Y 的相對直接效應受到Z的調節（方杰等，2014）。相對參考水平而言，D2→Y 的相對直接效應是c2′+c5′Z，如果c2′+c5′Z 的Bootstrap 置信區間不包含0，表示D2→Y 的相對直接效應顯著。如果c5′的Bootstrap 置信區間不包含0，表示D2→Y 的相對直接效應受到Z 的調節。如果不考慮直接效應是否被Z 調節，則去掉方程（2）中的c4′D1Z 和c5′D2Z。

2 類別調節變量的兩階段被調節的中介模型分析

三類別調節變量（其余變量皆為連續變量）的兩階段被調節的中介模型（見圖2）的分析過程是：

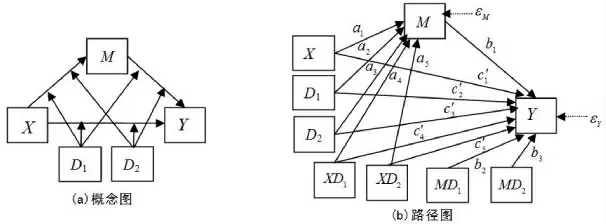
圖2 類別調節變量的兩階段被調節的中介模型圖

第一，對調節變量進行虛擬編碼（見圖2（b）），編碼方法與類別自變量的編碼方法一樣，不再贅述。

第二，兩階段被調節的中介效應分析執行如下回歸方程：

當調節變量Z 為參考水平時（D1=D2=0），中介效應是a1b1，直接效應是c1′。當調節變量Z 為D1時（D1=1 且D2=0），中介效應是（a1+a4）（b1+b2），直接效應是c1′+c4′。當調節變量Z 為D2時（D1=0 且D2=1），中介效應是（a1+a5）（b1+b3），直接效應是c1′+c5′。如果a1b1、（a1+a4）（b1+b2）、（a1+a5）（b1+b3）的Bootstrap 置信區間不包含0，則表示中介效應顯著。如果c1′、c1′+c4′、c1′+c5′的Bootstrap置信區間不包含0，則表示直接效應顯著。

調節變量Z 為D1和參考水平的中介效應之差為（a1+a4）（b1+b2）-a1b1=a1b2+a4b1+a4b2，如果a1b2+a4b1+a4b2的Bootstrap 置信區間不包含0，則表示中介效應受到Z 的調節。調節變量Z 為D2和參考水平的中介效應之差為（a1+a5）（b1+b3）-a1b1=a1b3+a5b1+a5b3，如果a1b3+a5b1+a5b3的Bootstrap 置信區間不包含0，則表示中介效應受到Z 的調節。

調節變量Z 為D1和參考水平的直接效應之差為（c1′+c4′）-c1′=c4′，如果c4′的Bootstrap 置信區間不包含0，則表示直接效應受到Z 的調節。調節變量Z 為D2和參考水平的直接效應之差為（c1′+c5′）-c1′=c5′，如果c5′的Bootstrap 置信區間不包含0，則表示直接效應受到Z 的調節。如果不考慮直接效應是否被Z 調節，則去掉方程（4）中的c4′XD1和c5′XD2。

3 示 例

接下來用一個例子演示如何進行類別變量的有調節的中介模型分析。本例感興趣的是，公正感（X）通過負性情緒（M）影響員工偏離行為（Y）的中介過程，是否受到了性別（Z）的調節，模型如圖1 所示。本例的所有變量及其數據均來自方杰等（2017）。自變量公正感是類別變量（分為低、中、高三水平），采用虛擬編碼，產生2 個虛擬變量（D1和D2）。低公正感為參照水平，編碼為D1=0 和D2=0；中等公正感編碼為D1=1和D2=0；高公正感編碼為D1=0 和D2=1。中介變量負性情緒和因變量員工偏離行為是連續變量，調節變量為性別（0 表示女，1 表示男）。我們使用SPSS 軟件運行PROCESS 3.4的模型59（PROCESS 還可在SAS 和R軟件上運行），進行兩階段被調節的中介模型分析。分析結果如表1 所示。模型1 對應方程（1），模型2 對應方程（2）。具體分析如下：

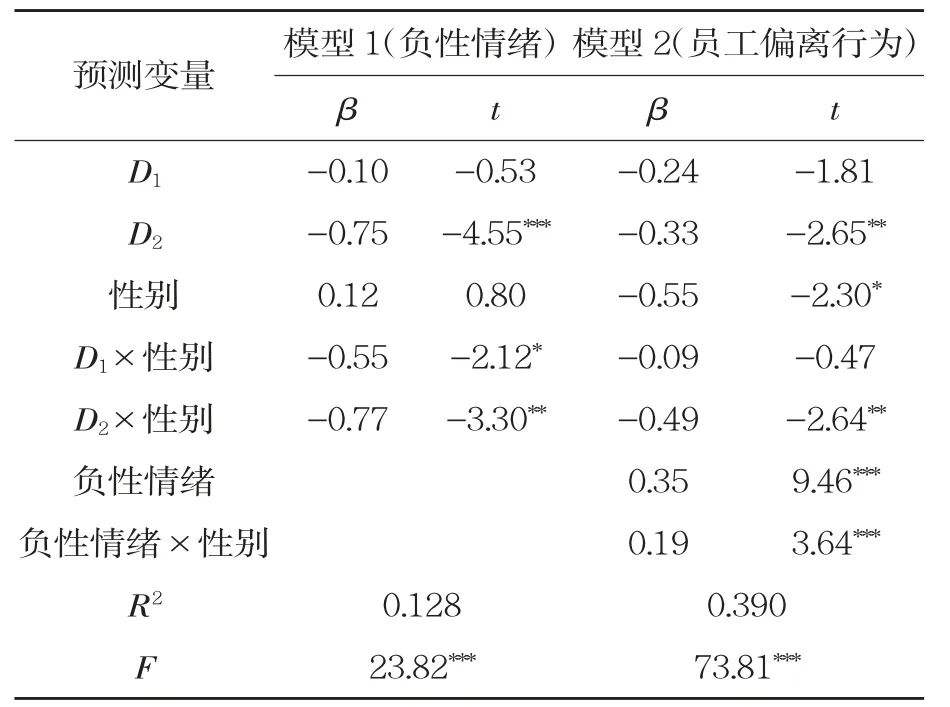
表1 三類別自變量的兩階段被調節的中介效應分析結果

3.1 有調節的中介效應分析

在性別為女（Z=0）時，相對于低公正感，中等公正感的相對中介效應a1b1為-0.033，SE=0.061，95%的 非 參 數 百 分 位Bootstrap 法的置信區間［-0.154，0.085］，包含0，相對中介效應不顯著。在性別為男（Z=1）時，相對于低公正感，中等公正感的相對中介效應（a1+a4）（b1+b2） 為-0.346，SE=0.106，95%的非參數百分位Bootstrap法的置信區間［-0.559，-0.145］，不包含0，相對中介效應顯著。男女中介效應的差（a1+a4）（b1+b2）-a1b1=a1b2+a4b1+a4b2=-0.313，SE=0.120，95%的非參數百分位Bootstrap法的置信區間［-0.554，-0.079］，不包含0，由此得出結論，相對于低公正感，中等公正感的相對中介效應受到性別的調節。

在性別為女（Z=0）時，相對于低公正感，高公正感的相對中介效應a2b1為-0.262，SE=0.071，95%的 非 參 數 百 分 位Bootstrap 法的置信區間［-0.413，-0.134］，不包含0，相對中介效應顯著。在性別為男（Z=1）時，相對于低公正感，高公正感的相對中介效應（a2+a5）（b1+b2）為-0.823，SE=0.108，95%的非參數百分位Bootstrap 法的置信區間［-1.045，-0.619］，不包含0，相對中介效應顯著。男女中介效應的差（a2+a5）（b1+b2）-a2b1= a2b2+a5b1+a5b2= -0.561，SE=0.128，95%的非參數百分位Bootstrap法的置信區間［-0.811，-0.311］，不包含0，由此得出結論，相對于低公正感，高公正感的相對中介效應受到性別的調節。

3.2 有調節的直接效應分析

在性別為女（Z=0）時，相對于低公正感，中等公正感的相對直接效應c1′為-0.24，SE=0.134，95% 的 非 參 數 百 分 位Bootstrap 法的置信區間［-0.504，0.021］，包含0，相對直接效應不顯著。在性別為男（Z=1）時，相對于低公正感，中等公正感的相對直接效應c1′+c4′為-0.33，SE= 0.139，95%的非參數百分位Bootstrap 法的置信區間［-0.605，-0.059］，不包含0，相對直接效應顯著。男女直接效應的差c4′為-0.09，SE=0.193，95%的非參數百分位Bootstrap法的置信區間［-0.469，0.289］，包含0，表明相對于低公正感，中等公正感的相對直接效應沒有受到性別的調節。

在性別為女（Z=0）時，相對于低公正感，高公正感的相對直接效應c2′為-0.33，SE=0.126，95%的非參數百分位Bootstrap法的置信區間［-0.581，-0.086］，不包含0，相對直接效應顯著。在性別為男（Z=1）時，相對于低公正感，高公正感的相對直接效應c2′+c5′為-0.83，SE=0.136，95%的非參數百分位Bootstrap 法的置信區間［-1.090，-0.556］，不包含0，相對直接效應顯著。男女直接效應的差c5′為-0.49，SE=0.185，95%的非參數百分位Bootstrap 法的置信區間［-0.853，-0.126］，不包含0，表明相對于低公正感，高公正感的相對直接效應受到性別的調節。

需要說明的是，雖然示例使用了PROCESS 插件進行數據分析，實際上還可以使用Mplus 軟件對示例數據進行類別變量的有調節的中介效應分析。具體地，先將示例數據的三類別自變量進行虛擬變量編碼，產生D1和D2兩個新變量，然后利用Mplus 程序（見圖3）進行有調節的中介模型分析，分析結果與PROCESS 的分析結果一致，不再贅述。

圖3 類別自變量的兩階段被調節的中介模型分析的Mplus 程序

4 討論與拓展

類別變量在心理學和其他社科領域研究中經常遇到，已有文獻討論了類別變量的中介和調節分析方法（方杰等，2017；方杰，溫忠麟，2022），但如果將中介和調節整合在一起，進行類別變量的有調節的中介模型分析，問題就變得復雜了。本文試圖為應用研究者提供相應的方法學支持。在闡述了類別變量的兩階段被調節的中介模型的分析方法后，用示例演示如何進行分析。但是，本文介紹的方法尚有不足，有待進一步研究和拓展。

4.1 模型拓展

本文只涉及兩階段被調節的中介模型，實際上本文的步驟和方法同樣適用于第一階段（X→M）、第二階段（M→Y）被調節的中介模型和有中介的調節模型。

4.1.1 第一階段被調節的中介模型

如果是類別自變量的第一階段被調節的中介模型，只需要方程（2）去掉b2MZ 即可。相對參考水平而言，D1→M→Y 的相對中介效應變為（a1+a4Z）b1，如果a4b1的Bootstrap 置信區間不包含0，就表示D1→M→Y 的相對中介效應受到Z 的調節。相對參考水平而言，D2→M→Y 的相對中介效應變為（a2+a5Z）b1，如果a5b1的Bootstrap 置信區間不包含0，就表示D2→M→Y 的相對中介效應受到Z 的調節。相對參考水平而言，如果c4′或（和）c5′的Bootstrap 置信區間不包括0，就表示D1→Y 或（和）D2→Y 的相對直接效應受到Z 的調節（Hayes，2018）。

如果是類別調節變量的第一階段被調節的中介模型，只需要方程（4）去掉b2MD1和b3MD2即可。此時，調節變量Z 為D1時的中介效應變為（a1+a4）b1，Z 為D2時的中介效應變為（a1+a5）b1，如果a4b1或a5b1的Bootstrap 置信區間不包含0，則表示中介效應受到Z 的調節，如果c4′或c5′的Bootstrap置信區間不包含0，則表示直接效應受到Z的調節。

4.1.2 第二階段被調節的中介模型

如果是類別自變量的第二階段被調節的中介模型，只需要方程（1）去掉a3Z、a4D1Z和a5D2Z 即可。相對參考水平而言，D1→M→Y 的相對中介效應變為a1（b1+b2Z），如果a1b2的Bootstrap 置信區間不包含0，就表示D1→M→Y 的相對中介效應受到Z 的調節。相對參考水平而言，D2→M→Y 的相對中介效應變為a2（b1+b2Z），如果a2b2的Bootstrap 置信區間不包含0，就表示D2→M→Y 的相對中介效應受到Z 的調節。相對參考水平而言，如果c4′或（和）c5′的Bootstrap 置信區間不包括0，就表示D1→Y或（和）D2→Y 的相對直接效應受到Z 的調節。

如果是類別調節變量的第二階段被調節的中介模型，只需要方程（3）去掉a2D1、a3D2、a4XD1和a5XD2即可。此時，調節變量Z為D1時的中介效應變為a1（b1+b2），Z 為D2時的中介效應變為a1（b1+b3），如果a1b2或a1b3的Bootstrap 置信區間不包含0，則表示中介效應受到Z 的調節，如果c4′或c5′的Bootstrap 置信區間不包含0，則表示直接效應受到Z 的調節。

4.1.3 有中介的調節模型

本文只涉及有調節的中介模型。實際上還有一種中介和調節的整合模型，即有中介的調節模型。有中介的調節模型可分為兩種，一種是有中介的調節模型Ι，即調節變量Z 調節自變量X 和因變量Y 的關系，而這種調節效應至少部分地通過中介變量M 對Y 起作用。有中介的調節模型Ι 的分析步驟與第一階段被調節的中介模型的分析步驟一致（Edwards & Lambert，2007；溫忠麟等，2022；王陽等，2022）。另一種是有中介的調節模型Ⅱ，即Z 先影響M，再由M 調節X 和Y 的關系。有中介的調節模型Ⅱ的分析步驟與第二階段被調節的中介模型（需將Z 當成自變量、X 當成調節變量）的分析步驟一致（Kwan & Chan，2018；溫忠麟等，2022；王陽等，2022）。因此，類別變量的有調節的中介模型的分析步驟和方法可以方便地推廣到類別變量的有中介的調節模型分析中。

4.2 變量的拓展

本文的有調節的中介模型都假設因變量是連續變量，實際上本文的步驟和方法都可以拓展到因變量是二分類別變量的情況。具體地，方程（1）和（3）仍然使用多元線性回歸，但方程（2）和（4）使用Logistic 回歸代替多元線性回歸即可。PROCESS 4.0 可以方便地執行二分因變量的有調節的中介效應分析，因此PROCESS 4.0 可分析2（多類別/連續自變量）×2（多類別/連續調節變量）×2（二分類別/連續因變量）×3（調節的中介路徑類型）共24 種類別變量的有調節的中介模型。值得注意的是，PROCESS 4.0 在進行二分因變量的有調節的中介效應分析時，直接將系數a 和b 相乘得到中介效應大小，使得中介效應存在量尺不統一的問題，即X→M 的影響a 是連續變量的量尺，M→Y 的影響b 是Logit量尺。已有研究者在二分因變量的簡單中介模型的分析中，提出了兩種統一量尺的方法（方杰等，2017；劉紅云等，2013）。一種方法是將系數b 標準化為bstd（MacKinnon& Dwyer，1993），對a×bstd進行顯著性檢驗；另一種方法是將系數a 和b 各自變為Za=a／SE(a)和Zb=b／SE(b)，再對Za×Zb進行顯著性檢驗（Iacobucci，2012）。這兩種方法是否適用于二分因變量的有調節的中介模型，還有待進一步深入研究。

同理，本文的有調節的中介模型也可以推廣到中介變量是二分類別變量的情況。具體地，方程（2）和（4）仍然使用多元線性回歸，但方程（1）和（3）使用Logistic 回歸代替多元線性回歸即可，此時也存在量尺不統一的問題。PROCESS 4.0 暫時無法執行二分中介變量的有調節的中介模型分析，此時建議使用SPSS 軟件分別執行多元線性回歸和Logistic 回歸，得到各個系數值及其顯著性檢驗結果，再判斷中介效應是否受到調節（溫忠麟，葉寶娟，2014；溫忠麟，劉紅云，2020）。如果因變量和中介變量都是二分類別變量，則方程（1）~（4）都用Logistic 回歸代替多元線性回歸，此時量尺是統一的，建議用SPSS 軟件執行Logistic回歸，得到各個系數值及其顯著性檢驗結果，再判斷中介效應是否受到調節。

4.3 類別變量的編碼方式的拓展

本文僅用虛擬編碼［又稱為指標編碼（indicator code）］對多類別變量進行編碼，實際上PROCESS 還提供了另外三種編碼方式供研究者選用，即序列編碼（sequential code）、效應編碼（effect code）和Helmet 編碼（見表2）。所有的編碼方式都可使用相同的有調節的中介模型的分析步驟和方法。

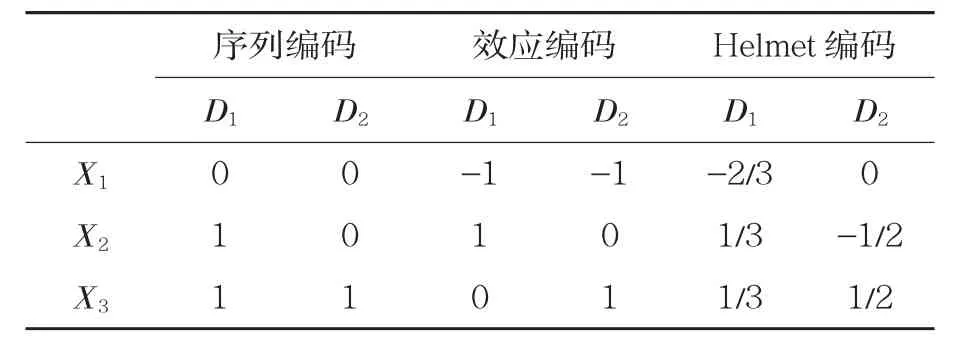
表2 三類別變量的各種編碼方式

如果研究者感興趣的是X1和X2之間的對比以及X1和X3之間的對比，則建議使用虛擬編碼。如果研究者感興趣的是X1和X2之間的對比以及X2和X3之間的對比，則建議使用序列編碼。使用示例數據，用序列編碼進行兩階段被調節的中介模型分析，結果還發現相對于中等公正感，高公正感的相對中介效應不受性別的調節。

如果自變量是有序類別變量（ordinal categorical variable），則在下述情況下推薦使用Helmet 編碼。例如，自變量是新冠疫情下的自我保護程度，包括三個水平：不保護，少量保護（只有自己戴口罩，其他人不戴口罩）和充分保護（全社區人員都戴口罩），保護程度是有序增強，此時推薦使用Helmet 編碼。因為此時研究者或許感興趣的是不保護X1和有保護（X2和X3）之間的對比以及少量保護X2和充分保護X3之間的對比（Hayes，2018）。如果研究者感興趣的是X2和（X1和X3）之間的對比以及X3和（X1和X2）之間的對比，則建議使用效應編碼。因此，建議研究者在闡述結果前，先說明類別變量的編碼方式。

5 結 語

目前，類別變量的有調節的中介模型的實際應用還較少，一個較為重要的原因是，應用研究者還不清楚如何正確地進行類別變量的有調節的中介模型分析。表3將常用的類別變量的有調節的中介模型及其分析策略進行了總結，便于應用研究者了解哪些場景或模型應該使用類別變量的有調節的中介模型進行數據分析，并能按圖索驥地選擇合適的分析策略。

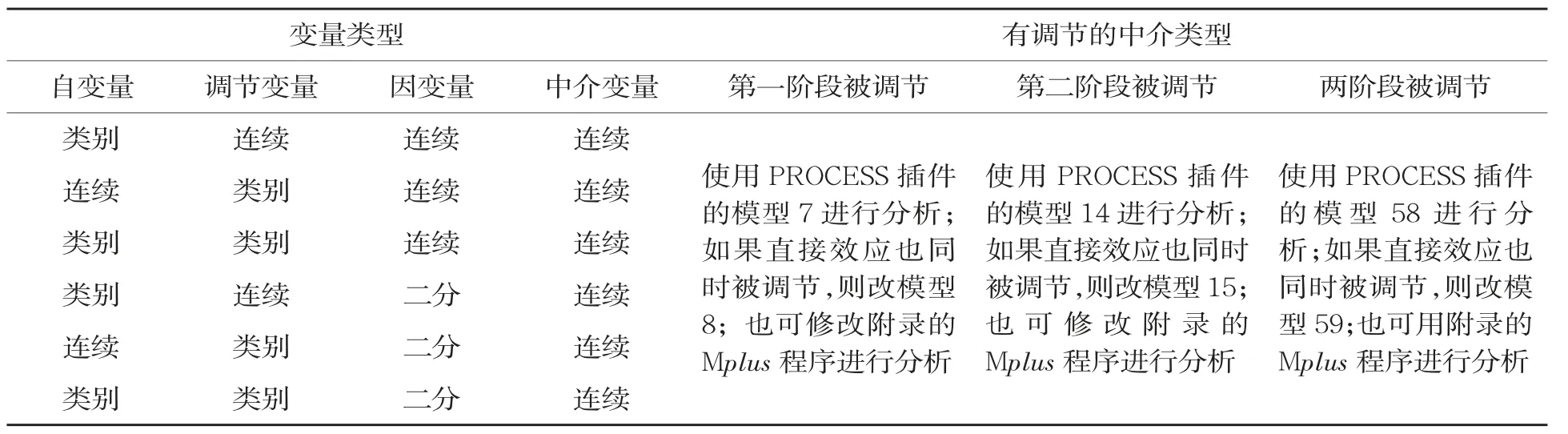
表3 常見的類別變量的有調節的中介模型及其分析策略

另外，雖然本文是以三類別的類別變量為例進行闡述，但本文的方法同樣也適用于4 個類別或更多類別的情況，如果自變量是n 個類別，就產生n-1 個虛擬變量（D1、D2、…、Dn-1）和n-1 個相對中介效應，需要檢驗n-1 個相對中介效應各自是否被調節。同理，還需要檢驗n-1 個相對直接效應各自是否被調節。如果是五個或五個以上類別的類別變量，實際上可當成連續變量處理（溫忠麟，劉紅云，2020）。

現在，類別變量的有調節的中介模型分析的方法學研究還處于蓬勃發展階段，還有諸多問題亟待解決。例如，在多層嵌套數據中，如何進行類別變量的有調節的多層中介模型分析呢？再如，本文僅涉及一個中介變量，如果模型中存在多個中介變量，如何進行類別變量的有調節的多重中介模型分析呢？又如，本文僅涉及因變量或中介變量是二分類別變量的情況，如果因變量或中介變量為多類別變量，如何進行有調節的中介模型分析？相信隨著方法研究的深入，會不斷增加我們對類別變量的有調節的中介問題的理解。