基于問題為主線的探究式教學

孫強　章建榮

一元線性回歸模型是高中數(shù)學的一個統(tǒng)計學模型，而“相關(guān)系數(shù)”是一元線性回歸模型中判斷線性相關(guān)性的一個重要的統(tǒng)計量，其產(chǎn)生過程蘊含著統(tǒng)計學探究的一般思維方式，推導過程中的類比、特殊化等數(shù)學思想方法，是培養(yǎng)學生統(tǒng)計學思維、符號運算能力、邏輯推理能力及數(shù)據(jù)處理思維等素養(yǎng)的落地點.然而，很多教學課在統(tǒng)計量的出現(xiàn)以及公式推導探究過程中并沒有很好地體現(xiàn)出“相關(guān)系數(shù)”這一統(tǒng)計量的必要性以及公式的生成過程，讓學生的數(shù)學思維得不到良好的發(fā)展，難以體現(xiàn)和落實核心素養(yǎng).基于這些問題，筆者開展了相關(guān)的教學設(shè)計和教學實踐.旨在通過“相關(guān)系數(shù)”這一統(tǒng)計學概念的教學，探究其在教學過程中自然生成，同時以問題探究為主線，引導學生思考和探索“相關(guān)系數(shù)”的計算公式，幫助學生體會統(tǒng)計學的探究過程，感悟其中的數(shù)學思想，從而營造高效的數(shù)學課堂.

一、教學內(nèi)容分析

“相關(guān)系數(shù)”是北師大版《普通高中教科書·數(shù)學（選擇性必修一）》第七章“統(tǒng)計案例”第二節(jié)的內(nèi)容，它既是之前一元線性回歸的延續(xù)，也是學生學習的第一個統(tǒng)計學模型，對今后的統(tǒng)計學學習具有指導意義.《普通高中數(shù)學課程標準（2017年版）》的要求是：①結(jié)合實例，了解樣本相關(guān)系數(shù)的統(tǒng)計含義，了解樣本相關(guān)系數(shù)與標準化數(shù)據(jù)向量夾角的關(guān)系.②結(jié)合實例，會通過相關(guān)系數(shù)比較多組成對數(shù)據(jù)的相關(guān)性.因此，本節(jié)課的主要任務是了解樣本相關(guān)系數(shù)這一概念為什么會出現(xiàn)，為什么需要相關(guān)系數(shù)這一統(tǒng)計量，如何研究一個統(tǒng)計模型；其次是如何定義和計算樣本相關(guān)系數(shù).

二、學情分析

學生已經(jīng)學過一元線性回歸方程，對成對數(shù)據(jù)的一元線性擬合有了基本的了解.也會利用散點圖來觀察成對數(shù)據(jù)是否相關(guān)，但是這種對于相關(guān)的感知僅僅停留在直觀的認知上，而并非在科學意義上的嚴格計算，對于許多成對數(shù)據(jù)是否相關(guān)，相關(guān)性有多大，還沒有一個明確的概念.因此本節(jié)課應該從學生已有相關(guān)性的經(jīng)驗出發(fā)，給出直觀觀察解決不了的問題，讓學生感知到相關(guān)系數(shù)出現(xiàn)的必要性，從而引出沖突，讓概念自然生成.

三、教學過程

1.創(chuàng)設(shè)情景，引導思考

問題1 給定兩個隨機變量（x，y）的7組成對數(shù)據(jù)：（1，0），（4/5，3/5），（0，1），（－4/5，3/5），（－1，0），（－4/5，－3/5），（0，－1），利用最小二乘法，可以得到Y(jié)關(guān)于X的線性回歸方程Y=0.143X+0.102.這時，X和Y是否具有線性關(guān)系呢？

教師畫出散點圖，讓學生進行觀察，學生容易發(fā)現(xiàn)7組成對數(shù)據(jù)均位于單位圓上，所以X和Y不具備線性關(guān)系，用這一組數(shù)據(jù)建立的線性回歸方程無法精確刻畫這組數(shù)據(jù).

師：對一組數(shù)據(jù)進行直線擬合之前先應該做什么？

生：先要判斷這組數(shù)據(jù)是否適合進行直線擬合.

師：應該如何進行判斷？

生：可以畫出散點圖直接看所有的點是不是大概在一條直線上.

師：對了，對于數(shù)據(jù)量較小且散點圖較規(guī)則的數(shù)據(jù)確實可以畫散點圖來進行觀察判斷，那不妨看看的散點圖1及圖2，這個散點圖是否適合直線擬合？那如果再多幾個樣本點呢？這樣是否適合呢？

師生互相討論后得出要引入一個統(tǒng)計量來定量的刻畫樣本數(shù)據(jù)的線性相關(guān)程度.

設(shè)計意圖：引導學生分析一組數(shù)據(jù)是否能進行直線擬合不能僅僅通過肉眼觀察，而是需要一個統(tǒng)計量來定量刻畫線性相關(guān)程度的強弱，進而引出本節(jié)課的研究目標.讓學生初步感受構(gòu)建一個統(tǒng)計量的必要性，從定性向定量過渡，從而自然引出相關(guān)系數(shù).

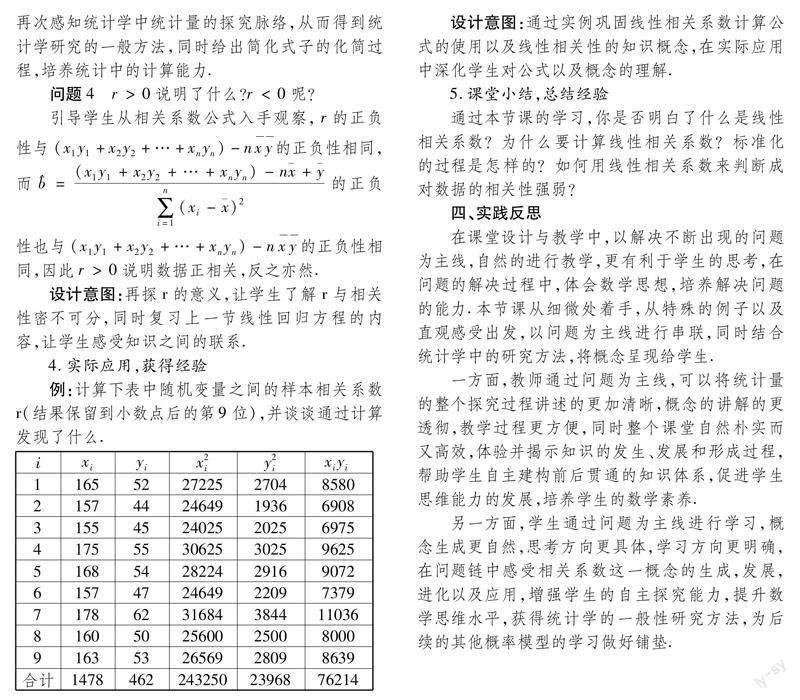
設(shè)計意圖：通過實例鞏固線性相關(guān)系數(shù)計算公式的使用以及線性相關(guān)性的知識概念，在實際應用中深化學生對公式以及概念的理解.

5.課堂小結(jié)，總結(jié)經(jīng)驗

通過本節(jié)課的學習，你是否明白了什么是線性相關(guān)系數(shù)？為什么要計算線性相關(guān)系數(shù)？標準化的過程是怎樣的？如何用線性相關(guān)系數(shù)來判斷成對數(shù)據(jù)的相關(guān)性強弱？

四、實踐反思

在課堂設(shè)計與教學中，以解決不斷出現(xiàn)的問題為主線，自然的進行教學，更有利于學生的思考，在問題的解決過程中，體會數(shù)學思想，培養(yǎng)解決問題的能力.本節(jié)課從細微處著手，從特殊的例子以及直觀感受出發(fā)，以問題為主線進行串聯(lián)，同時結(jié)合統(tǒng)計學中的研究方法，將概念呈現(xiàn)給學生.

一方面，教師通過問題為主線，可以將統(tǒng)計量的整個探究過程講述的更加清晰，概念的講解的更透徹，教學過程更方便，同時整個課堂自然樸實而又高效，體驗并揭示知識的發(fā)生、發(fā)展和形成過程，幫助學生自主建構(gòu)前后貫通的知識體系，促進學生思維能力的發(fā)展，培養(yǎng)學生的數(shù)學素養(yǎng).

另一方面，學生通過問題為主線進行學習，概念生成更自然，思考方向更具體，學習方向更明確，在問題鏈中感受相關(guān)系數(shù)這一概念的生成，發(fā)展，進化以及應用，增強學生的自主探究能力，提升數(shù)學思維水平，獲得統(tǒng)計學的一般性研究方法，為后續(xù)的其他概率模型的學習做好鋪墊.

本文系江西省教育科學 “十四五”規(guī)劃2022年度課題《高中數(shù)學“一課四研”教研范式的研究》（編號：22PTZD035）的研究成果.