連續剛構橋地震響應時程分析及荷載譜研究

黃曉東

(中國華西工程設計建設有限公司,四川 成都 610000)

0 引言

在社會不斷發展的時代背景下,橋梁結構的設計理念已逐漸往個性化發展,對橋梁結構的抗震設計要求也逐步提升,在抗震設計中,尤其是針對連續鋼構橋具有在支座處采用剛性連接的特點,剛性結構受地震的影響較大,在抗震設計時,應密切關注可能出現的橋梁結構的失衡與振動破壞的影響,在設計階段應嚴格把控橋梁的抗震設計要求,把握抗震對連續鋼構橋的影響程度。因此,對連續剛構橋進行抗震分析十分有必要。

大量學者對橋梁的抗震性能進行了大量研究。高金亮[1]基于關防大橋案例,獲得了地震作用下,橋梁結構的塑性變形變化時程,以此指導設計人員進行合理設計;朱清華[2]采用有限元軟件,構建了基于抗震要求的連續剛構橋計算模型,獲得了橋墩薄弱截面的塑性變形區域;曾輝[3]基于橋梁結構、地震位移等病害,提出新的抗震設計方法,優化橋梁下部結構的加固方案;陳奕涵[4]考慮了連續剛構橋近斷層圖紙的影響,對高速鐵路地震速度脈沖進行響應分析,提出黏滯流體阻尼器的減震原則;張鵬[5]采用擬靜力非線性分析方法,對基于位移的橋梁抗震提出新的迭代計算設計方法;張劍峰等[6]基于高烈度抗震地區,采用不同波形,對鋼-混凝土組合橋梁進行地震響應分析,獲得橋梁結構的位移與內力分布最不利位置。

文獻研究結果表明,橋梁抗震規律分析及處置方法受到廣大學者的關注。由于剛構橋本身剛性結構的特殊性,本文依托于某大橋的結構特點,采用EI-Centro地震波分析連續剛構橋的時程及頻譜與荷載的關系,獲得連續鋼構橋的地震響應規律,為設計前期提供理論指導。

1 EI-Centro波與時程分析理論

1.1 EI-Centro地震波

隨著地震波監控系統的不斷完善,近年來,包括天津波、塔夫特波、埃爾森特羅波(EI-Centro)等,其中,埃爾森特羅波(EI-Centro)最典型,于1940年記錄。依據近年來記錄的地震波特點,采用典型波EI-Centro進行地震分析連續鋼構橋的響應規律,EI-Centro波的真實記錄時間為53.73 s,在2.22 s出現波峰值為0.28g,在2.14 s出現波谷值為-0.36g(見圖1),由于地震加速度值在前30 s內響應較大,因此,本文在計算時采取前30 s進行分析。

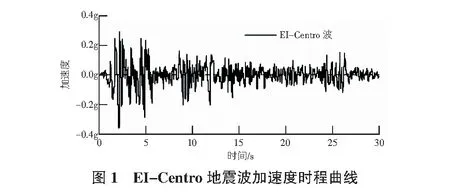
1.2 時程分析理論

時程分析理論在20世紀60年代初逐步得到發展,該理論最早應用于高聳建筑物的抗震分析,隨后在大跨度橋梁逐漸獲得應用,由于時程分析法理論是基于地震波的時間、加速度,以此獲得結構內部的內力值隨時間的變化,該理論與反應譜法相比具有體現直觀內力變化的優點。時程分析理論的計算模型是基于結構振動方程,采用微分法結合已記錄的地震波進行求解積分的過程,最終解出對應時間節點的響應狀態[7]。

直接積分法是時程分析法最直接的求解方式,時程一般包括彈塑性時程與彈性時程兩方面,由于求解方程的復雜程度較高,運算體量較大,采用有限元軟件進行分析能夠得到很大幫助。具體步驟如下所示:

1)將地震波響應時程的記錄數據以試件為基準進行劃分,用Δt表示,其中,Δt可以選用相等間隔時間或者不等間隔時間均可。

2)時間間隔Δt內的反映物理量值應按照特指的規律性進行劃分,然后依據規律性的不同采用不同的算法求解,常用的求解方法如Newmark-β和Wilson-θ、線性加速度法等。

3)求解某時刻t+Δt的結構物理量值應滿足如下動力平衡關系:

[kD]{Δa}t+Δt={ΔFD}

(1)

其中,[kD]為動力等效剛度矩陣;{ΔFD}為動力等效荷載向量。

4)將上述步驟進行重復求解,直至最終的地震波響應時程全部完成。

2 有限元模型建立

2.1 數值模型

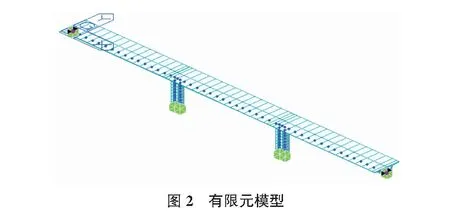
采用有限元軟件,建立連續剛構橋的有限元模型。全橋由3主跨與2橋墩組成,全長為120 m,其中,左、中、右三跨均為40 m,橋墩高度為10 m。有限元模型共有99個節點,98個單元,組合結構采用梁單元,兩邊跨設置Dy,Dz,Rx,Rz約束,墩底和墩頂支座采用剛性連接,全橋的有限元模型如圖2所示。連續剛構橋的橫斷面如圖3所示。

2.2 計算參數

連續剛構橋的模型計算參數如表1,表2所示。

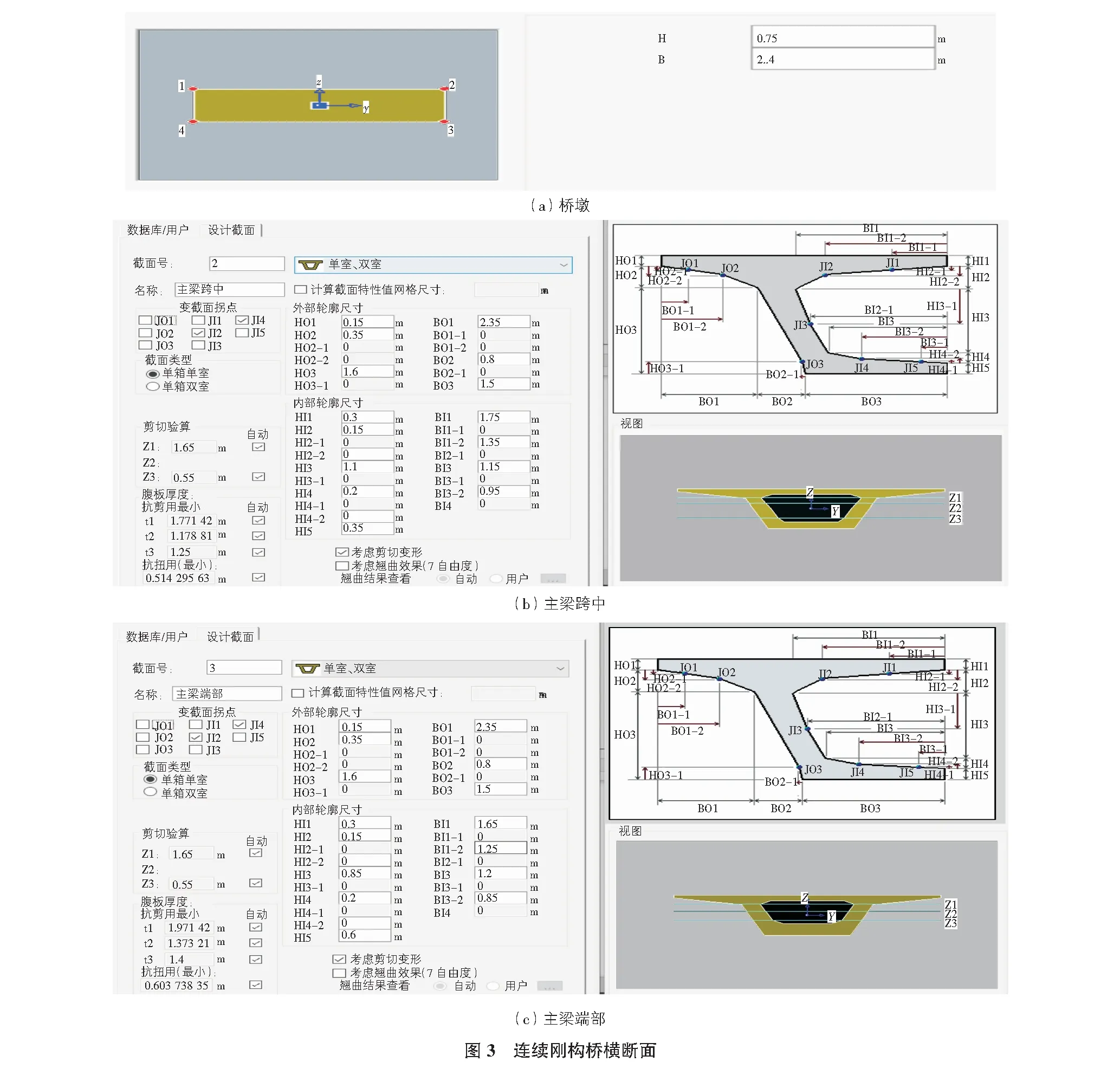
表1 混凝土力學參數

表2 鋼絞線力學參數

3 連續剛構橋地震響應分析

3.1 荷載-時程曲線結果

墩底、墩頂、支座、橋梁邊跨跨中及橋梁中跨跨中的荷載-時程曲線見圖4,最大彎矩與時間關系見表3。

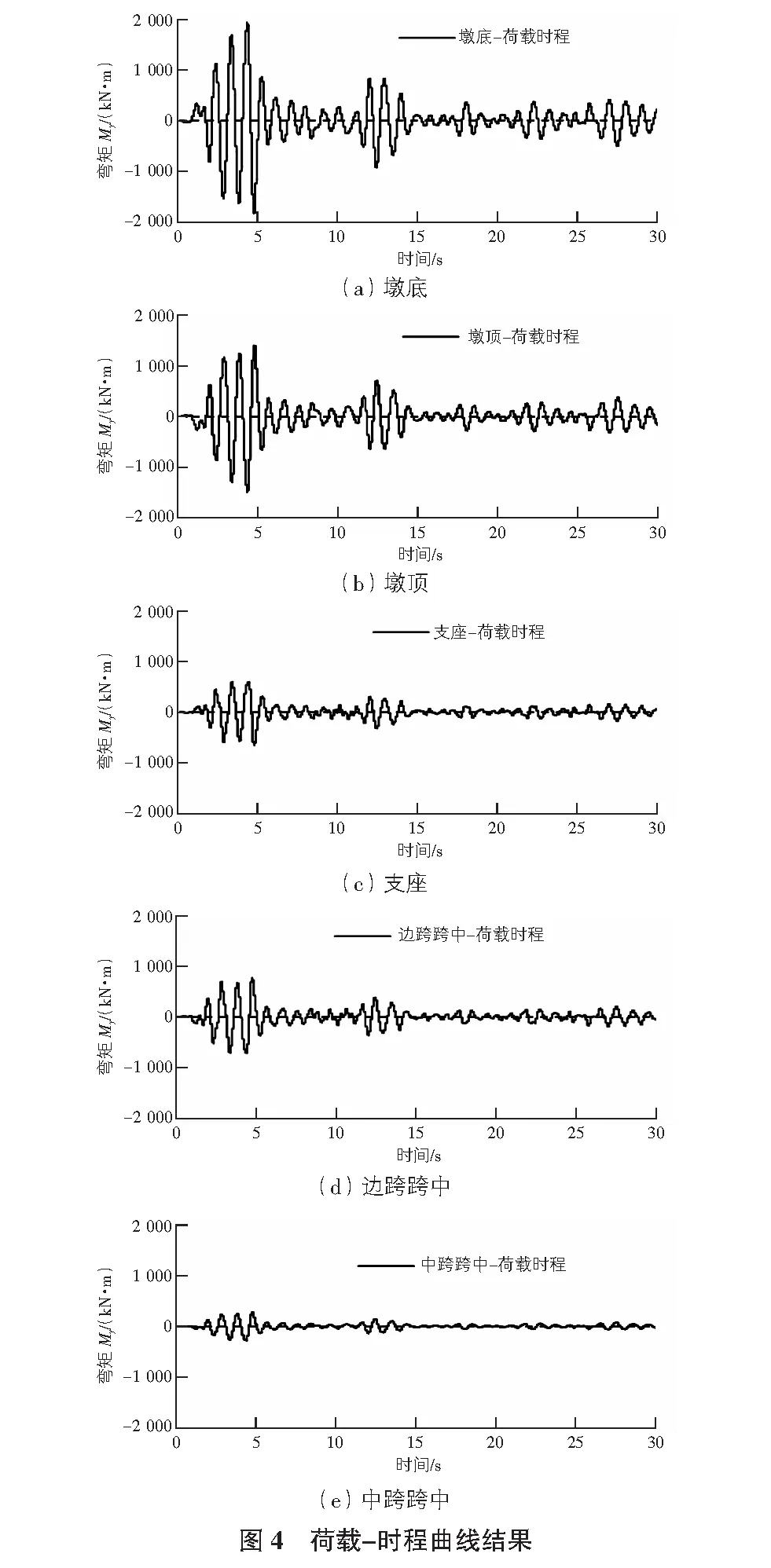
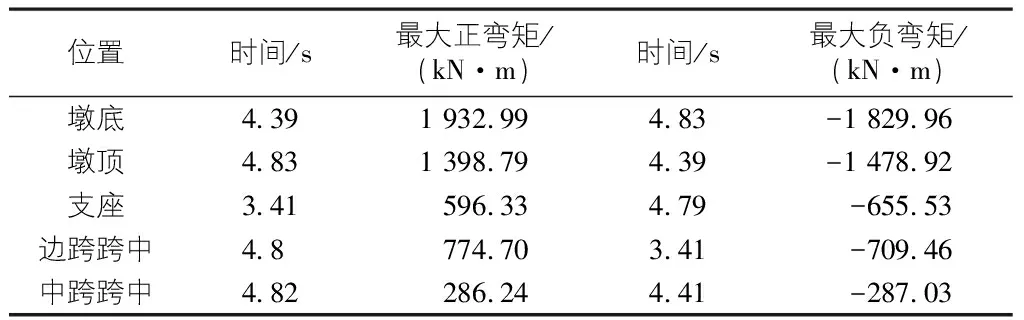
表3 最大彎矩與時間關系表

由圖4可知,隨著EI-Centro地震波的輸入,連續剛構橋的彎矩值具有隨時間呈現周期性變化的規律,與EI-Centro地震波圖像具有一致現象,隨著地震荷載從墩底、墩頂、支座、邊跨跨中、中跨跨中不斷向上傳遞,彎矩值逐漸衰減,由于該結構具有對稱性,下部結構由兩個橋墩組成,在中跨跨中的彎矩值受到兩橋墩地震波振動的相互影響,彎矩值減小量較大,最大正彎矩僅為286.24 kN·m,最大負彎矩僅為-287.03 kN·m。

由表3可知,從橋墩上看,在時間達到4.39 s時,墩底達到最大正彎矩值為1 932.99 kN·m,墩頂達到最大負彎矩值-1 478.92 kN·m,在時間達到4.83 s時,墩底達到最大負彎矩值為-1 829.96 kN·m,墩頂達到最大正彎矩值1 398.79 kN·m,可見墩底與墩頂值在同一時間內具有反方向運動的趨勢;從主梁上看,邊跨跨中彎矩相比于支座處的彎矩稍微增大,中跨跨中彎矩相比于支座處的彎矩減小較為明顯。

3.2 荷載-頻譜曲線結果

墩底、墩頂、支座、橋梁邊跨跨中及橋梁中跨中的最大動彎矩與頻率關系見表4,荷載-頻譜曲線見圖5。

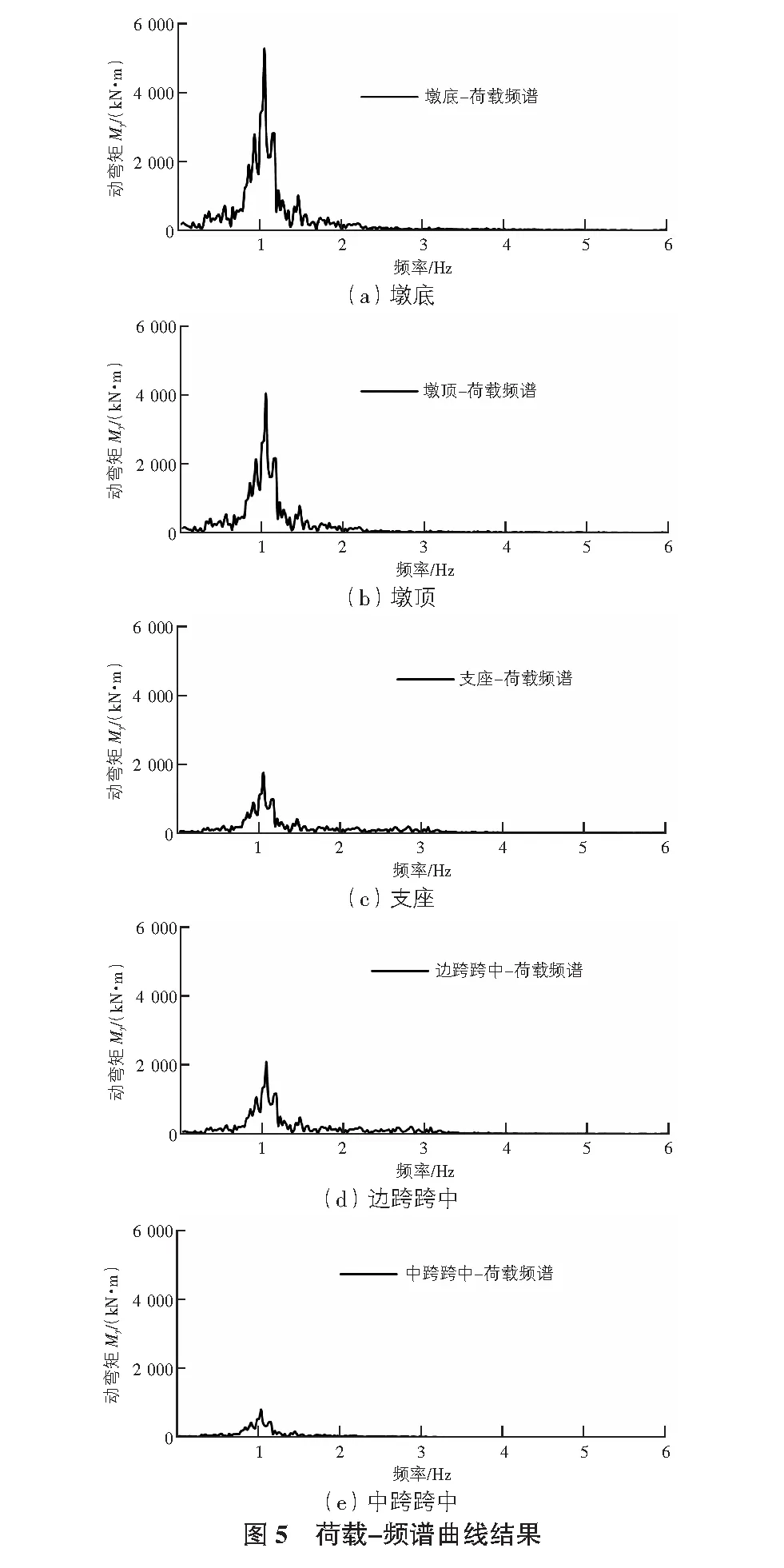
表3 最大彎矩與時間關系表

由圖5,表4可知,橋墩與主梁的最大彎矩均在頻率為1.05 Hz處,從橋墩墩底值墩頂的最大動彎矩值衰減較弱,由于橋墩本身剛度相對于橋墩較差,且橋墩為長條形立式結構,穩定性較差,動應力主要從橋墩墩底開始傳遞,導致最大動彎矩衰減不明顯;相比于橋墩的最大動彎矩,在主梁結構上的最大動彎矩明顯減小,其變化規律與荷載-時程曲線一致,可以看出,主梁中跨跨中的最大動彎矩減小最為明顯,從頻率角度上看,兩橋墩在同時受到EI-Centro地震波時,將同時通過墩底、墩頂、支座最后傳遞至中跨跨中,使得兩列波的頻率較為接近且相位差呈現相互抵消現象,由于在傳遞過程中地震波受到較大的干涉作用,沿中跨跨中區域逐漸減弱,針對此類現象,應特別注意邊跨的加固處理,減小地震波產生的影響。

3.3 鋼構橋整體震動響應

剛構橋整體震動響應的最大荷載分布曲線如圖6所示。

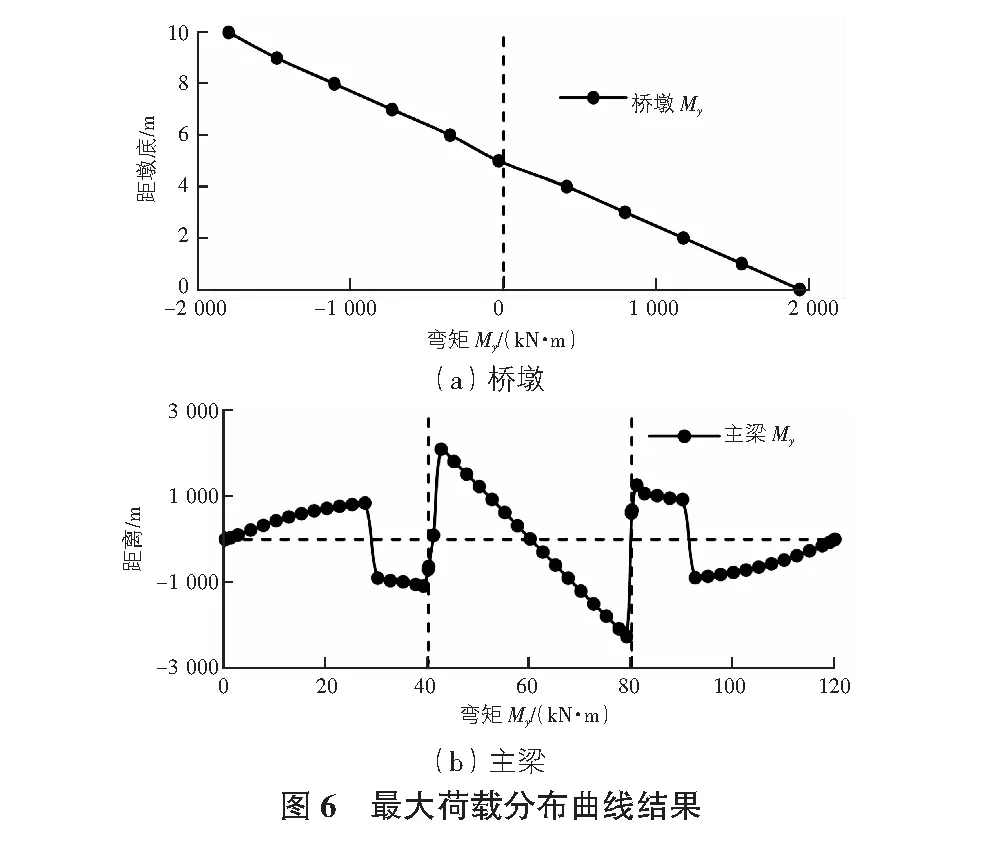
由圖6可知,橋墩墩底至橋墩墩頂的彎矩值傳遞具有從正彎矩至負彎矩方向呈現線性減小的趨勢,說明地震過程中,橋墩容易發生偏移,在抗震設計時,為強化橋墩的抗震能力,應加強基礎與橋臺的抗傾覆穩定性;從主梁的彎矩變化規律上看,支座處的彎矩在EI-Centro地震波作用下,邊跨與中跨容易出現突變現象,且左右兩支座正彎矩值與負彎矩相反,基本呈現為基于中跨跨中原點對稱的現象,表明支座處受剪嚴重,受震時容易產生剪切破壞,從邊跨上看,在離支座10 m～30 m范圍內,彎矩基本呈現線性減小的趨勢,從跨中上看,中跨邊緣受剪較大,最大值達到2 252.60 kN·m,在距支座12.5 m處減小至934.85 kN·m,因此,設計期間應根據抗震要求對主梁與橋墩剛性連接的兩邊合理區域內進行加固處理,防止支座開裂。

4 結論

本文通過基于EI-Centro地震波的加速度時程曲線,分析3主跨及兩橋墩的連續剛構橋荷載響應時程,獲得荷載-時程、荷載-頻譜曲線的變化規律,得到以下結論:1)根據荷載-時程曲線,墩底與墩頂值在同一時間內具有反方向運動的趨勢;邊跨跨中彎矩相比于支座處的彎矩稍微增大,中跨跨中彎矩相比于支座處的彎矩減小較為明顯。2)根據荷載-頻譜曲線,橋墩與主梁的最大彎矩均在頻率為1.05 Hz處,從橋墩墩底至墩頂的最大動彎矩值衰減較弱;隨著地震荷載從墩底、墩頂、支座、邊跨跨中、中跨跨中不斷向上傳遞,彎矩值逐漸衰減。3)根據最大荷載分布曲線,橋墩墩底至橋墩墩頂的彎矩值傳遞具有從正彎矩至負彎矩方向呈現線性減小的趨勢;支座處的彎矩在EI-Centro地震波作用下,邊跨與中跨容易出現突變現象,且左右兩支座正彎矩值與負彎矩相反,基本呈現為基于中跨跨中原點對稱的現象,設計期間應根據抗震要求對主梁與橋墩剛性連接的兩邊合理區域內進行加固處理,防止支座開裂。