例談新課程背景下RMI原則的教育價值

戴鍇寧 陳碧芬

【摘 要】 ??“關系映射反演原則”（簡稱RMI原則）是一種重要的數學思想方法，其實質是“矛盾轉移法”.在新課程背景下，對RMI原則進行教育價值的重新挖掘，發現在應用RMI原則的過程中可以培養學生聯系的眼光、辯證思維能力和創造性思維品質，潛移默化地落實數學學科核心素養的培養，并用例子解析如何實現這些教育價值.

【關鍵詞】 ?新課程；RMI原則；教育價值；數學學科核心素養

1 ??問題提出

新課程背景下，教育聚焦于人的核心素養的培養.教育要為學生的可持續發展和終身學習創造條件，使學生終身受益.數學教育的基本任務是促進學生思維的發展[1].數學方法論指導下的教學不僅關注具體數學知識的傳授，還關注滲透數學思想方法以幫助學生“用數學的思維思考世界”.而數學的思維方式承載了獨特的數學學科育人價值，是可教、可學的數學學科核心素養.因此，可立足“數學思維”教學培養學生數學學科核心素養.數學思維教學應當分兩個不同階段，即從“學會數學思維”走向“通過數學學會思維”，努力提升學生思維品質[2].第一步“學會數學思維”，在本文指RMI原則.第二步“通過數學學會思維”，即跳出了專業的范圍從更大的視角上看待數學教育的價值.那么，RMI原則的教育價值有哪些？如何實現這些價值呢？

2 ??RMI原則教育價值

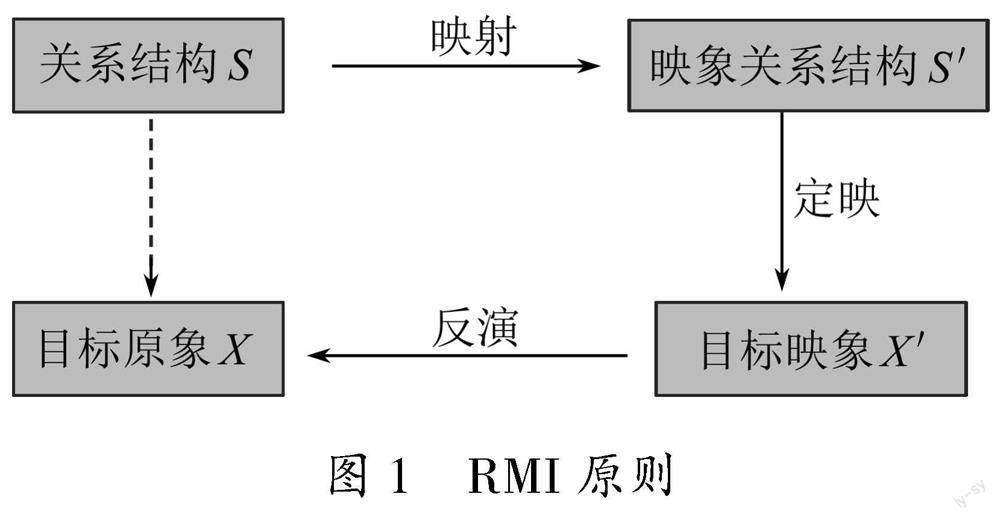
關系（Relationship）映射（Mapping）反演（Inversion）原則是由中國學者徐利治教授于1983年首先提出的.這一方法已被發現在數學中有著十分廣泛和重要的應用；如果從數學思想方法角度去進行分析，我們又可以提出更為一般的化歸原則.通常把彼此之間具有確定的數學關系的數學對象的集合稱為關系結構.明確的對應關系在數學中被稱為映射[3].映射是實現由未知到已知化歸的一個重要手段.由于在應用映射法解決問題過程中，有關的映射在相反的方向上又得到了應用，即首先用原來的問題去引出新的問題，后來又用相應的解答去引出所尋求的原來的解答.因此，有必要對相反方向上的映射重新區分為逆映射，即反演，同時求解新問題的解需要選擇合適的“數學手續”，這一過程稱為定映.最后有必要說明，在求解復雜問題時，可能需要多步的RMI程序.綜上所述，我們可以用框圖1的形式總結如下：

若跳出了數學專業領域看待RMI原則，其實質是“矛盾轉移法”，即培養了學生辯證思維品質和解決問題的能力.學生通過經驗的積累，使思維的變通性、靈活性得到提升，明白事物存在普遍聯系.RMI原則正是基于數學知識內部的聯系，用“聯系”的眼光構造合適的映射和定映方法，從而建立對應的橋梁.2.1 有助于形成聯系的觀點

“聯系”是數學學科知識結構化的主要特征.數學內部之間、數學與外部世界都存在普遍聯系.因此，教師在教學時要啟發學生用聯系的眼光思考，促進其在更加廣闊的思維空間中思考，通過類比、推廣、特殊化等方式解決問題.從RMI原則的應用過程看，有特殊與一般的聯系、靜與動的聯系、數與形的聯系等，是“聯系”實現了映射和反演.因為RMI原則中的“映射”是可逆映射，可定映映射.例如，解析方法可以用于處理平面幾何和立體幾何問題；通過對數映射，我們可把乘、除、開方等復雜的運算轉化為加、減、乘、除等簡單的運算；函數、方程、不等式可以相互轉化和化歸.這些基本思想方法都符合RMI原則.從這個意義上看待“RMI”的教育價值即實現了“用數學方式育人”，體悟到普適性的數學思想方法.

2.2 有助于提升學生辯證思維

辯證思維能力是科學思維能力的集中體現.學生辯證思維發展的不足，不僅影響看問題的全面性，而且也會影響人生觀和世界觀的形成.RMI原則的實質是“矛盾轉移法”，其應用范圍絕不限于數學領域.而矛盾的觀點是唯物辯證法的根本觀點，矛盾分析法是唯物辯證法的根本方法[4].RMI原則不僅可以用于得出肯定性解答，還可用以得出否定性解答，從矛盾中發現問題、尋找聯系，以新視角化解矛盾才能獲得內心平靜.例如，在轉化與化歸的過程中，懂得辯證分析，即將動點問題特殊化變為定點進行求解，或者尋找變化中不變的量.因此，RMI原則的教育價值對加強辯證思維能力，對學生形成科學的人生觀和價值觀具有重要意義.2.3 有助于提升學生創造性思維教育必須超越知識.知識當然重要，但是知識不是教育的全部內容[5].數學教育指向培養學生學會數學的思維.從RMI原則的應用過程看，創造性思維不僅體現在靈活地選擇“映射”工具上，也蘊含在定映過程的目標映象求解過程中.學生能靈活地選擇映射工具和數學手續，先漂亮地轉化問題，再更好地求解問題.例如：學生在解題時能準確地定位中學常見的函數法、向量法、參數法等來解決問題.另外，面對實際問題能用數學抽象通過構造函數模型，將實際問題轉化為函數問題，創造性地解決了現實的問題.同時，在定映過程中，能熟練地進行邏輯推理計算，展現清晰簡潔的思路.可以看出，學生尋求“映射橋梁”轉化問題、巧妙地求解問題的過程，體現了思維的靈活、變通特點，也是創造性思維的動力.因此，RMI原則指導下的教學可以提升學生創造性思維品質.2.4 有助于落實數學學科核心素養

落實數學學科核心素養是數學教學的導向標.核心素養之所以是“高級素養”，還有兩個原因，核心素養是跨學科的，高于學科知識; 核心素養是綜合性的，是對于知識、能力、態度的綜合與超越[6].RMI原則指導下的轉化和化歸過程中落實了“三會”，同時，在不同知識領域應用RMI原則，對于六大核心素養的側重也不同.

例如：在探究活動領域培養學生“數學建模”核心素養的過程中，首先，應用RMI原則對現實問題進行抽象轉化為數學問題，培養學生的“數學眼光”，完成映射；其次，通過數學手續分析求解數學問題的解，培養學生的“數學思維”，完成定映；最后，通過將求得的數學問題的解轉化為現實問題的解，培養學生的“數學語言”，完成反演. 在以上過程中，蘊含了數學育人的方式，發揮了數學的內在力量，“數學建模”的核心素養就潛移默化、潤物無聲地得到了落實.

3 ??案例解析

為了更好說明如何實現RMI原則的教育價值，本文將圍繞2018年浙江省高考數學第8題進行案例解析.

例題 ?已知四棱錐 S-ABCD 的底面是正方形， 側棱長均相等，E 是線段 AB 上的點（不含端點）， 設 SE 與 BC 所成的角為 θ1，SE 與平面 ABCD 所成 的角為 θ2，二面角 S-AB-C 的平面角為 θ3，則（ ?）.

A．θ1≤ θ2≤θ3 ??B．θ3≤ θ2≤θ1

C．θ1≤θ3≤θ2 ??D. θ2≤θ3≤θ1

3.1 理清目標原象，尋找映射實現聯系，完成轉化

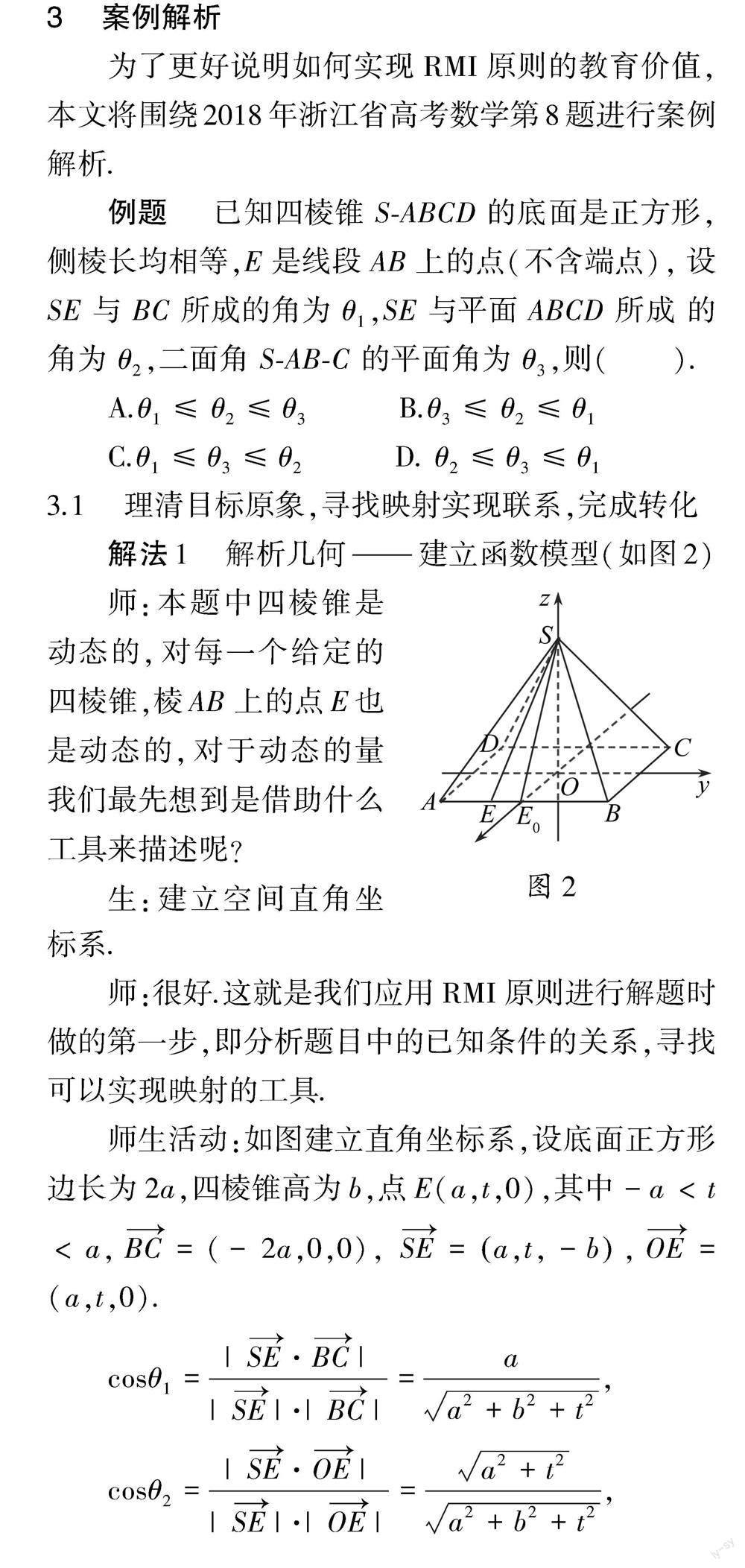
解法1 ?解析幾何——建立函數模型（如圖2）

師：本題中四棱錐是動態的，對每一個給定的四棱錐，棱AB 上的點E也是動態的，對于動態的量我們最先想到是借助什么工具來描述呢？生：建立空間直角坐標系.

師：很好.這就是我們應用RMI原則進行解題時做的第一步，即分析題目中的已知條件的關系，尋找可以實現映射的工具.

師生活動：如圖建立直角坐標系，設底面正方形邊長為2a，四棱錐高為b，點E（a，t，0），其中-a

cosθ1= |SE ·BC | |SE |·|BC | = a ???a2+b2+t2 ?，

cosθ2= |SE ·OE | |SE |·|OE | = ???a2+t2 ????a2+b2+t2 ?，

cosθ3= |SE ·OE0 | |SE |·|OE0 | = a ???a2+b2 ?.

解法2 ?極限思想——化動為靜（如圖3）

師：如果對于動態問題把握不好， 是否可以充分利用選擇題的特點，化動態為靜態呢？

生：可以嘗試特殊化點E的坐標，特殊化正四棱錐的大小.

師生活動：將正四棱錐特殊為所有棱長均相等的正四棱錐，將點 E 無限接近于端點 A.

解法3 ?化繁為簡——降維（如圖4）

師生活動：回憶空間角概念，所有空間角最后都降維成線線角，因此只要在正四棱錐內作出 θ1，θ2，θ3即可.記E0為棱 AB 的中點，頂點S在底面的射影為 O（易知O為底面正方形的中心） ，過點O作OO1∥AB，過點 E 作 EO1∥E0O，則 易證EO1⊥SO1． 聯結 SE，SE0可得∠SEO1=θ1，∠SEO=θ2， ∠SE0O=θ3 分析 ?理清題目中目標原象的特點是利用RMI原則進行解題的首要步驟.教師需要幫助學生梳理已知條件和回憶相關的知識，尋找構建映射的方法，并介紹常用的“映射工具”，如參數法、數形結合法、構造法等等.解法1、解法2和解法3選擇不同的映射方法，建立了知識的聯系.與此同時，不同映射工具的選取和定映求解的實現，體現了學生思維的靈活和變通特點.教師引導學生從不同角度思考，激活創造性思維，培養學生“求異”的眼光.其中解法2的極限思想對于學生思維訓練價值更大，突出靈活和變通特點.同時，本題也有利于學生直觀想象和數學建模素養的培養.

3.2 分析映象結構，尋找演算工具，靈活推理，完成定映師：將原來的問題進行轉化后，就需要對目標映象進行求解，那用什么方法比較好呢？生：解法1直接進行代數化簡即可；解法2假設當點E無限接近端點A時求解；解法3可以利用正切值來比較空間角的大小即可.師生活動： 解法1 ?化簡比較結果

易得cosθ1≤cosθ3，又cos2θ2=1- a2 a2+b2+t2 ，cos2θ3=1- b2 a2+b2 ，所以cosθ3≤cosθ2，故cosθ1≤cosθ3≤cosθ2.

解法2 ?點E無限接近于端點A，cosθ1→ 1 2 ，cosθ2→ ???2 ?2 ，cosθ3= ???3 ?3 .

解法3 ?tanθ1= SO1 EO1 = SO1 E0O ≥ SO E0O =tanθ3，又tanθ3= SO E0O ≥ SO EO =tanθ2.

分析 ??實現關系結構轉化之后，接下來需要求解映象結構中的解.求解過程即為定映過程.實現定映需要學生掌握一系列的“數學手續”.凡是由數值計算、代數計算、解析計算、邏輯演算以及數學論證等步驟構成的形式過程都稱之為“數學手續”[3]. 教師對于學生基本知識和基本技能的考查和訓練是有必要的.解法2采用了化動態為靜態，體現了辯證思維特點和矛盾轉移的方法.解法1，2，3都通過不同的 “數學手續”恰當地表示出了函數值的大小，其過程突出了邏輯推理和數學運算的學科核心素養的培養.3.3 反演回歸目標原象檢驗結果，注意思維嚴密性師：得出函數值后，需要做什么？

生：再次檢查題目中要求的量與當前求得的解是否一致.師生活動：

解法1：由cosθ1≤cosθ3≤cosθ2，即θ2≤θ3≤θ1.

解法2：由cosθ1= 1 2 ，cosθ2= ???2 ?2 ，cosθ3= ???3 ?3 ，即θ2≤θ3≤θ1

解法3：由tanθ1≥tanθ3≥tanθ2，即θ2≤θ3≤θ1.

師：很好.這也就是要反演回原來的題目，檢查目標原象的解的正確性.最后，我們嘗試運用RMI原則來表示三種解法的程序框架圖： ???解法1 ?如圖5所示：

解法2 ?如圖6所示：

解法3 ?如圖7所示：

分析 ?思維的邏輯性與嚴密性是理性思維的兩個基本特征.因此，教師應該注重學生良好的習慣，在求出目標映象的解之后，我們不能忘記要反演回歸原問題的解，并檢驗結果的合理性.尤其在數學模型解決現實模型時，應該允許一定的誤差.學生思維培養不是“無源之水，無本之木”，它是“接地氣”的.回顧整個理解RMI原則解決問題過程，它要求學生有良好的學習基礎，并通過具體教與學過程來支撐.解法1，2，3都需要學生有聯系的眼光和辯證轉化 的思維.解法2的極限思想相對較難，但對學生思維的訓練和創造性品質的培養有相對的價值.

總之，新課程背景下的數學教學要克服重教書輕育人的傾向，強調關注數學學科思想、數學思維方式的教學.RMI原則立足數學本身的學科特點，蘊藏了普遍的教育價值和廣闊的發展空間.本文只體現了其在數學應用中的“冰山一角”.就教學工作而言，只有注意數學思想方法的分析，才能將數學知識“講活”“講懂”“講深”.數學方法論、數學教育學都不是封閉的體系，都會隨著時代發展而發展.站在新時代，作為教育工作者應面向未來，加強自我革新，努力積極實踐，那么RMI原則下的教學必將結出更多的碩果.

參考文獻

［1］ ?鄭毓信.從“教學教育的基本目標”談起——中學視角下的“數學教學的關鍵”（2）［J］.中國數學教育，2021（21）：3-5.

［2］ ?鄭毓信.數學思維教學的“兩階段理論”［J］.數學教育學報，2022，31（01）：1-6.

［3］ ??鄭毓信.數學方法論［M］.南寧：廣西教育出版社，1991：87.

［4］ ?彭壽清.習近平新時代中國特色社會主義教育思想的哲學基礎［J］.西南大學學報（社會科學版），2018，44（01）：12-21.

［5］ ?錢穎一.批判性思維與創造性思維教育：理念與實踐［J］.清華大學教育研究，2018，39（04）：1-16.

［6］ ?褚宏啟.核心素養的概念與本質［J］.華東師范大學學報（教育科學版），2016，34（01）：1-3.

作者簡介 ?戴鍇寧（1997—），女，浙江金華人，碩士研究生；主要研究學科教學（數學）.

陳碧芬（1979—），女，浙江奉化人，副教授，碩士生導師；主要研究數學課程與教學論.