基于連接元法的多尺度裂縫性油藏數值模擬1)

湛文濤 趙 輝 饒 翔 劉 偉 徐云峰

(長江大學石油工程學院,武漢 430100)

1 引言

隨著人工壓裂技術相關材料、方法和工藝取得新的進展,水平井壓裂技術成為超低滲油藏、致密油藏等非常規油氣資源商業化開發中的主要技術手段[1].在壓裂過程中,地層中會形成許多導流裂縫,相比于天然裂縫,導流縫通常尺度較大,滲透率很高,但對于油藏區域而言,裂縫的尺度相對小,水力壓裂縫網儲層具有多尺度的特征.裂縫幾何(形狀,長度以及方向)對流體流動具有顯著的影響[2-3],分析這些影響因素,裂縫油藏數值模擬模型是必要的.

目前裂縫性油藏數值模擬方法主要分為兩類,連續介質模型和離散介質模型[4],其中,連續介質模型主要包括等效連續介質模型[5]和雙重介質模型[6-7].在連續介質中,裂縫和基質被處理成等維度的離散單元.在離散介質模型中,n維油藏系統中的裂縫被作為n-1 維處理,即在二維的油藏系統中,裂縫被認為是一維的線段,而三維問題中裂縫則是二維的平面.這是這兩種方法在處理裂縫形態上本質的區別.在連續介質模型和離散介質模型下,一些學者采用有限差分[8-11]、有限元[12-14]和有限體積[15-17]等數值模擬方法進行流動模擬計算,這些數值模擬計算方法都是基于網格剖分離散表征計算域.在連續介質模型中,裂縫和復雜邊界幾何的精細描述需要更小的網格,這會造成數百萬計甚至數億計的模型自由度,極大增加計算耗時.在離散介質模型中,雖然將裂縫降維處理,能夠降低裂縫表征的難度,但高質量的匹配性網格難以生成.嵌入式離散裂縫模型基于正交網格的基質離散方案無法適用于實際油藏復雜邊界,針對該問題程林松等[18]提出基于兩套節點的格林元法耦合嵌入式裂縫模型能適用于任意形態的基質網格,可實現復雜油藏邊界問題的求解,但該計算過程相對復雜.

近年來,無網格法在計算力學以及流體動力學領域得到了廣泛應用[19-22],常用的無網格法有加權最小二乘[23]、廣義有限差分[24]、無單元Galerkin 法[25]以及光滑粒子流體運動學法[26].無網格法通過點云的方式離散計算域,能夠更加靈活地刻畫裂縫和復雜邊界,對于油藏復雜幾何的描述相比于網格類方法更加簡單.一些學者將無網格運用于裂縫性油藏,比如將無網格法應用到裂縫擴展建模中,結合應力分析裂縫幾何形狀演變過程[27].基于無網格廣義有限差分法和嵌入式離散裂縫模型,建立一種裂縫性油藏數值模擬無網格方法[28],驗證其方法對于復雜幾何形態刻畫的優勢性,但該方法還存在著計算效率問題和不能直觀反映井節點間的連通關系.基于井間連通性思想[29-33],趙輝等[34]引入廣義有限差分理論,建立非歐物理連通網絡等效模型,推導滿足物質守恒且具有物理意義的滲流特征參數,提出一種新的油藏數值模擬計算方法—無網格連接元法(connection element method,CEM),為油藏數值模擬提供了新思路.基于連接元核心思想,定義無網格節點控制體積,Rao 等[35]發展了擴展有限體積法,本質上它是連接元法的全隱式格式.

目前對于復雜裂縫網絡的刻畫,傳統方法存在著匹配性網格自適應生成困難和結構化網格難以適用于裂縫網絡和油藏邊界的復雜幾何等問題.在應用于實際油藏時,數值模型的網格數將十分巨大,導致計算效率低、歷史擬合難,同時難以獲取注采井間的動態連通性以及流線追蹤.本文將連接元法應用于裂縫性油藏的開發動態模擬,不同于網格體系(匹配網格或者結構化網格),針對多尺度裂縫儲層的表征,連接元法沿著裂縫的走勢配置相應的不同尺度的連接單元,精細刻畫裂縫.該方法具有無網格特征,離散表征更加自由和靈活,能夠更加容易刻畫裂縫和復雜油藏邊界.此外,物理連通網絡的連接關系相比于網格體系和無網格點云能夠更加直觀揭示井間的連通關系.

2 裂縫油藏連接元法基本原理

區別于網格體系,該方法離散油藏計算域時不需要網格剖分,能夠避免網格體系表征油藏復雜幾何(裂縫、斷層以及不規則邊界)的困難.從流動的角度,將油藏計算域離散成為一系列連接單元構成的連接網狀拓撲結構,采用全隱式的離散方案基于牛頓迭代法可實現滲流控制方程的高效求解.以油水兩相流為例,介紹裂縫性油藏連接元方法的基本原理.

2.1 裂縫油藏連接元單元體系構建

在油藏數值模擬方法中,基于網格體系的離散方式,其主要目的是獲取離散后的網格單元體間的連接拓撲結構,按照其拓撲連接關系分析勢場和流場的相互作用關系.換而言之,網格剖分的本質是建立離散單元體之間的連接關系,但基于網格體系的離散會限制其連接關系,它們只能建立相鄰網格間的連接關系,比如正交網格、三角剖分網格、PEBI網格離散.連接單元體系是一種物理網絡結構,它是由節點間的連接單元所構成.如圖1,利用連接單元將某個油藏離散為連接單元體系.顯然,基于連接單元體系離散避免了網格剖分對于不規則油藏邊界和裂縫的匹配性網格離散的困難,尤其對于尺度差異大的裂縫表征.這種方案幾何離散更加簡單,不再受限于網格相鄰關系,而是更加靈活直觀地表征節點間的相互關系.

圖1 油藏的連接單元離散Fig.1 Reservoir discretization based on connection element

在實際油藏開發過程中,往往需要在地層中布置合理的生產井和注入井.在油藏數值模擬中,部署的井往往是作為源匯項處理.基于網格體系的傳統數值模擬對于源匯項問題,往往是在背景網格的控制域上采用積分的方式處理.基于連接單元體系的節點沒有實質控制域,為方便處理帶有源匯項的物理問題,在節點處需要給出一個控制體積域的概念.下面基于物質守恒原理給出節點控制域的定義,所有節點間的控制域不相交,且所有控制域之和為整個油藏區域

其中,Ω 是整個油藏控制域;Ωi是節點i的控制域;VΩ是油藏總體積;Vi是節點控制體積.

2.2 滲流特征參數計算

連接單元體系的本質將實際三維流場轉換為由一維連接單元構成的物理連通網絡,為在連接單元體系上對滲流方程進行計算,需要建立表征連接單元的滲流特征參數.定義節點間連接傳導率來表征連接單元的流體滲流能力,連接傳導率與勢場(如滲流問題的壓力場)中對勢的計算(壓力)相關.下面以兩相流控制方程為例,推導裂縫性油藏連接單元滲流特征參數的計算方法.

2.2.1 基質間滲流參數表征

首先給出雙重介質基質系統兩相流滲流控制方程

式中,km和krσ分別是基質系統絕對滲透率和相對滲透率,mD;μo和 μw是油和水黏度,mPa·s;? 是哈密爾頓梯度算子;pσ,m是基質層壓力,MPa;sσ,m是基質層飽和度,1;t是時間,d;qosi是地面標況下的體積流量(源匯項),d-1;δ是狄拉克函數,1;τmf是基質與裂縫之間物質交換的量.

對于式(2),壓力擴散項在節點控制域 Ωi內積分,得到

式中,i為影響域中心節點,該影響域包含著其他ni個節點,代表以i節點為中心節點計算的連接單元(i,η) 的傳導率.考慮以節點j為中心的影響域(包含節點i),該影響域包含著其他nj個節點,可以得到

根據連接單元物質平衡原理及所有節點的控制體積之和等于油藏體積的原則,可以求得每個節點的控制體積[28,34-35],進而可以定義基質節點間的連接單元 (i,j)的傳導率為

2.2.2 顯式裂縫間滲流參數表征

首先給出雙重介質裂縫系統兩相流滲流控制方程

式中,kf和krσ分別是裂縫絕對滲透率和相對滲透率,mD;μo和 μw是油和水黏度,mPa·s;? 是哈密爾頓梯度算子;pf,σ是基質層壓力,MPa;sf,σ是基質層飽和度,1;t是時間,d;qσ,well是地面標況下的體積流量(源匯項),d-1;δ是狄拉克函數,1;τmf是基質與裂縫之間物質交換的量.

對于裂縫系統而言,類似于網格體系的傳導系數定義裂縫層兩裂縫節點間的傳導率為

2.2.3 兩相流基質與顯式裂縫間滲流參數表征

對于基質與裂縫間物質交換的刻畫,Moinfar等[36]將嵌入式離散裂縫模型(EDFM)運用到三維問題,定義基質網格向裂縫網格的傳導系數為

式中,A是裂縫與基質的界面面積,m2;k是滲透率張量,n為 法向向量,〈d〉為f與m之間的平均法向距離,m.

然而本文方法對于節點控制體積沒有一個具體的形狀描述,針對裂縫與基質的界面面積A的刻畫,采取節點控制域內裂縫總長度Lf,i與裂縫高度hf,i的乘積.對于某中心節點i,Lf,i被取作所有以節點i為端點的裂縫連接單元的一半的總和

式中,Λ表示以節點i為端點的裂縫連接單元的其他端節點構成的集合;Lf,iζ是以節點i和節點 ζ為端點的裂縫連接單元 (i,ζ)的長度,m.

在處理基質節點與裂縫節點間的物質交換量的表達式為

本文考慮裂縫貫穿整個油藏儲層厚度,即裂縫高度與油藏儲層厚度h相同.是節點i的控制域內基質與裂縫竄流的調和平均滲透率,mD.d是裂縫與基質竄流的等效法向距離,m

因此定義基質層與裂縫層竄流的傳導率為

2.3 滲流控制方程離散求解

基于局部雙重介質的裂縫油藏兩相流滲流控制方程如下.

基質系統

裂縫系統

結合離散節點控制域 Ωi可將方程離散,其滲流控制方程的離散形式如下

對于油相和水相的相對滲透率,采用油藏數值模擬中常用的迎風格式,即

邊界條件主要是第一類邊界條件(Dirichlet 邊界)和第二類邊界條件(Neumann 邊界).處理第二類邊界條件時,需要在邊界處加入虛擬點,輔助計算邊界處的導數[35].虛擬點的加入方式在參考文獻里有詳細介紹,這里不再贅述.

2.4 連接單元體系路徑追蹤

基于網格體系的方法難以直觀獲取各井之間的相互作用關系.目前,針對裂縫油藏尚未形成簡單實用的連通性定量表征方法,而基于連接體系的連接元法可通過INSIM-FPT[31]中的路徑搜索算法獲取各節點之間的所有流動路徑及各流動路徑的劈分系數.劈分系數的數學描述如下,假設在第n個時間步,上游節點i與下游節點j之間直接相連(即存在連接單元),則節點i到節點j的劈分系數為[31]

式中,是與節點i相連的下游節點數.

劈分系數反映了上游節點處的流體流到下游節點的比例,體現了節點之間的流動相互作用,從而可以直觀揭示注水受效、水竄識別等礦場實際問題.此外,在某一時間步計算得到各節點控制體積的平均壓力后,在無網格連接體系的基礎上會形成壓力高低判別的有向圖,即對于某連接單元i-j,如果在第n時間步,節點i的壓力高于節點j,則連接單元i-j的方向定義為由i指向j.在這樣一個有向圖的基礎上,可以采用圖論中的路徑搜索算法獲取各節點之間的所有路徑.

3 應用

本節主要的目的是探索裂縫性油藏連接元的計算性能.下面給出幾個數值算例來驗證本文方法的有效性和優越性,包括平行多縫單相流,復雜邊界平行多縫兩相流.引入L2范數誤差函數,以精細網格剖分的EDFM 作為參考解,對比壓力、含水飽和度場圖以及含水率曲線.此外引入路徑追蹤方法,可以在連接單元體系下獲取流動路徑和分析井節點間的連通性,以此體現本文方法獨特的優越性.下面給出兩個算例相同的物性參數見表1

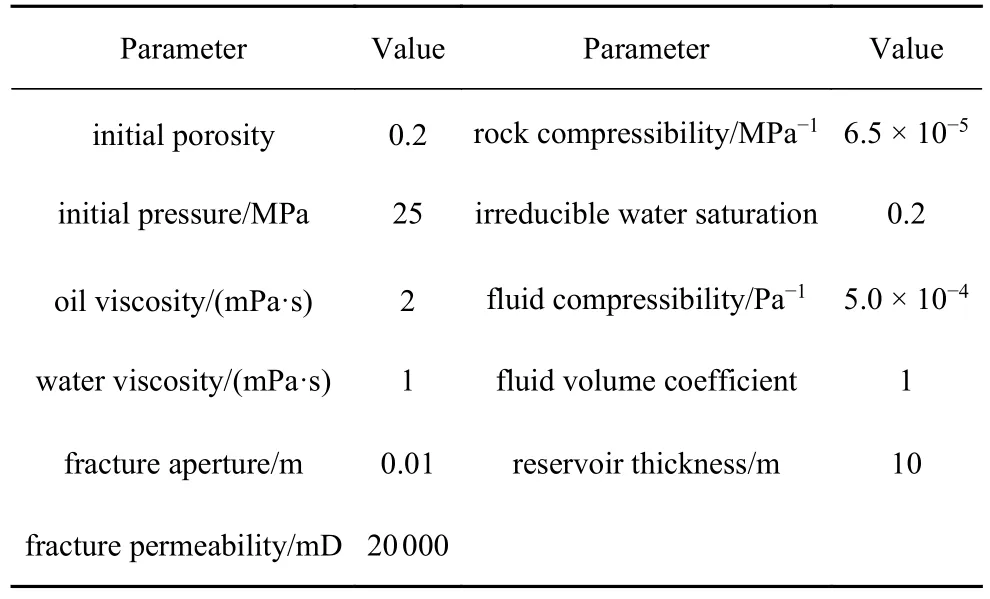
表1 油藏物性參數Table 1 Physical parameters of reservior

其中,u(i) 是計算值,uref(i)是參考值,T是節點(網格)總數.

3.1 傾斜平行縫網單相流

油藏尺寸為960 m×520 m×10 m,油藏中心一口水平井P1,在地層中射開6 條平行傾斜裂縫,裂縫縱向上貫穿油藏,裂縫厚度與油藏厚度相同.基質滲透率0.1 mD,以每天10 方的產量進行衰竭開發,模擬計算生產500 天.油藏網格剖分為120×65×1,網格大小Dx=Dy=8 m,Dz=10 m,網格總數7800,采用嵌入式離散裂縫模型精細解作為參考解.如圖2 (a)所示,給出了24×13 粗化網格的嵌入式離散裂縫油藏模型,網格大小Dx=Dy=40 m,Dz=10 m,網格總數312.如圖2 (b)所示,以等間距Dx=Dy=40 m,Dz=10 m 的24×13×1 的構建連接元模型,影響域半徑為,總節點數312,連接單元總數2173.

圖2 裂縫性油藏模型離散Fig.2 The discretization of fractured reservoir model

根據滲流控制方程(19),對于單相流問題,通過EDFM 方法和CEM 方法求解壓力,計算整個油藏的壓力場分布.圖3～圖5 分別是EDFM 精細網格剖分、EDFM 粗化網格剖分和CEM 法在第100 天和第500 天的壓力場圖.結果表明,本文方法與參考解是一致的,說明了該方法的有效性和正確性.在24 ×13 配點模型下,統計計算機CPU 耗時(計算機型號:12 th Gen Intel(R) Core(TM) i5-12400 F),基于精細網格的EDFM 計算耗時138.14 s,粗化網格的嵌入式離散裂縫模型計算耗時29.76 s,壓力場圖的計算精度96.2%,而連接單元法的計算耗時31.24 s,壓力場圖計算精度99.1%.在計算耗時相當的情況下,計算精度提高了2.9%.

圖3 EDFM 計算壓力,8 mFig.3 The pressure calculation of EDFM,8 m

圖4 EDFM 計算壓力,40 mFig.4 The pressure calculation of EDFM,40 m

圖5 CEM 計算壓力,40 mFig.5 The pressure calculation of CEM,40 m

下面從影響域半徑和配點間距兩個方面分析本文方法的穩定性.首先采用均勻離散配點的方式離散油藏計算域,分別取如圖6 所示的3 種不同節點影響半徑構建連接單元體系,需要說明是,從物質流動的角度出發,共線的3 個點,只取相鄰兩點構建連接單元,計算不同模型的誤差如圖7 所示,結果表明,過小或者過大的影響域半徑會降低計算精度,這個結果也與無網格法的影響域半徑對計算精度的敏感性一致.因此,為獲取相對高的計算精度,本文在算例驗證中影響域半徑取.

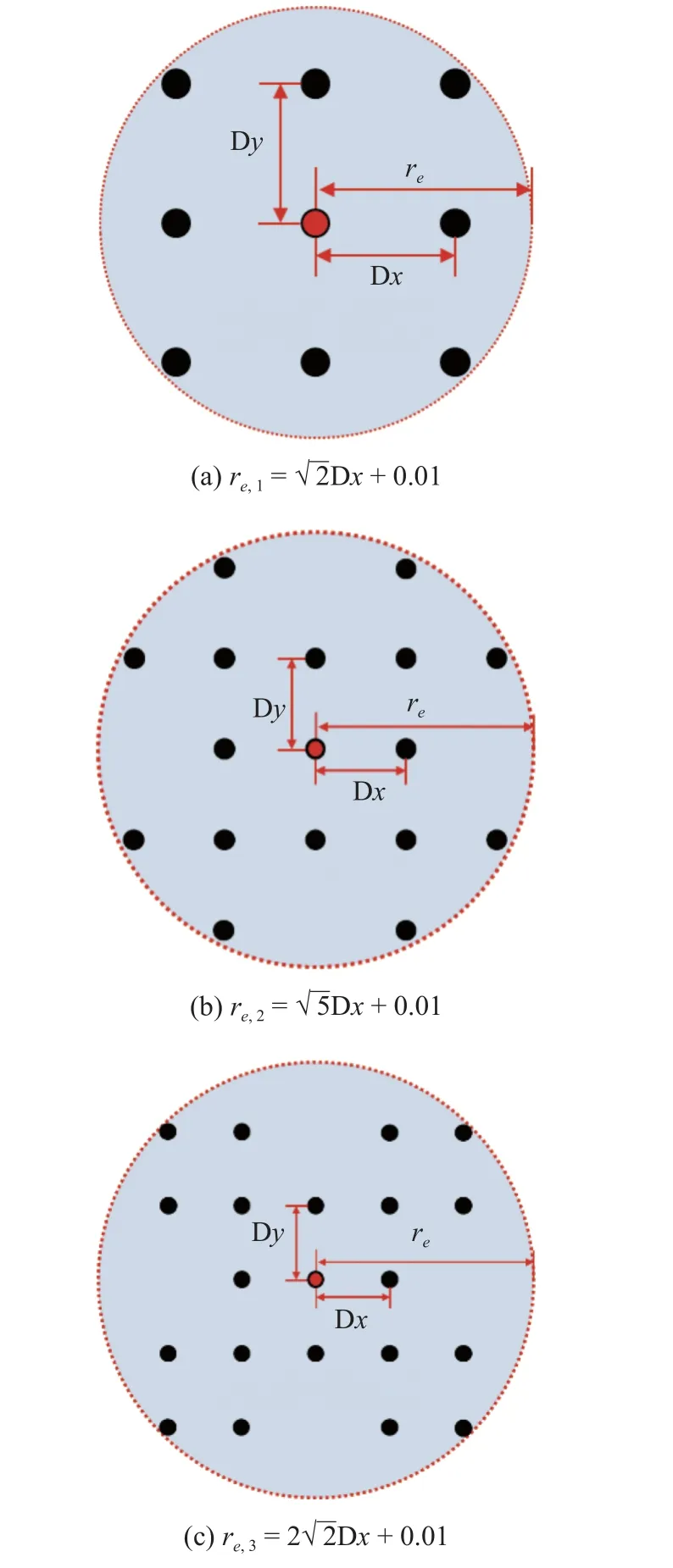
圖6 不同影響域半徑示意圖Fig.6 Diagram of different influence radius

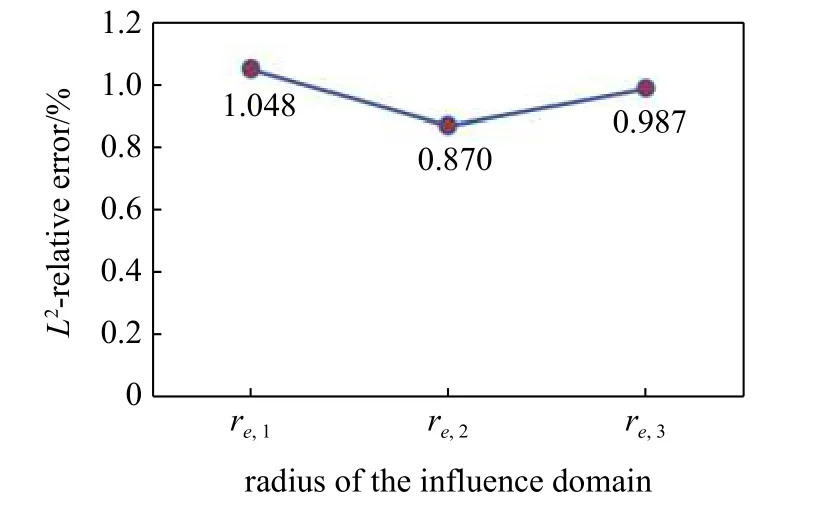
圖7 不同影響域半徑壓力計算誤差Fig.7 Calculation error of pressure with different radius of influence

圖2 中已經以等間距Dx=Dy=40 m,影響域半徑re=構建連接元模型,下面分別給出以等間距Dx=Dy=20,10 m,兩種布點方案,影響域半徑+0.01構建連接元模型,計算100 d 和500 d 的壓力分布如圖8 所示.圖9 是3 種不同配點間距連接元模型的壓力計算誤差,結果表明,隨著配點間距越小,計算精度越高,說明本文方法具有良好的收斂性.

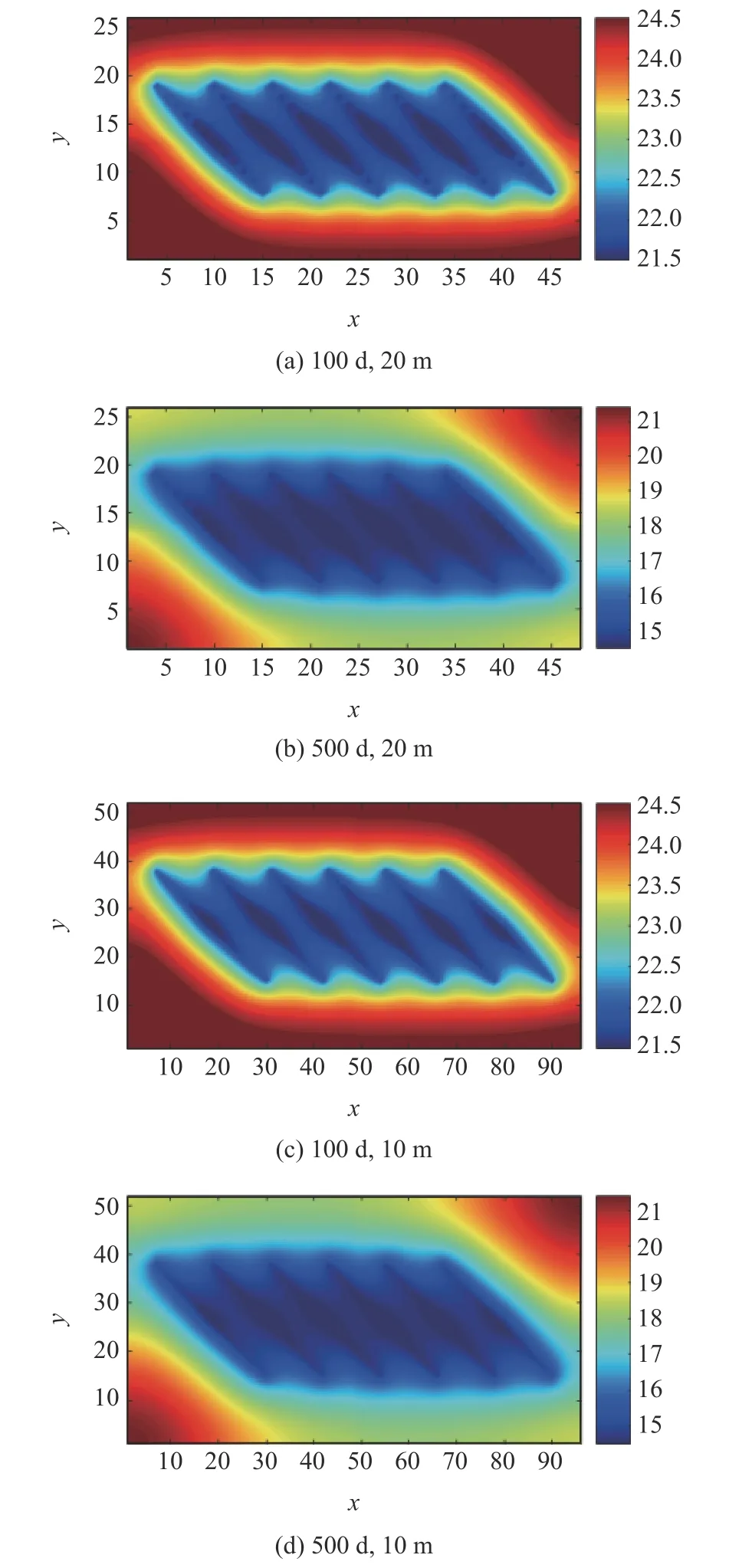
圖8 不同間距布點CEM 計算壓力Fig.8 The pressure is calculated by CEM at different collocation intervals

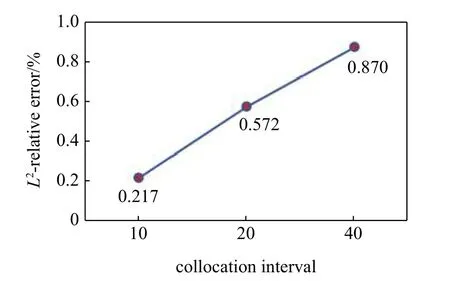
圖9 不同間距布點CEM 壓力計算誤差Fig.9 Calculation error of CEM pressure at different collocation intervals

3.2 不規則邊界平行縫網油水兩相流

設計一個不規則邊界油藏的概念算例,在油藏中布置有3 口水平生產井以及7 口注水井,裂縫縱向上貫穿油藏,裂縫厚度與油藏厚度相同,油藏區域如圖10 (a)所示.油藏總體積為4.212 ×105m3,基質滲透率10 mD.3 口水平井均以350 m3/d 產液量,7 口注水井以150 m3/d 注入量的生產制度進行開發.如圖10 (b),以網格大小為Dx=Dy=4 m,Dz=10 m 離散油藏計算域,網格總數33325,以此精細網格剖分的EDFM 數值模型作為參考解.圖10(c)是連接元油藏離散模型,節點總數1053,連接單元總數7868.連接單元法沿著油藏邊界配置相應的節點,相比于網格離散,能更靈活地匹配實際油藏邊界.為了對比邊界處的滲流場的計算精度,在油藏左下邊界上取一個觀測點A(如圖10 (b)),對比注采過程中壓力和含水飽和度的計算結果.

圖10 不規則油藏模型Fig.10 Irregular reservoir model

以精細網格剖分EDFM 計算壓力、含水飽和度、含水率以及產油速度等參數作為參考解.結合兩相流的控制方程離散格式,采用連接單元法計算油藏的壓力和飽和度分布,求解井點的含水率以及產油速度等參數.如圖11,分別給出了第500 d EDFM 與CEM 計算的壓力結果.圖12 是第100 d和500 d EDFM 與CEM 計算的飽和度,本文方法計算的結果與參考解一致.圖13 是兩種方法計算觀察點處的壓力和含水飽和度動態曲線.結果表明,本文方法在邊界處具有較高的計算精度.通過壓力和飽和度的計算,說明了裂縫性油藏連接元法具有較高的計算精度.此外,對比了3 口水平生產井的含水率和產油速度等動態參數,如圖14 所示,連接元的井點參數計算結果與參考解結果一致.基于精細網格的嵌入式離散裂縫模型計算耗時621.41 s,連接單元法的計算耗時126.53 s,3 口生產井P1,P2 和P3 的含水率的計算精度分別為90.41%,88.26% 和91.89%.連接單元法在較少的節點體系下取得了較高的計算精度,相比于精細的嵌入式離散裂縫模型而言,計算速度提高了近5 倍.因此,本文方法能夠取得計算精度和計算效率的更優平衡.此外,引入路徑追蹤方法,計算7 口注水井的劈分系數,如圖15 所示.

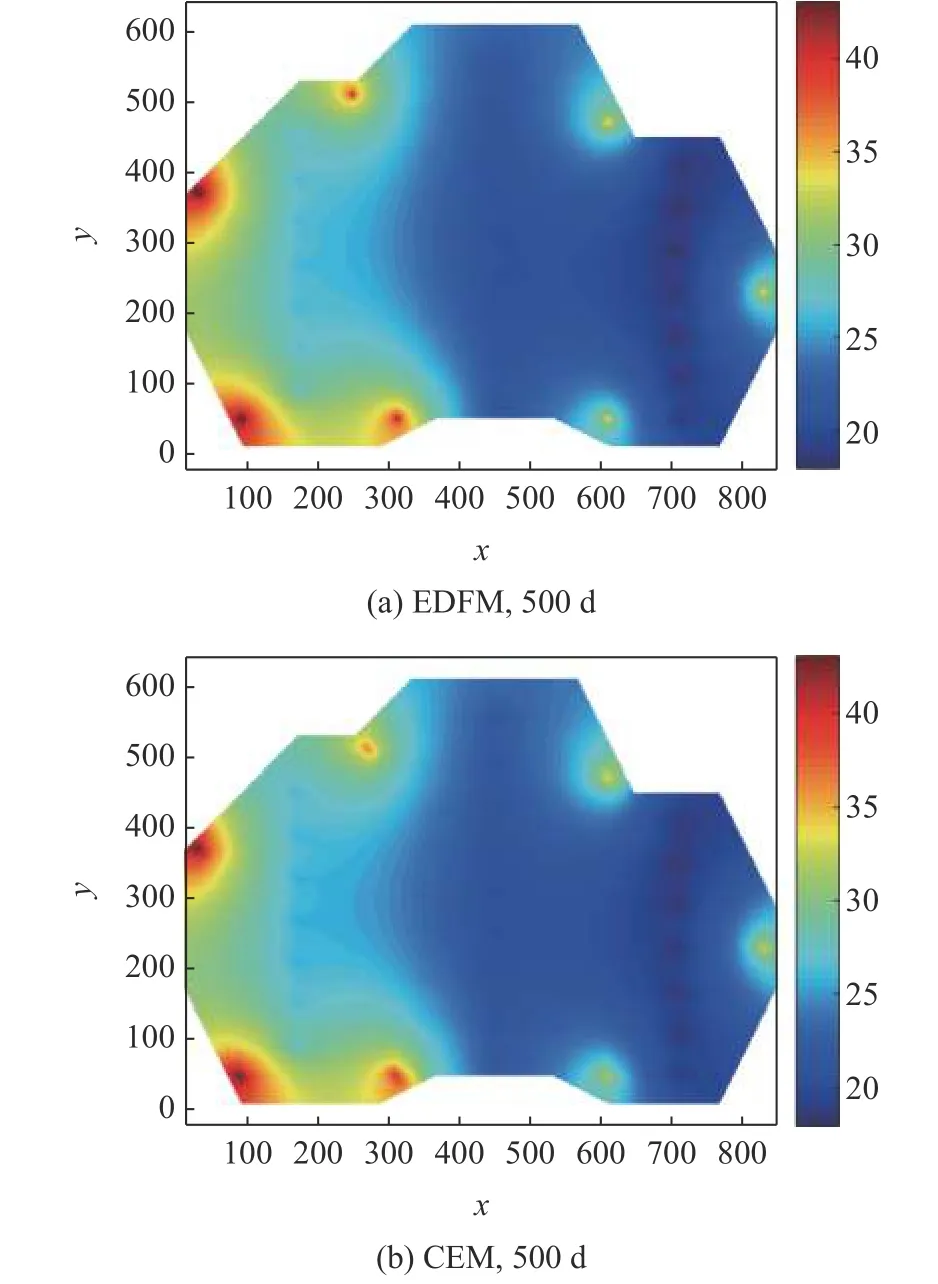
圖11 壓力場圖Fig.11 Pressure profile

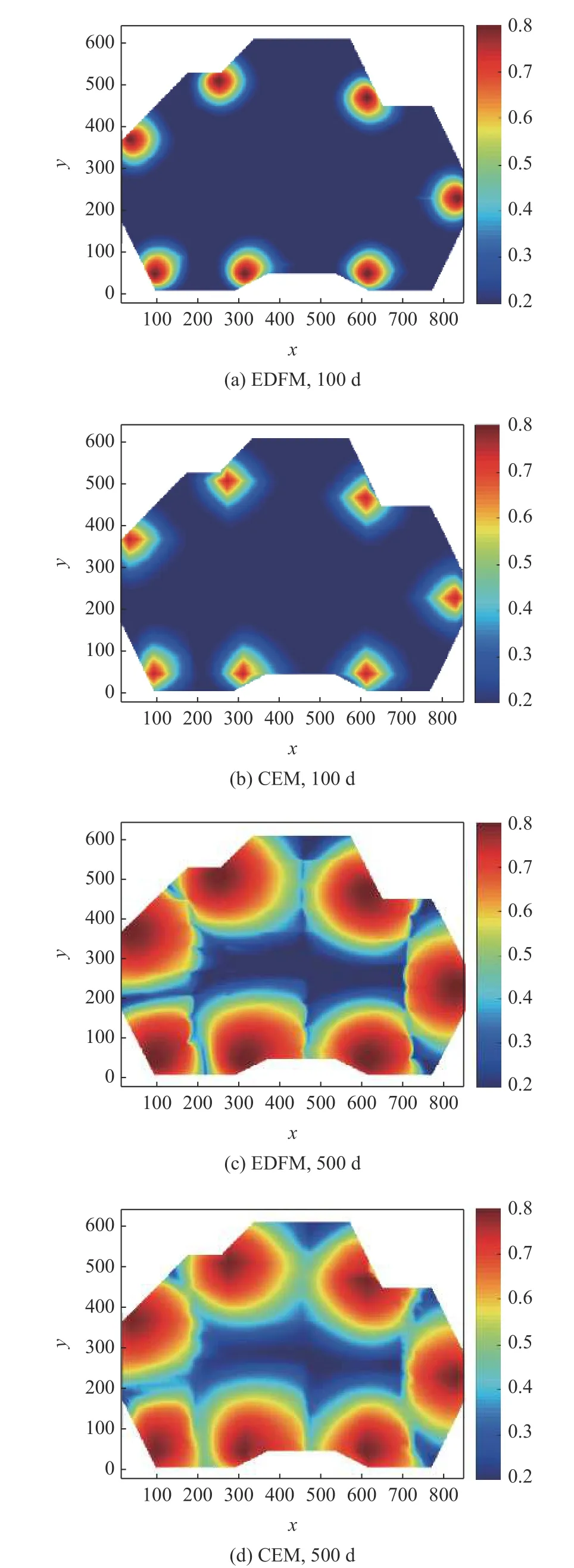
圖12 含水飽和度場圖Fig.12 Water saturation profile

圖13 邊界觀測點結果對比Fig.13 Comparison of boundary observation points

圖14 含水率與產油速度曲線Fig.14 Water cut and oil rate curves

圖15 注采連通示意圖Fig.15 Injection-production connectivity profile

4 結論

(1)本文構建一種基于無網格連接單元體系的裂縫性油藏數值模擬方法,該方法具有無網格特征,相比于網格離散,對于裂縫幾何形態、分布以及不規則油藏邊界的精細刻畫非常自由靈活,能夠更加適用于裂縫性油藏復雜幾何特征的刻畫.

(2)相較于傳統方法,本文方法在離散滲流控制方程時,構造了未知函數導數的多點差分近似格式,具有更高的估計精度,即使在相對粗化的模型下,也能具有更加豐富的節點(網格)間連接拓撲結構.因此,該方法能夠通過粗化模型,降低油藏數值模型計算自由度,提高計算效率的同時,保證了較高的計算精度,能夠取得計算精度和計算效率的更優平衡.

(3)相較于傳統方法,本文方法能夠在粗化模型下,利用路徑追蹤算法高效直觀地獲取節點間的相互作用,計算無網格連接體系下各流動路徑的注水劈分系數,實現裂縫性油藏井間連通關系的定量識別.