運動副分布順序對并聯機構運動學與動力學性能的影響

沈惠平 仲 銳 李 菊 李 濤

(常州大學現代機構學研究中心, 常州 213016)

0 引言

三自由度純平移和純轉動并聯機構在抓取及調姿等方面已有較多的研究與應用[1],但具有轉動和移動特性混合的并聯機構研究和應用相對較少。

HUNT[2]于1983年設計了一種含寄生運動的3-DOF空間機構,ZHANG等[3]對2T1R的平面并聯機構類型進行了綜合并實現了模塊化設計,但缺少對機構的運動學分析;劉艷敏等[4]研究了2T1R機構的綜合方法,并優選了部分新機型;余順年等[5]提出了一種以兩平移一轉動并聯機構為主體的新型中醫推拿機器人機型,并求出其運動學正反解的解析解;WANG等[6]提出了一種Cylindrical型兩平移一轉動并聯機構;楊寧等[7]根據基于螺旋理論對兩平移一轉動型并聯機構的結構綜合進行研究;REFAAT等[8]根據位移李群理論對三自由度運動并聯機構進行型綜合研究;張彥斌等[9]根據線性變換理論,對無奇異完全各向同性2T1R型空間并聯機構進行型綜合;楊廷力等[10-11]基于單開鏈單元對2T1R型并聯機構進行了型綜合,得到多種含有平面閉回路結構的新型機構;SHEN等[12]設計并分析了一類具有解耦運動和符號式位置正解的2T1R并聯機構,并研究了優化支鏈布置對運動學、動力學和剛度的影響;TETIK等[13]利用回路方程的雅可比矩陣確定了3-RRS并聯機構的奇異性;SUN等[14]使用邊界搜索方法求解了3-PRS并聯機構的工作空間;LI等[15]對3-PRS使用數值搜索方法對并聯機構的可達工作空間進行了分析。上述大部分2T1R并聯機構很少具有運動解耦性[16-18]及符號式位置正解[19-20],使得機構運動學建模以及誤差分析、剛度分析以及動力學分析等方面較為困難,計算量大。

機構動力學分析方法中,拉格朗日法[21-22]通過動能及勢能推導來建立動力學方程,其表現形式相對簡單,但在解決多桿件機構時計算量較大;牛頓-歐拉法[23]將待分析機構拆分開,建立相對應完整的動力學模型,對于構件較多的機構,分析較繁瑣、計算量大;而虛功原理法[24-25]通過系統的虛位移做功建立機構動力學模型,只需要計算較少速度矩陣,具有高效、便捷的特點。基于虛功原理的力分析序單開鏈法[26]能求出驅動副反力(矩)外,還能求解出機構運動副中的作用力。

本文根據基于方位特征方程(POC)的并聯機構拓撲設計理論方法[11],設計兩種零耦合度的2T1R并聯機構,它們具有相同運動副類型和數目,但在支鏈中的分布順序不同,對這兩種機構的主要拓撲特性(POC集、自由度、耦合度)進行分析;根據基于拓撲特征的運動學建模方法,求解兩種并聯機構的位置正反解;基于位置正解求解各自的工作空間與奇異性;又根據基于雅可比矩陣求解兩種并聯機構動平臺中心點的速度與加速度曲線,根據基于虛功原理的力分析序單開鏈法對兩種機構進行動力學建模,求解各自的驅動力;對比分析兩種新型機構的運動學、動力學性能,得到其一為優選機構,并給出優選機構應用場景的概念設計。

1 機構設計和分析

1.1 機構設計

1.1.1支鏈設計

機構動平臺POC集計算式[11,24]為

(1)

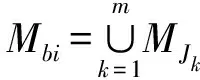
(2)

式中MJk——第i個運動副POC集

Mbi——第i條支鏈末端POC集

MPa——機構動平臺POC集

(1)混合支鏈Ⅰ設計

2-DOF的兩滑塊平面五桿機構(P1⊥R11‖R12‖R13⊥P2)如圖1a所示。為便于闡述,在靜平臺0上建立坐標系oxyz,x軸方向平行于P1軸線方向,y軸方向垂直于P1軸線方向,z軸方向平行于靜平臺0法線方向。取R12軸線上一點為基點,顯然,其末端構件能夠產生平行于xoz平面的兩維移動(2T)以及平行于y軸的一維轉動(1R),即其POC為2T1R。

圖1 兩種混合支鏈

由式(1)可得,該子并聯機構末端輸出的POC集為

在子并聯機構的輸出轉動副R12的輸出軸上串聯一個與其同軸線的轉動副R3,即轉動副R12與R3是復合鉸鏈,再在垂直于R3的軸線上串聯一個轉動副R4(即R4⊥R3);且用轉動副R4連接動平臺1的一端,從而得到混合支鏈Ⅰ1(圖1b)。

在子并聯機構輸出轉動副R12的輸出軸上串聯一個與其同軸線的轉動副R3,即轉動副R12與R3是復合鉸鏈;再在垂直于R3的軸線上串聯一個軸線相平行的轉動副組R4、R5(即R4⊥R3),且R4‖R5,且用轉動副R5連接動平臺1的一端,從而得到混合支鏈Ⅰ2(圖1c)。

由式(2)可知,混合支鏈Ⅰ1、Ⅰ2上末端轉動副R4、R5軸線上一點的POC集分別為

(3)

(4)

式(3)表明,混合支鏈Ⅰ1末端的輸出運動為xoz平面內的兩維移動(2T)以及繞轉動副R4、R12軸線的兩維轉動(2R);式(4)表明,混合支鏈Ⅰ2末端的輸出運動為三維移動(3T)以及繞轉動副R5、R12軸線的兩維轉動(2R),因設計目的是兩平移一轉動,故需設計另一條約束支鏈來分別約束支鏈Ⅰ中多余的運動元素,以滿足其設計目標。

(2)混合支鏈Ⅱ設計

為使機構具有較好的承載能力及剛度,混合支鏈Ⅱ采用包含由4個轉動副組成的平行四邊形機構(簡稱:Pa機構),且至少包含2T1R運動元素的支鏈結構。

將移動副P3與Pa機構一短邊串聯的轉動副R5剛性連接,且移動副P3的軸線與轉動副R5相互平行;又在該Pa機構對邊短桿上串聯另一個轉動副R6,使轉動副R6與動平臺1另一端連接,這樣,組成另外一條混合支鏈Ⅱ1。因此,混合支鏈Ⅱ1可記作{-P3‖R5(-Pa)‖R6-},如圖2a所示。

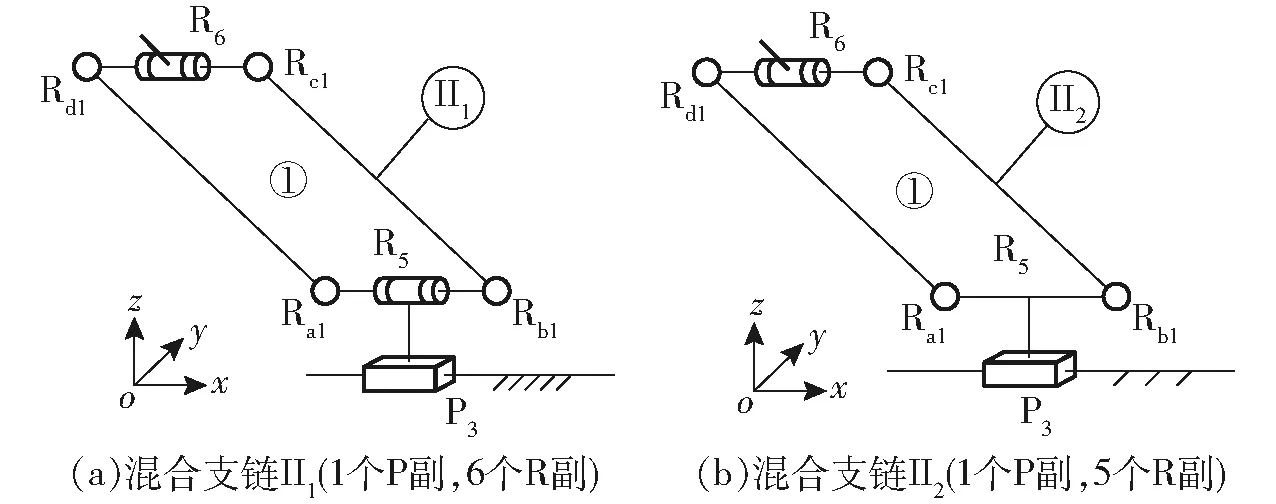
圖2 混合支鏈Ⅱ的設計

同樣,將移動副P3與Pa機構的一條短邊平行且剛性連接,在Pa機構的另一邊短桿再串聯轉動副R6,使轉動副R6的軸線與R5相互平行布置,且用轉動副R6連接動平臺1的另一端,從而組成混合支鏈Ⅱ2。因此,混合支鏈Ⅱ2可記作{-P3(-Pa)‖R6-},如圖2b所示。

對于混合支鏈Ⅱ1,由式(2)可知,混合支鏈Ⅱ1末端構件上R6軸線外任一點的POC集為

M3=MP3∪MPa∪MR5∪MR6=

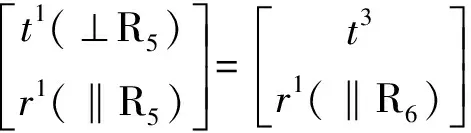
因此,混合支鏈Ⅱ1末端構件能夠產生三維移動(3T)和平行于轉動副R6的一維轉動(1R)。

對于混合支鏈Ⅱ2,由式(2)可知,混合支鏈Ⅱ2末端構件上R6軸線上任一點的POC集為

M4=MP3∪MPa∪MR6=

因此,混合支鏈Ⅱ2末端構件能夠產生平行于xoz平面的二維移動(2T)和平行于轉動副R6的一維轉動(1R)。

1.1.2機構構成

使混合支鏈Ⅰ1中的移動副P1、P2與混合支鏈Ⅱ1中的P3平行布置,且將設計的混合支鏈Ⅰ1與混合支鏈Ⅱ1相互配合,混合支鏈Ⅰ2與混合支鏈Ⅱ2組合,分別并行地連接于靜平臺0與動平臺1之間,得到的機構A與機構B如圖3所示。機構A動平臺前端轉動副R4在Y向的位置不變,而機構B動平臺后端轉動副R6在Y向的位置不變。混合支鏈Ⅰ都含有五桿機構,混合支鏈Ⅱ都含有Pa機構,但其支鏈拓撲結構的局部稍有不同,而運動副類型及總數均相同。

圖3 兩種2T1R并聯機構

根據式(1)可知,2T1R并聯機構A動平臺1上R4軸線上一點的POC集為

MPa1=M1∩M3=

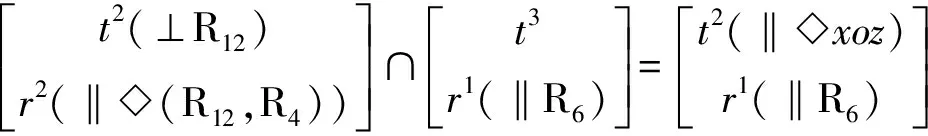
同樣,2T1R并聯機構B動平臺1上R6軸線上一點的POC集為

MPa2=M2∩M4=

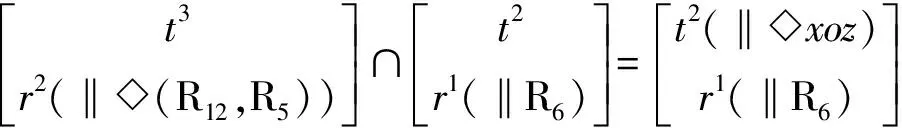
1.2 機構自由度計算

機構全周自由度計算公式[11,24]為

(5)

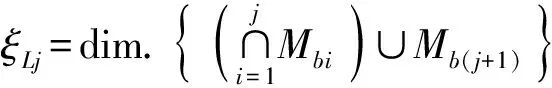
(6)

v=m-n+1

式中F——機構自由度

fi——第i個運動副的自由度(不含局部自由度)

m——機構所含的運動副數

v——獨立回路數

n——機構所含的構件數

ξLj——第j個回路的獨立位移方程數

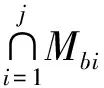
Mb(j+1)——第j+1條支鏈末端構件的POC集

對機構A、B而言,顯然,第1條回路為平面五桿機構(子并聯機構),易知,其獨立位移方程數ξL1為3,由式(5)可知,該子并聯機構自由度為

而第2回路有所不同,對于并聯機構A,第2回路由上述子并聯機構、轉動副組(R3⊥R4)與混合支鏈Ⅱ1{-P3‖R5(-Pa)‖R6-}構成,其獨立位移方程數ξL2由式(6)計算為

ξL2=

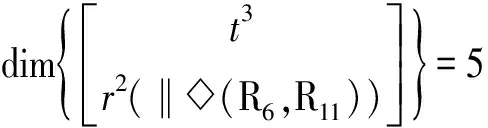
故并聯機構A的自由度F2由式(5)計算為

對于并聯機構B,第2回路由上述子并聯機構、轉動副組(R3⊥R4‖R5)與混合支鏈Ⅱ2{-P3(-Pa)‖R6-}構成,其獨立位移方程數ξL3由式(6)計算為

故并聯機構B自由度F1由式(5)計算為

機構自由度為3,因此,當取靜平臺0上的移動副P1、P2、P3為驅動副時,動平臺1可以實現xoz平面的兩維移動和繞轉動副R4軸線的一維轉動的輸出運動。

1.3 耦合度計算

由基于單開鏈(SOC)組成原理[11]可知,任何一個機構都可分解為約束度為正、零、負的3種有序單開鏈(SOC),第j個SOCj的約束度[11,18]為

(7)

式中mj——第j個SOCj的運動副數

Ij——第j個SOCj的驅動副數

一組有序的v個SOC可劃分為若干個最小的子運動鏈SKC,每個SKC僅含一個自由度為零的基本運動鏈(BKC),SKC的耦合度κ,其計算式為

(8)

對于并聯機構A,其兩個回路的SOC約束度由式(7)分別計算為

由SKC的判定準則[11,24]可知,并聯機構A包含有2個SKC,其中,SKC1為P1⊥R11‖R12‖R13⊥P2,SKC2為R3⊥R4‖R6‖Pa‖R5‖P3,其耦合度由式(8)計算為

而對于并聯機構B,兩個回路的SOC約束度由式(7)分別計算為

由SKC的判定準則[11,24]可知,并聯機構B包含有2個SKC,其中,SKC1為P1⊥R11‖R12‖R13⊥P2,SKC2為R3⊥R4‖R5‖R6‖Pa‖P3,其耦合度由式(8)計算為

表明兩種機構均只包含2個SKC,其耦合度κ為0,因此,機構符號式位置正解可由獨立求解2個SKC而得。

1.4 運動解耦性與基于SKC的機構拓撲解析

并聯機構A、B的拓撲結構解析式[18]可表示為

(9)

(10)

對上述兩種并聯機構的拓撲分析表明:這兩個機構的動平臺均可實現xoz運動平面內的兩維移動(2T)以及繞x軸(平行于轉動副R4軸線)的一維轉動,其自由度均為3。這兩個機構的耦合度為零,進而無須設定虛擬變量,可直接求解得出其位置正解。動平臺基點(對機構A而言為R4,對機構B而言為R6)在y軸方向的位置分量為定值。并聯機構A在xoz平面內x軸方向和z軸方向的兩維移動(x、z)由SKC1中的移動副P1、P2決定,機構A的轉動角由移動副P1、P2、P3共同決定;并聯機構B在xoz平面內x軸方向的一維移動(x)由SKC1中的移動副P1、P2決定,而在xoz平面內z軸方向的一維移動以及轉動角由移動副P1、P2、P3共同決定;因此,并聯機構A具有較好的部分運動解耦性。

2 并聯機構運動學分析

2.1 位置分析

2.1.1機構A正逆解分析

機構A的運動學模型如圖4所示,其位置正解求解歸納為:已知求驅動副輸入量x1、x2、x3,求動平臺1基點位置O′(x,y,z)及姿態角α。

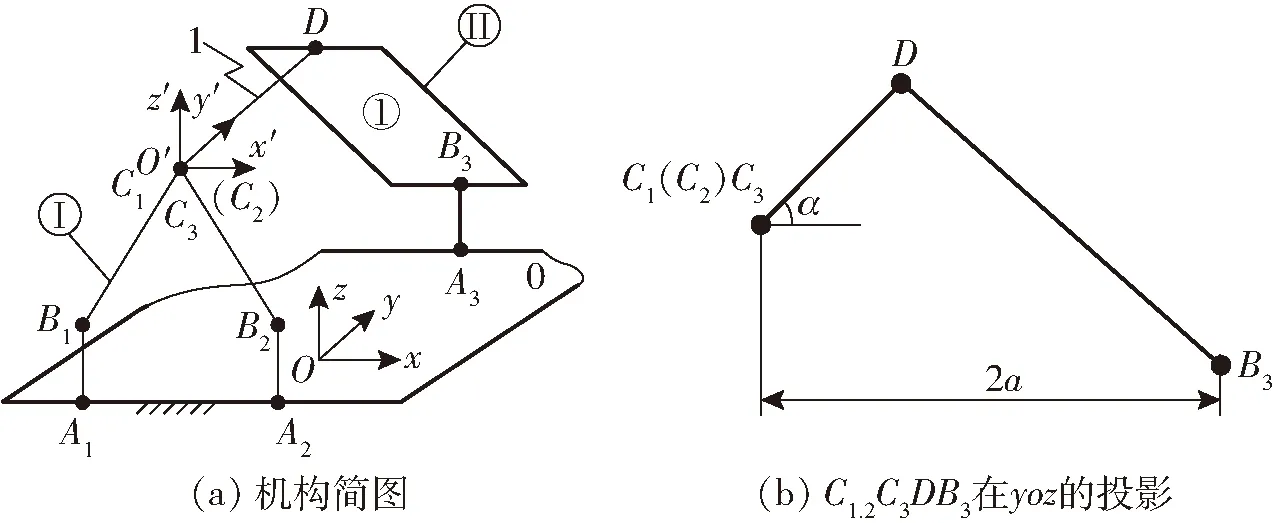
圖4 并聯機構A運動學建模

設靜平臺0兩導軌之間的距離為2a,靜坐標系Oxyz原點O位于兩導軌的幾何中心處,x軸平行于A1A2,y軸垂直于A1A2,z軸由右手螺旋法則確定。在動平臺1中轉動副R4(圖4a中點C3)的中心建立O′x′y′z′坐標系,x′軸與靜坐標系x軸平行且方向一致,y′軸與靜坐標系y軸平行且方向一致,z′軸與靜坐標系z軸平行且方向一致。

設A1B1=A2B2=A3B3=l1,B1C1=B2C2=l2,C3D=l3,DB3=l4,動平臺姿態角為α,如圖4b所示。

(11)

該機構中C1、2、3D∈B3在yoz面的投影,如圖4b所示。

因此,可以得到

(12)

由桿長約束條件DB3=l4,可得

(13)

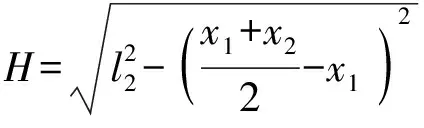
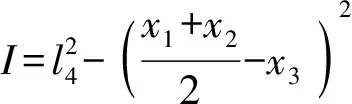
N1=2Hl3N2=-4al3

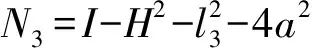
式(13)中m=±1,所以正解數目為2×1=2。

而機構的位置逆解求解可歸納為:已知動平臺1的位置O′及姿態角α,求驅動副輸入量x1、x2、x3。

由桿長約束條件DB3=l4及位置正解,可得

(v=±1)

(14)

由于式(14)中u=±1,v=±1,所以正解數目為2×2=4。

2.1.2機構B正逆解分析

機構B運動學模型如圖5所示。

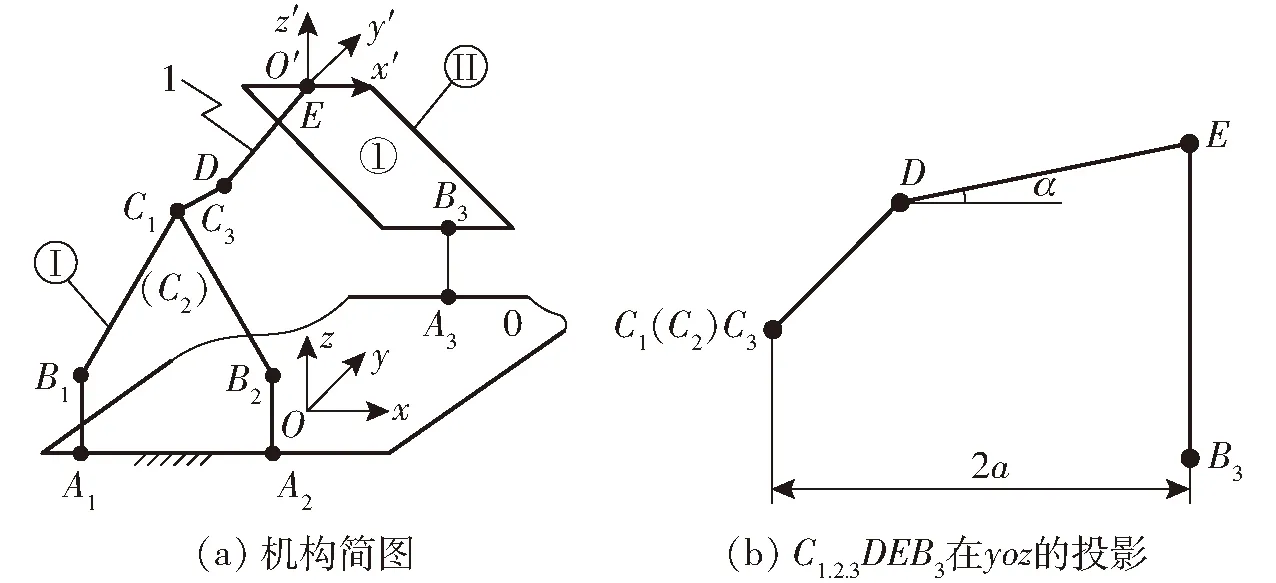
圖5 并聯機構B運動學建模

機構B靜坐標Oxyz建立同機構A。在動平臺1中轉動副R6(圖5a中點C3)的中心建立O′x′y′z′坐標系,x′軸與靜坐標系x軸平行且方向一致,y′軸與靜坐標系y軸平行且方向一致,z′軸與靜坐標系z軸平行且方向一致。

設A1B1=A2B2=A3B3=l1,B1C1=B2C2=l2,C3D=l3,DE=l4,EB3=l5,動平臺姿態角為α,如圖5b所示。

由桿長約束條件DE=l4,可得

(15)

其中

N1=4al4N2=2Jl4

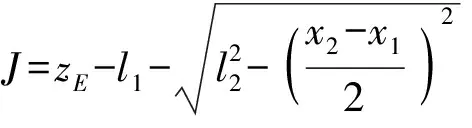
由于式(15)中m=±1,n=±1,因此正解數目為2×2=4。

進一步,逆解可由位置正解得

(16)

其中

(w=±1)

(17)

由于式(16)、(17)中u=±1,v=±1,w=±1,因此反解數目為2×2×2=8。

2.1.3正逆解驗算

設并聯機構A尺寸參數為:a=300 mm,l1=100 mm,l2=200 mm,l3=450 mm,l4=320 mm。取3個驅動量x1=-106.09 mm,x2=181.67 mm,x3=-70.29 mm。將上述參數代入正解式(12)、(13)得到動平臺的位置正解,如表1所示。

表1 運動學正解的理論計算值

表1中的2組數據對應的構型圖如圖6所示。

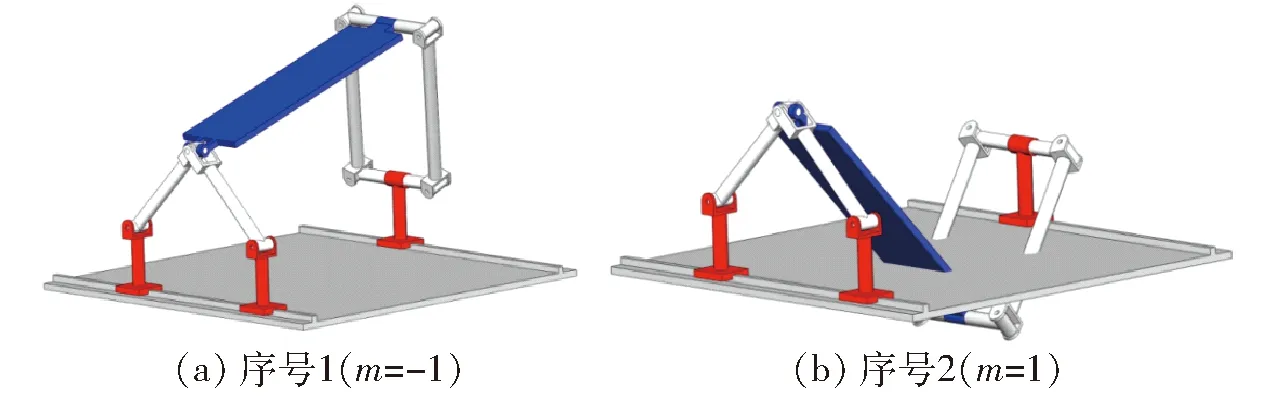
圖6 機構A的正解及其對應的構型

將以圖6a構型(即表1中序號1對應的構型)作為機構A的后續運動學、動力學計算對象。

將在正解中表1中的序號1數值代入式(17),得到的4組反解如表2所示,其所對應4個構型如圖7所示。

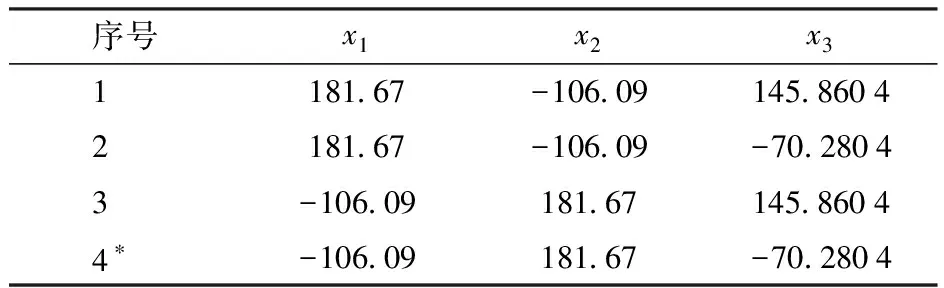
表2 運動學反解的理論計算值

圖7 機構A的反解及其對應的構型

可見,表2中序號4參數與設定的機構輸入參數以及圖6a與圖7d所示構型一致,從而驗證了正逆解公式的正確性。

設并聯機構B的尺寸參數為:a=300 mm,l1=100 mm,l2=200 mm,l3=180 mm,l4=450 mm,l5=320 mm。用同樣的方法,驗證了機構B位置正逆解公式的正確性。

2.2 工作空間

工作空間表示動平臺操作端的運動范圍,是并聯機構的一個重要運動學指標[24-25]。因并聯機構A、B均具有符號位置正解,故采用位置正解來計算工作空間。相比于通過位置逆解及預設工作空間的搜索范圍、搜索所有滿足約束條件的點以形成三維圖的方法,該方法直接搜索驅動副的范圍以確定工作空間,具有計算量少、工作空間計算準確等優點[24]。

2.2.1并聯機構A

確定機構A中3個驅動移動副P1、P2和P3的移動量稍大于機構桿件移動范圍,分別取為-250 mm≤x1≤0 mm,0 mm≤x2≤250 mm,-300 mm≤x3≤300 mm。通過Matlab軟件,對正解式(14)～(16)進行編程,得到該機構動平臺上質心的三維工作空間如圖8a所示;而工作空間xyz中3個不同方向的投影如圖8b～8d所示。

圖8 并聯機構A工作空間及其在xOy、yOz、xOz面的投影

工作空間在x=60 mm、y=-85 mm、z=300 mm平面上的截圖,如圖9所示。

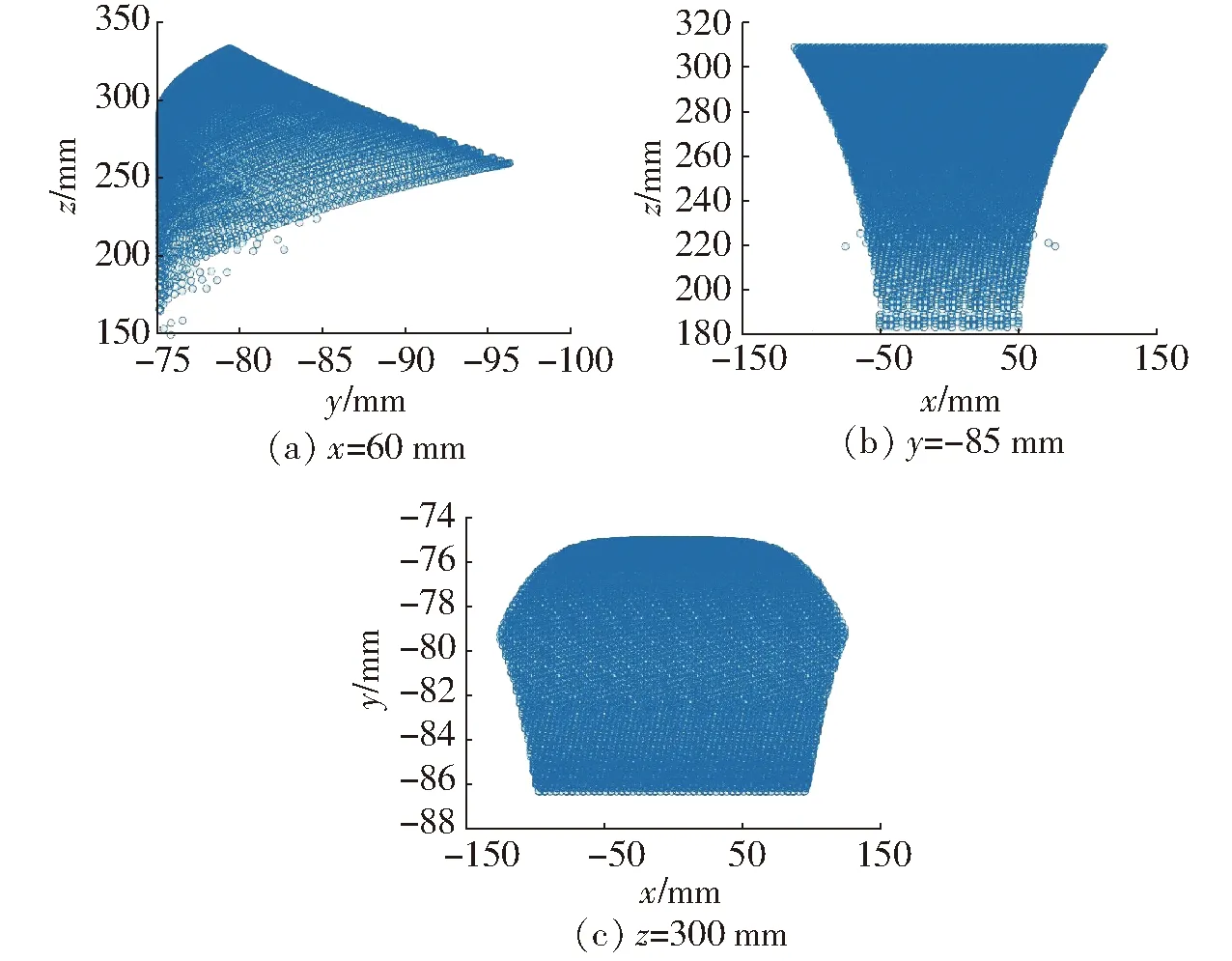
圖9 并聯機構A工作空間內xyz方向上的截面圖

2.2.2并聯機構B

同樣,確定機構B中3個驅動移動副P1、P2和P3的移動范圍同機構A。通過Matlab軟件,對正解式(15)進行編程,得到該機構動平臺上質心的三維工作空間,如圖10a所示;而工作空間xyz3個不同方向的投影,如圖10b～10d所示。

圖10 并聯機構B工作空間及其在xOy、yOz、xOz面的投影

工作空間在x=50 mm、y=213 mm、z=385 mm平面上的截圖,如圖11所示。

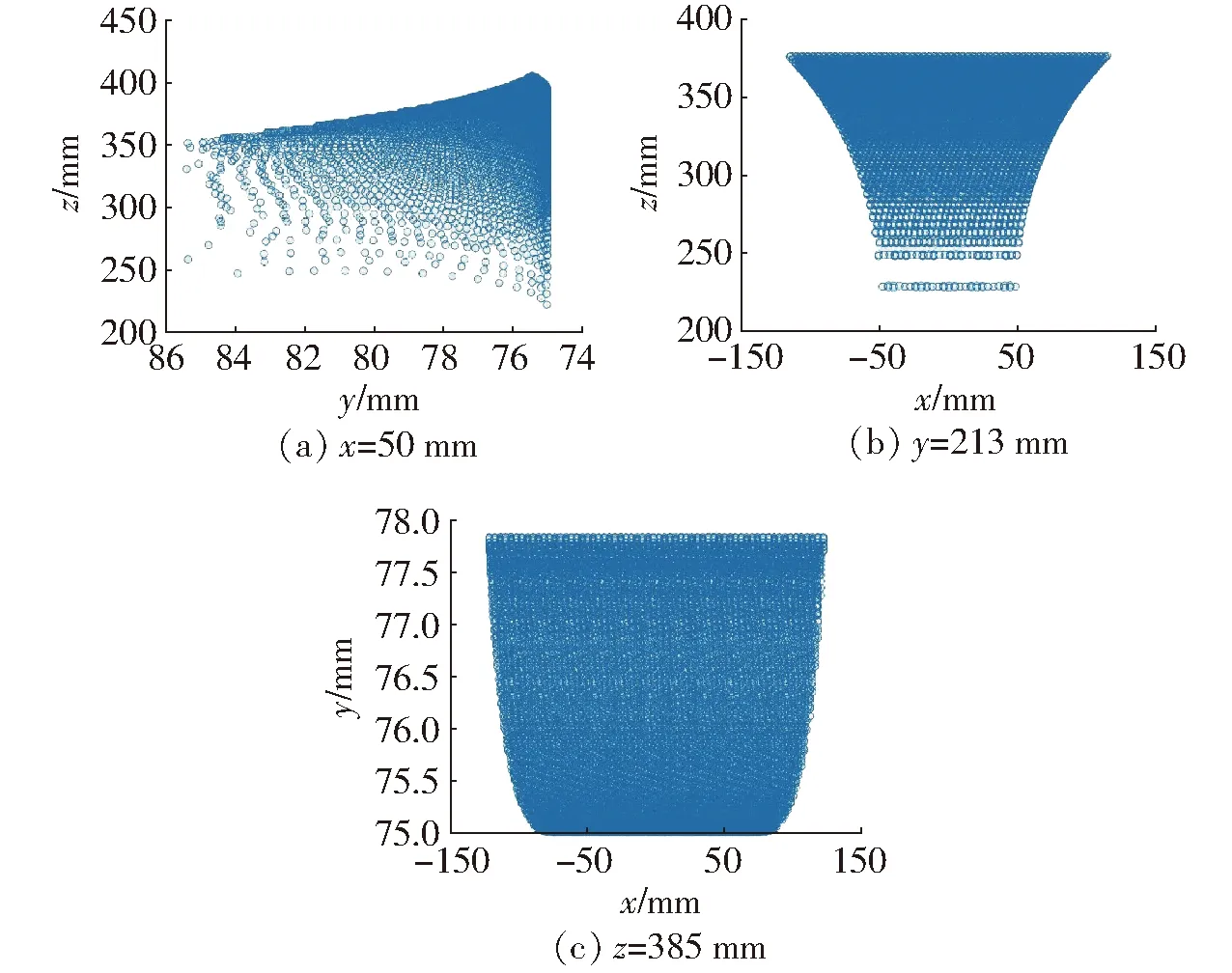
圖11 并聯機構B工作空間內xyz方向上的截面圖

2.3 奇異性分析

采用基于雅可比矩陣的奇異位形及分析方法。雅可比矩陣為[26-27]輸入關節速度到機構末端輸出速度的映射,由于矩陣內部元素與位置有關,該映射關系為

(18)

式中Jo、Ji——輸出、輸入雅可比矩陣

根據Jo和Ji矩陣是否奇異,將機構分為3種奇異類型:①當det(Ji)=0時,機構發生輸入奇異。②當det(Jo)=0時,機構發生輸出奇異。③當det(Ji)=det(Jo)=0時,機構發生綜合奇異。

2.3.1并聯機構A

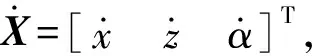
(1)輸入奇異

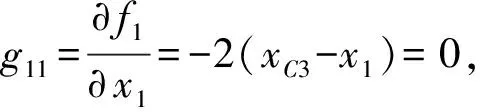
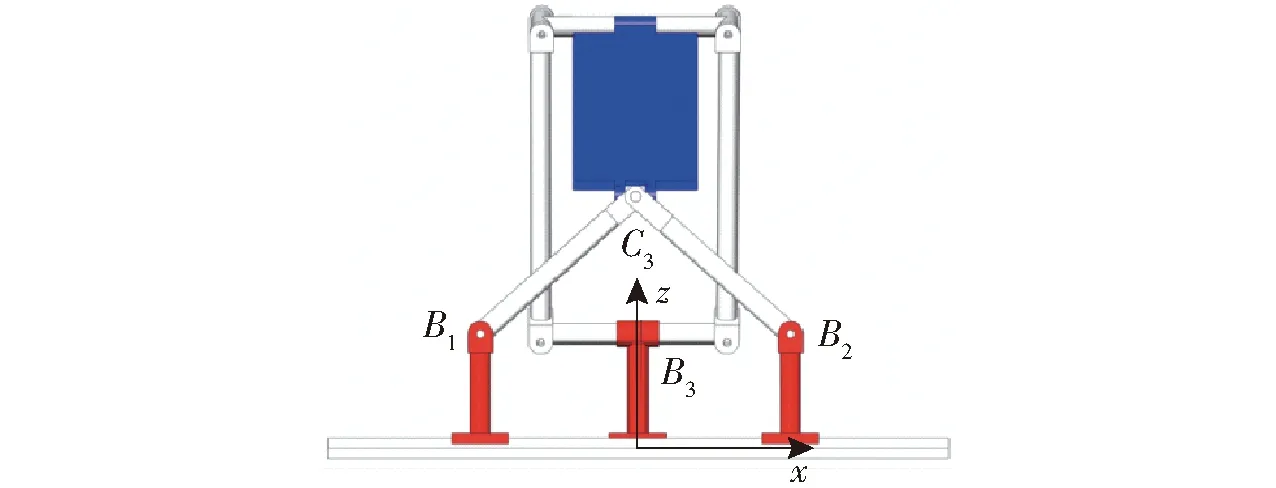
圖12 輸入奇異位置

(2)輸出奇異

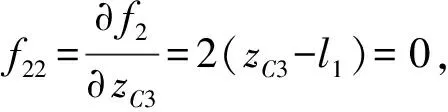
圖13 輸出奇異位置

(3)綜合奇異

當det(Ji)=det(Jo)=0時,即輸入、輸出奇異同時存在,機構才發生綜合奇異,經分析該機構不發生綜合奇異。

2.3.2并聯機構B

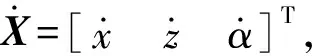
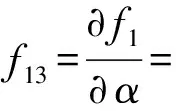
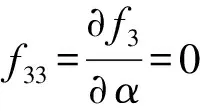
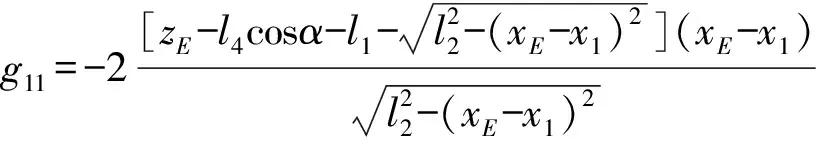
(1)輸入奇異

圖14 輸入奇異位置1

圖15 輸入奇異位置2

(2)輸出奇異

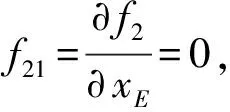
(3)綜合奇異

當det(Ji)=det(Jo)=0時,機構才發生綜合奇異;經分析發現該機構不發生綜合奇異。

3 機構動力學分析

3.1 并聯機構A

因機構A、B的耦合度均為零,因此這兩個機構各桿件的速度和加速度均可由剛體運動學速度(加速度)合成定律求得,其分析計算流程圖如圖16所示。

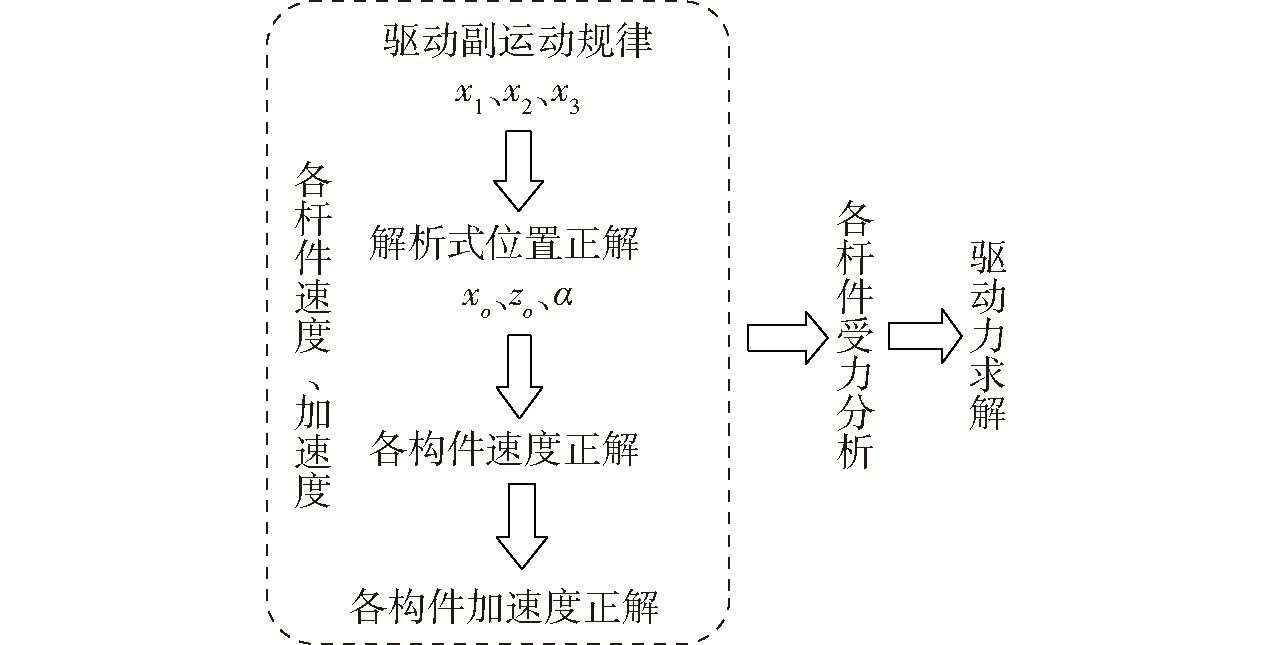
圖16 機構速度、加速度分析流程圖

取3個驅動副P11、P21、P31的輸入函數分別為y1=20sin(πt)、y2=-10sin(πt)、y3=20sin(πt),且3個驅動副的初始位置分別為ρ1=-131.07 mm、ρ2=181.55 mm、ρ3=-57.74 mm。

利用Matlab得到機構A動平臺質心的速度與加速度的理論計算曲線如圖17所示。

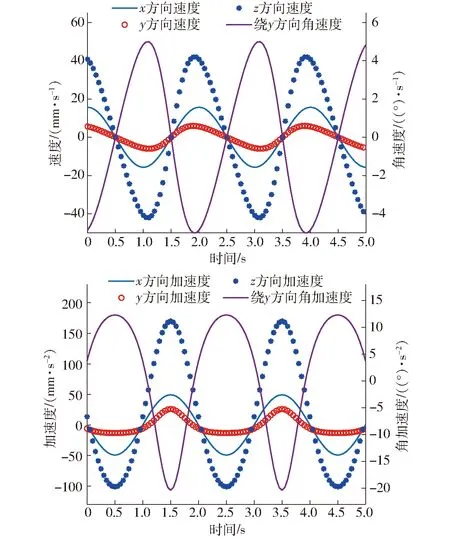
圖17 機構A動平臺質心速度、加速度理論計算曲線

在ADAMS軟件中對虛擬樣機進行仿真,得到機構A動平臺的質心的速度與加速度仿真曲線如圖18所示。

圖18 機構A動平臺質心速度、加速度仿真曲線

3.2 并聯機構B

3個驅動副P11、P21、P31取相同的輸入函數及3個驅動副的初始位置,利用Matlab得到機構B動平臺質心的速度與加速度的理論計算曲線如圖19所示。

圖19 機構B動平臺質心速度、加速度的理論計算曲線

在ADAMS軟件中對虛擬樣機進行仿真,得到機構B動平臺的質心的速度與加速度仿真曲線如圖20所示。

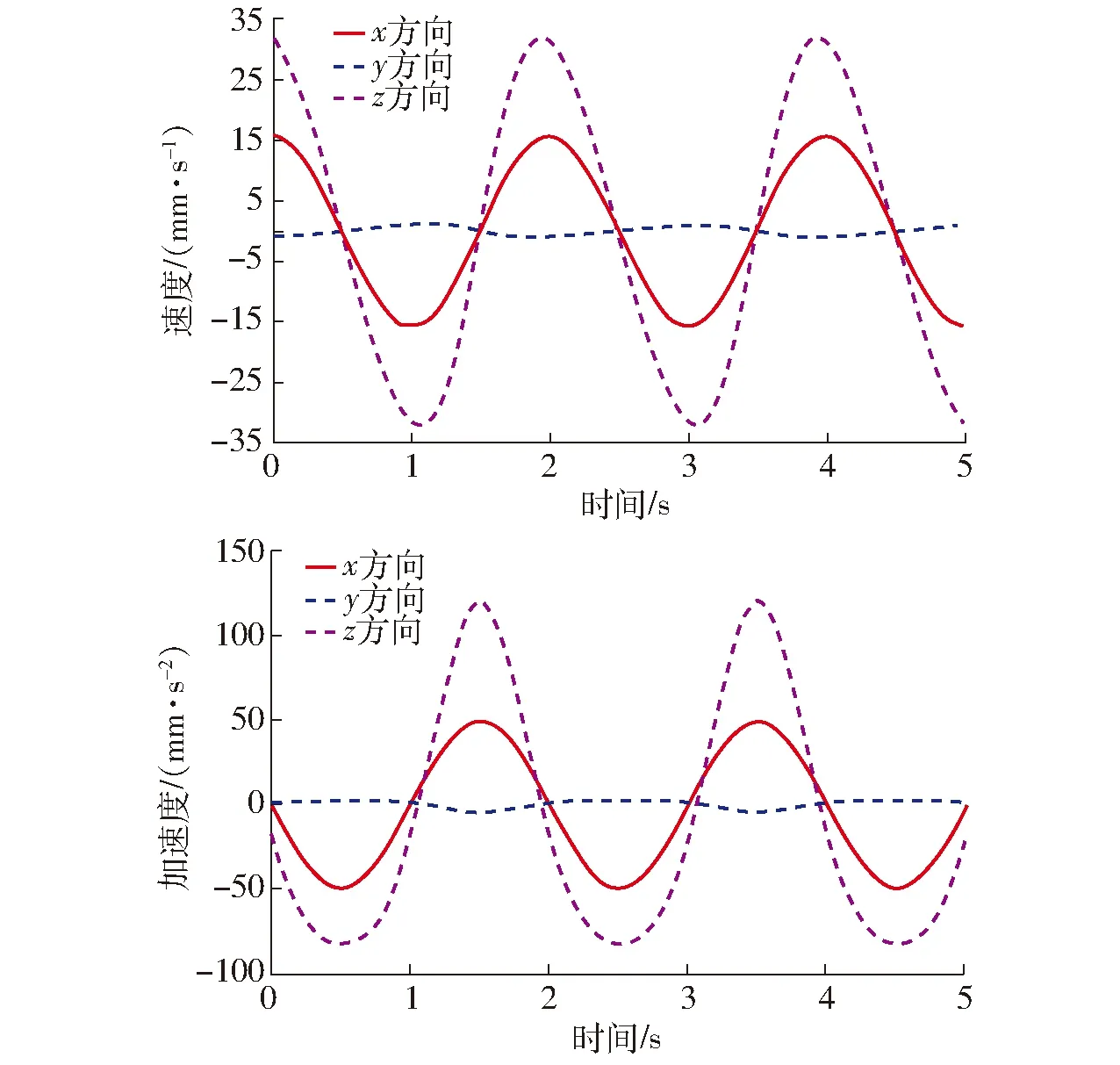
圖20 機構B動平臺質心速度、加速度的仿真曲線

從圖17、18及圖19、20可知,并聯機構A、B理論計算的速度與加速度曲線與ADAMS仿真得到的曲線一致,表明其運動學建模求解的正確性;動平臺1質心的速度與加速度曲線變化平緩,沒有陡增陡減的突變現象發生,表明該機構A、B運動性能良好,均有潛在利用價值。

3.3 機構動力學建模

3.3.1基于虛功原理的力分析序單開鏈法

3.3.1.1并聯機構A

(1)SKC2內各構件受力分析

取動平臺質點為點P,則有

(19)

式中fp——動平臺質心外力

τp——動平臺質心外力矩

mp——動平臺質量

Ip——動平臺慣性矩陣

ε1——動平臺角加速度

ω1——動平臺角速度

a1——動平臺線性速度

g——重力加速度

由驅動副A3B3受力分析可得

(20)

其中

式中f3——驅動副P3驅動力

mA3——驅動副P3質量

aA3——驅動副P3加速度

由轉動桿DB3受力分析可得

(21)

式中mDB3——轉動桿DB3質量

IDB3——轉動桿DB3慣性矩陣

(2)SKC1內各構件受力分析

由驅動副AiBi受力分析可得

(i=1,2)

(22)

式中fi——驅動副AiBi驅動力

mAiBi——驅動副AiBi質量

aAiBi——驅動副AiBi加速度

由轉動桿BjCj受力分析可得

(j=1,2)

(23)

式中mBjCj——轉動桿BjCj質量

IBjCj——轉動桿BjCj慣性矩陣

3.3.1.2并聯機構B

(1)SKC2內各構件受力分析

取動平臺質點為點P,則有

(24)

由驅動副A3B3受力分析可得

(25)

由轉動桿DB3受力分析可得

(26)

(2)SKC1內各構件受力分析

由驅動副AiBi受力分析可得

(27)

由轉動桿BjCj受力分析可得

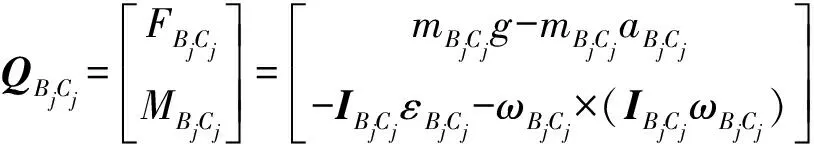
(j=1,2)

(28)

由轉動桿C3D受力分析可得

(29)

式中mC3D——轉動桿C3D質量

IC3D——轉動桿C3D慣性矩陣

3.3.2動力學方程建立

3.3.2.1并聯機構A

解除兩個SKC在點C3的運動副約束之后,支反力FC3轉化為未知外力,根據基于虛功原理的力分析序單開鏈法分別建立SKC1、SKC2動力學方程為

(30)

(31)

其中

δxAiBi=JvAiBiδq(i=1、2、3)

δxBjCj=JvBjCjδq(j=1、2)

δxDB3=JvDB3δqδxp=JvpδqδxDC3=JvDC3δq

δθB1C1=JωB1C1δqδθB2C2=JωB2C2δq

δθp=JωpδqδθDB3=JωDB3δq

將式(19)～(23)代入式(30)、(31)即可求出兩個SKC連接處點C3處的支反力。

3.3.2.2并聯機構B

解除兩個SKC在點E的運動副約束之后,支反力FC3轉化為未知外力,同樣可建立SKC1、SKC2動力學方程為

(32)

(33)

將式(24)～(29)代入式(32)、(33)即可求出兩個SKC連接處點C3處的支反力。

3.4 機構動力學的驗證與仿真

3.4.1并聯機構A

設機構A中各桿件的質量分別為:mA1B1=0.056 93 kg;mA2B2=0.056 93 kg;mA3B3=0.067 27 kg;mB1C1=0.072 01 kg;mB2C2=0.070 42 kg;mC3D=0.494 4 kg;mDB3=0.105 86 kg;mRaRb=0.071 83 kg;mRcRd=0.062 41 kg。各桿件轉動慣量如表3所示。

表3 機構A各桿件轉動慣量

將上述參數代入動力學方程式(19)～(23),取3.1節(忽略摩擦時)該機構在負載5 kg(fp=50 N,τp=0)狀態下的驅動力,如圖21所示。

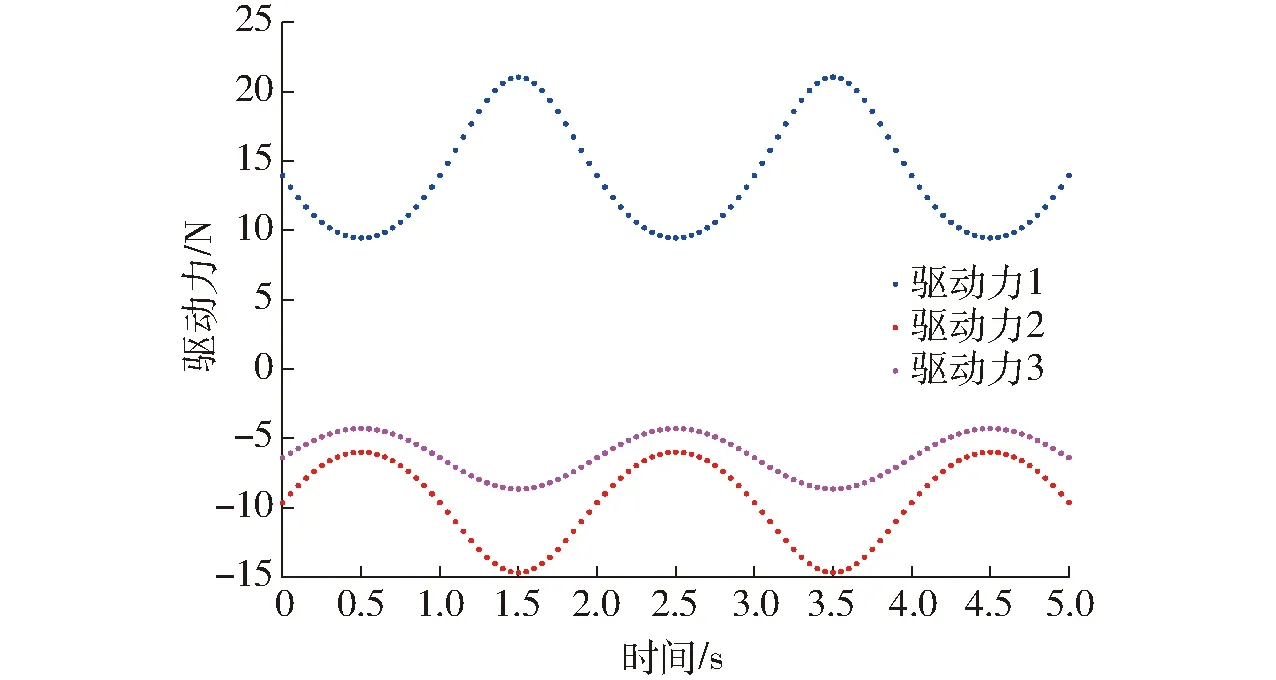
圖21 并聯機構A驅動力理論曲線

將虛擬樣機導入ADAMS中,選取運動仿真時間為5 s,得到的驅動力仿真曲線如圖22所示。

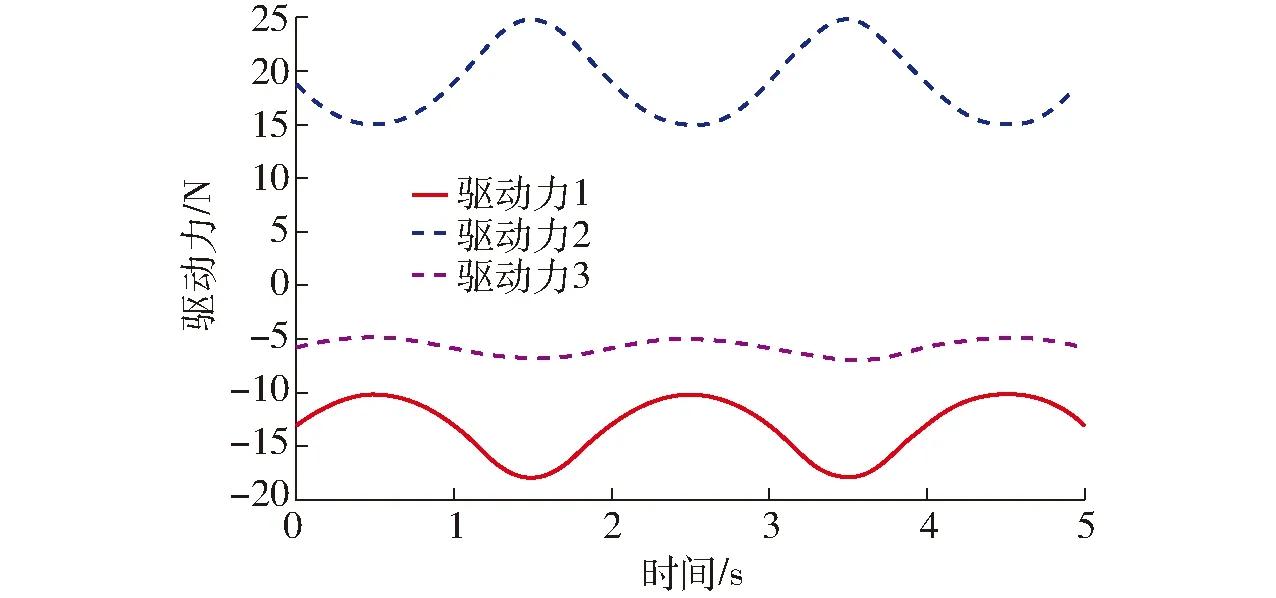
圖22 并聯機構A驅動力仿真曲線

3.4.2并聯機構B

設機構B中各桿件的質量分別為:mA1B1=0.056 93 kg;mA2B2=0.056 93 kg;mA3B3=0.124 90 kg;mB1C1=0.072 01 kg;mB2C2=0.070 42 kg;mC3D=0.494 4 kg;mDE=0.494 4 kg;mRaRb=0.105 67 kg;mRcRd=0.063 78 kg。各桿件轉動慣量如表4所示。

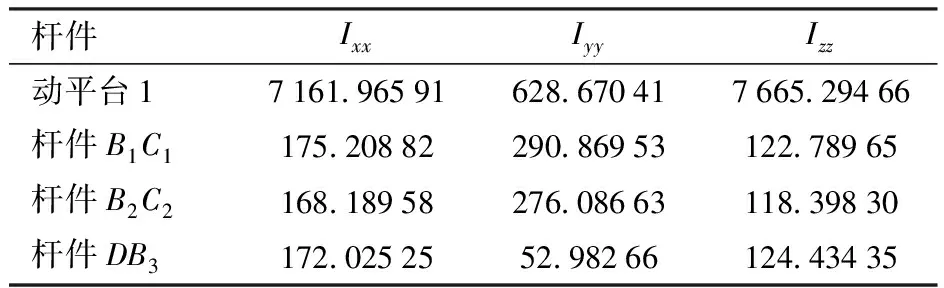
表4 機構B各桿件轉動慣量

將上述參數代入動力學方程式(24)～(29),取3.2節的輸入函數作為驅動副的輸入函數,運用Matlab計算(忽略摩擦時)該機構在負載5 kg(fp=50 N,τp=0)狀態下運動副處的驅動力,如圖23所示。

圖23 并聯機構B驅動力理論曲線

同時,將虛擬樣機導入ADAMS 中,選取運動仿真時間為5 s,得到的驅動力仿真曲線如圖24所示。

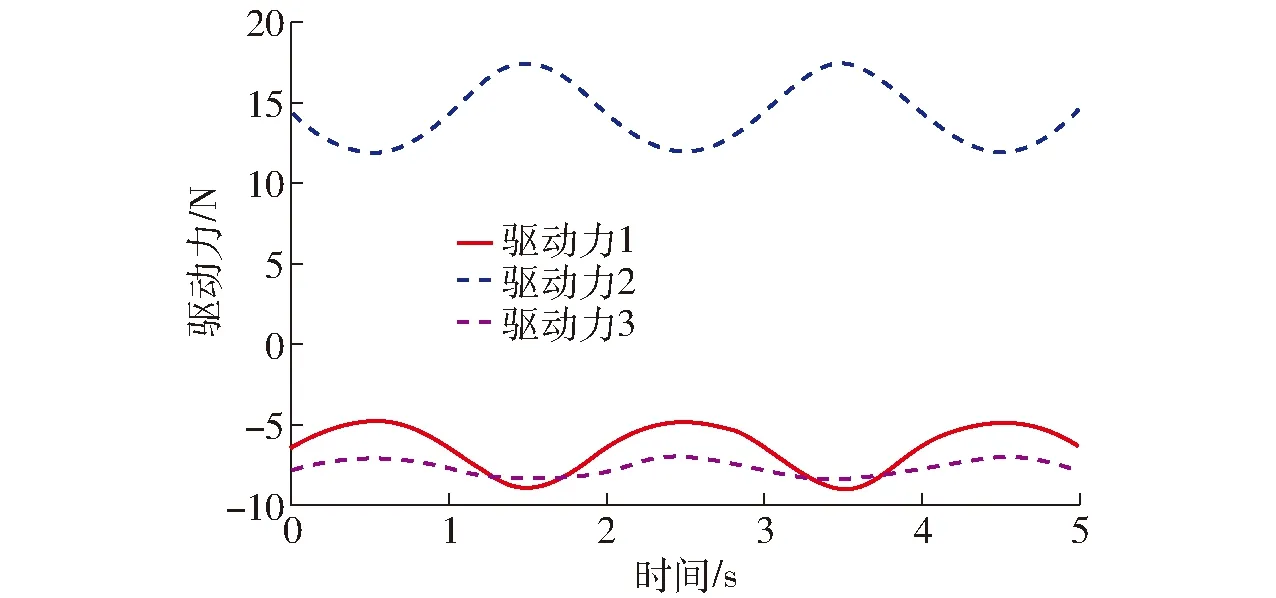
圖24 并聯機構B驅動力仿真曲線

對比圖21、22以及圖23、24易知,驅動力理論計算曲線與ADAMS仿真曲線基本一致,即兩種機構動力學模型是正確的,僅存在微小差距,其主要原因在于:各運動副連接處存在間隙,理論計算的參數值與實際模型的參數值有差距;以及ADAMS軟件仿真是基于 Lagrange方程建立的動力學仿真模型,而本文主要采用基于虛功原理的序單開鏈法,在計算時存在舍入誤差和累計誤差。

4 應用場景概念設計

將設計的2T1R機構A應用于水果深加工的智能分揀、傳送工藝中,其應用場景概念設計三維圖如圖25a所示,工作平面示意圖如圖25b所示,空間結構布置簡圖如圖25c所示。其工作原理是:

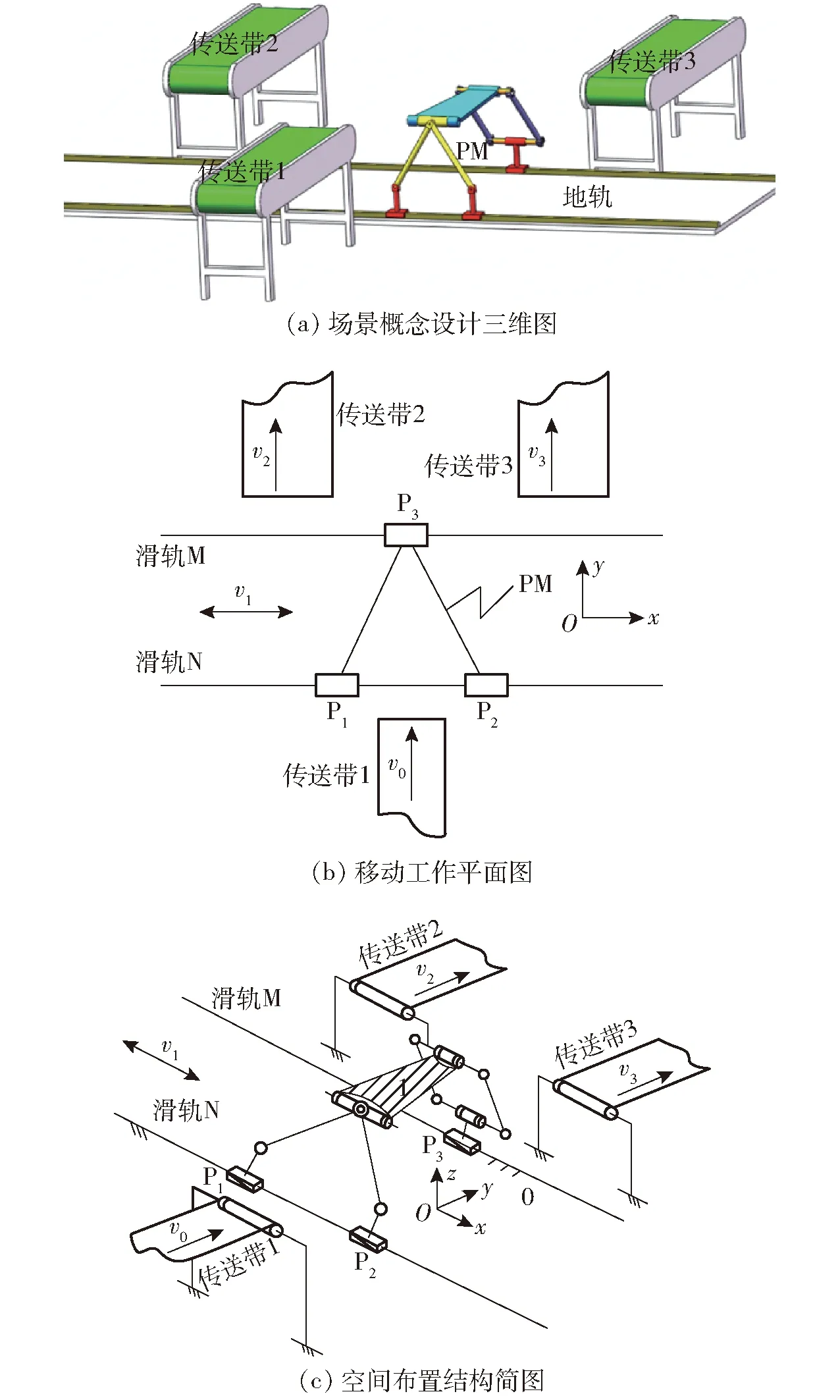
圖25 應用場景的概念設計

(1)傳送帶1以速度v0將等待分揀加工的裝筐蘋果送至指定位置,2T1R并聯機構在傳送帶1的末端等待承接蘋果,通過掃描識別裝筐蘋果的品質標簽,以速度v1進行運輸,待運輸到相對應品質的生產線時,并聯機構通過動平臺的斜坡將裝筐蘋果滑動到下一環節的傳送帶上。①品質略有瑕疵的裝筐蘋果通過動平臺轉運到傳動帶2上,以速度v2進入蘋果深加工車間。②品質較好的裝筐蘋果通過動平臺轉運到傳送帶3上,以速度v3進入封裝出貨車間。

(2)當導軌上的驅動移動副P1、P2、P3取相同速度大小和方向時,可實現長距離的移動,以使傳送帶1上的裝筐蘋果通過傳送帶2將瑕疵蘋果或通過傳送帶3將高品質蘋果送至相應的庫存或相應環節進一步的加工。

(3)當導軌上的驅動移動副P1、P2、P3取不同速度大小和方向時,動平臺可實現xOz平面內的二維移動和繞轉動副R4的一維轉動,其中,x軸方向和z軸方向的移動由P1、P2決定(可以調節動平臺x、z位置),而轉動角的轉動由P1、P2、P3共同決定(可以使動平臺與傳送帶2、3之間位置對應一致,并在y軸方向上靠近傳送帶1、2、3)。

5 結論

(1)根據基于方位特征(POC)方程的并聯機構拓撲結構設計理論與方法,設計兩種零耦合度且部分運動解耦的(2T1R)并聯機構,它們具有相同運動副類型和數目,但在支鏈中的分布順序不同;分別對兩種機構的自由度、耦合度等主要拓撲特性進行分析,結果表明這兩種機構耦合度為零。

(2)根據拓撲特征運動學分析方法對兩個機構進行了運動學建模,驗證了機構具有符號式位置正解;且均具有部分運動解耦性,但機構A部分運動解耦程度更好;分析了這兩種機構的工作空間及其奇異位置,表明機構A在相同的桿長和工作范圍條件下,工作空間更大。

(3)求解了兩種并聯機構動平臺中心點的速度與加速度曲線,表明這兩種機構動平臺質心的速度與加速度曲線變化平緩,沒有陡增陡減的突變現象發生,具有良好的機構運動性能;同時根據基于序單開鏈虛功原理對該機構進行逆向動力學建模,并求得其驅動力變化幅度相似且平緩,表明這兩種機構在實際應用中電機選型的多樣性。

(4)不同運動副分布順序對并聯機構運動學與動力學性能有較大影響;機構A的運動解耦性更好、工作空間更大,因此,選取機構A為優選機構;同時,對機構A用作水果深加工中智能分揀、傳遞的應用場景進行了概念設計。