基于差分進化算法的微電網小水電PID參數優化研究

汪若涵，莊原，朱藝超，和治翔

（1.云南電網有限責任公司昆明供電局，云南 昆明 650011；2.云南電網有限責任公司曲靖供電局，云南 曲靖 655100；3.云南電網有限責任公司大理供電局，云南 大理 671000；4.云南電網有限責任公司迪慶供電局，云南 迪慶 674400）

0 前言

隨著新型電力系統建設，大量分布式光伏、儲能等接入配電網，配電網的能量供給發生巨大的變化，在大電網故障情況下，分布式光伏、儲能、小水電組成水、光、儲微電網穩定運行，可有效提升配電網的供電可靠性。該類微電網穩定運行需要小水電機組有良好的調節性能。而小水電機組調速系統模型參數的準確性直接影響控制器設計，進而影響微電網內機組動態調節特性和微電網的安全穩定[1]。近年來智能算法在函數優化、參數識別等方面表現出一定的優越性，逐步應用于實際工程中。文獻[2]提出一種基于粒子群優化算法的小水電PID 控制器參數優化方法，文獻[3]提出一種基于差分進化算法的FMS 中機器與AGV 同時調度方法，但上述方法僅用于理論研究，工程實際應用不足。其中，差分進化（DE）算法在發電機參數識別方面產生了一些工程應用案例，但仿真分析和現場實測高效結合還有待提升。因此，如何基于工程實際構建較好的智能算法優化模型，提升模型適應性是工程建設人員今后需考慮的方向。

1 差分進化算法

1.1 標準差分進化算法

差分進化（DE）算法通過種群內個體間的相互合作與競爭而決定尋優方向，其進化流程與遺傳算法非常類似[4]，主要優化步驟如下：

1）初始化種群

在搜索范圍內按下式隨機產生最初種群。

式中，i=1,2,...；Xi,j(0)為初始種群中的第i個個體，xLi,j為個體的下邊界，xUi,j為個體的上邊界。

2）變異操作

在此階段通過差分策略實現個體變異,即隨機選取種群中兩個不同的個體,將其向量差乘以一個系數后與待變異個體進行向量相加。

3）交叉操作

對于第代種群中的每一個個體與變異個體進行交叉操作，產生新個體。

4）選擇操作

使經過變異與交叉操作后的新個體與第t代種群中個體進行競爭，選擇適應度值較優的個體進入下一代。當且僅當新個體的適應度值好于第t代種群中個體時，新個體替換第t代種群中個體，從而被選為子代，否則第t代種群中個體被予以保留到下一代。種群中的每個個體均代表待優化PID 參數的一組可能解，種群內進行從父代到子代間的變異、交叉與選擇操作，循環直到達到最大迭代次數，此時便可獲取整個種群最優個體和其對應的最優適應度值，即最優參數[5]。

1.2 DE算法的改進

DE 算法具有容易實現、收斂速度較快、魯棒性較強等優點，但在實際工程應用中，存在局部搜索性能弱，迭代次數上升后計算時間較長的缺陷。筆者嘗試了對差分進化算法在變異環節和選擇環節進行改進。

通常情況下為了增加收斂速度，DE 算法變異環節的縮放因子H設為常數，這使得后代染色體的多樣性降低。本文嘗試了通過改變DE 算法的評價函數來調節縮放因子H，提高后代的多樣性，以下為H因子的自適應調整公式：

其中，H∈[Hmin,Hmax]，K為增益基準值，Oa和Ob為迭代特征值，Hmin和Hmax分別為H的最小值和最大值（本文設置Hmin=0.01，Hmax=2.2，Oa=Ob=4，K=30）。

在選擇環節考慮了較差后代進入下一次變異的概率，改進的選擇方法如下式所示：

其中，r為(0,1)之間均勻分布的一個隨機數；T為當前迭代次數下的溫度值；Pchoose(off) 表示off迭代次數下的選擇概率；f(ui(off)) 表示off迭代次數下所生成的新解；f(xi(off))表示在off迭代次數下當前染色體的解。

通過實際工程應用發現，改進后的ITAE 評價指標變化區間位于百分數的后兩位，對于實際工程應用支撐不足，故本文僅做理論上的探究，標準DE 算法結合合適的仿真模型即可滿足工程應用參數優化的需求。

2 基于差分進化算法和仿真優化評價的小水電機組調速器PID參數優化

目前，在電網工程應用中，PID 控制器參數優化主要以人工調整為主，該方法不僅費時，而且不能保證控制器的最佳性能，常用的誤差性能指標包括ISE、IAE、ITAE、ISTE 等[6]。

差分進化算法已經廣泛應用于函數優化、神經網絡訓練、模式分類、模糊系統控制以及其他應用領域[7]，本文將使用差分進化算法進行PID 控制器參數的優化設計。通過評價差分進化算法迭代后的適應度函數的數值可判斷種群中各個體的優劣，選擇性能指標較好的積分時間絕對誤差（ITAE）作為適應度函數[8]，以期得到最優的調速系統控制策略。該函數表達式如下：

式中，e(t)為系統誤差，此處為機組轉速變化相對值誤差。

PID 控制器應用廣泛（系統結構如圖1 所示），在仿真水輪機調速系統模塊中的形式如圖2 所示。

圖1 PID控制器系統結構

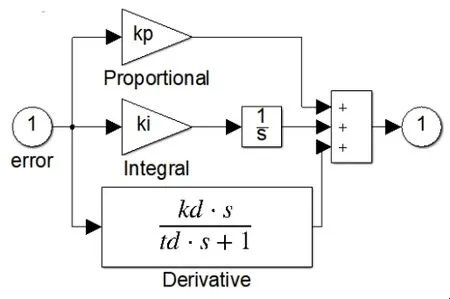
圖2 小水電機組調速系統PID控制圖

其中輸出端口是系統誤差；kp、ki和kd分別是對系統誤差信號及其積分與微分量的加權。PID 控制器的性能取決于、和這3 個參數的合理性[9]。PID 控制器的系統結構圖如圖2 所示。PID 控制器的優化問題就是確定一組合適的參數kp、ki和kd，使得指標達到最優。

在仿真環境下建立的模型如圖3 中，調速系統中的PID 控制器中的微分環節由一個一階環節近似，輸出端頻率由仿真軟件中的yout1d模塊輸出，再由所編寫的m 文件計算得到優化所需要的ITAE 指標。

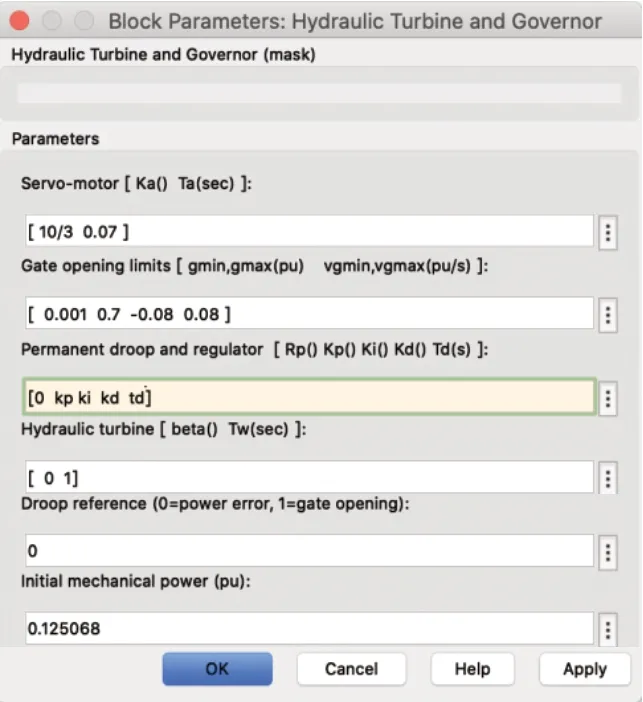
圖3 對模塊進行賦值的界面示意圖

利用差分進化算法對PID 控制器的參數進行優化設計[9]時在水輪機及其調速系統模塊當中的PID 一欄的參數設置為待定參數。

差分進化算法對PID 參數優化的設計過程如圖4 所示。

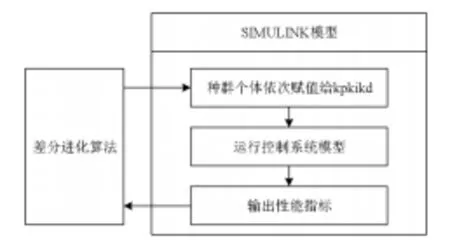
圖4 優化PID的過程示意圖

圖4 中，應用差分進化算法優化更新種群后，依次賦值給PID 控制器的kp、ki和kd參數，然后運行控制系統的仿真評價模型，得到該組參數對應的性能指標，該性能指標傳遞到差分進化算法中作為該粒子的適應值，最后判斷是否可以退出算法[10-11]。

3 基于差分進化算法的PID參數優化仿真

3.1 仿真邊界條件

由于對調速系統參數進行整體優化較為困難，容易陷入局部最優，導致參數尋優過程不理想，因此采用分布優化的方法對兩臺機組的小網控制參數進行優化，實驗總共分為3 步進行，首先對單臺機組進行負荷擾動實驗，對單臺機組調速系統PID 參數進行優化，包括kp、ki、kd、bP，Ef 參數；其次，固定一臺機組參數后再優化另一臺機組的kp、ki、kd、bP，Ef 參數；最后，固定兩臺機組的PID 參數；最后，對進入小網模式的頻率閾值和延時進行優化。

基于軟件進行仿真，迭代次數為100 代。安南電站小水電機組與10 kV 白水臺線組成微電網，小水電機組的仿真參數設置情況如下：kp、ki的取值范圍為[0,1]，kd取值范圍為[0,5]，bP=0。現場小水電站調速系統控制面板參數設置情況如下：T1v 為0.3 s，kp為6，Tw 為1.6s，Ta 為8.2 s，en為1.0，Ky 為0.5。設置4% 的頻率擾動。

3.2 小水電機組PID參數優化仿真

仿真結果如圖5 所示，可以看出DE 算法的性能指標ITAE 不斷減小，PID 控制器的kp、ki、kd參數被不斷的優化，逐步向最優逼近。

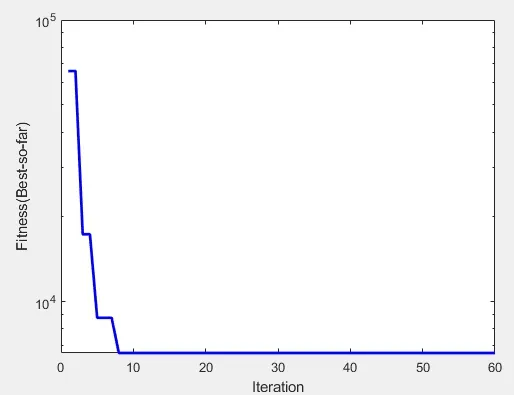
圖5 DE算法適應度曲線

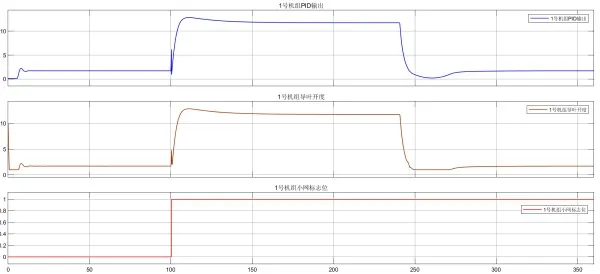
圖6 負荷擾動時1號機組調速系統動作曲線（參數優化前）

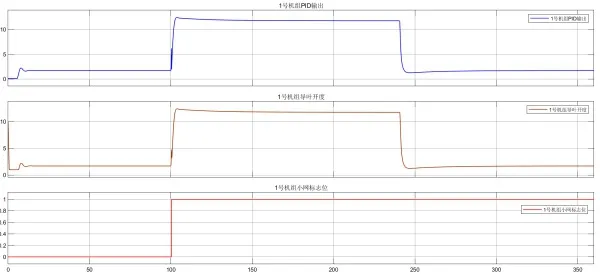
圖7 負荷擾動時1號機組調速系統動作曲線（參數優化后）

由上述結果分析得出，在系統側擾動±300 kW 負荷時，調速系統小網參數優化前，系統最高頻率為52.4 Hz，最低頻率為47.3 Hz，通過DE 算法優化后，同樣在系統側擾動±300 kW 負荷時，系統最高頻率為51.4 Hz，最低頻率為48.5 Hz，故DE 算法對于小網模式PID 參數優化具有較好的效果。優化后的1 號機組調速系統小網PID 參數為kp=2.25、kp=0.8、kd=0.4、bP=0，Ef=±0.3 Hz。

3.3 安南電站小水電機組參數的優化

由安南電站、10 kV 白水臺線組成微電網運行小水電機組進行參數優化及實驗驗證。

基于差分進化算法對調速系統小網PID 參數實測、辨識以及優化后，最終得到1、2 號機組調速系統初始化PID 參數配置表（見表1），用于后續仿真模擬和動態驗證環節。

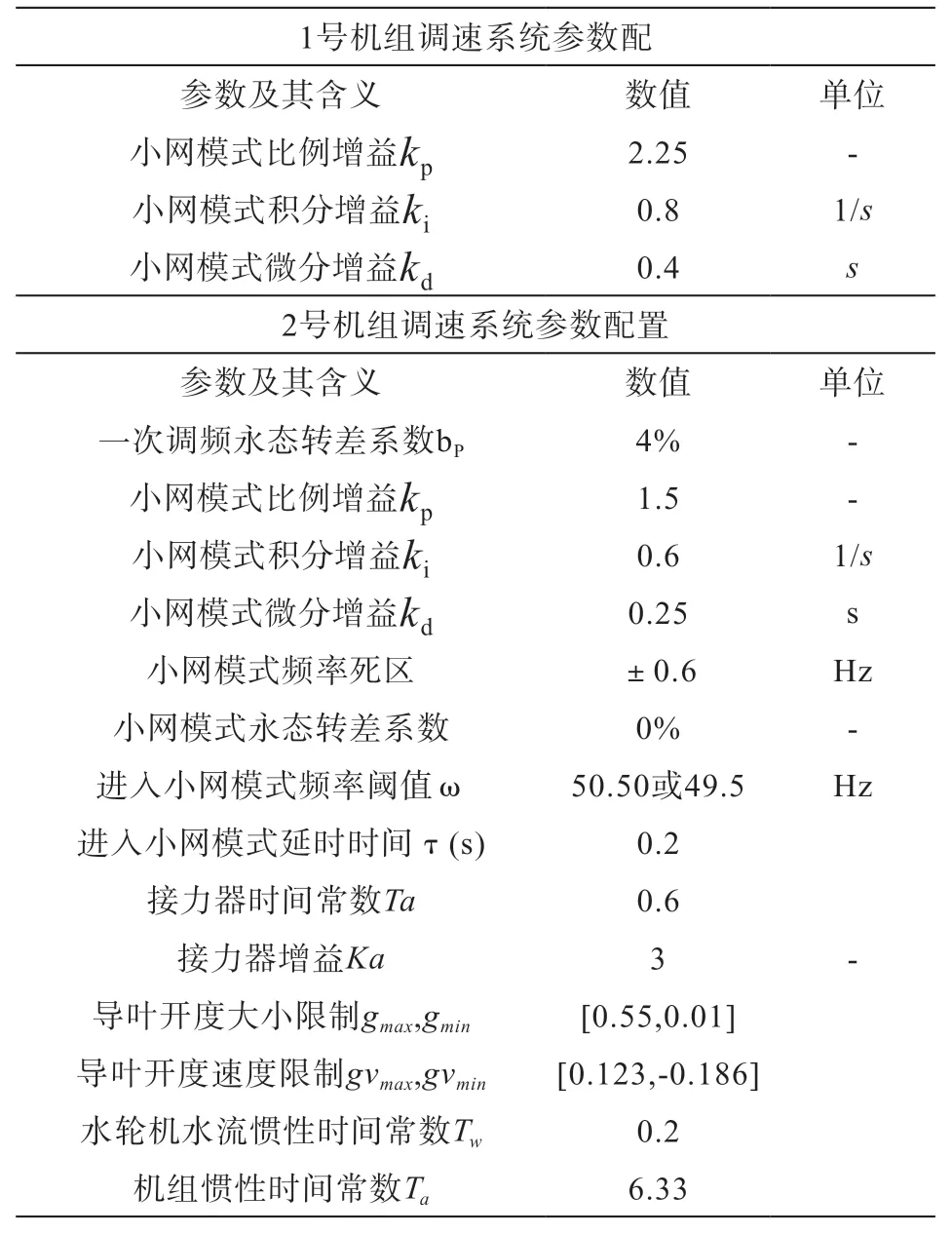
表1 調速系統參數初始化配置

3.4 安南電站孤網運行穩態驗證

3.4.1 安南電站1，2號機組供白水臺及東壩線穩態運行過程

斷開011 后1，2 號機組供白水臺及東壩線運行過程，最高頻率50.55 Hz，最小頻率49.35 Hz，滿足GB/T 9652.1-2019《水輪機調速系統技術條件》中孤網運行頻率不超過±3%的要求。

圖8 1、2號機組小網模式穩態運行過程（單位 / s）

3.4.2 安南電站1機組供白水臺線穩態運行過程

1 號機組供白水臺線穩態運行過程，最高頻率50.83 Hz，最小頻率49.29 Hz（線路負荷有波動情況下），滿足GB/T 9652.1-2019《水輪機調速系統技術條件》中孤網運行頻率不超過±3%的要求。

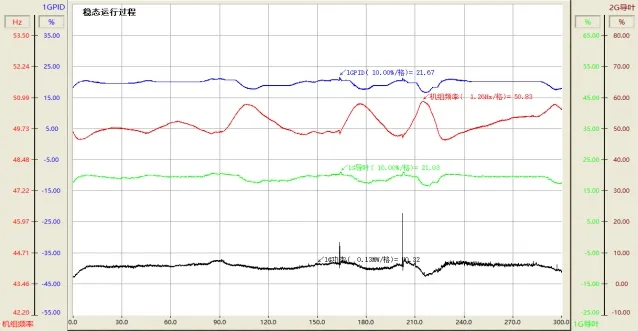
圖9 1號機組小網模式穩態調節過程

3.4.3 安南電站1機組與儲能系統共同供白水臺線、鄉政府線、江邊哈巴線穩態運行過程

1 號機組與儲能、光伏系統供白水臺線、鄉政府線和江邊哈巴線穩態運行，頻率波動范圍減小（線路負荷有波動情況下），最高頻率49.88 Hz，最小頻率49.64 Hz（線路負荷有波動情況下）。

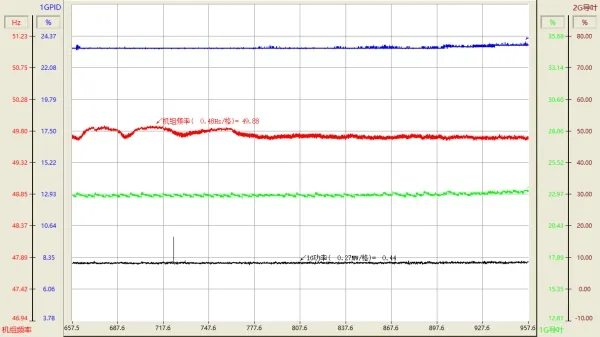
圖10 水、光、儲小網模式穩態調節過程

安南電站1、2 號機組調速系統導葉開度、PID 輸出、功率信號、頻率信號、小網動作信號量值，實測信號數據正確且真實有效。

試驗分別進行了安南電站1、2 號機組帶白水臺及東壩線運行、1 號機組帶白水臺線運行、1 號機組及儲能系統帶白水臺線、鄉政府線及江邊哈巴線運行，試驗過程中的指標均滿足相關標準要求，驗證了安南電站1、2 號機組調速系統小網模式相關參數配置的合理性，同時也驗證了安南電站具備微電網組網能力。

4 結束語

1）通過DE 算法以及小水電機組調速系統仿真評價模型可以有效優化實際機組系統PID參數，使得現場參數辨測次數減少，提升了機組參數優化的效率；

2）實際應用中可把基于ED 算法的小水電機組調速系統PID 參數仿真優化方法和現場實測方法相結合，減少實測次數和范圍；

3）繁瑣的改進DE 算法并不適合現場工程應用，對參數優化結果支撐性不足，故實際工程應用中不推薦改進的DE 算法，應尋求更合適的智能優化算法，提升優化效率和精度。