V2500 發動機短艙維修間隔確定方法

■ 陳鍵 孫良臣/中國南方航空股份有限公司工程技術分公司沈陽基地

0 引言

維修是保證飛機持續適航的重要手段，在整個運營期間必須重點關注。國外主制造商的航空基礎雄厚，積累了大量歷史數據，可以用來支持飛機維修大綱的制定[1]。對于現行飛機的維修大綱，發動機短艙件的維修要求僅包含在區域檢查項目中。為了更好地維護V2500 發動機短艙部件，必須制定具體的維修要求，其中維修間隔的確定尤為關鍵，維修間隔的設置直接影響到飛機的可靠性和維修成本[2]。

1 基于成本和可用性的分析方法

1.1 維修間隔制定策略及可用性和成本分析

假定在每次檢測中，正常結構仍然原樣使用，僅當發生損傷時才需恢復到新的狀態。如果在檢查時發現系統工作，假設系統保持不變；當檢測到故障時，在維修/更換時間后更新。推導出由于檢查和維修/更換而導致隨機停機的可用性模型，如圖1所示，然后將恒定檢查時間和維修/更換時間作為特例進行研究。

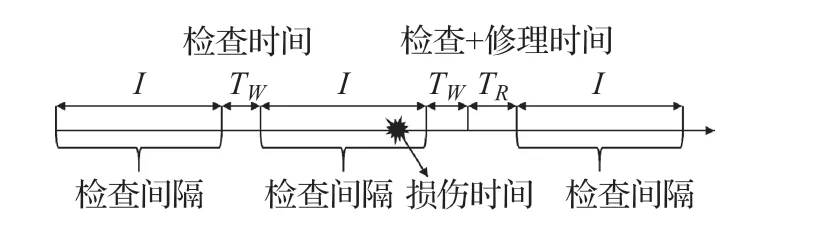
圖1 檢查周期示意圖

首先研究預期的周期時間，如表1 所示。對于特定的X0、Y0、X1，周期時長為：

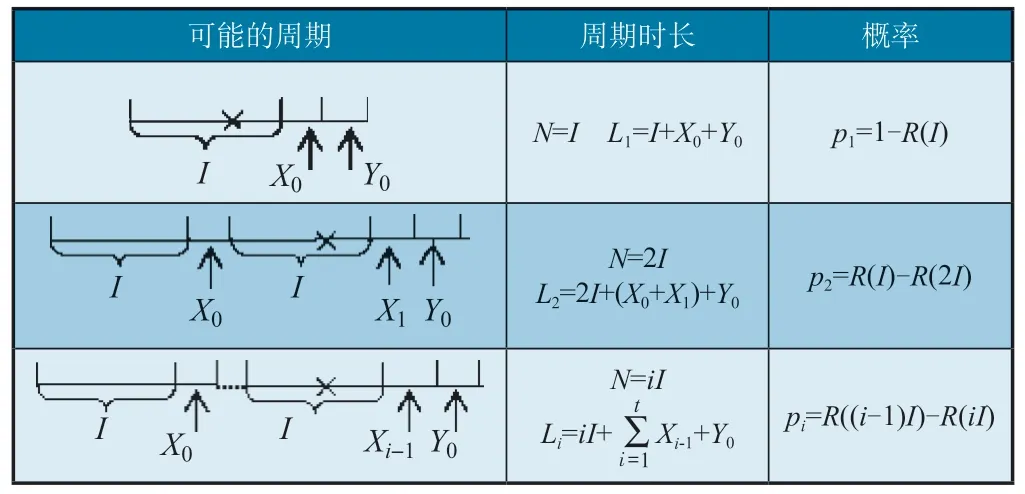
表1 周期時間

預期的周期時間為：

預期不能工作的時間為：

一個周期內的預期總成本包括以下成本：

1.2 損傷數據的整理

對于航司V2500 發動機短艙的原始維修紀錄，分別按進氣道、風扇罩、C 涵道、平移門和尾噴5個主要部件進行記錄，刪除重復或錯誤的記錄，留下每個部件不同時間下的唯一記錄。對于同一主要部件的多次維修記錄，則使用后面的時間減去前一個時間，獲得其維修間隔。對于短艙系統采取以上的相同操作，若同一次維修了多個部件，僅作一次記錄數據。

1.3 確定最優檢查間隔

威布爾分布作為一個典型壽命分布模型，在飛機及部件可靠性評估方面有著廣泛應用[3-5]。基于經過數據整理的維修記錄數據，獲得進氣道、風扇罩、C 涵道、平移門和尾噴等5 個主要部件的維修信息和壽命，然后采用MATLAB程 序“weibull_parameters_get.m”，分別獲得各自部件雙參數威布爾分布的參數beta 和eta。維修平均工時（TR）、平均檢查工時（TW）、檢修停機時間（TF）、維修平均費用（CR）、單位停機成本（CL）及單位檢查費用（CW）均來自航司內部數據，獲得的最終輸入數據見表2。將最終數據代入公式（3）和公式（6），便可獲得基于可用性和成本的最優檢查間隔及相應的優化曲線，如圖2、圖3所示。通過確定曲線的極值，便可得到兩種分析方法的最優檢查間隔。

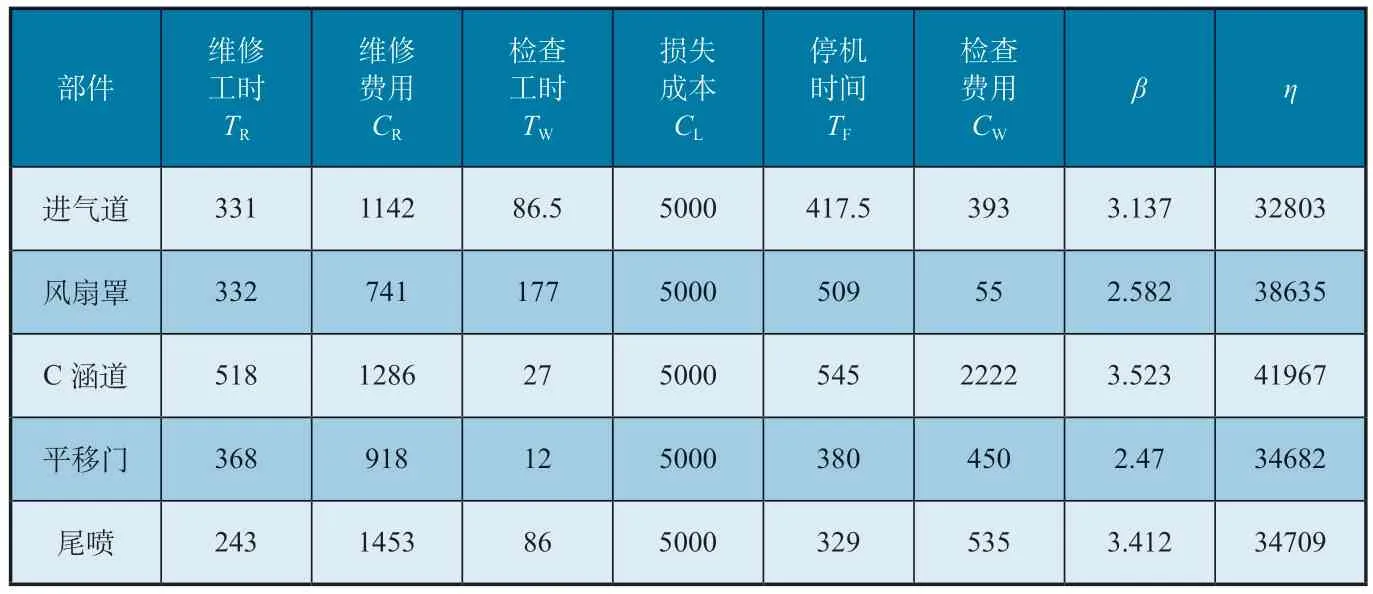
表2 參數數據

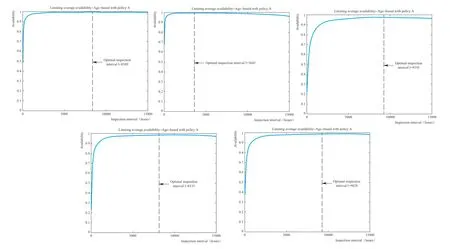
圖2 各部件可用性最大的最優檢查間隔

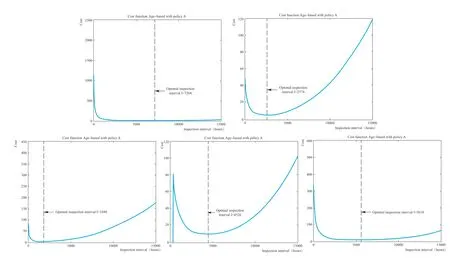
圖3 各部件成本最低的最優檢查間隔

2 基于大數據和AI 模型的分析方法

監督學習就是分類，通過已有的訓練樣本去訓練得到一個最優模型，然后利用這個最優模型將所有輸入映射為相應的輸出，對輸出進行判斷實現分類，這就對未知數據進行了分類。監督學習中的K-近鄰方法（K-Nearest Neighbor，KNN）[6，7]和 支 持 向 量 機（SVM）[8]均可用于分析V2500 發動機短艙的維修記錄數據。在對發動機短艙的維修記錄數據進行大數據分析建模時考慮基于特征進化的損傷模型，即將包括發動機位置（左/右）、損傷部位（左/右）、損傷是否超手冊（是/否）和損傷威脅維修方案（修理/更換）等損傷特征的持續記錄作為大數據分析的數據向量，以考慮這些客觀特征對飛機（機隊）維修數據模型的影響。

對于V2500 發動機短艙的維修記錄數據，采用matlab 的coxphfit 函數擬合，可 得η=1485.2，β=2.6814，γ0=0.0422，γ1=0.0194，γ2=0.0327，γ3=0.0159。（Zti=0，1，2，3）分別代表相應的特征參數：發動機（Engine，0-左，1-右）；部位（Position，0-左側，1-右側）；是否超 手 冊（Manual，0- 否，1- 是）；損傷威脅維修方案（Damage，0-修理，1-更換）；修理的部件（1-進氣道，2-風扇罩，3-C 涵道，4-平移門，5-尾噴，LR 為保留參數）。采用python 的scikit-learn 庫進行機器學習，分為數據加載、數據預處理、數據劃分、數據訓練和效果評估等步驟。

2.1 K-近鄰方法（K-Nearest Neighbor，KNN）

通過計算每個訓練樣例到待分類樣品的距離，取與待分類樣品距離最近的K個訓練樣例，K個樣品中哪個類別的訓練樣例占多數，則待分類樣品就屬于哪個類別。如果一個樣本在特征空間中的K個最相鄰的樣本中的大多數屬于某一個類別，則該樣本也屬于這個類別，并具有這個類別上樣本的特性。該方法在確定分類決策上只依據最鄰近的一個或者幾個樣本的類別來決定待分類樣本所屬的類別。KNN 方法在類別決策時，只與極少量的相鄰樣本有關。由于KNN 方法主要靠周圍有限的鄰近的樣本來判斷，而不是靠判別類域的方法來確定所屬類別，因此對于類域的交叉或重疊較多的待分類樣本集來說，該方法較其他方法更為適合。

上述案例中KNN 模型設置neighbor 數目為5，test_size=0.2。通過訓練模型，可預測各飛機發動機短艙下次出現故障的部件和時間間隔，如表3所示。

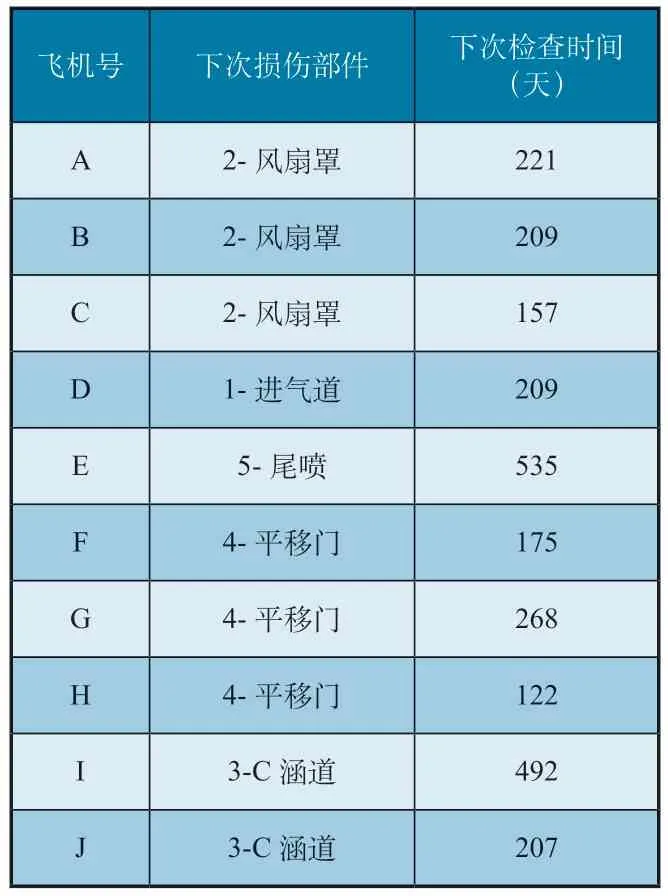
表3 KNN方法預測結果

2.2 支持向量機（SVM）

支持向量機（SVM）就是找到一個平面，讓兩個分類集合的支持向量或者所有的數據（LSSVM）離分類平面最遠；SVR 回歸，就是找到一個回歸平面，讓一個集合的所有數據到該平面的距離最近。SVR 是支持向量回歸（support vector regression）的英文縮寫，是支持向量機（SVM）的重要應用分支。

上述案例中SVR 模型設置test_size=0.2。通過訓練模型，預測各飛機發動機短艙下次出現故障的部件和時間間隔，如表4 所示。

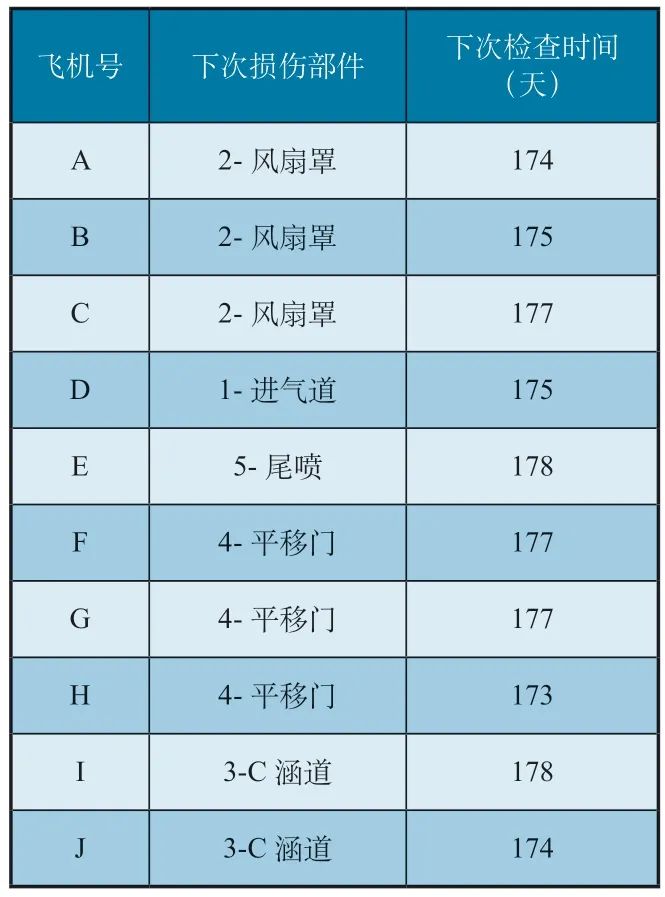
表4 SVR方法預測結果

3 結論

采用基于成本和可用性的分析方法時，只需要獲得發動機短艙部件的維修間隔記錄，就可以通過威布爾分布擬合獲得其壽命分布，在已知維修成本和時間基本信息的情況下獲得穩定的最優維修間隔。基于大數據和AI 模型的分析方法不預先假設發動機短艙部件的維修間隔分布，而是基于已有的記錄數據（包括歷史維修間隔和其他損傷信息）預測短艙部件的下一次故障時間（即維修間隔）。

基于成本和可用性的分析方法的優點是：需要的記錄數據較少；數據確定的情況下，結果穩定。缺點是：只能獲得固定的最優檢測間隔；只能利用維修記錄中的時間信息，無法利用其他與損傷相關的參數/變量信息。

基于大數據和AI 模型的分析方法的優點是可以預測每個部件下次的失效日期，可以對每個部件設定不同的檢測間隔；可以綜合利用維修記錄中包括時間在內的所有與損傷相關的參數/變量信息。缺點是需要大量的記錄數據以訓練模型，在數據較少時獲得的模型的可靠性較低，且每次訓練可能得到不同的模型，結果不穩定，不同方法的結果存在差異。

綜上，在確定V2500 發動機短艙維修間隔時，應盡可能記錄與發動機短艙部件的維修、服役歷史、服役環境相關的所有信息并對其進行電子化整理，建立相關的數據庫，通過綜合使用上述兩種方法，制定更加準確的維修間隔。