基于有理插值方法模擬SMAs循環加載下的變形行為

王曉明, 肖 衡

(1.寧波職業技術學院 應用力學研究所,浙江 寧波 315000;2.暨南大學 力學和建筑工程學院,廣州 510632)

0 引 言

因具有獨特的形狀記憶效應(shape memory effect,SME)、偽彈性(pseudo-elasticity,PE)、拉伸-壓縮不對稱以及生物兼容性等特征,形狀記憶合金(SMAs)被廣泛應用于航天航空[1]、機器人制造[2]、生物醫療[3]等領域．SMAs構件在實際使用過程中往往需要受到反復加載-卸載的作用,應力-應變關系從一開始的塑性變形逐漸轉變為偽彈性變形．通過構建SMAs本構模型,模擬其在循環荷載作用下的變形行為,具有十分重大的工程價值．

SMAs自從被發現以來就受到了巨大的關注,尤其是近幾十年來,其本構建模的理論不斷被提出,綜述文獻也有很多[4-9],我們大致可以將這些理論分為三大類,即微觀模型、介觀模型和宏觀模型．微觀模型在晶格和晶粒尺度上描述晶核生長、馬氏體孿晶生長等特征．其中,Falk[10-11]基于Ginzburg-Landau理論提出了多項式[12]勢能模型．Daw等[13]運用分子動力學理論構建了SMAs微結構模型．介觀模型首先需要建立微觀尺度下的本構關系,然后通過平均方法等尺度轉換方法建立宏觀本構．其中,Wang等[14]基于馬氏體相變[15-16]和晶體塑性理論構建了三維模型,研究了馬氏體塑性變形產生的不可恢復變形．Taylor等[17]引入微平面理論,認為SMAs的多軸宏觀力學行為是不同取向微平面單軸相應的疊加．該方法隨后被用于模擬超彈性、偽彈性行為[18]．宏觀模型不再考慮材料內部結構理論,而是從宏觀特征出發推導本構方程．其中,Tanaka[19]利用非線性彈性方法構建了一個一維本構模型,其馬氏體體積分數演化方程通過一種分段方程給出;Brinson[20]進一步發展了他的理論,將馬氏體體積分數分解為自適應部分和非自適應部分;Lagoudas等[21]利用彈塑性理論構建了SMAs宏觀本構,馬氏體相變、退孿晶等熱力學過程受到加載函數和流動法則的影響; Zaki等[22]通過熱力學勢函數構建了三維模型,引入了三個新的內變量來解釋循環作用下的SMAs“訓練”(training)和雙程形狀記憶效應(TWSME)．

近幾十年以來,關于SMAs循環荷載作用下的實驗研究有很多[22-24]．這些實驗結果表明,循環荷載下,馬氏體在正相變、逆相變作用下,塑性不可恢復變形逐漸累計,相變轉化初始應力和耗散能逐漸減少,相變硬化逐漸增大．每一個循環下的應力-應變關系從初始的塑性變形,逐漸轉化為偽彈性變形．當循環達到一定量以后,應力-應變滯回圈趨于一種穩定狀態,且累計的塑性變形等量變成飽和狀態．通過透射電子顯微鏡(TEM)技術研究循環作用下SMAs的微觀結構,科研工作者們發現,不可恢復變形累積的主要微觀機制是奧氏體相的滑移和不完全擬相變形成的殘余馬氏體相[25]．

在實驗的基礎上,眾多學者提出了SMAs本構模型對循環加載下的變形行為進行模擬,可參考綜述文獻[26]．這些模型分別從宏觀唯象和微結構機制兩個方向進行建模．早期的唯象模型[4,20,27]只考慮了循環作用下的馬氏體相變,無法模擬塑性應變累積、殘余馬氏體相退化等情況．Bo和Lagoudas[28-30]在原模型的基礎上,引入了新的內變量來表征馬氏體相變和塑性變形相互作用產生的影響,提出了一個改進的模型;Auricchio等[31-32]考慮了相變閥值和殘余變形量,模擬了SMAs的“訓練”和雙程形狀記憶效應;Zaki和Moumni[33]引入了馬氏體體積分數和馬氏體定向應變張量兩個狀態變量來解釋偽彈性和單程形狀記憶效應,后續又提出了包括累積馬氏體體積分數在內的三個新的內變量來表征循環加載下的變形特征．另外,微結構理論從SMAs微觀機制推導模擬循環加載變形．Patoor等[34-35]基于物理應變機制和局部熱力學勢的定義構建了動力學表述的微結構模型,馬氏體體積分數作為內變量用來描述內結構狀態的演化;Huang等[36]發展了一種單晶模型,利用一定數量隨機方向的單晶顆粒通過平均方法構建了多晶SMAs本構模型;Lagoudas和Entchev[37]提出了一個致密SMAs三維本構模型,用來解釋循環荷載下的相變、塑性應變以及滯回圈形狀和大小的演化規律;Kang等[38]通過“應變控制”的循環加載實驗發現了SMAs的荊輪變形行為．隨后,Yu等[39-40]基于晶體塑性理論解釋了循環加載下的非彈性變形機制,如馬氏體相變、相變誘導塑性、馬氏體再定向等．

以上模型在模擬循環加載下SMAs塑性變形和偽彈性變形的時候,通常需要分別引入額外的內變量,這些量的演化方程需要引入多個隱式參數,這就給計算帶來了非常大的挑戰．為了解決以上問題,一種顯式方法被提出,用于構造SMAs和類橡膠材類的本構模型[40-49]．本文在之前研究[50]的基礎上,基于有理插值的方法,提出了一種新的有限彈塑性J2流模型,用來同時精確模擬SMAs在循環荷載下的塑性變形和偽彈性變形．

全文主要安排如下:首先,基于有理插值的方法給出了循環加載下的形函數形式,對任意形狀的應力-應變滯回圈都能精確模擬;其次,構建了新的有限彈塑性J2流模型;再次,從單軸情況出發,經過多軸擴展、局部因子引入等步驟,得到了多軸有效的硬化模量顯式表達;最后,選取經典的實驗數據和新模型得到的結果進行對比,證明了該方法的有效性,并給出了結論．

1 基于有理插值的形函數

在控制最大應力不變的前提下,對SMAs試件進行反復加載-卸載,其應力-應變關系如圖1所示．先分析循環荷載下應力-應變關系的特征,再分別分析每一次循環過程中,加載和卸載情況下的形函數,最后利用有理插值具體給出屈服階段的形函數表達,對任意形狀的應力-應變滯回圈都可以精確模擬．使用的應力為Kirchhoff應力,應變為對數應變,也稱為Hencky應變,并用有效塑性功代替傳統的塑性功．

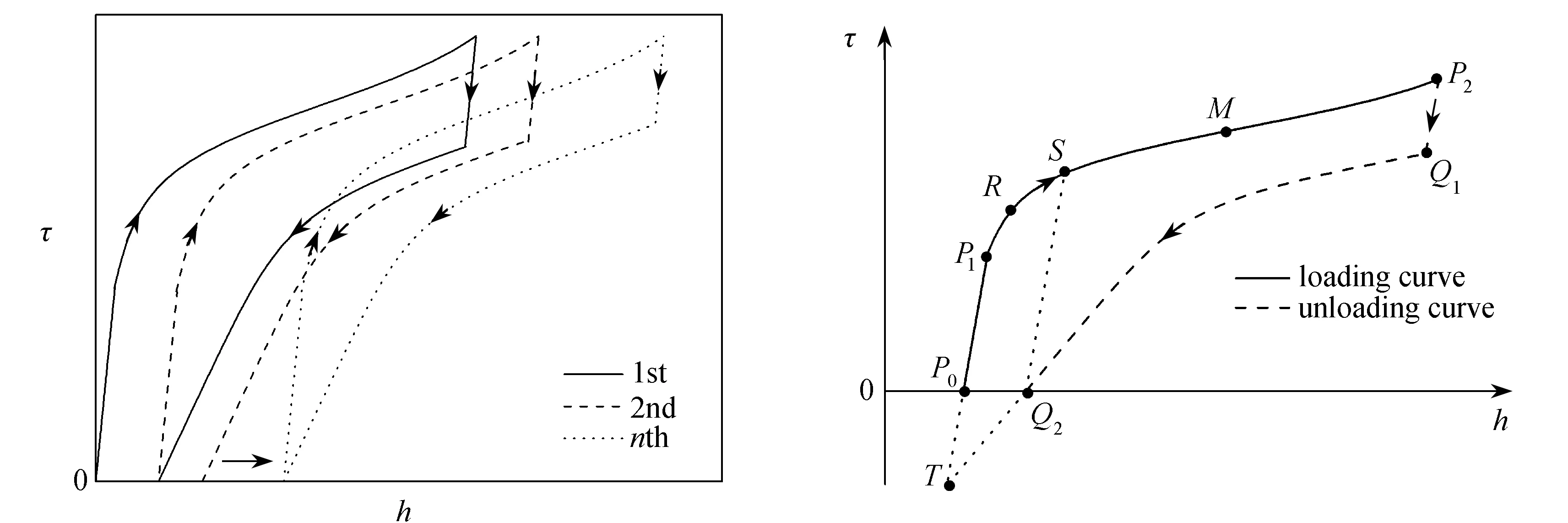
圖1 循環荷載下的應力-應變示意圖 圖2 第i次循環下的應力-應變示意圖Fig.1 Schematic of stress-strain curves under cyclic loading Fig.2 Schematic of stress-strain curve in the ith cycle

1.1 循環荷載下的變形特征

圖1表示從第1次到第n次循環下的應力-應變關系．對圖1分析可知,循環荷載下SMAs應力-應變關系特征如下:

1) 每一次加載-卸載循環都會形成一個不完全封閉的滯回圈．從第一個循環到最后一個循環總共產生n個應力-應變滯回圈,其中第n個循環已經完全封閉且穩定．

2) 每一個應力-應變滯回圈由加載和卸載兩部分組成．其中,加載部分包括彈性階段和上屈服階段,卸載部分包括彈性階段和下屈服階段．

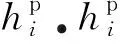
4) 當循環次數接近甚至到達n時,應力-應變滯回圈穩定,且不可恢復變形量不再繼續增加,此時

1.2 加載和卸載階段形函數

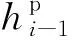
(1)

點P1表示加載部分從彈性階段變成屈服階段的過渡點,該點的應力即為屈服強度,用r0表示,應變用h0i表示,而有效塑性功與點P0一樣,為?i-1．P1P2段表示加載部分的屈服階段,也就是上屈服階段,該段的應力-應變形函數用

(2)

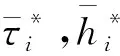
(3)

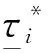
(4)

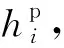
形函數中關鍵點應力、應變和有效塑性功如表1所示．根據式(1)—(4)可得

(5)

表1 形函數中關鍵點應力、應變和有效塑性功Table 1 Stresses,strains and effective plastic works of key points in the shape function

1.3 上下屈服形函數關系

筆者之前的研究中[47]用了一種線性關系來表示上下屈服應力之間的一一對應關系,即為

(6)

任意一個下屈服形函數中的點必然有一個點和上屈服形函數對應,比如圖2中的點T對應點P1,點Q2對應點S,點Q1對應點P2．其中bi是可調參數,若bi=1,則表示上下屈服形函數平行,這種情況可以處理簡單的偽彈性特性[41],而μ0i則表示圖2中點S所對應的應力大小．

利用方程(2)、(4)和(6),得到上下屈服形函數之間的關系為

(7)

即只要給定上屈服形函數的具體形式,就可以通過方程(7)推導得到下屈服形函數．

1.4 基于雙曲正切函數的有理插值方法

基于雙曲正切函數的形函數形式,可以精確匹配上屈服流的應力-應變數據,其具體形式為

(8)

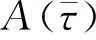
(9)

將方程(8)代入到方程(7)中,可以得到下屈服段的形函數,其中涉及到的兩個關鍵參數為bi和μ0i．接下來給出這兩個參數的確定方法．

(10)

從以上方程可以得到

(11)

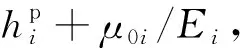
(12)

利用方程(9)可得

(13)

2 有限彈塑性J2流模型

有限彈塑性本構模型的類型有很多,本文采用基于對數客觀率的表述形式[51]．首先通過伸縮率分解的形式給出基本方程,然后耦合強化效應,改進背應力演化方程．

2.1 基于伸縮率分解的基本方程

基于Euler表述的有限彈塑性模型滿足自洽條件[51],其基本方程是基于伸縮率的分解的形式,即

D=De+Dp,

(14)

其中D為速度梯度的對稱部分,也就是伸縮率,De表示彈性部分,Dp表示塑性部分．

彈性部分可以通過Hooke定律給出

(15)

(16)

塑性部分通過流動法則[53]給出:

(17)

式中,ξ表示塑性指數,加載情況下,其值為1,卸載情況下為0,u表示塑性模量,f表示von Mises屈服函數,其表達式為

(18)

2.2 強化效應耦合

有效塑性功隨著塑性流的發展單調遞增,且和熱力學內耗散直接相關．因此本文用有效塑性功代替傳統的塑性功,其表達為

(19)

為了使本構模型耦合屈服面半徑大小和屈服中心移動,屈服強度r不僅依賴于有效塑性功?,還和背應力相關,即

r=r(?,ζ),

(20)

其中ζ的大小完全依賴背應力張量,其表達為

(21)

背應力的演化方程遵循新的各向異性強化法則:

(22)

(23)

方程(20)和(23)確保了模型耦合兩種強化效應,3個硬化含函數c,ω和r的具體形式將在第3節中給出．接下來需要確定塑性模量u的表示,可以由以下公式推導[47]:

(24)

其中4階張量H為

(25)

(26)

其中

3 硬 化 函 數

為了從第2節構建的有限彈塑性J2流模型中推導得到符合要求的結果,需要給出硬化函數c,ω和r的具體形式．首先推導得到單個循環下的硬化函數形式,再給出有效塑性功的演化規律,最后引入依賴塑性功的局部因子,構造統一光滑的硬化函數顯式表達．

3.1 單個循環下的硬化函數

單循環下的硬化函數推導需要從塑性坡度出發,利用方程特點分別給出ci,ωi和ri,再通過推導相鄰循環下屈服函數的表達,證明其符合內循環一致性條件．

3.1.1 塑性坡度

由方程(17)、(18)、(19),再結合塑性模量的表達(方程(24)),推導得到單軸情況下有

(27)

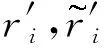
(28)

方程(27)和(28)給定的形式只是單軸有效,為了擴展成多軸有效,需要將塑性坡度改進為

[ri+Λi]=0.5(ri+Λi+|ri+Λi|)．

(29)

將改進后的塑性坡度代入到方程(27),得到單個循環下多軸有效的形式為

(30)

3.1.2ci,ωi和ri

將方程(30)轉化為以下形式:

(31)

以上方程要得到有效的ωi,必須滿足分子和分母同時為0,即

(32)

從方程(32)可以推導得到

(33)

將方程(33)代入到方程(31),得到

(34)

接下來考慮屈服極限ri的表達．在Xiao[41,48]和Wang等[42]研究的基礎上,進一步考慮有效塑性功的局部性特點,得到屈服極限表達為

(35)

式中,r0表示初始屈服強度,兩個非負參數β2和β3分別表示ζ=0和?=?i(或?i+1)的局部特征,

μi=(r0-μ0i)/bi,i=1,2,3,…,n．

(36)

3.2 有效塑性功演化規律

從第1次循環開始,到第n次循環結束,每一次循環都伴隨著有效塑性功的累計,本小節給出其在循環荷載下的演化規律．用?i(i=1,2,3,…,n)表示每一次循環結束后的有效塑性功大小．

根據方程(35)和(36),在忽略局部特征的前提下,得到單循環下塑性強度為

(37)

(38)

根據方程(14)、(15)和(17),在單軸情況下的塑性應變為

(39)

根據方程(6),單軸下的有效塑性功為

(40)

將方程(39)代入到方程(40),再結合屈服條件,得到

(41)

對方程(41)進行積分,并結合方程(8)形函數的形式,可以得到單個循環下,圖2中累計的有效塑性功大小,在μ0i∈[r0,r+rmi)的情況下為

?i=?i-1+2Z1-Z2,?0=0,i=2,3,…,n,

(42)

其中

(43)

在μ0i∈[r+rmi,∞)的情況下為

?i=?i-1+2Z1-(Z0+Z3),?0=0,i=2,3,…,n,

(44)

其中

(45)

上屈服階段P1P2之間必然有一個點的應力為r0+rmi,假設該點用M表示,如圖2所示．Z1表示P1-P2階段累計的有效塑性功,也等于Q1-T階段積累的有效塑性功;在μ0i∈[r0,r+rmi)的情況下,點S在點M前面,Z2表示P1-S階段累計的有效塑性功,也等于Q2-T階段積累的有效塑性功; 在μ0i∈[r+rmi,∞)情況下,點S在點M后面,Z3表示M-S階段累計的有效塑性功,Z0表示P1-M階段積累的有效塑性功．因此,Z0+Z3可以表示P1-S階段的有效塑性功,也等于Q2到T的有效塑性功,其效果和μ0i∈[r0,r+rmi)情況下的Z2一樣．

3.3 統一光滑硬化函數

式(31)、(33)和(35)分別給出了每一個循環下的ci,ωi和ri,i=1,2,3,…,n．本小節在前面的基礎上構造一個光滑統一的硬化函數表達,使其對n個循環過程均適用．

這里通過n個局部因子,將得到的所有單循環硬化函數進行簡單的線性插值,得到

(46)

其中,局部因子具體形式為

(47)

φi具備如下特點:當有效塑性功?∈[?i,?i+1)時,其值為1,其他情況下均為0．由此可得,在第i次循環下硬化函數自動退化為ci,ωi和ri．

4 模型結果與實驗結果對比

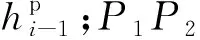
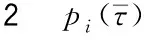
表2 中固定參數值Table 2 Values of fixed parameters in

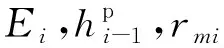
(48)

其中?=0,表示第1次循環的情況,此時i=1．在本例中μ0i∈[r0,r+rmi),每一個循環下的有效塑性功結合方程(42)和(43)給出,代入到方程(48)就可以得到每一循環下的參數值．再利用方程(13)就能確定μ0i的大小,最終得到的模型結果和實驗結果如圖3所示．

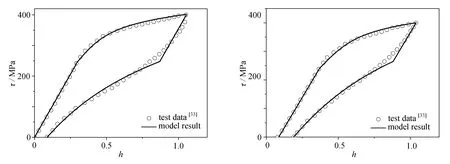
(a) 第1個循環 (b) 第2個循環(a) The 1st cycle (b) The 2nd cycle

(c) 第3個循環 (d) 第4個循環(c) The 3rd cycle (d) The 4th cycle

(e) 第8個循環 (f) 第12個循環(e) The 8th cycle (f) The 12th cycle

(g) 第20個循環(g) The 20th cycle圖3 第1、2、3、4、8、12和20次循環的模型結果和實驗結果[33]對比Fig.3 Comparation between model results and experimental data[33] for the 1st,2nd,3rd,4th,8th,12th and 20th cycles

模型預測結果如圖4所示．其中由外到內的實線分別表示第4、5、6、7和8次的模型結果．其中第4和第8次的結果和實驗數據可以精確匹配(從圖3(d)、3(e)數據對比可得),而第5、6和7次的實驗數據,新的模型可以合理地預測．第5次循環開始時的應變和第4次結束時一致,而第7次循環結束時的應變和第8次開始時一致．

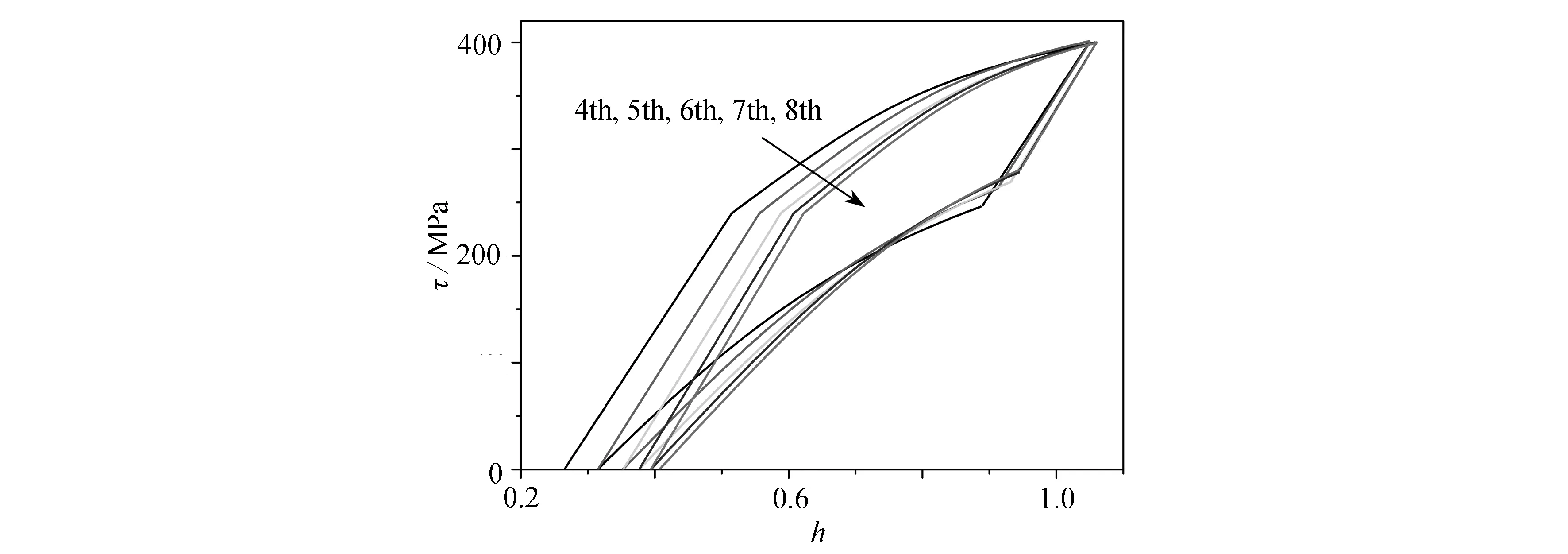
圖4 第4至第8個循環的模型預測Fig.4 Model predictions from the 4th to the 8th cycles

5 結 論

本文通過提出新的有限彈塑性J2流方程,模擬了SMAs在循環荷載下從塑性變形逐漸轉化為偽彈性變形的過程．所得主要結論如下:

1) 新的本構方程耦合了屈服中心的移動和屈服面的增大,使得模型可以模擬SMAs復雜的變形行為．傳統的金屬材料在加載后卸載,卸載階段的應力-應變關系一般遵循Hooke定律．卸載應力到0以后進行反向加載才會開始出現下屈服階段,也就是Bauschinger效應．本文通過改進背應力的演化方程,提出硬化模量c,ω和r的新形式,使得SMAs在卸載應力為0之前就開始屈服,進而產生滯回圈．

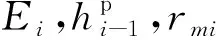
3) 從第2節的基本方程出發,結合形函數具體形式,得到了有效塑性功的演化規律,如方程(43)和(45)所示．利用這些方程可以得到每一個循環下?的累積大小,進而通過方程(49)給出的參數方程,確定該循環下的參數值,從而得到循環的應力-應變滯回圈．

4) 由局部因子構造而成的統一光滑硬化模量c,ω和r如方程(47)所示,這些量在單循環下會自動退化成符合要求的形式,將這些硬化模量代入到本構方程以后,能夠得到符合要求的結果．通過圖3的模型結果和實驗結果比較,證明了本文方法得到的結果可以精確匹配實驗結果．此外,對于沒有采集實驗數據的循環,利用方程(49)推導的參數也可以進行合理地預測,如圖4所示．

致謝本文作者衷心感謝寧波職業技術學院研究機構專項課題(NZ21JG008)對本文的資助．