低Weissenberg數黏彈性流體中單氣泡上浮運動特性研究

張仕環, 龐明軍, 鄭智穎

(1.常州大學 機械與軌道交通學院,江蘇 常州 213164;2.哈爾濱工業大學 能源科學與工程學院,哈爾濱 150001)

0 引 言

氣液兩相流廣泛存在于自然界和工業過程中,如血液中的氣泡運動[1],石油輸送過程和鼓泡塔內的氣泡上浮運動等[2]．氣泡的存在會對液相的運動、傳熱傳質和表觀黏度等特性產生顯著的影響[3]．因此,研究液相中氣泡的運動特性對工農業生產和日常生活具有重要意義．工業過程涉及的液相多為非Newton流體,而黏彈性流體又是一種典型的非Newton流體,因此研究黏彈性流體中的氣泡運動特性意義重大．

為了理解氣泡在非Newton流體中的水動力學特性,前人已經開展了大量的研究[4-19],但關于氣泡在黏彈性流體中水動力學特性的研究相對較少．特別是國內學者僅開展了為數不多的實驗研究[20-22],理論和數值研究鮮見報道．國外學者Astarita和Apuzzo[23]開創性的實驗發現,在黏彈性流體中,當氣泡體積大到一定程度時,其上浮速度會突然增大(所謂的“速度不連續性階躍”),氣泡形狀呈現為倒置的淚滴狀．Hassager[24]實驗發現氣泡在黏彈性流體內上浮時,其中心尾跡出現了向下流動(即“負尾跡”)的現象,與鋼球在黏彈性流體中下沉時的流線形狀相似[25]．此后,一些學者實驗再現了黏彈性流體中氣泡上浮的典型特征[26-30]．

在數值研究方面,Wagner等[31]使用格子Boltzmann方法研究了黏彈性流體中二維氣泡的上浮運動,再現了實驗中發現的帶尖尾部．Pillapakkam等[32]使用水平集方法(level set method),研究了三維氣泡在黏彈性Oldroyd-B液體中的上浮運動,再現了上浮速度不連續階躍的現象．Fraggedakis等[33]基于Phan-Thien Tanner(PTT)黏彈性模型,使用任意Lagrange-Euler法很好地預測了在達到臨界體積時氣泡速度突然增加的現象．然而,隨著研究者們對強彈性流體的數值計算遇到了數值問題,即高Weissenberg數問題(the high Weissenberg number problem,HWNP),為了解決該問題眾多學者進行了深入的研究[34-36]．Yuan等[37]在對構象張量進行對數化處理后,使用流體體積(VOF)法研究了高Weissenberg數下氣泡在黏彈性流體中的上浮運動特性．Ohta等[38]基于剪切稀化Carreau模型和FENE-CR黏彈性模型考慮流體的剪切稀化和黏彈性特征,使用水平集和流體體積耦合方法(CLVOF)研究了具有剪切稀化特征黏彈性流體中氣泡的上浮運動．

綜上所述,盡管國內外學者針對黏彈性流體中氣泡的上浮運動特性開展了一定的研究,并得到了一些有價值的結論,但相關現象的機理解釋仍難以定論．再加上黏彈性流體自身的復雜特性,研究難度相對較大,國內關于這方面的理論和數值研究鮮見報道．特別是當Weissenberg數太大時,開展黏彈性流體的數值計算會遇到“高Weissenberg數問題”,即構象張量分量呈指數增長會導致計算的不穩定性．在實際工業應用中,也經常會遇到彈性較弱(Weissenberg數較小)的黏性流體,比如低分子量(短鏈)或低濃度的聚合物溶液．為了理解氣泡在黏彈性流體中的上浮運動特性,使用數值模擬方法嘗試研究了低Weissenberg數下松弛時間、黏性力、表面張力和黏度比對氣泡上浮運動特性的影響,詳細分析了氣泡形狀、上浮速度、尾渦和彈性應力的分布特征,為后續深入研究奠定基礎．

1 物理問題和計算模型

1.1 幾何模型

目前公開發表的數值研究氣泡在Oldroyd-B黏彈性流體運動的文獻中[32,37],氣泡形狀基本是左右對稱的(除了非穩態工況外),且影響氣泡形狀的因素基本位于氣泡輪廓平面內．本文通過研究低Weissenberg數下,黏性力、松弛時間、表面張力和黏度比對氣泡形狀的影響來反應氣泡上浮時的運動特性,所以將計算域簡化為二維平面時,氣泡的形狀基本不會受到太大影響．盡管對于二維平面假設,圓形氣泡不是真實的球形氣泡而是一個圓柱體,導致氣泡尾流和上升阻力存在一定的偏差,但總體上二維平面計算能定性地反映一定的流動特征[39-41]．而且目前的計算是在低Weissenberg數下進行的,氣泡上浮速度相對較小,在一定程度上能將流動失真降低到可接受范圍內．另外,目前二維的計算結果,比如氣泡形狀、速度以及流場信息與文獻基本吻合[37]．所以目前二維計算的假設是合理的,既能極大地減小計算成本,又能較全面地研究不同參數對氣泡在黏彈性流體中上浮運動的影響．

計算區域設置為一矩形區域,如圖1所示．矩形區域內充滿黏彈性流體,初始半徑R=2.5 mm的圓形氣泡受浮力作用從底部自由上浮．為了消除壁面的影響,以及能使氣泡運動取得充分發展,矩形區域的高和寬分別取H=90R和W=30R,目前計算區域的尺寸遠大于文獻[37]的尺寸．氣泡距底壁的距離為h=5R,以消除底部壁面對氣泡初始運動的影響．

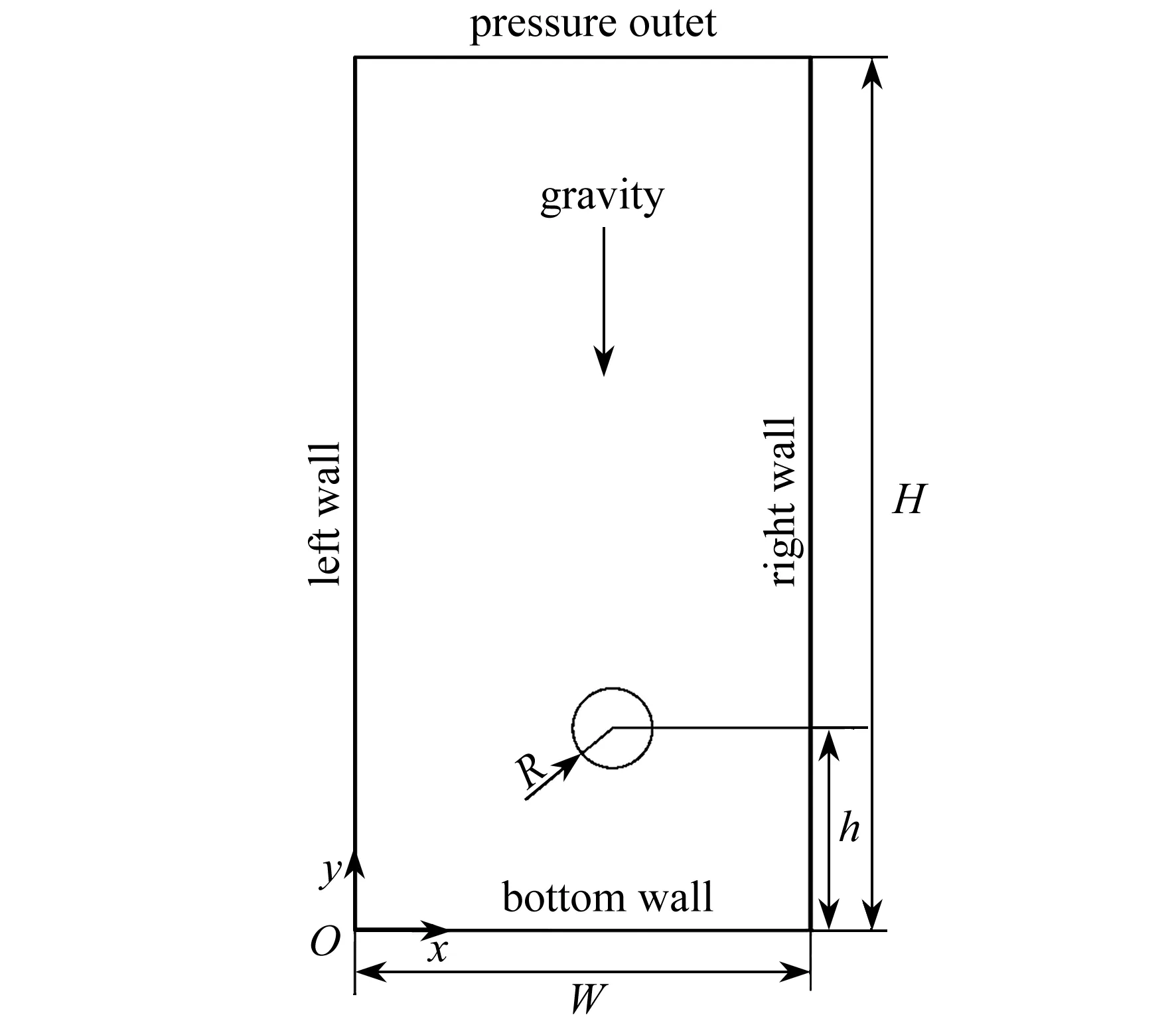
圖1 計算模型Fig.1 The computation model

1.2 控制方程

目前的計算是在層流、恒溫且氣液兩相均不可壓縮的前提下進行的,流體的控制方程有連續性方程和動量方程,具體如下:

?·u=0,

(1)

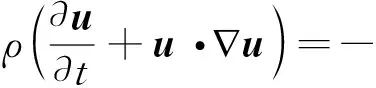
(2)

式中u為速度(m/s),p為壓力(Pa),ρ為流體平均密度(kg/m3),t為時間(s),Ds為黏性應力張量,Dp為彈性應力張量,Fs為表面張力源項,g為重力加速度(m/s2)．Ds和Dp的表達式如下:

(3)

(4)

式中μ為流體平均黏度(kg/(m·s)),μp為聚合物的黏度(kg/(m·s)),Cij為柔性高分子聚合物或表面活性劑分子的構象張量,xi為坐標(m),λ為聚合物松弛時間(s),δij為Kronecker符號(i=j時值為1,否則值為0),f(r)為Perterlin函數,即

(5)

(6)

式中L為聚合物分子拉伸長度與平衡長度之比,r為聚合物分子的理想長度．

構象張量Cij的輸運方程為

(7)

(8)

1.3 界面捕捉方法

使用VOF法捕捉氣液相間的界面,VOF法適用于兩種或多種互不相容的流體,通過引入一個或多個體積分數變量來區分各相,在每個控制體中,所有相的體積分數之和為1．當計算區域的位置與體積分數已知時,流體的熱物性參數表示為所有相的體積平均值．流場中相分布可以用相函數F表示,其被定義如下:

(9)

流體平均密度ρ和黏度μ均是氣液相的體積分數平均值,即

ρ=ρL(F)+ρG(1-F),

(10)

μ=μL(F)+μG(1-F),

(11)

式中ρL為液相的密度(kg/m3),ρG為氣相的密度(kg/m3),μL(=μs+μp)為液相的黏度(kg/(m·s)),μG為氣相的黏度(kg/(m·s)),μs為溶劑的黏度(kg/(m·s)),μp為聚合物的黏度(kg/(m·s))．

VOF法通過求解體積分數(或相函數)輸運方程來跟蹤界面,方程如下:

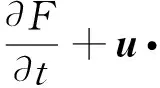
(12)

界面采用Youngs[42]提出的分段線性法(PLIC)進行重構,重構后的界面不是連續的．因此為了保證計算精度,對網格大小有嚴格的要求．

1.4 表面張力模型

表面張力采用Brackbill 等[43]提出的連續表面力模型(CSF)計算,氣泡表面的力可以用散度定理表示為體積力,將體積力作為源項加入動量方程(2)中,源項Fs表示為

(13)

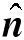
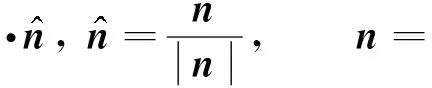
(14)

1.5 邊界條件和數值方法

在圖1所示的矩形計算區域中,上壁面設置為壓力出口邊界條件,左、右和下壁面均設置為無滑移壁面．由于結構化網格具有網格質量好、數據結構簡單且容易實現區域邊界擬合等優點,所以采用結構化網格對整個計算區域進行網格均勻劃分．梯度項使用基于網格中心的最小二乘法進行離散;動量方程采用二階迎風格式進行離散;壓力項采用PRESTO! (pressure staggering option)方法離散;體積分數采用幾何重構法求解．時間上的推進采用一階隱式格式,壓力和速度場的耦合選用SIMPLE算法．當氣泡形狀和上浮速度基本不隨時間變化時,計算視為收斂．所有參數設置完成后進行混合初始化,然后在計算域中加入氣泡,開始兩相流的計算．

1.6 計算條件和工況設置

為了研究氣泡在黏彈性流體中的上浮特性,控制液氣密度比為ρL/ρG=1 000和液氣黏度比為μL/μG=100,分別研究了Galileo數(Ga)、Weissenberg數(Wi)、Eotvos數(Eo)和黏度比(β)對氣泡運動的影響．Wi表征聚合物松弛時間與對流時間尺度的比值,Ga表征重力與黏性力的比值,Eo表征重力與表面張力的比值,β是溶劑和溶液的黏度比,分別定義如下:

(15)

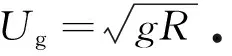
表1 計算工況Table 1 Design of the computation case

2 結果分析和討論

2.1 網格尺寸與時間步長的確定

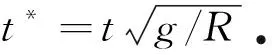
2.2 結果可靠性驗證

為了確保計算的可靠性,本文將參數為Ga=1.95,Eo=1,Wi=1和β=0.8時的計算結果與文獻[37]的結果進行了對比．圖4(左側為當前結果,右側為文獻[37]結果)對比了氣泡的形狀,可以看出氣泡形狀高度吻合．圖5對比了氣泡的上浮速度,時間和速度按照文獻[37]進行了無量綱化處理(t*=t/(R/Ug)和v*=v/Ug)．從圖中看出,氣泡穩定后的上浮速度分布基本一致,加速階段存在輕微的差異,或許是因以下原因造成的:① 本文使用的是二維模型,文獻使用的是三維模型;② 文獻對構象張量進行了對數化處理以處理高Weissenberg數帶來的數值問題．總而言之,目前的計算方法是可信的,可以開展目前的研究工作．

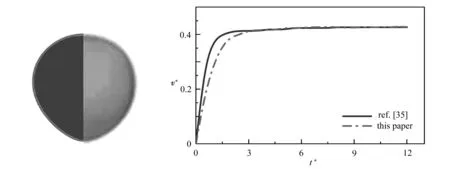
圖4 氣泡形狀對比 圖5 氣泡上浮速度對比Fig.4 Comparison of bubble shapes Fig.5 Comparison of bubble center velocities

2.3 氣泡變形分析

氣泡形狀會直接影響周圍液相流場的分布,進而對相間的傳質傳熱效率產生影響．為此,首先分析了各參數對黏彈性流體中上浮氣泡形狀的影響．圖6給出了黏度比β=0.2時,氣泡上浮運動穩定后的形狀．對應不同的參數,氣泡呈現為圓形、橢圓形、帽形(破碎和未破碎)、倒置淚滴狀以及其他不規則形狀．隨著Ga數的增大,氣泡從圓形向帽形轉變,并逐漸趨于扁平狀．當Ga=2,在低Wi數和低Eo數時,氣泡保持為圓形;當Eo數增大時,由于表面張力的減小,氣泡底部受向上射流的影響發生了輕微的上凹;當Wi≥0.5時,氣泡在低Eo數下,圓形氣泡底部在彈性力的拉伸作用下變長,隨著Eo數的變大,氣泡下部形成一個帶尖的尾部(所謂的“尾緣尖”),最終呈現為倒置的淚滴狀．當Ga=4時,氣泡形狀總體變得扁平(與Ga=2時相比),而且高Wi數下的“尾緣尖”現象消失;在較大Eo數下,出現了帽形氣泡．隨著Ga數的進一步增大,當Ga=8時,氣泡變得更加扁平;且在Eo=100時,氣泡底部出現了破碎現象,形成了許多衛星氣泡．當Ga=16,在Eo=1時,出現了非穩態氣泡,氣泡呈不規則形狀,上浮路徑為“之”字形;隨著Eo數的增大,氣泡破碎加劇．Wi數的大小表征了液體黏性和彈性的相對強弱．對于目前的研究,當Wi=0.1時,液相的彈性相對較弱,氣泡變形與在純黏液體中的變形相似．隨著Wi數的增大,液相的彈性增強,因此氣泡受液相彈性應力的影響變得明顯,當Ga=2時,氣泡形狀呈現出尾緣尖特征．隨著Eo數的增大,即表面張力的減小,氣泡保持原有形狀的能力變弱,氣泡形狀從橢圓形向尾部破碎的帽形轉變．

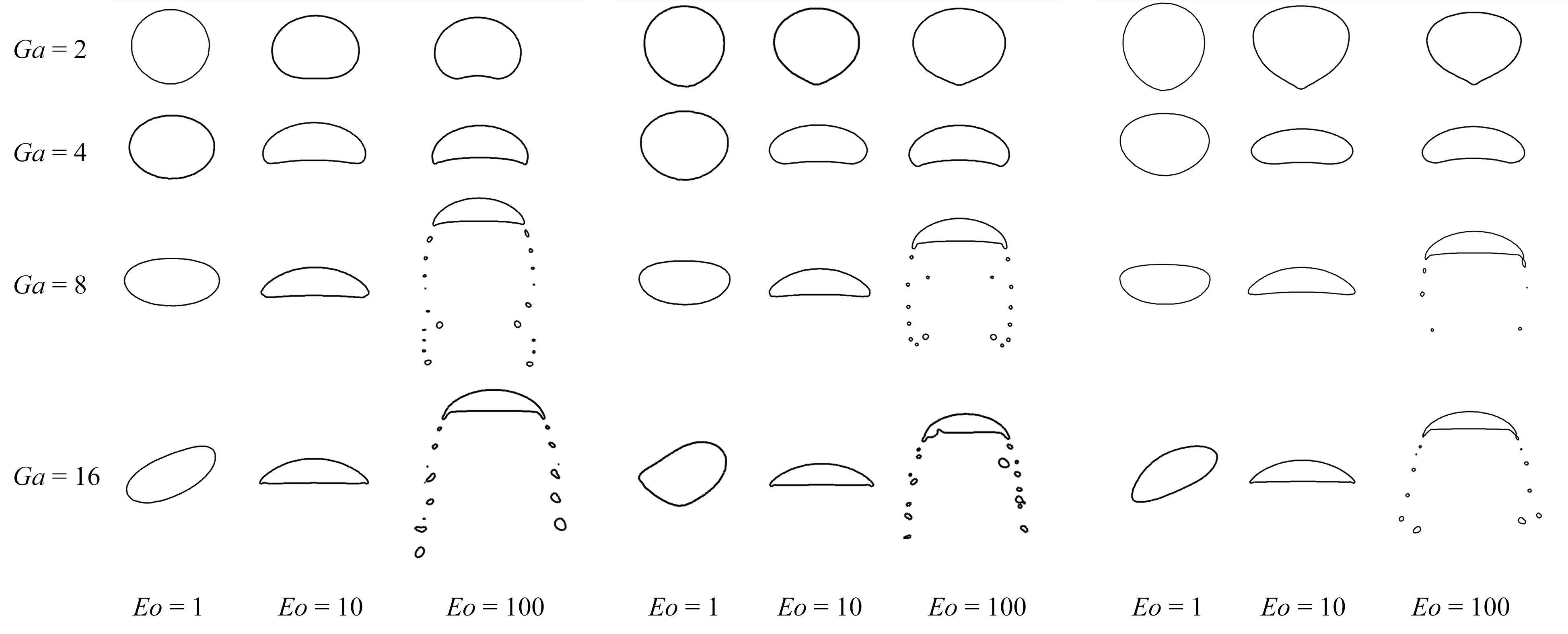
(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1圖6 β=0.2時,氣泡形狀隨Ga數,Wi數和Eo數的變化Fig.6 Bubble shapes against Ga,Wi and Eo numbers at β=0.2

為了理解黏度比對氣泡形狀的影響,圖7給出了Eo=10時,黏度比β=0.2,0.5,0.8下,氣泡形狀隨Ga數和Wi數的變化．結合圖6可以看出,隨著黏度比β的增大,原本出現“尾緣尖”的工況,氣泡變形為帽形．這是因為隨著黏度比β的增大,聚合物的黏度變小,液相的彈性變弱而黏性增強,即液相施加在氣泡上的黏性力變大而彈性力變小．所以氣泡變形與小Wi數的工況相似,類似于在純黏流體中的變形．

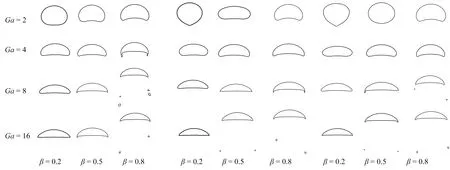
(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1圖7 Eo=10時,氣泡形狀隨β,Ga數和Wi數的變化Fig.7 Bubble shapes against β,Ga and Wi numbers at Eo=10

為了理解氣泡在黏彈性流體中出現的“尾緣尖”現象,給出聚合分子與氣泡作用示意圖(圖8)．氣泡受浮力作用向上運動時,由于黏性的影響會拖動氣泡周圍的液體一起向上運動,表征液相彈性的聚合物分子會受到拉伸．當聚合物分子被拉伸到一定程度時,會恢復至平衡態(類似于彈簧),這時液相中會產生一個與氣泡運動相反的力,也就是所謂的彈性應力．當彈性應力足夠大時,會通過黏性作用將力施加到氣泡表面上,該力最終作用在氣泡底部正中間,所以該區域受拉力的作用變形最明顯,形成“尾緣尖”．

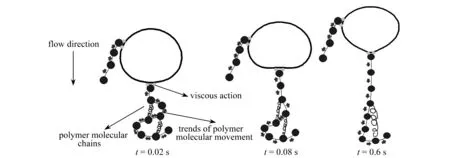
圖8 Wi=1和Ga=2時,聚合物分子對氣泡變形的影響Fig.8 Schematic of effects of polymer molecules on bubble deformation at Wi=1 and Ga=2

另外,對于Eo=1和Ga=16所有的工況,氣泡形狀和運動均極不規則(所謂的非穩態氣泡),氣泡沿“之”字形路徑上浮．這是因氣泡兩側尾渦周期性的脫落,在氣泡左右兩側產生了周期性的升力引起的．文獻[18,43-44]的實驗研究也發現了類似的現象．

2.4 氣泡上浮速度分析

氣泡的上浮速度(指氣泡內所有節點的平均速度)是研究氣泡水動力學的一個重要參數,氣泡的上浮速度在一定程度上影響了液相的含氣率,含氣率的高低會影響液相的表觀黏度和相間的傳遞效率[45-46],所以研究氣泡的上浮速度非常必要．為了研究彈性力和表面張力對氣泡上浮速度的影響,圖9給出了Wi數和Eo數對氣泡上浮速度的影響．從圖中可以看出,當Eo=1時,隨著Wi數的增大,氣泡上浮速度隨之增大．對應圖6給出的氣泡形狀可知,上浮速度增大的原因可能是在彈性應力作用下,氣泡下半部分受到拉伸,氣泡尾部變尖,氣泡整體形狀更接近于流線型,邊界層不易分離,氣泡上升過程受到的形狀阻力較小．當Eo=10和100時,Wi數對氣泡上浮速度的影響不明顯,這是因為氣泡形狀均呈現為帽形,橫向尺寸相似,所以氣泡受到的形狀阻力也相似,導致上浮速度變化不大．另外,在相同的Wi數下,隨著Eo數的增加,氣泡上浮速度先快速減小,然后緩慢減小．這是由于氣泡的形狀先由圓形變為帽形、最終近似穩定為帽形,導致阻力先快速增大然后趨于穩定引起的．

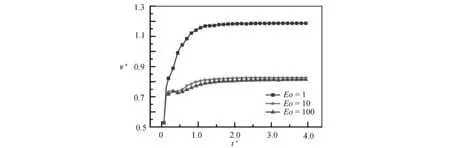
(a) Wi=1

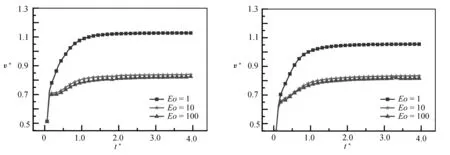
(b) Wi=0.5 (c) Wi=0.1圖9 Ga=4和β=0.2時,Wi數和Eo數對氣泡上浮速度的影響Fig.9 Effects of Wi and Eo numbers on the bubble rise velocity at Ga=4 and β=0.2

圖10給出Ga數對氣泡上浮速度的影響(Eo=10,β=0.2)．當Wi=0.1和0.5時,隨著Ga數的增大,穩定后氣泡的上浮速度隨之增大．這是由于隨著Ga數的增大,在重力保持不變的情況下,氣泡受到液相的黏性阻力減小引起的．在較大的Ga數(Ga=16)下,由于氣泡前一時刻的破碎,導致氣泡上浮速度在穩定前出現了一個峰值．當Ga數較小(如Ga=2)時,氣泡上浮速度隨Wi數的變化表現出一定的差異．當Wi=1時,氣泡經歷了一個“加速-減速-再加速”的過程,最后氣泡上浮速度超過相同工況下黏度較小(即Ga數較大)的工況．第一階段氣泡的加速是因浮力作用引起的;第二階段的減速是因氣泡底部受到射流的作用、發生上凹變形,變形成帽形,氣泡的形狀阻力增大,所以出現了減速現象;第三階段的加速是因液相中聚合物分子的彈性拉伸,氣泡底部受到聚合物恢復至平衡態向下的彈性拉力,氣泡從帽形變為“倒置的淚滴”狀,形狀阻力又減小,所以氣泡的上浮速度又增大．因氣泡形狀最終穩定在阻力最小的狀態,所以氣泡速度高于低黏度工況下的速度．氣泡的變形過程如圖8所示．

(a) Wi=1

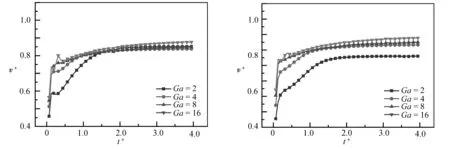
(b) Wi=0.5 (c) Wi=0.1圖10 Eo=10和β=0.2時,Ga數對氣泡上浮速度的影響Fig.10 Effects of the Ga number on the bubble rise velocity at Eo=10 and β=0.2

另外,從圖9可以看出,當其他條件相同,Eo=1時,氣泡上浮過程沒出現再加速現象,而是一次性加速達到穩定的峰值;但Eo≥10時,氣泡速度出現了輕微的波動．這說明形狀阻力的變化是導致氣泡出現再次加速的主要原因．Niethammer等[47]報道過類似的現象,他們認為第一階段氣泡的加速是因浮力驅動引起的,這與本文一致,而第二階段氣泡的減速,則被歸因于氣泡表面彈性應力層足夠大以至于對氣泡運動產生了影響,對于第三階段氣泡的加速他們認為當氣泡體積大于臨界體積時,氣泡赤道下方的環向彈性應力引起氣泡再次大幅加速[48]．

圖11展示了黏度比β對氣泡上浮速度的影響(Ga=2,Eo=10)．當Wi=1時,隨著黏度比的變大,氣泡上浮速度明顯減小．這是因為黏度比β的增大導致黏性力作用增強而彈性力的作用減小,導致氣泡受到的黏性阻力增大,所以上浮速度變小．通過對比圖中β=0.2所有的工況可以看出,上文中提到的“加速-減速-再加速”現象隨著Wi數的增大而變得明顯．這足以說明彈性力對氣泡形狀和上升速度的影響非常大．

(a) Wi=1

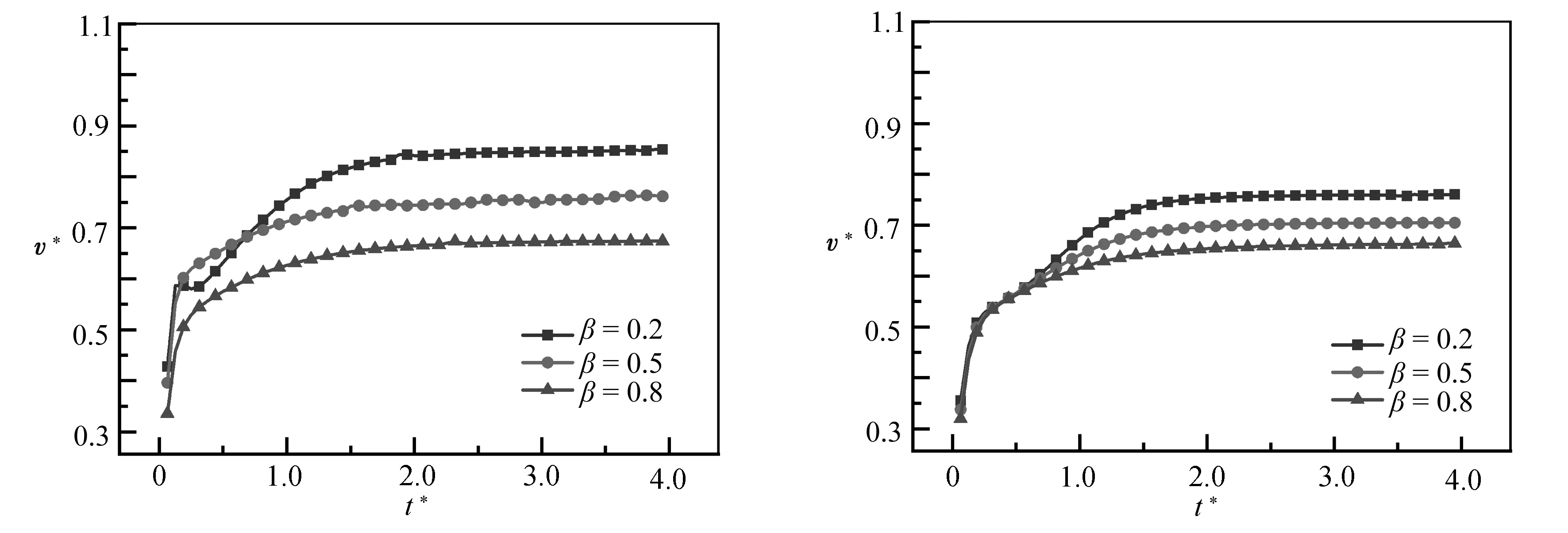
(b) Wi=0.5 (c) Wi=0.1圖11 Ga=2和Eo=10時,黏度比β對氣泡上浮速度的影響Fig.11 Effects of viscosity ratio β on the bubble rise velocity at Ga=2 and Eo=10

綜合對比圖9—11可以發現,氣泡在黏彈性液體中上浮時,氣泡上浮速度隨時間的變化表現出現“持續加速到穩定”和“加速-減速-再加速到穩定”兩種形式,這不同于氣泡在純黏流體中的現象,說明了彈性的影響非常顯著．氣泡在純黏流體中上浮時,普遍會出現“加速-減速-(某些條件下)輕微再加速”,最后取得穩定的終端速度[37],這種速度波動是因浮力和阻力之間的動態平衡引起的．對于黏彈性流體中“持續加速到穩定”現象是因下述原因引起的,即當彈性較弱(Wi=0.1)和表面張力較大(Eo≤10)時,氣泡變形輕微,既不會因射流作用尾部迅速上凹,也不會因為彈性力作用呈現“尾緣尖”,此時浮力與氣泡阻力之間動態平衡產生的速度波動現象因彈性力的存在變得不明顯．當彈性較強(Wi≥0.5,β=0.2),黏度較大(Ga=2)和表面張力較弱(Eo≥10)時,氣泡底部出現“尾緣尖”導致形狀阻力大幅減小,從而出現了明顯的再次加速．第二階段減速現象仍存在的原因是,當彈性聚合物松弛時間較大時,彈性應力的釋放存在一定的延遲,氣泡底部受射流的影響仍會存在上凹的歷程．

2.5 氣泡尾渦分析

為了進一步分析氣泡在黏彈性流體中的水動力學特性,下面給出了氣泡的尾渦分布圖．圖中紅線表示氣泡的邊界輪廓．對于所有的工況,氣泡內部都形成了兩對對稱的渦,一對較大,另一對較小．為了理解各參數對氣泡尾渦分布的影響,圖12給出了Ga=4和β=0.2時,Wi數和Eo數對氣泡尾渦的影響;圖13給出了Eo=10和β=0.2時,Ga數和Wi數對氣泡尾渦的影響．

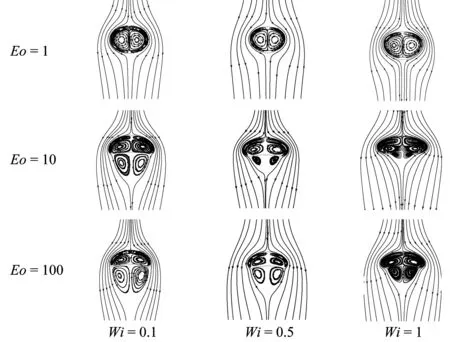
圖12 Ga=4和β=0.2時,Eo數和Wi數對氣泡尾流的影響Fig.12 Effects of Eo and Wi numbers on the bubble wake at Ga=4 and β=0.2

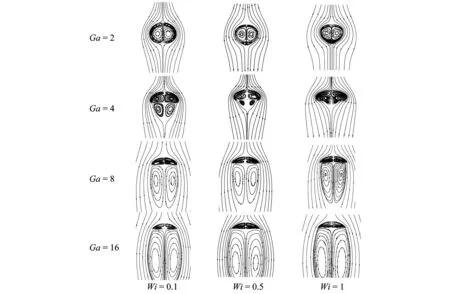
圖13 Eo=10和β=0.2時,Ga數和Wi數對氣泡尾流的影響Fig.13 Effects of Ga and Wi numbers on the bubble wake at Eo=10 and β=0.2

從圖12中可以看出,當Wi數相同,在Eo=1時,由于氣泡變形較小,氣泡尾部沒有尾渦生成．這是因氣泡形變小(界面曲率大且變化小),在氣泡界面產生的渦量較小,很快被來流帶走,不會聚集在氣泡尾部．當Eo=10和100時,氣泡形變明顯、呈現為帽形,界面曲率變化大且流動阻力(主要是形狀阻力)使氣泡上下側的壓差變大,導致了尾渦的出現,且隨著Eo數的變大,尾渦被逐漸拉長．當氣泡形變成帽形時,尾渦的出現導致氣泡的上浮速度大幅減小．從圖13可以看出,當其他參數相同時,隨著Ga數的增大氣泡尾渦明顯增大．隨著Wi數的增大,氣泡的尾渦尺寸變小,這是因為彈性力在一定程度上能夠阻止氣泡形變為帽形,減小氣泡的形狀阻力．這也進一步解釋了氣泡上浮速度隨著Wi數的增大而增大的原因．

2.6 氣泡周圍正應力分析

因聚合物正應力τyy云圖在一定程度上能體現氣泡周圍聚合物濃度和彈性應力的作用效果,而且通過觀察正應力云圖可以更直觀地理解彈性應力的作用規律．為此,給出了液相的正應力τyy分布云圖(圖14)．

(a) Wi=0.1 (b) Wi=0.5 (c) Wi=1圖14 β=0.2時,τyy分布云圖Fig.14 At β=0.2,contour plots of τyy

從圖14可以看出,大正應力區主要集中在氣泡尾部和氣泡赤道位置附近,這些區域也是剪切較強的區域,這也再次證明彈性應力對氣泡變形的影響不容忽視．當其他參數相同時,隨著Wi數的增大,正應力的大小和作用范圍總體上表現出增大的趨勢．前文提到彈性應力使氣泡尾部受到拉伸,氣泡形狀趨于流線形,從而導致上浮速度增大．從正應力云圖來看,大彈性應力出現在氣泡赤道附近,分析對應位置處的流線不難看出,當氣泡上浮時,氣泡頂部和周圍的液體向赤道位置匯聚,導致氣泡表面附近存在較大的速度梯度,所以形成較強的剪切作用．受剪切的影響,氣泡赤道附近聚合物分子被向下拉伸,從而在氣泡上產生一個向上的彈性應力,也可使氣泡上浮速度變大,如圖8所示．當其他參數相同,改變氣泡的Eo數時,氣泡的形狀隨之變化,導致正應力的大小和位置也發生變化．當Eo數較小時,氣泡變形較小,大正應力區域主要出現在氣泡兩側偏上和尾部區域;當Eo數較大時,氣泡變成帽形,大正應力區域逐漸移動到帽形的裙邊處;當氣泡出現破碎時,大正應力區域分布在脫落氣泡的周圍,也出現了大應力區域脫落的現象．對于大Ga數的工況,正應力作用區域相對變大,但大應力區域減小．一方面是聚合物黏度減小的原因;另一方面是小黏性力的作用導致氣泡上浮速度較大,在聚合物分子松弛時間不變的前提下,在聚合物分子單次拉伸恢復至平衡態所需的時間內,氣泡上浮了更遠的距離,從而導致正(彈性)應力作用區域變大．

3 結 論

本文基于Oldroyd-B黏彈性模型,運用VOF法模擬了氣泡在黏彈性流體中的上浮運動．再現了氣泡在黏彈性流體中呈倒置淚滴形狀的現象,解釋了該現象產生原因,并詳細分析了Ga數、Eo數、Wi數和黏度比β對氣泡形狀和上浮速度的影響．主要結論總結如下:

1) 氣泡在黏彈性流體中上浮時,可呈現為圓形、橢圓形、帽形(破碎和未破碎)、倒置淚滴狀和其他不規則形狀．隨著Ga數和Eo數的增大,黏性力和表面張力減小,氣泡變形程度增加;在大Wi數和小黏度比β下,彈性較強,氣泡底部受到強烈的拉伸作用; 在小Wi數和大黏度比β下,彈性較弱,氣泡形狀與純黏流體中的相似．當Ga=16和Eo=1時,氣泡受到周期性升力的作用表現出非穩態形狀; 當Ga=2,Wi≥0.5和β=0.2時,氣泡尾部出現了大小不同的“尾緣尖”,該現象是彈性力、黏性力、表面張力和慣性力綜合作用的結果,而彈性力是“尾緣尖”現象的必要條件．

2) 氣泡在黏彈性液體中的上浮速度普遍大于在純黏液體中的速度．與純黏流體不同,氣泡在黏彈性流體中上浮時,氣泡上浮速度有持續加速到終端速度和加速-減速-再加速到終端速度兩種形式,后者的再加速現象是因氣泡“尾緣尖”的出現導致氣泡所受形狀阻力減小引起的．

3) 當氣泡變成帽形時,因氣泡上下兩側壓差較大且界面曲率變化較大,在氣泡尾部出現了尾渦,氣泡尾渦隨著Eo數的增大而拉長．τyy大應力區主要集中在氣泡尾部和赤道處;隨著Wi數的增大,聚合物松弛時間變長,且氣泡將聚合物分子拉伸長度變大,所以彈性應力作用范圍變大．

致謝本文作者衷心感謝常州大學“SIETP”基金項目(2022-C-06)對本文的資助．