滲透類比思想 培養創新思維
——以“等比數列及其通項公式”為例

江蘇省西亭高級中學 (226300) 丁建兵

當下,數學教育側重于方法、過程和個體體驗,關注于學生自主學習能力和創新能力的提升.因此,在數學教學中,單一的知識講授已經難以滿足學生生長和思維發展的需求.教學中,教師有必要采用多種的教學方式和教學手段來提升學生的數學思維能力,以此提升學生的數學水平.類比思想方法在提高學生自主學習能力,激發學生潛能,發揮學生主體性等方面有著重要的應用.因此,教師應結合教學實際,創造機會引導學生通過新舊類比來理解和掌握新知,幫助學生建立完整的知識網絡.筆者以“等比數列及其通項公式”為例,呈現類比思想在教學中的應用價值,以期通過類比提高學生的數學探究能力和創新能力.

一、教學分析

1、教學目標

(1)理解等比數列的定義及相關概念;

(2)掌握等比數列的通項公式,并運用通項公式求相關項;

(3)運用類比思想方法提高學生觀察、歸納、分析等邏輯思維能力,提高學生數學學習水平.

2、教學重難點

(1)等比數列的定義及通項公式、等比中項等相關概念;

(2)等比數列通項公式的推導.

二、教學簡錄

1、導入

問題已知數列{an},其中a1=1,a2=2;數列{bn},其中b2=2.對任意的i、j、m、p∈N*,i+j=m+p,均有aibj=ambp,試求{an}與{bn}的通項公式.

問題給出后,教師讓學生嘗試運用等差數列的學習經驗尋找解決問題的方法.

師:通過研究問題,你有什么發現?

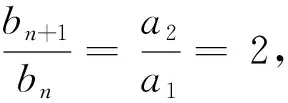
師:很好,結合等差數列的學習經驗,你認為我們應該如何來描述它的本質屬性呢?它的通項公式又會是什么呢?

設計意圖：借助問題讓學生發現所研究的內容與之前所學不同,由此引發學生對新知探究的熱情.同時,教師有意識引導學生聯想等差數列,繼而為類比教學作鋪墊.

2、探索新知

環節1:探索定義

師:等差數列的定義大家還記得嗎?

生齊聲答:記得.

教師點名讓學生陳述等差數列的定義.

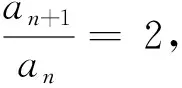
在教師的啟發和引導下,學生給出了等比數列的定義,教師進行補充,并給出等比數列的完整定義.

設計意圖：引導學生與等差數列的定義相類比,抽象等比數列的本質屬性,以此提高學生的抽象概括能力,激發學生探究熱情.

環節2:探索通項公式

師:與等差數列的定義相比,你認為等比數列強調的是什么呢?(生積極思考)

生2:等比數列的任意項不能為0,即公比q不能為0.

生3:也就是說常數列一定是等差數列,但是它不一定等比數列,如0,0,0,….(生3補充道)

師:大家說得很好.那么對于問題1中的數列{an},它的通項公式會是什么呢?

在教師的啟發和引導下,學生結合等差數列公式的推導經驗,利用累乘的方法推導出等比數列的通項公式為an=a1qn-1.

這樣完成等比數列概念的抽象和通項公式推導后,教師鼓勵學生與等差數列相類比,并用列表方式進行小結.通過師生互動交流,教師給出下表:

在表1的基礎上,進一步分析,從運算符號上進行總結歸納,從而得到了表2:

表1

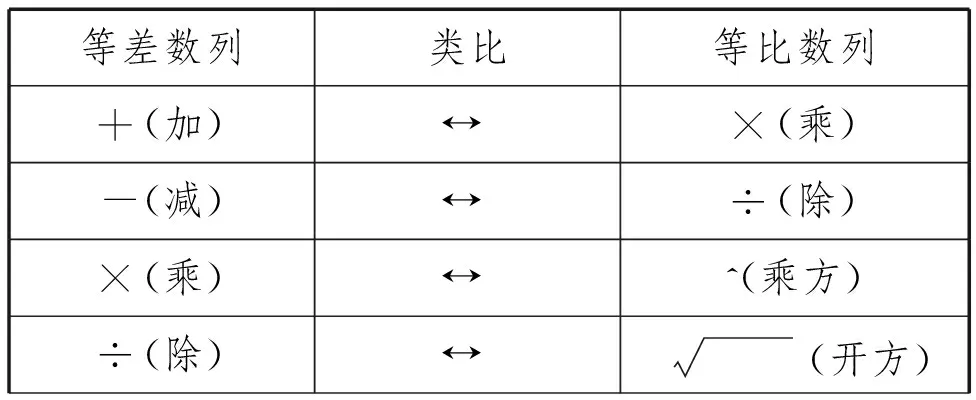
表2

設計意圖：教師充分發揮學生的主體性,引導學生進行對比分析,這樣既幫助學生鞏固了已有的等差數列的相關知識和經驗,又讓學生在自主探索中獲得了新知.另外,在此環節,教師刻意放慢節奏,引導學生利用表格對比總結等差數列和等比數列的差異,讓學生在理解知識的基礎上,掌握數學研究方法,提升了學習質量.

環節3:探索性質

師:在學習等差數列時,我們還學習了等差中項,你認為等比中項會是什么呢?(生積極交流)

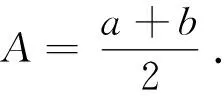
學生通過類比聯想得到等比中項的概念后,教師指導學生進行科學驗證.在此基礎上,教師給出相應練習讓學生進一步理解相關概念,并得到相關結論.

師:很好,若求9和25的等差中項A和等比中項G該如何求呢?

學生根據中項公式很快得到等差中項A是17,等比中項G是15或-15.

師:若數列{an}為等比數列,其中a1=9,a5=25,求a3的值.

問題給出后,部分學生結合上面解題經驗給出a3的值為15或-15,顯然部分學生掉入了教師預設的陷阱,由此教師充分利用這一生成讓學生思考:這里為什么a3不能為負值.

師:結合以上問題,你能得出什么結論嗎?

生5:在等比數列{an}中,其奇數項{a2n-1}和{a2n}各項的符號相同.

設計意圖：教師從學生已經掌握的等差數列出發,通過類比聯想讓學生推理相關結論,以此提高學生學習能力,提升學生數學核心素養.

3、練習(略)

三、教學思考

等差數列和等比數列是高中的重要內容,也是高考的重要考點,兩者既有明顯的聯系,也有一定的區別.在教學等比數列時,大多教師會從等差數列入手,開展類比教學,以此在鞏固舊知的基礎上讓學生自主抽象相關的概念及性質,以此提高學生的邏輯思維能力,落實學生數學核心素養.

1、問題引領,引發類比

在本案例教學中,教師從學生熟悉的等差數列練習題入手,通過改編將問題轉化為等比數列,由此引發認知沖突,既激發了學生的探究欲,又為本課開展類比學習埋下伏筆.在探索新知的過程中,教師鼓勵學生運用類比方法進行探索,如在給等比數列下定義時,教師引導學生回顧等差數列的定義,然后通過類比抽象出等比數列的概念.當然,在以上教學中,除了引導學生進行知識方面的類比外,教師還重視引導學生關注方法的類比.如在推導通項公式時,教師引導學生從累差法入手,通過對比分析,自然發現累乘法,從而推導出等比數列的通項公式.通過類比提高了學生認識問題和解決問題的能力,提高了課堂教學有效性.

2、科學驗證,求同存異

類比是一種重要的數學思想方法,它可以幫助學生在已有知識、經驗的基礎上進一步拓展延伸,以此培養學生的創造性思維,激發學生的創造潛能.不過類比得到的結論是一種猜想,具有一定的主觀性,需要進行科學的驗證.

例如,在探究等比中項時,不能想當然地認為等比中項與等比數列是充要條件,如0,0,0不是等比數列,但是02=0×0.因此,在教學中,既要“求同”,啟發和引導學生發現知識間的內在聯系,達到溫故知新的效果,也要“求異”,指導學生對結論進行驗證,從而有效避免形式上的類比而出現負向遷移.

總之,在高中數學教學中,教師要不斷更新教學觀念,引導學生關注知識的形成過程,有效地提升學習質量和學習效率.