夯實基礎強本質,彰顯能力重創新*
——基于“三新”背景下的三角函數大單元的深度學習

陜西省安康市漢陰中學 (725100) 梁 華

在新教材(人民教育出版社2019年國家教材委員會專家委員會審核通過)、新課程(《普通高中數學課程標準(2017年版,2020年修訂》)、新高考的“三新”背景下,三角函數模塊知識試題的命題具有明顯的特點,更注重數學知識的基礎性、網絡性,夯實基礎;凸顯數學知識的綜合性、聯系性,強化本質;展示數學思維的靈活性、應用性,彰顯能力;強調數學意識的探究性、創新性,側重創新等,更強調結合三角函數自身以及三角函數與其他知識之間的聯系,充分體現高考數學的考查效能、選拔功能及高考的區分功能．

1．夯實基礎,構建網絡

“三新”背景下三角函數的命題,突出對三角函數的概念與定義、圖象與性質、基本公式等層面的考查,全面構建三角函數的知識網絡,注重三角函數的基礎知識的理解與掌握,全面夯實基礎．

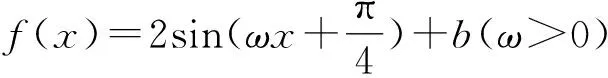
A．ω=2 B．f(x)的值域是[-2,2]

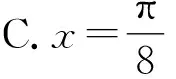
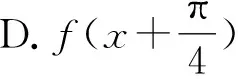
分析：根據題設條件,通過函數f(x)的周期滿足的不等式以及對稱中心,構建相關參數的不等式或關系式,得以確定對應的參數值,進而確定三角函數的解析式,利用三角函數的圖象與基本性質來分析與判斷．

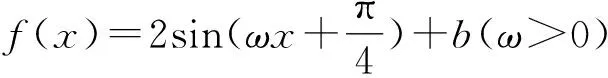
綜上,本題選擇A、C．

點評：三角函數的圖象與基本性質是解決相關三角函數問題中的基礎所在,也是高考三角函數模塊中的根本．解決此類問題的關鍵就是利用題設條件確定對應的參數值,正確構建對應的三角函數解析式,為進一步的綜合與應用提供條件．

2．強化本質,增加聯系

“三新”背景下三角函數的命題,強化三角函數的本質屬性與內涵,注重三角函數與函數、三角函數與解三角形以及三角函數與其他知識之間的聯系,突出三角函數的自身應用以及其與其他知識的聯系,展示內涵本質．

例2 (2023屆臺州市高三數學一模題)設△ABC的三個內角A,B,C所對的邊分別為a,b,c．若A≠B,且sinAcos(2B-A)=sinBcos(2A-B)．則tanAtanB的值為________．

分析：根據題設條件,結合解三角形與三角函數的聯系,借助題設中的三角關系式,尋找關鍵角A-B進行整體思維,利用三角關系式合理配湊與巧妙轉化,結合三角恒等變換公式進行轉化與求解．

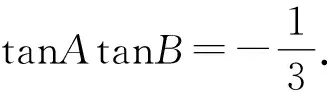
點評：三角函數與解三角形之間的綜合與聯系,是三角函數模塊知識中比較常見的一種聯系方式．此類問題中,關鍵是尋找角與角之間的關系,或單獨處理,或整體思維,特別是利用關鍵角的整體應用,往往是合理配湊與整體思維的巧妙應用,對于解決此類三角函數關系式具有很強的應用性、技巧性．

3．彰顯能力,凸顯思維

“三新”背景下三角函數的命題,熟練理解并掌握三角函數中的相關概念與公式,重視三角公式的應用,開拓三角函數的考查空間與思維角度,提升相應的認知水平與解題技巧,提升數學能力,凸顯數學思維．

例3 (2022—2023學年南京市高三(上)學情調研數學試題)已知函數f(x),任意x,y∈R,滿足f(x+y)f(x-y)=f2(x)-f2(y),且f(1)=2,f(2)=0,則f(1)+f(2)+…+f(90)=( ).

A．-2 B．0 C．2 D．4

分析：結合已知條件f(x+y)f(x-y)=f2(x)-f2(y)的結構特征,合理聯想到三角函數模型的正弦平方差公式sin2x-sin2y=sin(x+y)sin(x-y),合理配湊系數,構建特殊三角函數模型來進行特殊化處理．

點評：借助三角函數模型來特殊化解決此類問題時,往往是結合抽象函數的結構特征與對應的三角函數公式加以聯系,其中三角函數模型f(x)=Asinωx(A,ω≠0)或f(x)=Acosωx(A,ω≠0)中的最值情況由系數A決定,周期情況由系數ω決定,根據具體場景加以合理正確選取．

4．側重創新,強調意識

“三新”背景下三角函數的命題,結合三角函數與基本知識的交匯融合、三角函數的實際應用問題以及三角函數中的數學文化等問題的創設,合理創新與應用,有效增強數學思維與能力的綜合性、創新性,展示三角函數的創新應用,強調創新意識．

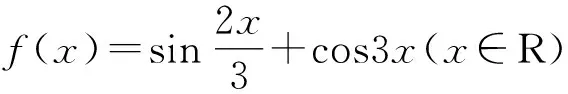
A．15π B．12π C．6π D．3π

分析：通過創新場景的類比,利用干支紀年歷法的規律,類比確定“加(減)”混合類的三角函數的最小正周期的求解,結合正弦型(或余弦型)函數的最小正周期的確定,并結合最小公倍數的確定來綜合與應用．

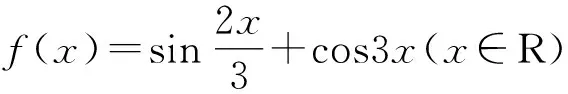
點評：在創新場景下,通過類比思維與類比創新,構建不同知識之間的鏈接,通過合理的推理與證明,實現數學文化知識與三角函數知識之間的關聯,形成數學思維的創新性、數學方法的創新性等．

在“三新”(新教材、新課程、新高考)背景下,進一步落實“雙減”政策與新改革理念,積極貫徹《總體方案》要求,高考三角函數知識模塊的命題特色在尋求基礎、本質、能力、創新等的基礎上,更多側重數學基礎與關鍵能力的考查,堅持開放創新與核心素養導向,更加注重數學創新意識與創新應用,全面體現高考的選拔性與區分度．