多頻帶聲學超構材料的透射性能

郝麗梅，楊 宵，閆小樂，程 紅，李育佳，王雅喆，解 憂

（西安科技大學 理學院，陜西 西安 710054）

0 引言

聲學超構材料是一種人工合成的周期性結構材料，它的結構尺寸遠遠小于材料的工作波長，具有很多奇異特性，如負等效模量［1］、負等效質量［2］和負折射率［3］等。重要的是它還可以控制聲波的傳播方向，近年來在聲隱身［4］、亞波長成像［5］、超透鏡［6］、反常多普勒效應［7］、超吸收［8］、聚焦［9］、振動隔聲［10］等方面有顯著的應用潛力。近20 a，聲學超構材料的研究受到人們的廣泛關注。

聲學超構材料的核心是設計人工微結構實現對聲波的有效調控。2000年，LIU等將鉛球包裹在硅橡膠中，該局域共振型結構可以等效為質量－彈簧模型，在400 Hz和1 350 Hz這2個頻率附近實現了聲透射阻帶和負等效質量密度［2］。YAO等基于質量－彈簧模型，設計丁苯橡膠填充鋼格柵彈性超材料實現不同頻帶的聲透射阻帶［11］。這些材料均采用局域共振型結構原理設計微結構單元實現負等效質量密度。2010年，YANG等將質量塊固定在張緊的薄膜上制得薄膜型聲學超構材料，在200～300 Hz實現了聲透射阻帶［12］。MEI等利用帶有多塊小板的薄膜，實現較寬頻的聲透射阻帶［13］。FAN等提出一種開孔薄膜的管狀一維聲學超構材料，在400～600 Hz附近出現透射阻帶［14］。LIN等設計一種橡膠薄膜型超材料，該薄膜可以看作是同時具有阻尼和彈簧雙重作用的負質量密度薄膜。薄膜型超材料表現出了其結構單元偶極共振的物理學特征［15］。

聲學超構材料的聲波傳輸調控依賴于結構單元的形態及參數變化，通常采用偶極共振模式［16］。目前，研究者們旨在優化超材料異構結構單元數目來實現多頻或寬頻的聲波透射調控及負質量密度。例如，LEE等利用多規格薄膜陣列表現出寬頻的聲透射阻帶［17］。YANG等通過將多個模板堆疊實現寬頻帶的聲透射阻帶［18］。CHEN等以同心環結構來構建二維單振子、雙振子和三振子帶有耦合作用的聲學超構材料，在多個頻段出現聲透射阻帶［19］。REN等提出一種輕質亞波長超薄多縫的結構，在降低系統整體質量的基礎上能夠在較寬的頻率范圍內吸收聲音［20］。FAN等提出了一種基于膜涂層穿孔板的聲學超構材料，以實現在低頻范圍內的隔音［21］。XU等提出一種雙層多孔薄板聲學超構材料，通過調節孔徑大小來調控聲透射阻帶的位置［22］。ZHAO等將很多不同長度的空心管組成雙層結構聲學超構材料，其中在介質分別為水和空氣的條件下，均實現了寬頻帶的聲透射阻帶［23－24］。通過增加額外質量結構單元的形式拓寬了聲學超構材料的響應頻帶，但存在制備復雜、應用不便等問題。

文中基于空心管結構［23－26］，將兩端均與介質連通的空心管優化為一端封閉一端連通的（OECE）空心方管，在薄的聲學板上內嵌OE－CE空心方管結構構建多頻帶聲學超構材料。采用聲學有限元方法（FEM）模擬多種嵌有OE－CE空心方管的聲學超構材料板，仿真研究不同空心方管數目對透射性能的影響規律。最后通過組合不同長度的空心方管設計出并聯型多頻帶聲學超構材料板。

1 模型構建

1.1 結構單元設計與模擬

將OE－CE空心方管并列組成聲學超構材料板單元，板內部嵌有多個空心方管，一側與空氣連通，另一側是封閉的薄壁，如圖1所示。OE－CE空心方管的初始結構參數設定為：邊長a1＝a2＝8 mm，薄壁厚度t＝1 mm，相鄰OE－CE空心方管的間距u＝2 mm。聲學薄板的幾何參數：長L1＝100 mm，寬L2＝90 mm，厚度d＝10 mm，這里的厚度僅有大約最短工作波長的八分之一，因此稱之為聲學薄板。

圖1 嵌有OE－CE空心方管的聲學薄板結構Fig.1 Structure of acoustic thin plane with OE－CE square hollow tube

在外界聲波的激勵下，OE－CE空心方管中的空氣在諧振頻率附近發生諧振，從而使得該結構單元呈現出負等效質量密度的聲學特性。

利用COMSOL Multiphysics的聲－結構模塊在頻域內對結構單元進行模擬計算。在波導管中，設置幅值為1 Pa的平面波從波導管一端入射，另一端設為匹配邊界，可實現波導管內聲波傳遞的完全吸收，避免聲波來回振蕩影響計算結果。4個邊界為周期性邊界條件，這時每個板可以被單獨看作一個在空間內無限衍生的單元結構。當聲波經過樣品時，通過4個不同的探測面采集對應處聲波的幅值和相位，利用傳遞函數法解耦得到透射系數T和反射系數R，再對其數據進行后處理得到等效質量密度等聲學參數。

在COMSOL仿真中，設置固體域材料為Steel AISI 4340，其余域為流體域，設置流體域材料為空氣，聲速為343 m／s，密度為1.29 kg／m3。

1.2 長度對結構單元透射性能的影響

為了探究空心方管長度L1對結構單元透射性能的影響規律，該部分以嵌有9個空心方管的聲學薄板為研究對象，選用能反映出諧振頻率隨空心方管長度L1變化規律的長度，即L1分別為30，40，50，60，70 mm，并利用Comsol仿真軟件對其進行仿真研究，最終得出不同長度聲學超構材料板的頻率－透射曲線（圖2（a））。

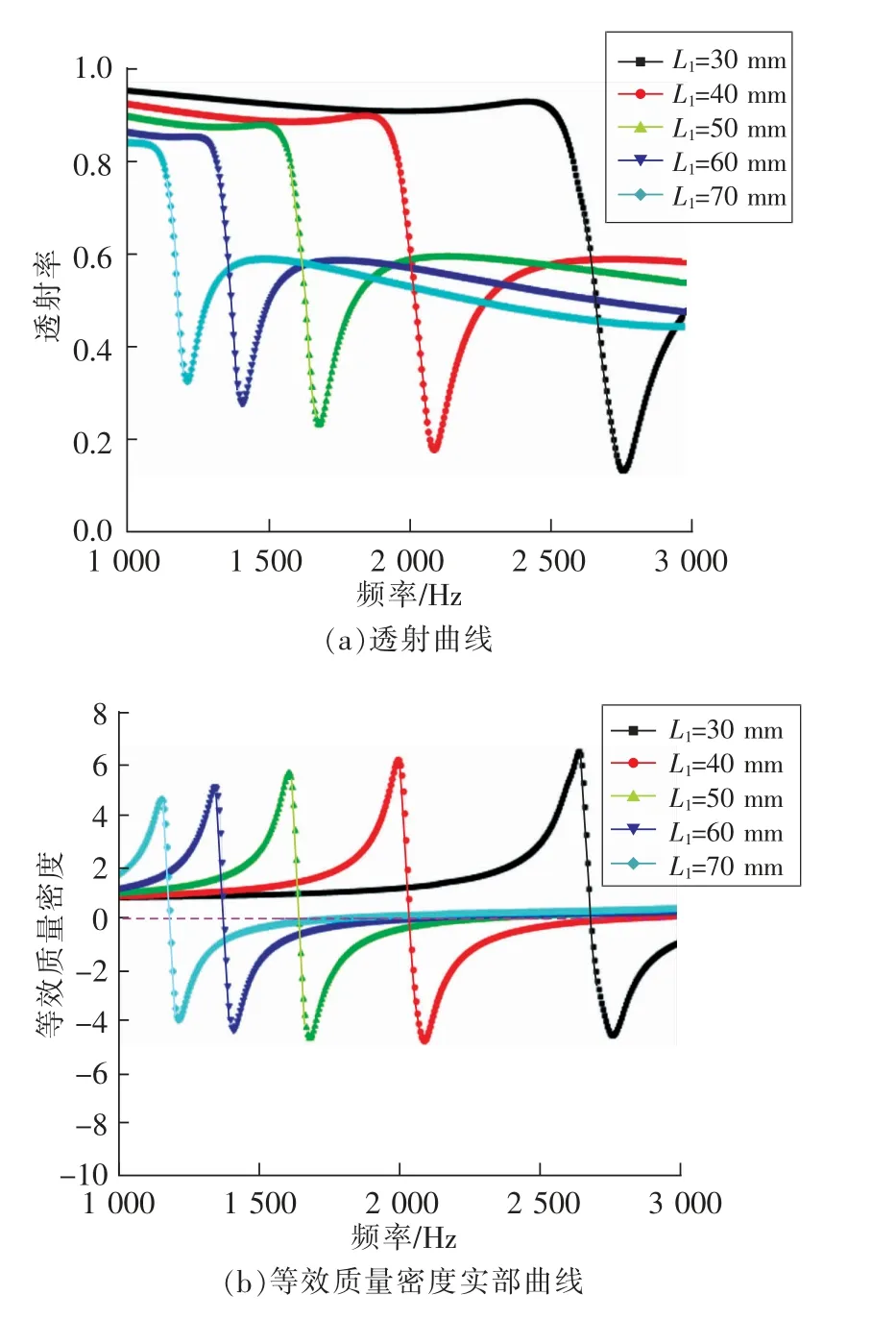
圖2 不同長度聲學超構材料板Fig.2 Acoustic metamaterial planes with different lengths

從圖2（a）可以看出，不同長度聲學超構材料板的透射譜中均出現一個明顯的透射阻帶。隨著空心方管長度的增加，透射阻帶出現紅移，且阻帶峰值逐漸升高。例如當L1分別為30，40，50，60，70 mm時，對應的聲學薄板諧振頻率分別為2 740，2 070，1 665，1 395，1 200 Hz，透射阻帶最低峰值分別為0.23，0.28，0.33，0.40，0.46。其中出現紅移現象的原因可能是：空心方管的長度增加，使得等效聲感（Leff∝ρL1／S）增加；同時管腔體積的增加引起等效聲容的增加。因此對應的諧振頻率降低［25］。

圖2（b）為不同長度聲學超構材料板的等效質量密度曲線。不同長度的情況下，空心方管的等效質量密度在各自的諧振頻率附近（即透射阻帶）均為負值。其原因可能是空心方管內存儲了大量聲能，其中的空氣柱以諧振頻率振動，而外界聲場驅動力與空氣柱加速度方向相反［23］。

2 結果與討論

當空心方管一端與空氣連通，另一端用薄壁封閉時，空氣柱只能在連通端進入空心方管，在管腔內來回振動。結合聲電類比方法分析，對比兩端都連通的空心管，OE－CE空心方管具有更高的電感，諧振頻率更低，選用OE－CE空心方管設計在低頻范圍內多頻帶聲學超構材料有較大的優勢。因此，文中主要研究不同長度OE－CE空心方管的數目對聲學超構材料板的頻帶個數的影響規律。

2.1 雙頻帶并聯型聲學超構材料的透射性能

對于由2種不同長度的空心方管并聯組合形成雙頻帶聲學超構材料，其薄壁厚度t為1 mm，薄壁將連通的腔體分割為2個獨立的OE－CE空心方管，板長L1為2種空心方管的長度之和（圖3）。

圖3 2種不同長度組合的聲學薄板結構Fig.3 Structure of acoustic thin plane with two different lengths

例如將40 mm和70 mm長度的空心方管進行組合，則聲學超構材料的板長L1為110 mm。其余參量和上一節相同。當板長L1的長度和薄壁位置發生變化時，空心方管的組合也隨之改變。

圖4為2種不同長度組合下的聲學薄板的透射曲線。由圖可知，5種不同組合的情況下，其透射曲線均出現2個透射阻帶，且相比于單獨同長度的空心方管，2種長度組合的板型聲學超構材料的諧振頻率點均出現了少許紅移。以40 mm和50 mm這2種長度組合的聲學薄板為例，其透射曲線出現2個透射阻帶，阻帶峰值分別為2 025 Hz和1 640 Hz，與單獨的40 mm（2 070 Hz）和50 mm（1 665 Hz）聲學薄板相比，諧振頻率出現少許紅移。結合聲電類比分析其原因可能為相鄰的空心方管出現相互耦合作用，使得等效聲感增加，從而導致諧振頻率的降低。

圖4 2種不同長度組合聲學薄板透射曲線Fig.4 Transmission of acoustic thin plane with two different lengths

類似的，由40 mm和60 mm、40 mm和70 mm、50 mm和60 mm、50 mm和70 mm組合的聲學薄板對應的諧振頻率分別為2 020 Hz和1 375 Hz，2 005 Hz和1 185 Hz，1 630 Hz和1 370 Hz，1 630 Hz和1 185 Hz。另外，空心方管的長度越長，透射阻帶峰值的紅移越明顯，這主要是由于長度增加使得耦合作用增強所致。

因此，2種不同長度的空心方管組合的聲學薄板能夠實現雙頻帶的聲透射阻帶。

2.2 三頻帶并聯型聲學超構材料的透射性能

基于雙頻帶聲學薄板，設計了3種不同長度，即40，50 mm和60 mm的空心方管組合構建的聲學薄板（圖5）。其中，板長L1為100 mm，薄壁將每個腔體分割為2個獨立的OE－CE空心方管（即諧振腔），聲學薄板中共有18個諧振腔，中間6個諧振腔的長度為50 mm，左上及右下的6個諧振腔長度為40 mm，右上及左下的6個諧振腔長度為60 mm。

圖5 3種不同長度組合的聲學薄板結構Fig.5 Structure of acoustic thin plane with three different lengths

圖6為3種不同長度組合的聲學薄板的透射曲線，由圖可知，每一種聲學薄板的透射曲線均出現3個透射阻帶，阻帶峰值分別為1 380，1 620，2 020 Hz。從圖6還可以看出，在每個透射阻帶附近都伴隨相位突變，這進一步說明空氣柱在阻帶峰值附近發生諧振。另外，與單獨的40 mm（2 070 Hz），50 mm（1 665 Hz）和60 mm（1 395 Hz）聲學薄板相比，其峰位出現少許紅移，這是由于相鄰的空心方管出現相互耦合作用所致。

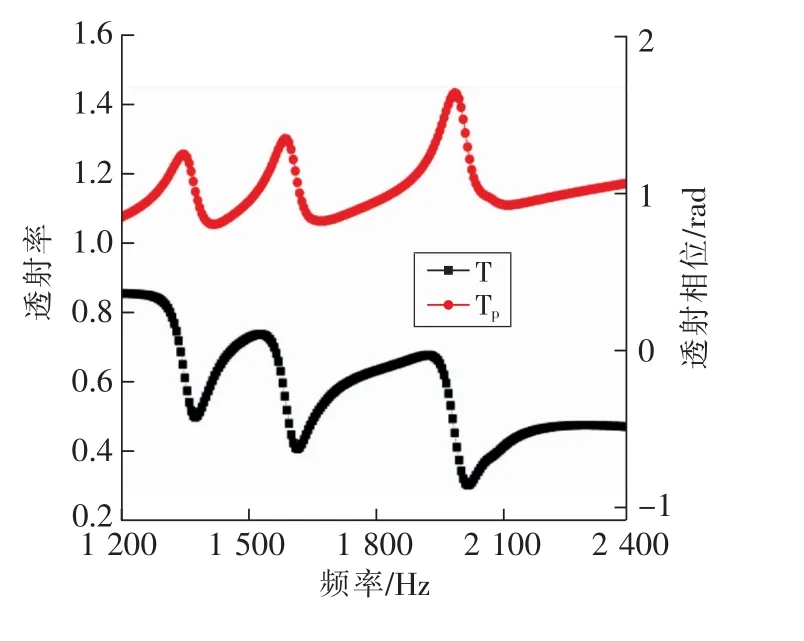
圖6 3種不同長度組合的聲學薄板透射曲線Fig.6 Transmission of acoustic thin plane with three different lengths

因此，3種不同長度的空心方管組合的聲學薄板能夠實現三頻帶的聲透射阻帶。

2.3 多頻帶并聯型聲學超構材料的透射性能

為研究多頻帶聲學薄板超材料，設計10種不同長度，即32，34，36，38，40，60，62，64，66 mm和68 mm的空心方管組合構建的聲學薄板，如圖7所示。

圖7 10種不同長度組合的聲學薄板結構Fig.7 Structure of acoustic thin plane with ten different lengths

圖8為多長度組合下的聲學薄板的透射曲線。由圖可知，低頻處出現1個寬的透射阻帶，高頻處出現5個窄的透射阻帶，這6個透射阻帶與單獨不同長度的空心方管對應的諧振頻率大致相符。從圖8還可以看出，在每個透射阻帶附近都伴隨相位突變，說明在每一個透射阻帶附近均發生了諧振。

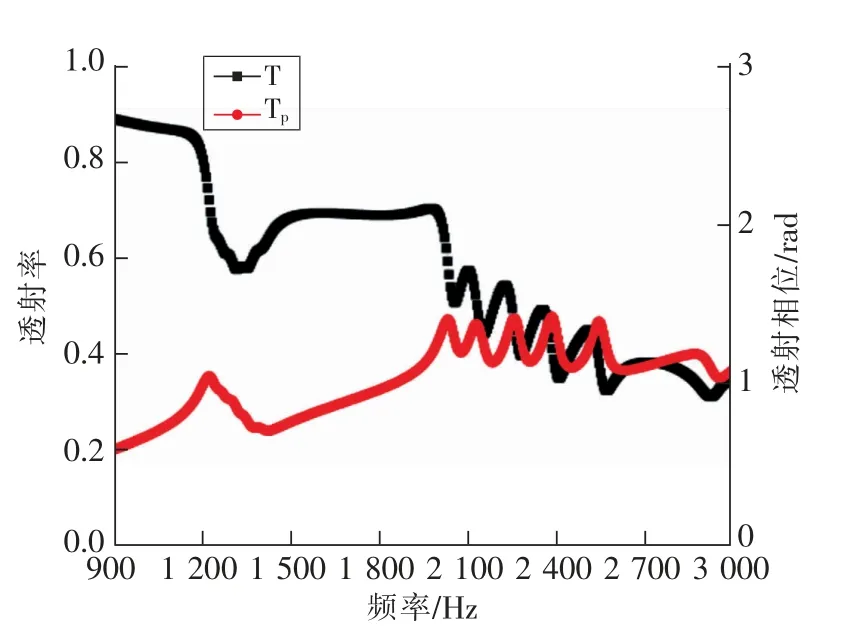
圖8 10種不同長度組合的聲學薄板透射曲線Fig.8 Transmission of acoustic thin plane with ten different lengths

進一步分析多長度組合下的聲學薄板透射曲線。在低頻處，透射阻帶的最低峰值較高；在高頻處，透射阻帶的最低峰值較低。其原因可能是：每種尺寸的諧振腔只有2個，不同尺寸的空心方管對聲波的吸收能力并不相同，且諧振腔在低頻處的吸聲能力弱，在高頻處的吸聲能力強，使得相同數目的空心方管在低頻處的透射阻帶幅值較小，導致透射阻帶的最低峰值較高。因此，在設計組合聲學薄板時需要增加較低諧振頻率處對應尺寸的空心方管數目。另外，從圖8還可以看出，間隔為2 mm的空心方管在高頻處出現獨立的透射阻帶。因此，在高頻處設計一定帶寬的透射阻帶時則需要縮小相鄰空心方管的長度梯度。

綜上，在設計多頻帶或寬頻帶的聲學超構材料板時，在較低頻率區域需要增加對應尺寸的空心方管數目，在較高頻率區域需要減小相鄰空心方管的長度梯度。

3 結論

1）對于嵌有不同長度的空心方管的聲學超構材料板：不同管長的空心方管的聲學薄板均能夠表現出透射阻帶和負等效質量密度特性。隨著方管長度的增加，透射阻帶出現紅移，且阻帶峰位升高。

2）透射阻帶的頻帶個數與不同長度的空心方管種類數目有關。由2種不同長度的空心方管組合的聲學薄板，在其對應的2個諧振頻率附近均表現出明顯的聲透射阻帶。其中，空心方管的長度越長，透射阻帶的紅移現象越明顯。而由3種不同長度的空心方管組合的聲學薄板則能夠在對應的3個頻帶附近實現聲透射阻帶。

3）對于實現寬頻帶聲學薄板：在較低頻率區域需要增加對應尺寸的空心方管數目，而在較高頻率區域則需要減小相鄰空心方管的長度梯度。