一類分數金融資產價格過程的近似解及其期權定價

王繼霞,肖曉芳

(河南師范大學 數學與信息科學學院,河南 新鄉 453007)

在金融一體化的背景下,描述各金融資產價格之間的長記憶性是金融時間序列分析中的一個重要研究內容.關于時間序列長記憶性的研究最早可以追溯到1951年,HURST[1]基于800多年的數據對尼羅河的長期水流特征進行了研究,發現尼羅河的水位特征具有自相似性和長記憶性.此后,人們在股票、利率、匯率等許多金融時間數據中也發現了這種現象,并對這種現象進行了更深入的研究.比如BAILLIE[2]討論了對長記憶波動過程及其在金融中的應用;BERAN[3]和GRANGER等[4]研究了一類平穩過程的長期相關性等.RATTIKAN[5]研究了分數過程驅動的分數Hull-White模型,代替了由標準布朗運動驅動的傳統Hull-White利率模型.此外,RATTIKAN[6]將幾何布朗運動驅動的Black-Scholes模型改進為分數Black-Scholes模型,并驗證了分數Black-Scholes模型可以更好地擬合IBM歷史股票數據.

近年來,關于我國金融市場長相依性特征的研究也很多,比如,李志生等[7]根據有效市場理論及分形市場假說,應用序列相關檢驗及R/S檢驗法分析研究出我國股票市場具有顯明的長相依性.苑瑩等[8]運用一系列檢驗方法研究了我國的股市收益率和成交量的長相依性特征.肖煒麟等[9]對金融市場數據進行了實證研究,發現金融資產價格具有長相依性.張躍軍等[10]研究了原油價格波動,證明原油市場波動存在結構性變化和長記憶特征.長記憶性側重探究價格序列本身在較遠時間間隔時是否仍具有持續依賴關系.將時間序列長記憶性特征分析運用于金融環境,可以準確把握金融市場的運行規律并構造符合實際的精確預測模型.

由于金融環境的不確定性,使得金融資產的價格過程呈現出長記憶特征,這意味著經典的布朗運動在某種程度上不能很好地描述資產價格過程,很多已有的研究表明利用分數布朗運動能有效捕捉資產價格長相依這一現象.然而,由分數布朗運動驅動的金融模型卻在金融市場中存在套利機會.為解決這一問題,本文針對金融環境中存在的長記憶現象,構建具有半鞅性質的分數高斯過程驅動的金融資產價格模型,并得到模型解的閉式表達式及其期權定價公式.本文所構建的模型在金融市場中不存在套利機會,這給人們研究期權定價問題帶來了方便.

1 金融資產價格模型與近似模型構建

設{Xt,t≥0}為金融資產的價格過程,滿足由分數布朗運動驅動的如下隨機微分方程,

(1)

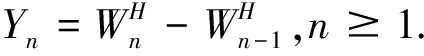
本文所研究的模型是很多金融中著名模型的推廣,如下面的注釋.

注1(a)當函數γ(t)=0時,模型(1)為金融中著名的分數Hull-White模型.

(b)當函數α(t)=0且σ(t)=0時,模型(1)為分數Black-Derman-Toy模型.

(c)當函數α(t)=α,β(t)=β,σ(t)=σ,且γ(t)=0時,其中α,β,σ為常數,則模型(1)為金融中的分數Vasicek模型.

(d)當函數α(t)=α,β(t)=β,γ(t)=γ,且σ(t)=0時,模型(1)為分數Dothan模型.

因此模型(1)是一類分數金融資產價格過程[11].

由文獻[12]知,分數布朗運動可以表示為:

(2)

其中Γ(·)是伽馬函數,(Wt)t≥0是標準布朗運動,且

(3)

(4)

(5)

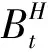
下面將給出模型(5)的由半鞅驅動的近似模型,并討論該模型的解.對?ε>0,定義

(6)

其中{Wt,t≥0}是標準布朗運動.注意到下面的積分

因此

(7)

令

(8)

則式(7)可表示成

(9)

(10)

這里‖·‖表示L2(Ω)中的范數,C(H)為僅依賴于H的常數.由式(10)可得,當ε→0時,

(11)

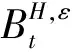
下面構建模型(5)的近似模型,對?ε>0,考慮如下隨機微分方程:

(12)

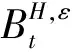
下面的定理1給出了模型(12)中解的表達式.

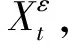
(13)

其中

(14)

證明由式(9)可得,

(15)

把式(15)代入式(12)可得:

(16)

顯然模型(16)是由標準布朗運動{Wt,t≥0}驅動的線性隨機微分方程,且是如下形式的線性隨機微分方程:

dX(t)=(m(t)+n(t)X(t))dt+(p(t)+q(t)X(t))dWt.

(17)

已知m(t),n(t),p(t),q(t)是t的連續函數,則式(17)的解是唯一存在的.

由文獻[17]可知,式(17)的解的形式如下:

(18)

其中

(19)

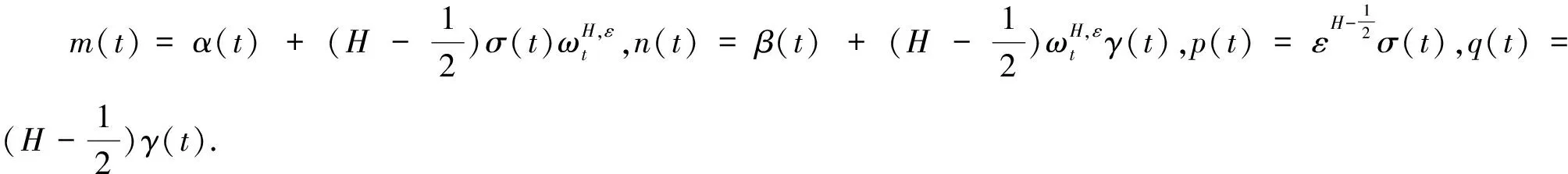
(20)

其中

(21)

證畢.

2 模擬研究

其中N是區間[0,t]上的分割區間個數,由于{Wt,t≥0}是標準布朗運動,故有

其中{ξk,k=0,1,2,…,N-1}是獨立同分布的標準正態隨機變量.

模擬步驟如下:

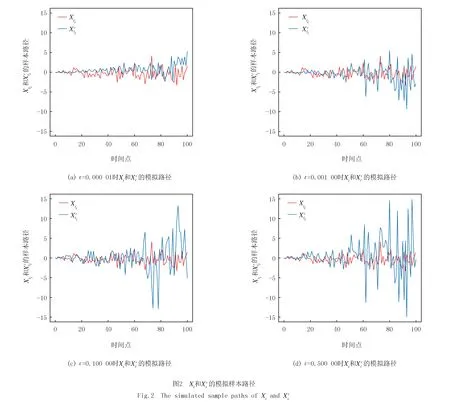
(i)參數設定:設定T=1,分別設定H=0.125,0.375,0.625,0.875,ε=0.062 5,0.125 0,0.250 0,0.500 0.

(ii)Ni為區間[0,ti]上分割區間數,i=1,2,…,500,生成標準正態隨機數g1,g2,…,gNi-1,計算

(22)

(iv)模擬上述程序20次.

(23)

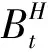
(24)

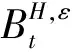
(25)

此外,由定理1可得模型(24)的解為:

(26)

3 基于近似模型的幾何平均亞式期權定價

(27)

由半鞅驅動的金融模型在金融市場環境中是無套利的,下面研究模型(27)的期權定價問題.設K為敲定價格,T是到期日,則看漲期權的支付為(AT-K)+,看跌期權的支付為(K-AT)+.這里AT表示在執行時間[0,T]上金融資產的平均價格,其計算公式為:

(28)

假設無風險利率為常數r,市場無摩擦,期權在到期日才能執行,則幾何平均亞式看漲期權和看跌期權的定價公式分別為:

C(K,T)=e-rTE[(AT-K)+].

(29)

和

P(K,T)=e-rTE[(K-AT)+].

(30)

下面的定理給出了期權定價公式的表達式.

(31)

和

(32)

證明由式(15)知,模型(27)可以寫為:

(33)

所以模型(27)在風險中性測度下的解為:

(34)

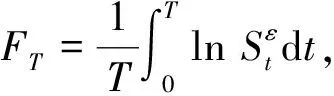
(35)

(36)

(37)

(38)