不同排列小間距雙方柱渦激振動數值模擬研究

鄔益東 李海泉 王曉欣 史力 吳莘馨

摘要 為研究不同排列下小間距雙方柱渦激振動特性及其振動機理，在雷諾數為100時，對間距比為2、質量比為3的串列、錯列和并列排列雙方柱渦激振動進行數值模擬研究，分析了雙柱在折合流速Ur=1～30下的響應振幅及頻率特性，并得到振動柱體的升阻力系數，以了解其氣動力系數的變化情況，探討了不同排列下雙柱尾流結構的變化情況。結果表明：串列及錯列排列中，下游柱渦激振動振幅遠大于單柱，上游柱振動受到抑制（θ=60°的雙方柱排列情況除外）。并列排列中，雙柱振動曲線幾乎一致，其渦激振動振幅比單柱稍大。各排列雙柱均發生尾流馳振現象，使其在Ur超出共振區時仍保持較高的振幅。不同排列的的雙柱阻力系數CD（θ=30°的雙柱排列下游柱除外）均在共振區內突增，在共振區外保持不變。在共振區內，雙柱CLrms隨Ur的變化情況與A*的大小有關；在其余Ur范圍內，雙柱CLrms基本不變。串列雙柱存在3種尾流模式，θ=30°雙柱排列的尾流模式與串列雙柱相似，但在超出共振區時，其尾流呈現無序狀態。在θ=60°，90°雙柱排列中，當Ur較大時，雙柱尾渦結構呈現混亂的狀態；當Ur較高時，柱體各自獨立脫落旋渦。

關鍵詞 渦激振動; 雙方柱; 串列; 錯列; 并列

引 言

流致振動在許多工程應用中是個重要的問題，其中均勻流中的圓柱或方柱是流致振動的研究熱點之一。已有許多學者對圓柱［1?6］以及單個方柱［7?8］的渦激振動進行了系統的研究，獲得了結構發生共振的條件，并用于指導工程設計。對于雙方柱渦激振動，由于影響因素眾多，其振動現象及機理的研究較為有限。

流體流經柱體后尾流的形式及其變化會顯著地影響結構振動特性，針對固定雙方柱繞流的研究已比較成熟，Sakamoto等［9］對不同柱間距（L/D=2.5～41，其中L為柱心的來流方向間距，D為方柱邊長）的串列雙方柱進行了研究，根據其斯特勞哈爾數St的分布將串列雙方柱的柱間流態分成三類。第一類為L/D<4時，此時上游柱的旋渦被壓制；第二類為428時，此時雙柱旋渦脫落不再同步，雙柱之間幾乎無影響。Sohankar［10］采用數值模擬的方法研究串列雙方柱繞流的流場特性，將Sakamoto等［9］的前兩類柱間流態進一步細分成單一鈍體流態、剪切層再附流態及耦合渦脫流態三類。對于并列雙方柱繞流，Alam等［11］根據其尾流及旋渦脫落情況將并列雙方柱（T/D=1.02～6， T為柱心的橫向間距）的尾渦結構分成單一鈍體流態、雙頻率流態、耦合渦脫流態及過渡流態四種。Alam等［12］又對錯列排列的雙方柱進行了研究，將雙方柱排列的繞流研究補充完整。橫向間距或來流方向間距較小的錯列雙方柱的尾流結構分別與并列和串列雙方柱排列一致。其他錯列排列情況下雙柱的尾流結構與并列排列中的雙頻率流態或耦合渦脫流態相似，僅在St數的大小及間隙流的偏轉方向上有所區別。

相比固定柱，對于彈性支承雙方柱的流致振動研究則十分有限，且大多數研究集中在數值模擬方面。Bhatt等 ［13］研究串列排列下固定方柱對下游方柱振動的影響，發現當柱間距較小時（L/D=2），下游柱渦激振動發生在較大的流速下，其振幅大小不變；當柱間距較大時（L/D=6），下游柱的渦致振動振幅增大。Han等［14］和Nepali等［15］在Re=40～200時，對上游方柱固定、下游方柱具有雙自由度及雙方柱均具有雙自由度的兩種情況進行了數值模擬，在串列雙方柱柱間距為5D時，研究了雷諾數對柱體振動特性及流場結構的影響。杜曉慶等［16?18］對Re=150下的串列雙方柱進行了數值模擬，研究了柱間距（L/D=2，4）、質量比（m*=3，10，20）對雙柱振動及流場特性的影響。Guan等［19?21］在Re=200， m*=10時，對剛性連接的并列雙方柱進行數值模擬研究，發現了并列雙柱系統的四種振動模式。

雙方柱渦激振動的問題仍有許多方面尚需進一步研究，尤其是錯列雙方柱情況。雙柱間距較小時，其尾渦相互之間的影響較大［11］，綜合考慮數值建模的可行性，本文在柱間距為2D的情況下，對橫向自由振動的不同排列雙方柱進行數模擬研究，得到不同折合流速下雙方柱的振動響應，同時研究不同排列下雙方柱氣動力特性及流場結構的變化。

1 數值計算模型

1.1 基本控制方程及柱體運動方程

計算流體力學的基本控制方程為：能量方程、運動方程及連續性方程。本文不考慮流體溫度的變化，流體視為不可壓縮的黏性流體，因此主要的控制方程為連續性方程及運動方程。

連續性方程：

式中 ui為流體的速度分量。

運動方程（N?S方程）：

式中 ρ為流體的密度，視為常數；p為流體壓強；μ為流體的動力黏度系數。

雙方柱的計算模型如圖1所示。其中，柱體邊長為D，柱心間距P=2D，柱心連線與x軸方向的夾角為θ，U為來流速度，與x軸同方向。下標1代表為位于原點O左（下）方的柱體1，下標2代表為位于原點O右（上）方的柱體2。雙柱僅在y方向上自由振動，柱體的運動方程為：

式中 y為柱體的位移；c為柱體結構阻尼；k為彈簧剛度；m為柱體單位長度質量；FL（t）=0.5ρU2DCL為柱體受到的y方向流體力分量，其中，CL為升力系數。

為方便觀測不同排列下雙柱結構與流體之間的相互作用，選取m*=3，c=0作為柱體的結構參數，以保證柱體的振動幅度足夠大。

1.2 邊界條件及網格劃分

基于數值計算軟件Fluent，對雙方柱的渦激振動進行數值模擬，計算域的設置如圖2所示。來流為均勻平行來流，流速為U，雷諾數Re=100。在該雷諾數下，認為三維效應影響很小［22?23］，且來流為層流。同時，低雷諾數下觀測到的渦激振動（VIV）行為也能較好地預測高雷諾數下的VIV行為［24］。入口邊界采用速度入口邊界，距柱體中心距離為25D。出口采用壓力出口邊界條件，距柱體中心50D。上下邊界距離為40D，采用對稱邊界條件，柱體表面設為無滑移壁面。

采用嵌套網格技術進行數值模擬，該技術能克服動網格易出現負體積網格的問題，可以適應復雜的結構運動，能在結構運動的過程中保持較好的網格質量。文獻［25?26］表明，嵌套網格技術在工程運用的數值模擬中能提供較高的準確度。計算模型的網格如圖3所示，背景網格和部件網格均采用結構化網格。求解器采用基于壓力的壓力耦合求解器，算法為Couple算法。考慮計算結果的精度，采用二階迎風格式進行空間離散、一階隱式格式進行時間離散。柱體運動方程的求解采用四階龍格?庫塔法并通過UDF實現。

1.3 網格參數

以Re=100，θ=0°的串列雙方柱靜態繞流為研究算例，研究網格密度、計算時間步長對數值計算結果的影響，不同參數下固定串列雙方柱繞流的計算結果如表1所示。其中CLrms為升力系數均方根（本文中的均方根均為數據除去直流信號（即減去平均值）后的取值，下文中yrms也如此），CD為平均阻力系數。考慮計算時間成本和計算結果的準確度，選取網格數為74294的網格模型，時間步長取0.01。

1.4 數值計算模型的驗證

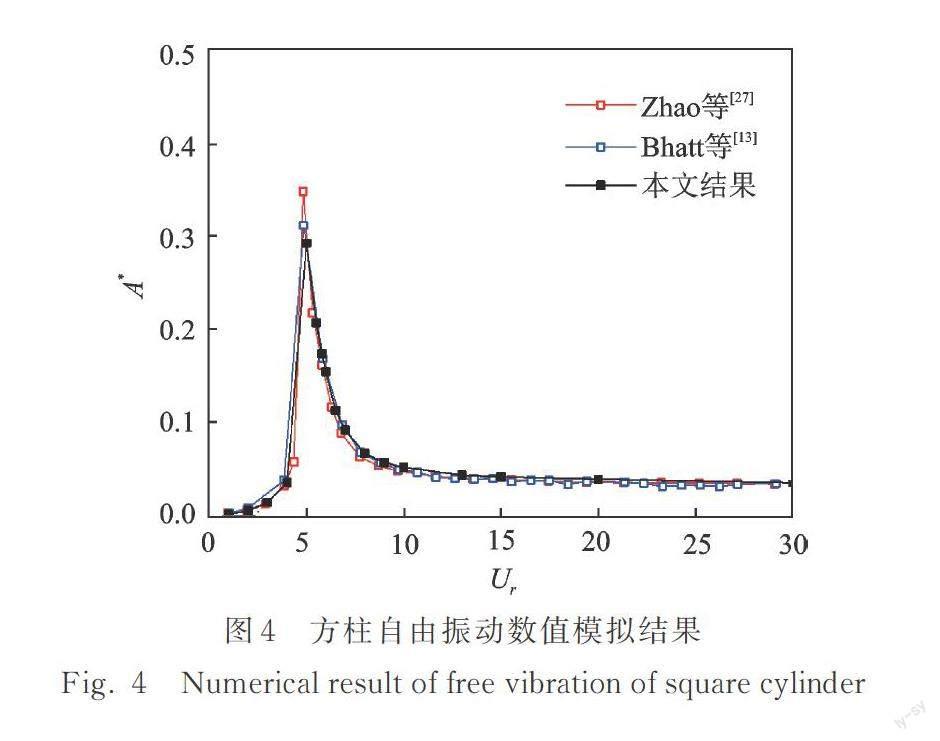
選取Re=100，m*=3，c=0的單方柱為算例，其靜態繞流計算結果與文獻的比較如表2所示。進行方柱單自由度自由振動的模擬，通過改變方柱的自振頻率從而改變折合流速，得到方柱的渦激振動響應曲線，如圖4所示。圖4中，折合流速Ur及無量綱位移A*可由下式計算：

式中 fn為柱體的自振頻率；yrms為柱體位移y的均方根。

由表2及圖4可以發現，固定柱繞流各項參數和振動響應的振幅曲線均與其他文獻的結果十分接近，驗證了數值計算模型的準確性。

2 計算結果與分析

雙方柱渦激振動的數值計算在Re=100，m*=3，ζ=0，P/D=2的條件下展開，考慮四種不同位置的雙方柱排列（θ=0°（串列），30°，60°，90°（并列）），計算的折合流速范圍為1～30，每個算例都經過足夠長時間的計算以保證柱體達到穩態響應。

2.1 振動響應特性

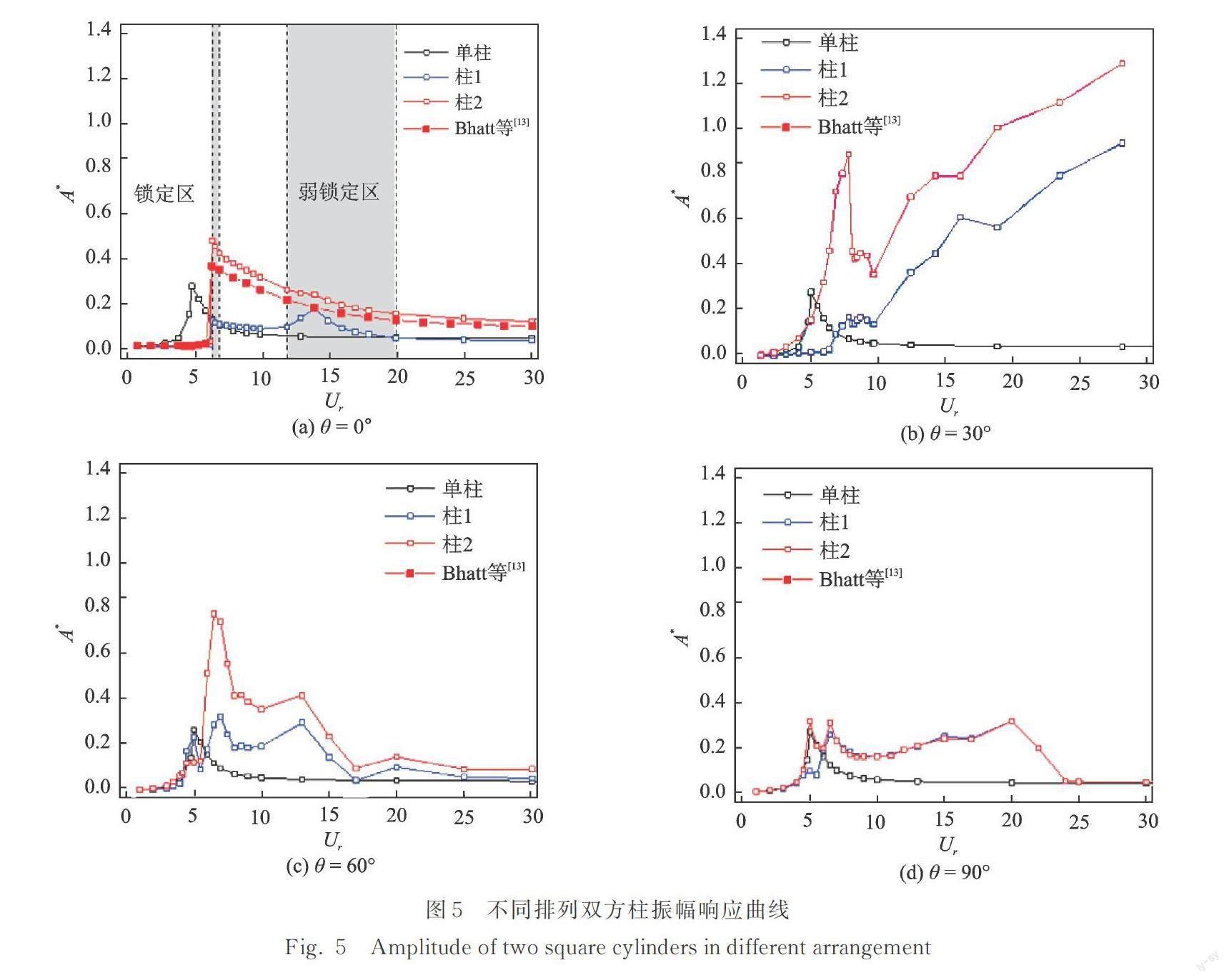
不同排列雙方柱的A*隨Ur的變化情況如圖5所示，單方柱的計算結果也在圖中給出以進行比較。當雙方柱呈串列（θ=0°）排列時，與單方柱相比，初始分支時，雙柱的振幅被抑制；下端分支時，上游柱（柱1）渦激振動振幅被抑制，下游柱（柱2）則相反。下游柱振幅曲線僅在Ur=6.5出現一個峰值，該折合流速比單柱共振發生時的折合流速（Ur=5）略大。上游柱在Ur=6.5，14處出現兩個峰值，且第二個峰值比第一個峰值稍大。當Ur >20時，上游柱的振幅與單柱接近，而下游柱仍保持較大的振幅。圖5中給出相同條件下，處于固定上游柱尾流中的下游柱的振幅響應［13］。對比可以得出結論，上游柱的振動增大了尾流作用于下游柱的強度，使得下游柱的振幅增大。當θ=30°時，下游柱初始分支的振幅急劇增大，其峰值約為單柱的3倍多，對應的折合流速Ur=8。當Ur>10時，下游柱的振幅隨著流速的增大迅速增大，出現類似于馳振的振動現象。該現象在串列雙圓柱的渦激振動研究中也被觀測到［30］，其被稱為尾流馳振。上游柱的振動響應與下游柱類似，但上游柱Ur=8處的峰值較小，且其整體振幅均比下游柱小。當θ=60°時，雙柱振幅曲線均在Ur=6.5，13處出現兩個峰值，上游柱的兩個峰值一樣大，下游柱振幅曲線的第一個峰值約為第二個峰值的2倍。當θ=90°時，雙柱在Ur=5處振幅有所不同，上游柱出現較大的振幅，而下游柱振幅偏小。除此之外，雙柱振幅曲線基本一致，均在Ur=6.5，20處出現峰值，且兩個峰值大小相差不大。下文將結合流場情況對對稱的并列雙柱結構出現不同振幅的情況進行解釋。

圖6為不同Ur下串列雙方柱振動位移的無量綱功率譜密度（PSD）。對比雙柱的功率譜密度，可以發現雙柱振動頻率基本一致。當Ur<12或Ur>20時，雙柱均以單一的頻率振動；當12

圖8為不同Ur下其他排列雙方柱振動位移的無量綱PSD。由于同一排列的兩個方柱振動頻率分布類似，因此圖中只給出了柱1振動位移的PSD。對于θ=30°的雙方柱排列情況，在Ur<10的范圍內，柱體主要的振動頻率不變，這是由于旋渦脫落導致的振動頻率。當Ur>10時，柱體發生與串列排列106時，柱體發生“弱鎖定”現象，但振動頻率仍保持較寬的頻率帶。對于θ=90°的雙方柱排列情況，柱體在Ur=5發生旋渦脫落共振，呈現單一振動頻率。柱體在Ur>24時，以單一的旋渦脫落頻率振動。除了上述范圍外，柱體振動頻率呈現極其寬闊的頻率帶，頻率大致分布在約為0.15的旋渦脫落頻率及fv/fn=0.8的“弱鎖定”頻率周圍。由上可以總結得到，雙方柱振動頻率主要由旋渦脫落頻率及“弱鎖定”頻率組成。在折合流速較低時，旋渦脫落頻率占主導，且不出現“弱鎖定”頻率；當折合流速較大時，除個別情況外（串列排列的下游柱），“弱鎖定”頻率占主導；當折合流速超出一定范圍時，旋渦脫落頻率又取得主導地位。對比圖8的各子圖可以發現，隨著θ的增大，振動頻率分布的頻帶越來越寬。這與雙柱橫向間距增大而帶來的無序間隙流密切相關，文章后面會給出相應的流場結構進行解釋。

2.2 氣動力特性

圖9給出了不同排列雙方柱CD隨Ur的變化情況。對于串列雙方柱排列情況（見圖9（a）），當Ur<5.5時，雙柱CD基本保持不變，下游柱CD2由于上游柱尾流區的負壓作用而出現負值［9］。當共振發生時（Ur=6.5），CD1突增，之后隨著Ur的增大逐漸增大，超出共振區后又緩慢減小至定值。CD2在Ur=6.5時突增至最大值，且其值由負數轉為正數，之后逐漸減小。由于柱2相對于柱1較大的振幅，使柱1失去“遮擋”作用，柱2離開柱1尾流的負壓區，直接暴露在來流中，CD2變成正值。柱2與柱1的相對位移決定了柱2離開負壓區的前表面面積，相對位移越大，柱2在負壓區外的前表面面積越大，CD2越大，因此CD2隨Ur的變化趨勢與A*2一致。圖9（b）給出了θ=30°時雙方柱CD情況，CD1的變化趨勢與θ=0°時的情況類似。當Ur<5，CD2比CD1稍大；在共振區（5≤Ur≤8）內，CD2突增，其值一直保持在較大值；超出共振范圍時，CD2呈現斷崖式下跌，之后隨著Ur增大漸漸減小。對于θ=60°的雙方柱排列情況（見圖9（c）），CD1曲線除了在共振區出現一個峰值外，在其他Ur處均接近于定值，該值比其在θ=0°，30°時要大。CD2未達到共振區時接近于1.5，在共振區內，CD2先減小至最小值，而后迅速增大至最大值又急速減小。在Ur超出共振區時，CD2沒有太大的變化。當雙柱處于并列排列時，雙柱CD曲線（見圖9（d））十分相似，僅在共振區的發展有所不同。共振區外，雙柱CD均保持在一定值附近；共振區內，CD1先減小后增大，CD2則先增大后減小。

圖10給出了不同排列雙方柱CLrms隨Ur的變化情況，將其與圖5中A*隨Ur的變化情況作對比，可以發現A*與CLrms之間的關系。不同排列下雙方柱A*受渦激振動和尾流馳振的影響。可以發現，渦激振動發生時，A*與CLrms成正比關系，圖10中各CLrms曲線的峰值都能在圖5中一致的Ur處發現相應的振幅曲線峰值。尾流馳振發生時，其CLrms有一定程度的增大，但其大小與A*無關。θ=30°的雙方柱排列中，當Ur>10時，雖然A*隨Ur的增大而增大，但其CLrms基本保持不變。并列排列中，雙方柱A*曲線在10

2.3 流場結構特征

圖11為串列排列雙方柱的三種尾流結構。當Ur≤6.3時，雙柱尾流結構如圖11（a）所示，由于雙柱振幅均較小，其尾流較穩定，脫落的旋渦渦度較小，下游柱背風面出現正反旋渦共存的兩條平行渦街，其渦街在下游距柱體較遠處轉變為“2S”模式。當6.3≤Ur≤7.5，此時雙柱處于旋渦脫落共振狀態，振幅較大，尾流結構如圖11（b）所示。下游柱由于大幅度的振動，周期性地交替脫落強度較大的正反旋渦，且正反旋渦橫向間距較大。旋渦在遠離柱體時，強度逐漸減小，正反旋渦之間的影響也減小，同向旋渦漸漸連成一片，形成兩條平行的渦街。當Ur≥7.5時，雙柱尾流呈現“2S”模式，如圖11（c）所示。由于下游柱振幅的降低，脫落的正反旋渦橫向間距減小，其橫向間距不足以形成兩條平行渦街，因此呈現“2S”模式。

θ=30°的雙方柱排列尾流結構如圖12所示。當Ur≤6.5或8.3≤Ur≤10時，雙柱尾流結構如圖12（a）所示，其旋渦形狀類似圖11（c）的旋渦，但由于其正向旋渦是雙柱分離的剪切層融合形成，比僅由下游柱剪切層形成的反向旋渦規模要大。由于雙柱橫向間距不為零，下游柱對上游柱分離剪切層的干擾關于x軸不對稱，因此當Ur≤6.5時，下游柱背風面并不能像圖11（a）那樣形成兩條平行渦街。當6.510時，雙柱發生尾流馳振，柱體的旋渦結構及其復雜，這是由于雙柱排列位置及下游柱過大的振動幅度導致的。當雙柱間距較小時，上游柱脫落的旋渦受到下游柱的干擾，如圖12（c）所示；當雙柱間距較大時，上游柱脫落的旋渦受到下游柱的影響極小，如圖12（d）所示。伴隨著雙柱間距的變化，其尾渦結構一直在這兩種狀態間逐漸變化，因此形成極其混亂的尾流結構。

圖13為θ=60°的雙方柱排列尾流結構。當Ur≤4.2及7.5≤Ur≤13時，此時雙柱間的間隙流極不穩定，偏轉方向在雙柱之間無規律變化，導致雙柱后無序的旋渦脫落情況，如圖13（a）所示。當4.2

圖14展示了并列雙方柱的尾流結構，其與θ=60°的雙方柱排列類似。當Ur≤4.5及6

3 結 論

本文在Re=100，m*=3，ζ=0時，對間距比P/D=2的雙方柱排列在Ur=1～30下的渦激振動進行了數值模擬研究，考慮了串列、并列、錯列的雙柱排列情況，得到了以下結論：

（1） 對于串列及錯列的雙方柱排列情況，下游柱渦激振動振幅增大，上游柱渦激振動振幅受到抑制。對于并列排列情況，雙方柱振動曲線幾乎一致，其渦激振動最大振幅比單柱稍大。對于θ=60°的雙柱排列情況，當Ur>10時，尾流馳振發生，振幅隨著Ur的增大而增大。而在雙柱其他排列情況中，尾流馳振僅在10

（2） 當尾流馳振發生時，雙柱存在“弱鎖定”振動頻率，由旋渦脫落導致的振動頻率則在各Ur下均存在。對于θ=0°，30°的雙柱排列情況，雙柱振動頻率集中在單一的頻率上；當θ=60°，90°時，振動頻率分散在較寬的頻率帶。

（3）除θ=30°排列外，其余排列的雙柱CD均在共振區內突增，在共振區外保持不變。對于θ=30°的雙柱排列，其下游柱CD在Ur超出共振區時隨著Ur的增大逐漸減小，而上游柱CD在共振區外也保持不變。在共振區內，雙柱CLrms隨Ur的變化情況與A*隨Ur的變化趨勢一致；當尾流馳振發生時，其CLrms有一定程度的增大，但其大小與A*無關。在其余Ur范圍內，雙柱CLrms基本不變。

（4）串列雙柱存在3種尾流模式，這些模式由平行渦街模式及“2S”模式組合構成。θ=30°雙柱排列的尾流模式與串列雙柱相似，但在超出共振區時，其尾流呈現無序狀態。在θ=60°，90°雙柱排列中，當Ur較大時，雙柱尾渦結構呈現混亂的狀態；當Ur較高時，柱體各自獨立脫落旋渦。

參考文獻

1Williamson C H K， Govardhan R. Vortex induced vibrations［J］. Annual Review of Fluid Mechanics， 2004，36：413-455.

2Bearman P W. Circular cylinder wakes and vortex-induced vibrations［J］. Journal of Fluids and Structures， 2011， 27（5-6）：648-658.

3Sarpkaya T. A critical review of the intrinsic nature of vortex-induced vibrations［J］. Journal of Fluids and Structures， 2004， 19（4）：389-447.

4Gabbai R D， Benaroya H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders［J］. Journal of Sound and Vibration， 2005， 282（3-5）：575-616.

5Alam M M， Kim S. Free vibration of two identical circular cylinders in staggered arrangement［J］. Fluid Dynamics Research， 2009， 41（3）：035507.

6Qin B， Alam M M， Zhou Y. Free vibrations of two tandem elastically mounted cylinders in crossflow［J］. Journal of Fluid Mechanics， 2019， 861：349-381.

7Obasaju E D， Ermshaus R， Naudascher E. Vortex-induced streamwise oscillations of a square-section cylinder in a uniform stream［J］. Journal of Fluid Mechanics， 1990， 213：171-189.

8Nemes A， Zhao J， LoJacono D， et al. The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack［J］. Journal of Fluid Mechanics， 2012， 710：102-130.

9Sakamoto H， Hainu H， Obata Y. Fluctuating forces acting on two square prisms in a tandem arrangement［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1987， 26（1）：85-103.

10Sohankar A. A numerical investigation of the flow over a pair of identical square cylinders in a tandem arrangement［J］. International Journal for Numerical Methods in Fluids， 2012，70（10）：1244-1257.

11Alam M M， Zhou Y， Wang X W. The wake of two side-by-side square cylinders［J］. Journal of Fluid Mechanics， 2011， 669：432-471.

12Alam M M， Bai H， Zhou Y. The wake of two staggered square cylinders［J］. Journal of Fluid Mechanics， 2016， 801：475-507.

13Bhatt R， Alam M M. Vibrations of a square cylinder submerged in a wake［J］. Journal of Fluid Mechanics， 2018， 853：301-332.

14Han Zhaolong， Zhou Dai， Malla Anamika， et al. Wake-induced vibration interference between a fixed square cylinder and a 2-DOF downstream square cylinder at low Reynolds numbers［J］. Ocean Engineering， 2018， 164：698-711.

15Nepali Ramesh， Ping Huan， Han Zhaolong， et al. Two-degree-of-freedom vortex-induced vibrations of two square cylinders in tandem arrangement at low Reynolds numbers［J］. Journal of Fluids and Structures， 2020，97：102991.

16杜曉慶，邱濤，趙燕.低雷諾數下串列雙方柱尾流致渦激振動研究［J］.振動工程學報，2020，33（5）：985-993.

DU Xiaoqing， QIU Tao， ZHAO Yan. Numerical simulation of wake-induced vortex vibration on two tandem square cylinders［J］. Journal of Vibration Engineering， 2020，33（5）：985-993.

17杜曉慶，邱濤，鄭德乾，等.低雷諾數中等間距串列雙方柱渦激振動的數值模擬［J］.哈爾濱工業大學學報，2020，52（10）：94-101.

DU Xiaoqing， QIU Tao， ZHENG Deqian， et al. Numerical simulation on vortex-induced vibration of two tandem square cylinders with medium spacing at a low Reynolds number［J］. Journal of Harbin Institute of Technology， 2020，52（10）：94-101.

18杜曉慶，邱濤，趙燕.低雷諾數串列雙方柱流致振動質量比效應的數值研究［J］.力學學報，2019，51（6）：1740-1751.

Du Xiaoqing，Qiu Tao，Zhao Yan. Numerical investigation of mass ratio effect on flow-induced vibration of two tandem square cylinders at low reynolds number［J］. Chinese Journal of Theoretical and Applied Mechanics， 2019，51（6）：1740-1751.

19Guan M Z， Jaiman R K， Kang C W， et al. Freely vibrating two side-by-side square columns with combined translational motions［C］. ASME 2016 35th International Conference on Ocean， Offshore and Arctic Engineering， Busan， South Korea， 2016.

20Guan M Z， Jaiman R K. Flow-induced vibration of two side-by-side square cylinders with combined translational motions［J］. Journal of Fluids and Structures， 2017， 69：265-292.

21Guan M Z， Jaiman R K， Narendran K， et al. Fluid-structure interaction of combined and independent configurations of two side-by-side square cylinders at low Reynolds number［J］. International Journal of Heat and Fluid Flow， 2018， 72：214-232.

22Borazjani I， Sotiropoulos F. Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity?wake interference region［J］. Journal of Fluid Mechanics， 2009， 621：321-364.

23Papaioannou G V， Yue D K P， Triantafyllou M S， et al. Three-dimensionality effects in flow around two tandem cylinders［J］. Journal of Fluid Mechanics， 2006， 558：387-413.

24Bao Y， Huang C， Zhou D， et al. Two-degree-of-freedom flow-induced vibrations on isolated and tandem cylinders with varying natural frequency ratios［J］. Journal of Fluids and Structures， 2012， 35：50-75.

25Wang H， Ding L， Zhang L， et al. Control of two-degree-of-freedom vortex-induced vibrations of a circular cylinder using a pair of synthetic jets at low Reynolds number： influence of position angle and momentum coefficient［J］. International Journal of Heat & Fluid Flow， 2019， 80：108490.

26Zou Q， Ding L， Wang H， et al. Two-degree-of-freedom flow-induced vibration of a rotating circular cylinder［J］. Ocean Engineering， 2019， 191：106505.

27Zhao M， Cheng L， Zhou T. Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number［J］. Physics of Fluids， 2013， 25（2）：023603.

28Sahu A K， Chhabra R P， Eswaran V. Two-dimensional unsteady laminar flow of a power law fluid across a square cylinder［J］. Journal of Non-Newtonian Fluid Mechanics， 2009， 160（2-3）：157-167.

29Sharma A， Eswaran V. Heat and fluid flow across a square cylinder in the two-dimensional laminar flow regime［J］. Numerical Heat Transfer. Part A， Applications， 2004， 45（3）：247-269.

30Sun Q， Alam M M， Zhou Y. Fluid-structure coupling between two tandem elastic cylinders［J］. Procedia Engineering， 2015， 126：564-568.

Numerical simulation on vortex-induced vibration of two square cylinders with small spacing in different arrangement

WU Yi-dong 1 ?LI Hai-quan 2WANG Xiao-xin 1SHI Li 1 ?WU Xin-xin 1

1. Institute of Nuclear and New Energy Technology， Tsinghua University， Beijing 100084， China；

2. Huaneng Shangdong Shidao Bay Nuclear Power Co.， Ltd.， Weihai 264312， China

Abstract In order to investigate the vortex-induced vibration characteristics and vibration mechanism of two square cylinders with small spacing in different arrangements， numerical simulation on vortex-induced vibration of two square cylinders in tandem， parallel， staggered arrangement is carried out at Reynolds number Re=100 with the spacing ratio of 2 and the mass ratio of 3. The amplitude and frequency of vortex-induced vibration （VIV） response of two square cylinder at Ur=1-30 is studied and the lift and drag coefficient are obtained to understand the characteristic of the aerodynamic coefficient. The wake structures of two square cylinders in different arrangements are analyzed. The results show that the vibration amplitude of downstream cylinder in tandem，staggered arrangement is much larger than that of single square cylinder while the vibration of upstream cylinder is suppressed （except the case of θ=60°）. The amplitude curves of two cylinders in parallel arrangement are almost identical， with the vibration amplitude larger than that of single square cylinder. The wake galloping phenomenon of two cylinders is observed in all arrangement， which make the cylinders maintain a lager amplitude as Ur exceeds the resonance range. The CD of two cylinders in different arrangement abruptly increases in the resonance range and keeps constant beyond the resonance range （except the CD of downstream cylinder at θ=30°）. In the resonance Ur range， the variations of CLrms with Ur of two cylinders are related to the A* while that keeps constant beyond the resonance range. There are three wake mode of two square cylinders in tandem arrangement. The wake structure of cylinders at θ=30° is similar to that of cylinders in tandem， while it is in a state of chaos beyond the resonance range. As θ=60° and 90°， the shear layer of two square cylinders sheds disorderly at lower Ur while the vortex sheds individually from each cylinder at higher Ur.

Keywords vortex-induced vibration; two square cylinders; parallel arrangement; tandem arrangement; staggered arrangement