一種適用于非連通交通網絡的軍事輪式平臺機動路徑規劃方法研究
柳 玉 張莉麗 趙志軍
(中國人民解放軍91976部隊教研部 廣東 廣州 510430)
0 引 言
軍事輪式作戰平臺由海上路以后,機動是構成作戰基本過程的一種典型作戰行動。合適的機動路徑規劃是保證軍事輪式作戰平臺各項任務順利執行的前提。軍事輪式作戰平臺機動路徑規劃問題是指在給定起點和終點條件下,尋求一條通過交通路網機動時間最短的路徑。在當前的戰術訓練模擬系統或仿真實驗系統中,軍事輪式作戰平臺從搭載的兩棲艦船抵灘上路以后,機動到目的地有兩種路徑規劃方式:一是人在回路時,由操作員手工實時指定機動關鍵點,關鍵點不一定在交通路網上,可以在軍事輪式作戰平臺可行進的任一地理點,由系統自動采用插值算法將若干個首尾相接的直線段擬合成機動路線。此種方式能快速規劃好路徑,但是以能機動而不是最優為主要目的,很難兼顧到不同地形地貌對機動速度的影響,缺乏合理性。二是作戰實驗時,系統考慮地形地貌的影響,參考機動終點方向采用A*算法搜索計算中間機動點,最后給出完整機動路徑,經常出現耗時過長、結果路徑無法產生的問題[1]。
國內外專家學者對于路徑規劃算法進行了探索并取得了較多成果,常用的最優路徑算法主要包括Dijkstra算法[2]、Bellman-Ford算法[3]、Floyd-Warshall算法[4]、動態規劃算法[5]、SPFA算法[6]、A*[7]等,其中:Dijkstra算法與A*算法在計算時只需獲取當前點的后繼即可,理論上支持的機動交通路網圖可以無限大,適用性較好。其他四種算法針對連通圖可以計算當前點與其他所有點之間的最優路徑,尤其是Floyd-Warshall算法可以提前計算所有點之間的最優路徑,實現“一勞永逸”的效果。但當起點或終點不在交通路網圖上,即交通路網圖的數學模型是不連通的二分圖或者多分圖時,上述除A*算法以外全部失效。A*算法作為啟發式算法,可適用于連通或非連通的交通路網圖,但當交通路網區域過大時,搜索路徑會變長,導致大量無用節點產生,算法效率會急劇下降,容易陷入局部最優的凸頂錯誤[8-9]。
軍事輪式作戰平臺的工作環境決定了其上路點、機動目的地不可能直接處于交通路網附近,且敵縱深梯次配置的防御工事會生成出一個較大地理區域的交通網絡圖。針對上述需求,探索研究一種適用于非連通交通網絡的軍事輪式平臺機動路徑規劃方法不僅有助于提高戰術訓練模擬或仿真實驗系統的準確性、合理性及效率,還能為軍事輪式平臺選擇機動路線提供優選方案。近年來基于Geohash[10-12]算法快速尋找最優附近點為解決這一問題開辟了一條切實可行的道路。在考慮作戰環境對軍事輪式平臺機動性能影響情況下,可實現將非連通的起點或終點按照耗時最少的路徑連接到原有連通的交通路網,從而將非連通交通網絡中的機動路徑規劃問題轉換為求單起點、單終點的有向無環圖中的最優路徑問題。
1 路徑規劃問題分析與數學描述
1.1 問題分析
登陸場地域的坡度、地質、植被、水系、障礙等會對軍事輪式平臺機動性能產生影響。軍事輪式平臺通過某個區域除必須付出一定的時間代價外,還要面臨來自敵火力打擊的危險,因此,機動路線的選擇一般原則是從抵灘上路點能夠快速機動到目的地[13]。由于抵灘上路點和作為機動目的地的敵工事目標或指揮節點一般遠離交通路網,所以路徑規劃首先要使軍事輪式平臺能夠快速從抵灘點機動到交通路網,匯入交通路網的點稱之為上路點;其次,當軍事輪式平臺從上路點進入交通路網之后,按耗時最少的路徑行進;最后選擇在能最快到達目的地的位置點駛下道路,直接機動到目的地,駛下道路的點稱之為下路點。因此,通過尋找起點到上路點,終點到下路點的最短路徑,可以將起點和終點連接至已有交通路網,從而將非連通的路徑規劃問題轉化為單起點、單終點的連通路網的最短路徑問題。
1.2 交通路網圖的最優路徑
軍事地形圖采用矢量格式,由按照地圖要素分類的一系列圖層組成。交通路網圖層屬于其中的一個,主要由點、線構成。經過抽取公共點,合并重復邊,加入起點和終點以及起點到上路點的路徑、終點到下路點的路徑以后,可建立一個標準的有向無環圖G=(V,E,D,W)模型(Directed Acyclic Graph,DAG),其中,V是節點集{v0,v1,v2,…,vn};E是連接節點vi、vj的邊集{eij};D是邊eij的長度集{dij},n是節點數量。考慮地形地貌及道路的級別對軍事輪式平臺機動性能影響,給邊eij賦權值wij,表示軍事輪式平臺在兩個節點vi,vj之間的機動時間,W是權值wij的集合。針對矢量地形圖,此拓撲圖構造過程具有速度快、無需預處理、對地域大小不限制等顯著特點,且在理論上可證存在一條耗時最少路徑。
1.3 機動路徑規劃問題的數學描述
給定一個連通的交通路網圖G、起點S、終點T,一定存在至少一條從S到T耗時最少的路徑,設計軍事輪式作戰平臺通過這條路徑的最短時間模型:
f*(PST)=min{f(PST)}
式中:PST是指由S到T的一條通路,f(PST)指機動平臺在通路PST上耗費的時間。
2 圖層預處理與算法設計
交通路網圖層主要由表示道路交匯處的點和表示道路的線構成。軍事輪式平臺從起點到最近道路的路徑在數學意義上可抽象為點到線的最短歐氏距離,但在矢量軍事地形圖中情況復雜,原因在于軍事地形圖中,道路是以線要素來表示的,而線是用一系列坐標點來表示的,一條道路可以看成是一個有限坐標點的集合。一般來說,道路越平坦,表示該道路的坐標點越少;道路越曲折,表示該道路的坐標點越多。因此,尋找軍事輪式平臺從起點到最近道路的最短路徑可定義為尋找一點到數個有限點集中距離最近的點的過程。尋找下路點過程相同,不另作論述。
軍事輪式平臺從抵灘位置S到縱深要害目標T的最優路徑PST可以分解為:
(1) 尋找S到道路耗時最短的上路點u。
(2) 機動目的地T到道路的耗時最短的下路點v。
(3) 交通路網G中從上路點u到下路點v耗時最短的路徑。
通過以上分析可將前兩個子問題歸并為一類問題。
2.1 通路網圖層預處理
矢量軍事地形圖采用特定投影方式進行顯示,點用二維坐標表示。在點集中搜尋到某一點耗時最少的點本質上是一個對二維空間搜索的過程,在算法實現上需要計算點集中各個元素到該點的距離,然后在考慮地形地貌對軍事輪式平臺機動性能影響條件下,求出點集中各個元素到該點所耗費的時間,最后比較選出耗時最少的點。由于道路越平坦,表示道路所需的坐標點就越少,所以從平坦道路附近的起點尋找上路點時,會出現圖1(a)這樣不符合常理的現象。
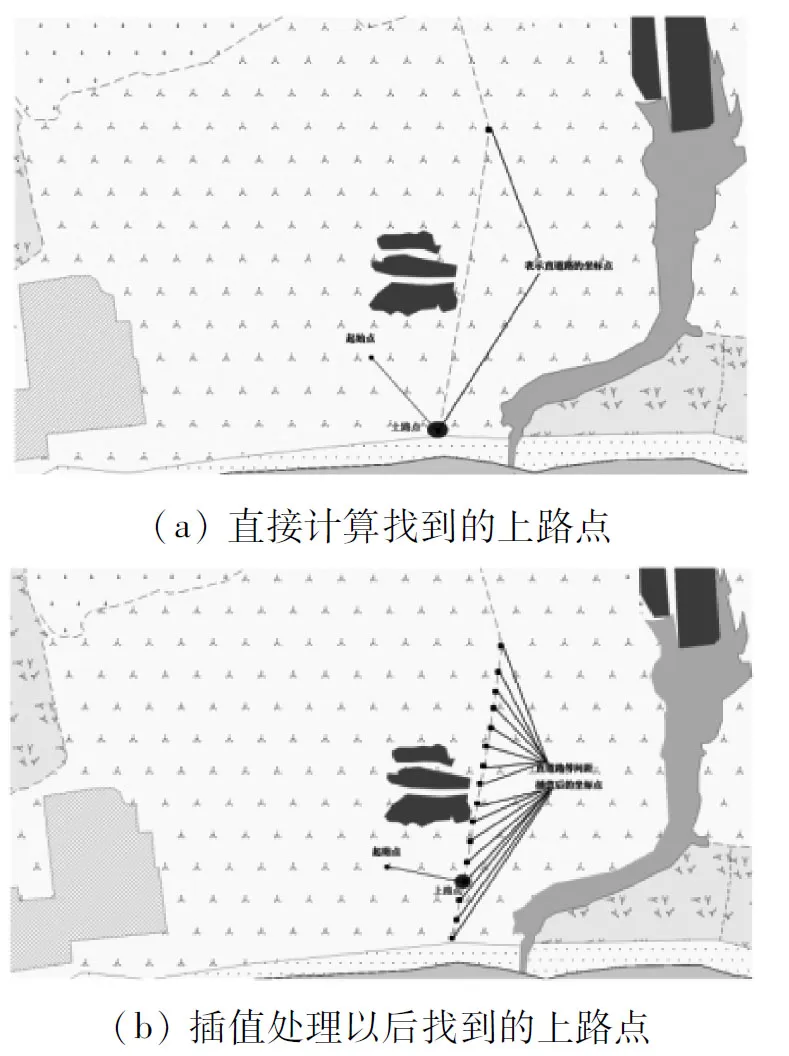
圖1 矢量地形圖上尋找上路點預處理過程
為解決這個問題,根據圖G上各條邊上相鄰坐標點之間的地理距離大小,按照某一適當間距進行插值,這樣雖表示各條道路坐標點的數量會增加,但卻可以較準確地計算出路外一點到道路的距離,見圖1(b)。
2.2 最優上路點、下路點算法
由于插值會導致搜索空間呈指數級增長,計算量大大增加,傳統算法對范圍較大、路網密集的地域,遍歷可能會導致系統運行緩慢、效率低下,Geohash是解決此問題的一個比較合適的空間點索引算法[14-15]。Geohash算法可以把二維的經緯度坐標編碼成一個字符串,把二維空間的點搜索問題轉化為一維的字符串匹配問題,其基本思想是將地球按某種投影方式展開為二維平面,將平面遞歸分解成更小的子塊,每個子塊具有相同的編碼;當需要查詢上路點時,先將起點的經緯度坐標按照Geohash編碼轉換成一個字符串,然后根據字符串匹配到所在的Geohash網格,然后按需要返回某些網格中的所有點,計算起點到返回的網格中的所有點的機動時間并排序,所需機動時間最小的那個點就是要找的上路點,見圖2。
具體步驟是:
Step1確定Geohash編碼的前綴長度m,判斷準則:m對應Geohash網格的較小邊長大于圓心所在地理位置的搜索半徑轉換成的經緯度跨度,且此時m是所有滿足條件的最大值,計算出搜索中心(上路點或下路點)所在的父級網絡編碼,即Geohash前綴編碼。
Step2提取交通圖層中所有的線元素,對線元素按合適間隔進行插值。
Step3建立指定編碼長度的交通路網圖層對應的Geohash網格圖模型。
Step4為防止一些在父級空間外且靠近其邊界的點被遺漏,進一步計算與父級網格相鄰的8個父級網格的Geohash前綴。
Step5對上述9個Geohash前綴網格分別遍歷基本Geohash空間,利用字符串前綴模式匹配,找到其對應的最優附近點及距離,按照與上路點或下路點地理距離的升序排列。
Step6逐個分析每個最優附近點所在網格地理環境,利用表1算出機動時間,取機動時間最小的點作為上路點或下路點。
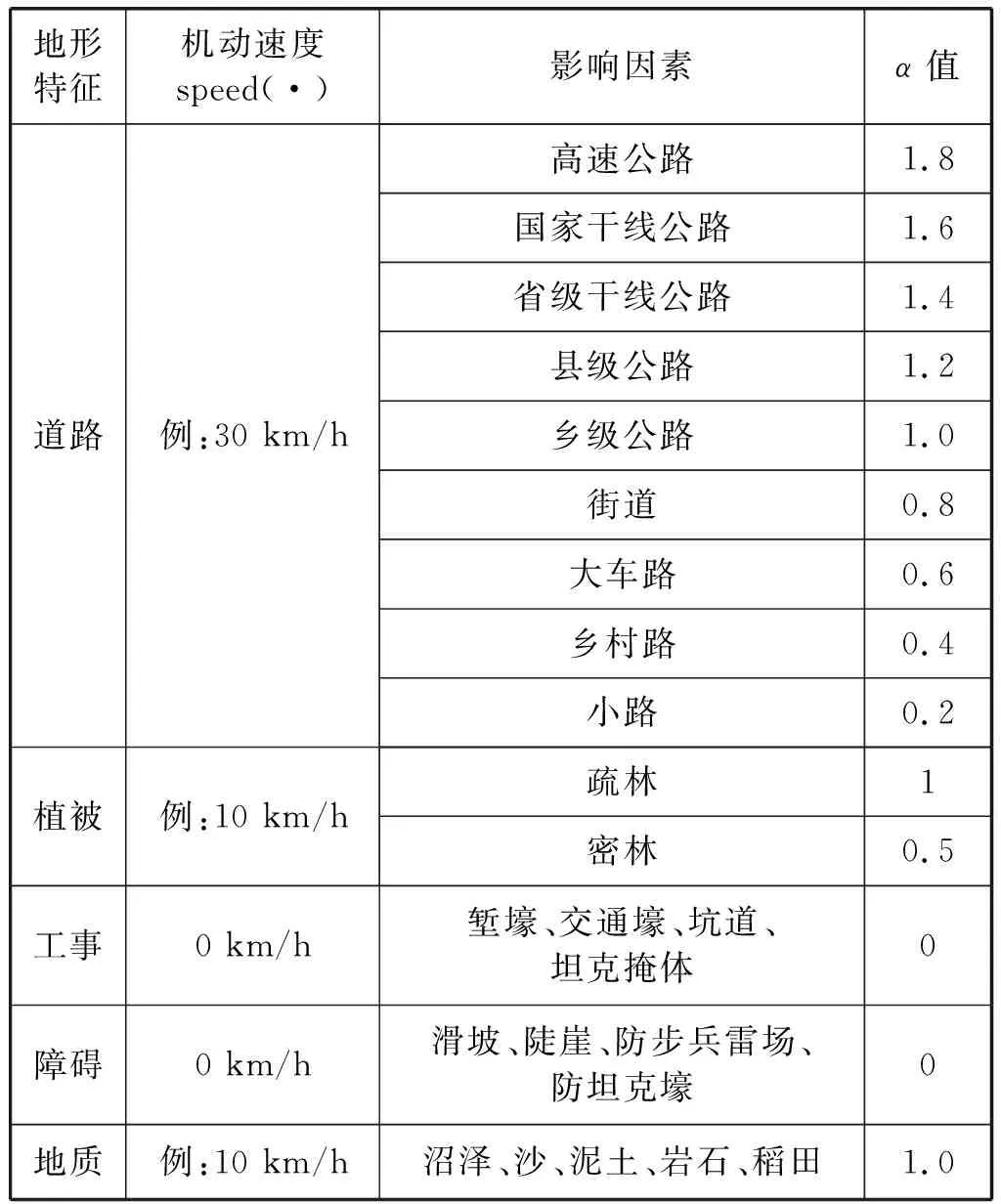
表1 地形地貌對速度的影響
2.3 改進的最短路徑算法
DAG圖每個弧段eij的時間權值wij與距離和速度有關系,而速度與該弧段的地形地貌道路等級有關,等級越高,軍事輪式平臺機動性越佳。作戰環境地形地貌對機動平臺的影響參考軍內標準,以軍事輪式車輛在鄉級公路上的行駛速度30 km/h為基準,用α表示道路地形地貌特征對速度的影響因子,兩者之間關系見表1。
設sij=α×30表示邊eij上軍事輪式平臺的機動速度,則權值函數wij可表示為:
wij=dij/sij
通過對交通路網圖層進行DAG建模(見圖3)、計算權值函數wij、修正Dijkstra算法,得到改進的最優路徑算法,具體描述如下:
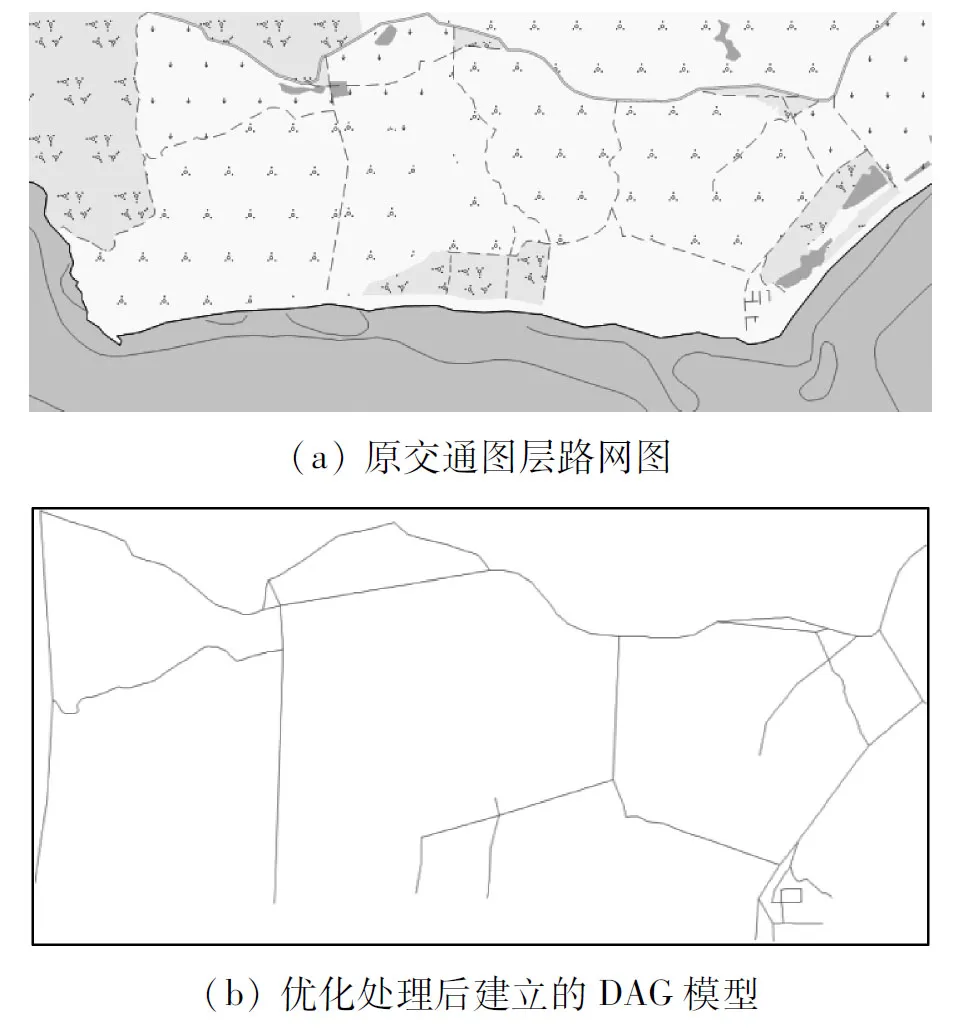
圖3 交通路網圖層DAG建模結果
Step1初始化:T(u)=0,μ(y,x)=0;R={u};S=Φ。
Step2在集合R中選取具有最小T標號的點y,則:
(1)S=S∪{y},R=R-{y};
(2) 如果e(y,x)∈E且x?S,則R=R∪{x}。
Step3若e(y,x)∈E,則:
條件1:若T(y)+w(y,x) 條件2:若T(y)+w(y,x)=T(x),則μ(y,x)=1。 Step4若所有點都進入集合S,算法停止,從圖G(V,E)中刪去所有μ(y,x)=0的邊,生成最短路徑圖G*,則從G*中源點u到終點v的任一條路徑都是最短路徑,T(v)是對應的距離值,也是從源點u到v的權值;否則轉入Step2。 時間復雜度:算法的運行時間表示為邊數和頂點數的函數,當采用鏈表或者數組來存儲所有頂點的集合時,算法的運行時間是O(n2)。 采用某省轄市路網數據,實驗平臺為C++和MGIS的二次開發,實驗硬件環境為CPU Intel(R) i7-3770 CPU 3.40 GHz,內存8 GB。考慮到信息安全敏感因素,從地圖數據中隱去一些相關的目標信息,為驗證算法可行性,分別設定起點、終點都在交通路網上、起點不在交通路網上、終點不在交通路網上、起點、終點均不在交通路網上四種情況,涵蓋連通與非連通兩種類,結果見圖4。 圖4 最優路徑搜索算法實驗結果 可以看出,本文綜合Geohash及Dijkstra算法,給出的改進的最優路徑算法,通過計算非連通交通網絡的最優路徑圖,有效解決了起點、終點不在交通路網上的非連通網絡機動路徑尋優問題,適用性廣,可直接應用于采用矢量軍事地形圖的戰術訓練模擬系統或仿真實驗系統中對輪式平臺的機動路徑進行規劃決策。 為證明改進后算法的優越性,與經典Dijkstra算法、標準A*算法進行搜索結果對比,矢量圖仍采用上述某省轄市路網圖,地形涉及疏林、密林、稻田、沼澤,共14 304條弧,8 730個頂點。為應用Geohash算法,對圖層中線元素以100米為單位進行打散、重構,區分起點、終點與路網連通特性4種情況,每種情況試驗若干次,統計最優路徑、搜索時間以及搜索結束后已標記頂點和已掃描頂點總數,結果見表2。圖5是其中一次應用本文所提算法獲得的一條最短路徑結果。 表2 最短路徑搜索算法性能比較 圖5 應用改進的最優路徑算法的結果 從實驗結果可以看出,情況①三種算法均能給出最短路徑搜索結果。標準A*算法由于采用柵格遍歷+啟發搜索方法,對于地理區域較大的網絡圖性能較差;經典Dijkstra算法與本文算法性能相當,但由于采用圖層預算處理技術;本文算法訪問頂點總數更少。 軍事輪式平臺機動路徑規劃是研制戰術訓練模擬系統、建設作戰仿真實驗系統的基礎。本文針對現有人在回路及作戰實驗計算生成機動路徑存在的問題,提出了一種基于Geohash及Dijkstra算法的改進的最優路徑算法,從起點、終點連通特性和圖論角度,分析了通過最優路徑規劃算法解決該問題的可行性及性能,實驗結果表明本文算法相比標準A*算法提高了搜索效率、降低了訪問頂點數目,且區域地理面積越大,優勢越突出。下一步將重點研究機動平臺在穿越交通道路網時,當道路出現不連續、不相交時,所提算法會出現失效的情況,從而提升算法柔性和解決問題范圍。3 路徑規劃問題分析與數學描述
3.1 問題分析
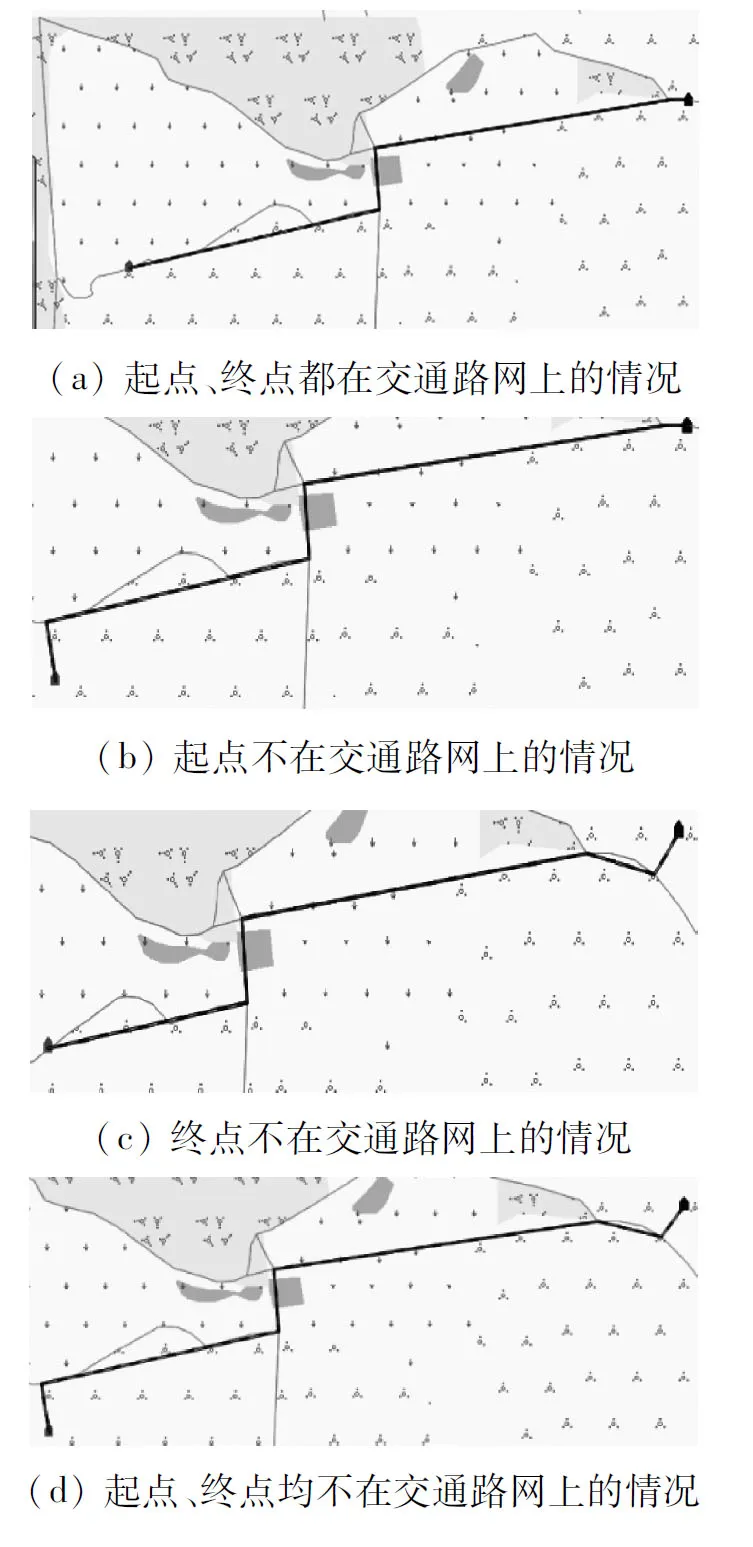
3.2 性能分析
4 結 語

