車聯網中時延感知的計算卸載和資源分配策略

江 帆,李 妍,宋琦琳

(1.西安郵電大學 通信與信息工程學院,陜西 西安 710121;2.西安郵電大學 陜西省信息通信網絡及安全重點實驗室,陜西 西安 710121)

車聯網(Internet of Vehicles,IoV)和自動駕駛是5G移動通信的代表性應用場景之一[1]。為了支持豐富的車輛服務應用,車載設備需要處理各種計算密集型任務。但是,車輛有限的任務處理能力和存儲空間難以應對愈發密集的計算任務需求[2]。為了改善上述問題,現有研究提出將基于移動邊緣計算(Mobile Edge Computing,MEC)的協作通信技術引入到IoV中,從而將計算任務卸載到網絡邊緣的服務器上,滿足車輛在運行過程中執行密集計算任務的要求[3-4]。

隨著無線通信技術的發展,車輛用戶以及處理任務的數量持續增加,對充分利用有限的頻譜資源提出了更高要求。為了應對頻譜資源匱乏的現狀,非正交多址接入(Non-Orthogonal Multiple Access,NOMA)技術和MEC技術的結合引起了較高的關注[5]。文獻[6]提出了一個混合型NOMA的卸載策略,有效降低了多用戶卸載的時延和能耗,但沒有考慮到MEC服務器有限的計算資源會影響卸載任務的執行時間。文獻[7]提出的優化策略考慮了任務卸載、計算資源分配等聯合優化問題,但忽略了周圍空閑的車輛資源。

一些研究引入了車到車(Vehicle-to-Vehicle,V2V)通信技術[8],通過將車輛用戶設備(Vehicle User Equipment,VUE)的一些計算任務卸載給鄰近負載較輕的VUE完成,在充分利用周圍閑置車輛資源的同時也減輕了MEC服務器的計算壓力。但是,采用V2V技術也出現了一些新的問題,如文獻[9-10]中涉及資源分配問題和頻譜復用引起的干擾問題。因此,在融合多種通信技術的車聯網中,研究合理高效的資源分配策略以支持車輛用戶的動態需求尤為重要。另外,由于無線通信環境的復雜多變,傳統優化策略復雜的計算步驟使得求解上述問題的效率較低,而機器學習算法相較于傳統方法能更高效地找到上述問題的最優解,例如文獻[6]中就使用了深度Q網絡(Deep Q-Network,DQN)算法為用戶選擇最優卸載策略,但DQN算法存在的過估計問題一定程度上影響了算法效率。文獻[11]中采用的深度競爭雙Q網絡算法(Dueling Double Deep Q-Network,D3QN)則可以減少DQN算法的過估計誤差,有效地提高了DQN算法的學習效率。

為了改善IoV卸載場景下的多維資源分配問題,擬提出一種時延感知的計算卸載及資源分配策略。首先,根據最大時延限制的要求,判斷一個計算任務是否需要卸載,然后通過支持向量機(Support Vector Machine,SVM)將需要卸載的計算任務按照時延和能耗的不同要求選擇MEC處理模式和V2V處理模式,并將網絡總成本構造為時延和能耗的加權和。最后,利用深度強化學習方法中的D3QN算法在不同的任務處理模式下分配計算或無線資源,最小化卸載過程中的總成本。為了驗證所提策略的性能,將其與同一系統模型下的基于DQN算法的資源分配策略、基于正交多址接入的資源分配策略和隨機資源分配策略等3種策略進行了對比。

1 系統模型及問題描述

1.1 系統模型

圖1 系統模型

假定每個VUE都有一個密集的計算任務要處理,表示為{Ti,Ci},其中Ti表示第i個VUE的任務大小;Ci表示計算1比特數據所需的CPU周期數。然后,根據最大時延限制需求將VUE分為本地組和卸載組。如果VUE能夠在最大允許時間內自己完成任務,就將其歸類于本地組,表示為l∈={I+1,I+2,…,M};如果VUE不能單獨完成任務,就將其劃分到卸載組,表示為i∈={1,2,…,I}。對于卸載組中的VUE,考慮了V2V和MEC兩種任務處理模式,由于MEC服務器計算能力較VUE更強,相同大小的任務在MEC服務器端的執行時延小。但是,一般情況下由于MEC服務器部署距用戶較遠,上傳任務時需要更高的發射功率,可能會造成卸載過程中更多的能量消耗。因此,假設任務對計算時延有更高的要求時會選擇MEC處理模式,否則將優先選擇V2V處理模式以減少能耗。這里用λ∈{0,1}表示卸載結果,λ=0表示MEC處理模式,λ=1則表示V2V處理模式。

1.2 計算模型

1.2.1 MEC處理模式

在MEC處理模式下,基于NOMA技術,多個VUE可以通過同一子信道將任務卸載給BS,然后BS側使用串行干擾消除技術對每個VUE的任務信息進行解碼。根據NOMA原理[5],第i個VUE向MEC服務器卸載計算任務時的信干噪比(Signal to Interference Plus Noise Ratio,SINR)的表達式為

(1)

式中:hi和hj分別表示從第i個VUE和第j個VUE到MEC服務器的信道系數;Pi和Pj分別表示第i個VUE和第j個VUE的發射功率;N0表示噪聲功率。在這里主要研究的是兩用戶NOMA系統,為了保證基站側接收功率的差異從而成功解調各用戶信號,采用了文獻[12]中所提出的均勻信道增益差配對策略(Uniform Channel Gain Difference,UCGD)選擇NOMA用戶。

第i個VUE將任務上傳到MEC服務器的傳輸時延的表達式為

(2)

式中:Ri=Blog2(1+ξi)表示從第i個VUE到MEC服務器的傳輸速率;B∈B1為MEC處理模式下的子信道帶寬。

相應的傳輸能耗表達式為

(3)

MEC服務器執行第i個VUE卸載任務的計算時延表達式為

(4)

式中,fi表示MEC服務器為計算卸載任務分配的相應計算資源。

第i個VUE在MEC服務器計算過程中的等待能耗為

(5)

由于計算結果通常比較小,返回結果時的相應時延和能耗可以忽略不計。因此,MEC處理模式下的總時延和總能耗分別表示為

(6)

(7)

為了同時滿足時延和能耗的約束,將卸載成本定義為時延和能耗的加權和,從而MEC處理模式下第i個VUE的總成本可以表示為

Ui=ωiDi+(1-ωi)Ei

(8)

式中,ωi是一個權重因子,表示不同的任務對時延和能耗的不同偏好,其取值在0到1之間。

1.2.2 V2V處理模式

(9)

從第i個VUE到第l個VUE的傳輸時延和能耗計算表達式分別為

(10)

(11)

考慮任務的優先級大小,假設V2V接收端在執行卸載任務之前優先執行自己的計算任務,第l個VUE完成其本地任務的計算時延為

(12)

式中,fl表示第l個VUE的計算資源。

第l個VUE完成卸載任務的計算時延和能耗的表達式分別表示為

(13)

(14)

式中,Pl=10-27(fl)2表示第l個VUE的電池功耗[14]。

根據以上假設,V2V接收端在處理完自身任務后才會選擇幫助其他VUE,即來自第i個VUE的計算任務在完成V2V傳輸之前無法被接收端第l個VUE處理。因此,V2V處理模式下的傳輸時延由第l個VUE的本地計算時延和第i個VUE到第l個VUE的傳輸時延之間的較大者確定。V2V處理模式下的總時延和總能耗的表達式分別為

(15)

(16)

同樣地,V2V處理模式下的成本函數可以表示為

(17)

基于以上分析,卸載過程的總成本表示為

(18)

1.3 問題描述

以最小化卸載過程的總成本為研究目標,旨在為每個VUE找到最優資源分配策略。因此,其優化問題可以構建為

(19)

由式(19)可以看出,總成本受到V2V對頻譜復用策略MEC計算資源分配策略的共同影響。但是,結合約束條件可以觀察到該資源分配問題是一個混合整數非線性規劃問題,傳統方法找到最優解的難度較大,而且難度也會隨著VUE數量的增加而增大。因此,采用了強化學習方法中的D3QN算法為每個VUE找到最佳的資源分配策略。

2 計算卸載和資源分配策略

提出的策略包括兩個階段:在第一階段,假設卸載任務可以通過時延需求和ω分為兩種處理模式,這是一個線性可分的二分類問題,因此采用SVM分類器實現該過程[15];在第二階段,根據分類結果,在不同的任務處理模式下利用D3QN算法完成相應的資源分配。

2.1 D3QN算法的基本要素

為了使用D3QN算法求解式(19)中提出的優化問題,首先將其與所提策略的資源分配場景相結合,以下給出了其相關元素的定義。

2.1.1 MEC處理模式場景

在MEC處理模式中,MEC服務器的計算資源首先被劃分為單位大小,然后分配給每個任務相應大小的計算資源。這種情況下的算法要素定義如下。

1) 智能體。在資源分配策略中,BS負責處理信令信息和分配資源,因此將BS定義為算法的智能體。

2) 狀態空間。選擇MEC處理模式的每個VUE為一個狀態,狀態空間被定義為所有選擇MEC處理模式的VUE,表示為s=[s1,s2,…,si]。

3) 動作空間。在MEC處理模式中,MEC服務器為卸載任務所分配的每一部分計算資源都可以被視為一個動作,因此,動作空間可以表示為a=[a1,a2,…,ai]。

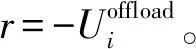
5) 策略。采取的是ε-貪婪策略,即每次選擇動作時以ε的概率隨機選擇動作,否則選擇最大Q值所對應的動作。

2.2.2 V2V處理模式

在V2V處理模式中,需要將上行鏈路資源分配給V2V鏈路,此處理模式下的相關定義如下所述。

動作空間:V2V處理模式中,每個動作為已經分配給其他VUE的上行鏈路資源,從而動作空間表示為a=[a1,a2,…,aM]。

智能體、獎勵和策略的定義與MEC處理模式中一致,此處不再贅述。

2.2 D3QN算法

基于以上定義,所采用的D3QN算法模型如圖2所示。

圖2 D3QN算法模型

由圖2可以看出,D3QN算法的具體改進內容如下。

1) 將DQN神經網絡的輸出層分為當前狀態值函數V(s)和動作優勢函數A(s,a)兩個支路,然后再將這兩個分支合并成Q值輸出[16]。其中,動作優勢函數是衡量當前狀態下采取不同動作時的相對價值。通過引入這個競爭網絡,可以分別平衡預測網絡和目標網絡中動作對Q值的影響,從而使智能體做出更準確的判斷。Q值的計算表達式為

(20)

式中:θ表示神經網絡參數;β和φ分別表示狀態值函數和動作優勢函數的神經網絡參數。

2) 為了避免DQN算法的高估問題,D3QN算法將動作選擇和Q值估計進行了解耦[17]。由預測網絡選擇下一個狀態下的動作,然后目標網絡評估該動作并計算相應的Q值。此時目標Q值的計算表達式為

(21)

具體來說,在算法實現過程中,設置一個循環周期有i步,每一步對應一個用戶使用上述貪婪策略獲取資源的過程,同時計算當前步的獎勵,然后將產生的交互數據存儲在一個經驗回放池中。經過數個時間步后,智能體將從經驗回放池中隨機抽取一小批經驗數據進行訓練,并更新網絡參數。通過不斷訓練神經網絡直到損失函數取得最小值,即算法達到收斂,此時對應的動作就是最優的資源分配策略。其中的損失函數定義為

Lt(θ)=E[(yt-Q(st-a,θ))2]

(22)

基于以上分析,基于D3QN算法的計算資源分配過程的偽代碼如算法1所示。

算法1 基于D3QN的計算資源分配算法輸入:MEC服務器的計算資源F1:初始化:經驗回放池D,預測網絡Q的參數θ,目標網絡Q′的參數θ′2:for episode=1,2,… do3:初始化st=[s1,s2,…,si]4:for t=1,2,…,i do5:以概率ε隨機選擇一個動作at6:否則選擇動作at=maxaQ(s,a;θ)7:執行動作at獲得獎勵rt(st,at),并轉移到下一狀態st+1,st=st+18:將(st,at,rt,st+1)存儲到經驗回放池D9:if經驗回放池容量達到閾值then10:從經驗回放池中隨機采樣一小批交互數據(st,at,rt,st+1)11:計算式(22)12:對于預測網絡參數執行梯度下降算法 13:每K步重設Q′=Q14:End if 15:End for16:End for輸出:資源分配結果

基于D3QN算法的無線資源分配過程與計算資源分配過程類似,這里不再贅述。所提時延感知的計算卸載和資源分配過程偽代碼如算法2所示。

算法2 時延感知的計算卸載和資源分配策略輸入:參數M,Ci,Ti,fi,DT1:for i=1,2,…,M do2:if (TiCi/f′i)≤DT then3:本地計算任務4:else SVM將需要卸載的任務分類5:if 第i個VUE選擇MEC處理模式6:選擇NOMA用戶對7:利用算法1分配計算資源8:MEC服務器完成計算任務9:else if 第i個VUE選擇V2V處理模式10:選擇V2V用戶對11:利用算法1分配無線資源12:V2V接收端執行計算任務13:End if14:End if15:End for輸出:處理模式的選擇結果,資源分配結果

3 仿真結果及分析

3.1 仿真參數

為了驗證所提策略的性能,將其與同一系統模型下的基于DQN算法的資源分配策略、基于正交多址接入的資源分配策略(Orthogonal Multiple Access,OMA)和隨機資源分配策略等3種策略進行了比較。仿真基于Python 3.8平臺完成,其中D3QN算法網絡模型采用了3個全連接層,并將第3個全連接層等分為狀態值函數層和動作優勢函數層;折扣因子為0.98;設置ε的值從0.08逐漸衰減至0.01,其余系統仿真參數如表1所示。

表1 仿真參數

3.2 結果分析

SVM的分類結果如圖3所示,可以看出參與任務卸載的用戶被訓練好的SVM成功分為了兩類。其中圓點表示選擇V2V處理模式的用戶,下三角表示選擇MEC處理模式的用戶。

圖3 SVM分類結果

為了驗證所采用D3QN算法的性能,將其和DQN算法的訓練效率進行了對比,具體如圖4所示。

圖4 D3QN和DQN算法的訓練效率對比

由圖4可以看出,隨著訓練次數的增加,DQN算法在大約1 100次后趨于穩定,而D3QN算法收斂于950次左右并且獲得的總成本更低。這是由于競爭網絡的引入、動作選擇與Q值計算的解耦都可以得到更準確的Q值,從而減少了無效的迭代訓練過程,提高了訓練的效率。

圖5對采用不同策略的時延進行了對比,以驗證所提策略對時延性能的提升。

圖5 不同策略的時延對比

由圖5可以看出,所提策略的累積時延均低于其他策略。首先,與隨機分配策略和基于DQN算法的策略相比,采用的D3QN算法在卸載用戶數逐漸增加時更有優勢,可以更高效地分配計算資源和無線資源,從而降低了卸載時延。其次,采用NOMA技術可以在同一子信道上同時完成兩個用戶計算任務的卸載,而OMA只能為一個用戶提供服務,從而有效地減少了時延。

為了驗證所提策略對吞吐量性能的提升,對不同策略的吞吐量累積分布函數(Cumulative Distribution Function,CDF)進行了對比,具體如圖6所示。

圖6 不同策略的吞吐量對比

由圖6可以看出,在相同概率下所提策略的吞吐量均大于其他策略。這是由于一方面D3QN算法可以有效地減少頻譜復用干擾,另一方面采用的NOMA技術可以通過功率域的非正交復用共享頻域資源,這兩種策略都可以顯著提高系統吞吐量。

圖7對不同策略下的總成本進行了對比,以驗證所提策略可以有效降低總成本。

圖7 不同策略的總成本對比

由圖7可以看出,隨著卸載用戶數的增加,所有策略的累計總成本也相應上升,但所提策略的總成本最低。這是由于所提策略在保證時延的同時,更好地平衡了時延和能耗,從而有效地降低了總成本。

4 結語

隨著IoV的快速發展,激增的數據量對車輛端的計算能力以及各種資源提出了更高的要求,因此推動任務卸載和資源分配等技術的發展至關重要。針對該問題,提出了時延感知的計算卸載和資源分配策略。在所提出的策略中,首先利用SVM將卸載任務按照時延和能耗的要求分為MEC處理模式和V2V處理模式兩類,每個VUE可以選擇相應的任務處理模式。此外,為了進一步降低卸載傳輸時延,在MEC處理模式中采用了NOMA技術。最后,為了最小化卸載過程中的總成本,采用了D3QN算法在各處理模式中分配計算或無線資源。仿真結果表明,與現有的基于DQN算法的資源分配策略、基于OMA的資源分配策略和隨機資源分配策略相比,所提的策略不僅優化了VUE卸載過程中的時延和吞吐量性能,還有效降低了系統卸載的總成本。