基于燃油經濟性的坡道適應性巡航控制研究

唐榮江,李蒙康,畢道坤,張致遠,周輝

(1.桂林電子科技大學機電工程學院,廣西 桂林 541004;2.吉林大學汽車工程學院,吉林 長春 130012;3.東風柳州汽車有限公司商用車技術中心,廣西 柳州 545005)

商用車作為貨物運輸的重要途徑,在生產生活中占據越來越重要的地位,在以降低能源消耗和環境保護為主題的時代,提升燃油經濟性成為商用車領域主要研究方向之一[1]。

適應性巡航控制由定速巡航發展而來,主要以安全性與舒適性為主要研究熱點[2]。我國地形以山地丘陵居多,起伏的道路勢必導致車輛燃油消耗的提高,研究表明,相比平坦道路,在丘陵地區車輛的燃油消耗要高出5%～20%[3]。車輛通過坡道路面時,車輛的燃油經濟性不僅與自身運行狀態密切相關,且在很大程度上還與駕駛員對車輛的操作行為有關,不合理的加速、減速都會造成油耗的增加[4]。因此,考慮坡道信息的適應性巡航控制,對提升商用車的燃油經濟性有重大意義。

Erik Hellstr?m[5]基于最優巡航控制開發了預測性經濟巡航速度控制器,借助車載GPS系統和坡度數據庫獲得道路幾何信息,將此前瞻性信息用于預測性優化速度軌跡,該經濟巡航控制系統既保證了乘客舒適度,也降低了車輛燃油消耗量。周敏[6]對自動變速巡航控制的汽車在通過坡道路面時的整車燃油經濟性進行研究,采用動態規劃算法規劃了車輛在坡道上行駛的最合理速度軌跡,通過仿真驗證,所提出的考慮坡道的巡航控制大幅度提升了車輛燃油經濟性指標,同時充分保證駕駛時間和舒適度。D.Jia[7]提出一個增強的PCC系統,集成了數據驅動的流量預測模型和瞬時控制算法,計算瞬時最佳速度曲線,以最小化能量消耗行駛。Y.Lin[8]基于全球定位系統(GPS)和地理信息系統(GIS)提出基于上下坡道路的經濟巡航控制系統,將數字道路地圖的道路高程剖面與非線性預測控制策略相結合,根據道路等級提供經濟速度,不僅可以為駕駛員提供經濟駕駛指導,還可以實現駕駛安全。

車輛縱向運動具有非線性、時變性和不確定性等特點,研究對象為“人—車—環境—任務”的多元耦合系統。本研究提出了一種基于道路地形信息、車輛動力學模型和燃油消耗模型的非線性預測控制的坡道適應性巡航控制方法,在確保車輛行車安全性的前提下,提高車輛的道路適應能力,避免車輛頻繁的加速和減速行為,實現車輛的縱向自動控制,提高燃油經濟性。

1 適應性巡航控制系統總體方案

車輛行駛過程中,在沒有橫擺運動的前提下,僅需要對車輛縱向運動進行控制,采用經典的上下層控制結構。上層控制系統通過車輛運行狀況和當前行駛的道路工況,基于極小值原理對快速優化的非線性模型預測控制算法進行求解,以最優控制變量的求解方程獲得前方道路坡度的縱向需求扭矩的最優控制序列,輸出車輛的期望扭矩給下層控制系統。下位控制系統運用逆縱向動力學模型輸出期望油門開度α,利用油門開度控制車輛縱向動力學模型,控制加速或減速,實現車輛坡道適應性巡航控制系統的功能。坡道適應性巡航控制系統總體方案見圖1。

圖1 適應性巡航控制系統的總體方案

2 車輛系統建模

2.1 道路工況

考慮到仿真工況的普遍適用性,參考我國的實際地形特點,尤其南方一些丘陵地帶的典型道路,常伴隨有一定的坡度,并根據國家道路標準,道路坡度設計的極限值范圍在-10%～10%之間。利用TruckSim動態系統仿真軟件,搭建虛擬道路工況,模擬真實的行車工況進行仿真,采用兩種仿真工況進行仿真分析：一種場景為正弦函數模擬典型的單一上坡道路、上下坡道路工況;另一種場景選取柳州到貴港高速公路其中一段的真實道路作為研究工況。

2.2 縱向動力學模型

對車輛縱向動力學進行分析,可建立縱向動力學方程,其表達為

(1)

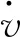
驅動力由發動機扭矩提供,其表達式為

(2)

式中：Te為發動機的輸出扭矩;it=ig·i0,為傳動系統總變速比;η為傳動系效率;r為輪胎半徑。

坡道阻力為

Fi=mgsinα。

(3)

式中：g為重力加速度;α為道路坡度。

空氣阻力為

(4)

式中：CD為空氣阻力系數;A為迎風面積;ρ空氣密度;v為車速。

滾動阻力為

Ff=fmgcosα。

(5)

式中：f為滾動阻力系數。

2.3 燃油消耗模型

車輛在道路上行駛時,建立滿足非穩定工況的瞬態油耗預測模型,準確估計車輛在穩定和非穩定工況下的燃油消耗。基于瞬態修正的多項式油耗模型建模思路,利用多項式油耗模型對燃油消耗率與扭矩和發動機轉速之間的關系線性建模,并利用瞬態燃油變量對穩態模塊進行修正。

建立穩態油耗模型,其表達式為

mf=f(ne,Te)=b1+b2ne+b3neTe+b4ne2Te。

(6)

式中：mf為穩態燃油消耗率;b為油耗模型參數;ne為發動機轉速。

分析燃油消耗的差值與發動機扭矩變化率之間的關系,發現燃油消耗差值與發動機扭矩變化率基本呈線性關系,其表達式為

(7)

式中：Δmf為燃油消耗差值;km,tm為待定系數。

綜合瞬態修正模塊和穩態油耗模型,建立瞬態修正的多項式燃油消耗模型,其表達式為

(8)

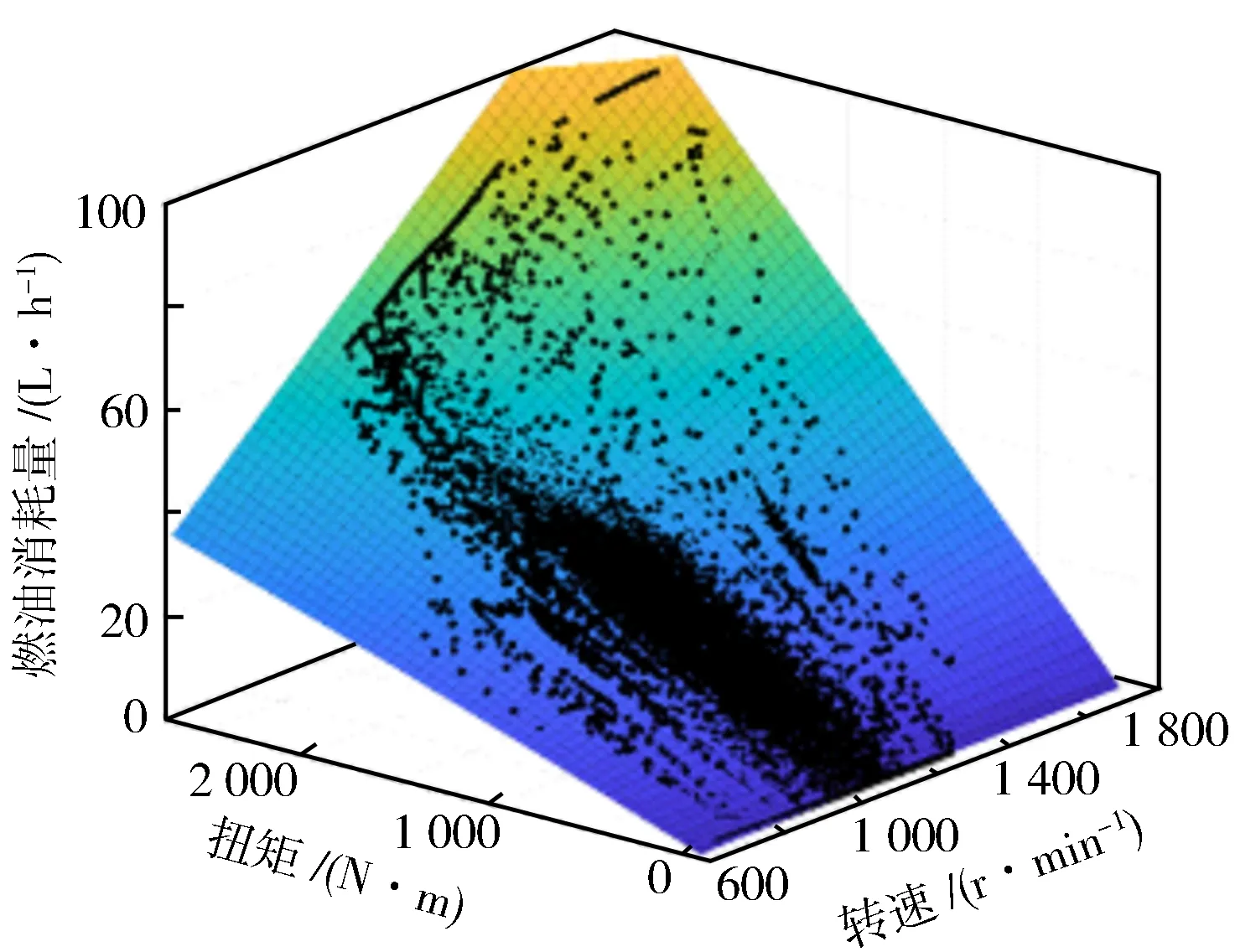
圖2 燃油消耗率擬合圖

通過實車試驗,分析采集的油耗數據,利用最小二乘法,擬合燃油消耗模型,選取其中預測精度最優的模型為本研究油耗模型。燃油消耗率的擬合性能見圖2。

3 適應性巡航控制系統的設計

車輛行駛過程中,實際道路工況千變萬化,坡道適應性巡航控制應具備合理控制巡航需求扭矩的能力。適應性巡航控制采用分層控制結構,上層控制系統結合前方道路工況和相關車輛信息進行分析,規劃出車輛需求發動機扭矩;下層控制系統通過車輛逆縱向動力學模型輸出期望油門開度,由油門控制器實時控制車輛。

3.1 上層控制系統設計

3.1.1 系統方程建模

車輛建模僅考慮車輛的縱向運動,假設與其他車輛沒有相互作用。建立被控系統的縱向控制模型,假設車輛在任何時刻t的狀態方程為

(9)

式中：x,u分別為控制系統的狀態量和控制量。

車輛發動機扭矩與控制輸入有關,即Te(t)=u(t);x(t)=[x1(t),x2(t)]T,x1,x2分別為主車輛t時刻的當前位置與速度。

改寫車輛的狀態方程為

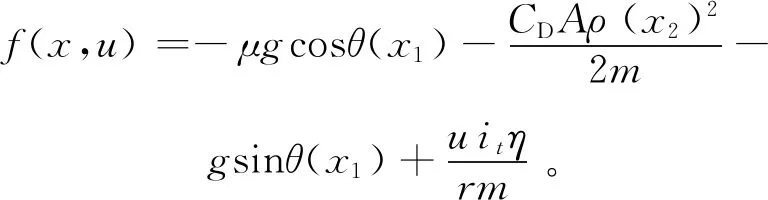
(10)

車輛加速和減速與發動機扭矩的變化直接相關,為了考慮巡航控制系統中的平順性問題和駕駛員行為的任何異常,重新定義與控制輸入相關的不等式約束,引入虛擬輸入ud,表示為

(11)

為了優化車輛控制輸入,解決最優控制問題,則需建立性能指標函數,評價控制效果優劣。其表達式為

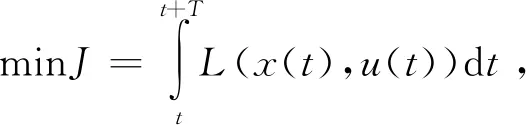
(12)

(13)

式中：成本函數L為車輛單位距離所消耗的燃油量。

利用拉格朗日乘子法推導最優控制輸入,并引入哈密頓函數：

H(x,λ,u,ψ)=L(x,u)+λTf(x,u)+ψTC(x,u)。

(14)

式中：λ為協態因子;ψ為與約束相關的拉格朗日乘子。

3.1.2 最優控制離散化

滾動時域控制本質上是一系列連續時間內的時域最優控制問題。將預測范圍T分為N個步驟,步長為Δt=T/N,其中i=0,…,N-1表示所述預測視界中第i個實例處的相應值。

電子地圖能夠預知前方道路信息,利用前向歐拉方法對任意位置的道路坡道角θ離散計算,其表達式為

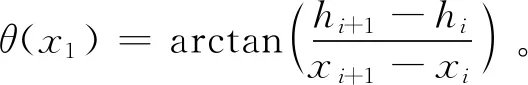
(15)

式中：θ(x1)為第i階段道路坡道角;hi與hi+1分別為第i階段與第i+1階段的海拔;xi與xi+1分別為第i階段與第i+1階段的位移。

離散化最優控制問題可以表述如下：

minimize：

(16)

Subject to：

xi+1(t)=xi(t)+f(xi(t),ui(t))Δt。

(17)

上述離散化非線性代數方程,基于隱函數的離散極小值原理,對離散化最優控制問題進行求解,將泛函條件極值問題轉化為無約束的泛函極值問題,可得到廣義泛函極值的必要條件。

x(t),λ(t)需要滿足的邊界可以表述如下：

x(t0)=x0,

(18)

(19)

最優控制的必要條件可以概括如下：

Hu(xi(t),λi(t),ui(t),ψi(t))=0,

(20)

(21)

3.2 下層控制系統設計

汽車在行駛過程中,其輸出扭矩與油門開度、發動機轉速有關,通過TruckSim軟件提取發動機的MAP圖(見圖3)。

由發動機MAP圖構建發動機扭矩、轉速與油門開度的對應關系：

α=f(ne,Te)。

(22)

式中：α為油門開度;f(ne,Te)為逆發動機扭矩特性曲線。若通過車輛的狀態和當前道路工況得到發動機期望扭矩Te和發動機轉速ne,則可通過二維查表法得到此工況下對應的期望油門開度。

圖3 發動機MAP圖

4 聯合仿真

MSC TruckSim是動態模擬整車動力學仿真軟件,從人、車、路、項目、事件等多個方面入手,對基本的各項試驗進行仿真,從而分析車輛的各項性能。搭建整車模型,設置駕駛員行為和道路行駛工況、行駛路面條件、輸入輸出信號、仿真時長和頻率,導入Simiulink中得到聯合仿真的車輛模型。在TruckSim軟件中設置車輛的主要參數,如表1所示。在Matlab/Simulink平臺上搭建的商用車坡道適應性巡航的聯合仿真模型見圖4。

表1 車輛主要參數

圖4 Simulink與TruckSim聯合仿真模型

5 系統仿真驗證

為了進一步評估所提出的坡道適應性巡航控制的節能性能,建立虛擬道路仿真工況,分別在單一上坡道路工況、上下坡道路工況、真實道路工況進行聯合仿真試驗。車輛的初始巡航速度設定為75 km/h。

5.1 上坡道路工況仿真

在總長度1 200 m、最大坡度4.5%的單一上坡道路工況進行聯合仿真,結果見圖5。

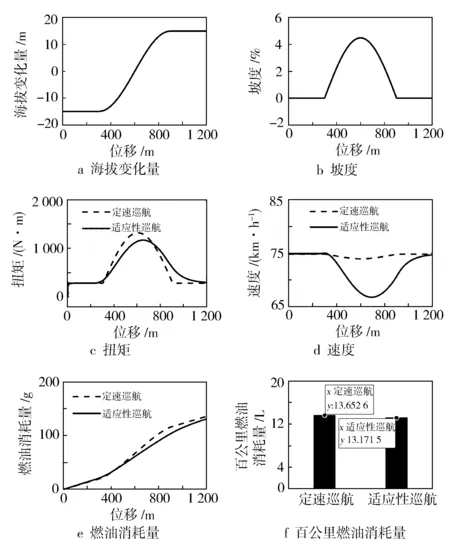
圖5 上坡工況仿真結果

海拔變化范圍為-15～15 m,坡度范圍為0%～4.5%,由需求扭矩變化曲線可知,車輛在上坡前需求扭矩增大,適應性巡航控制車輛在上坡路段前發動機提高扭矩,積蓄能量,上坡過程中根據車輛前方道路坡度的大小,使發動機工作在燃油經濟性最優扭矩。比較速度變化曲線可知,定速巡航一直穩定在規定速度行駛,適應性巡航速度隨坡度的改變而變化。由圖5e知,定速巡航的總燃油量為135.98 g,適應性巡航的總燃油量為131.19 g,適應性巡航的燃油消耗量增長緩慢。通過比較圖5f百公里燃油消耗量可知,坡道適應性巡航控制比定速巡航控制節省約3.52%的燃油。

5.2 上下坡道路工況仿真

上下坡道路工況的聯合仿真道路總長度為2 400 m,最大坡度為2.5%,仿真結果見圖6。

由圖6可知,海拔呈正弦函數變化,在上下坡道路工況中,選取海拔變化范圍為-7.5～7.5 m,坡度范圍為-2.5%～2.5%。由圖6c知,在進入下坡前,需求扭矩降低,提前輕微減小油門開度,進入下坡時,使其車輛穩定工作在燃油經濟性最優扭矩,利用下坡優勢和動能與重力勢能轉換,減少了能量損耗。由圖6e知,定速巡航的總燃油量為169.027 g,適應性巡航的總燃油量為164.587 g。圖6f為百公里燃油消耗量的比較,提出的坡道適應性巡航控制算法比定速巡航控制節省2.62%的燃油。

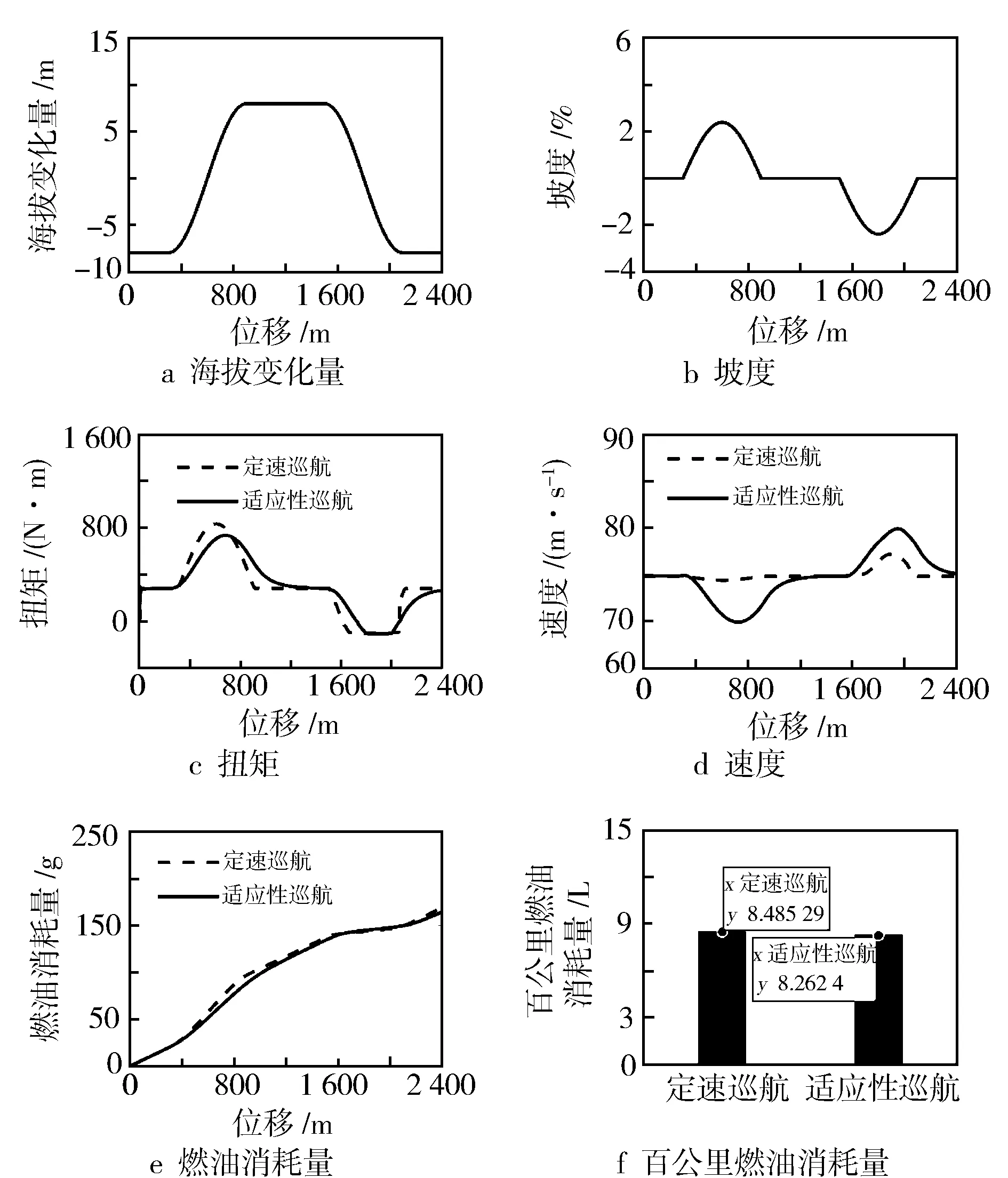
圖6 上下坡工況仿真結果

5.3 實際道路工況仿真

作為對比驗證,基于實際道路評估所提出的坡道適應性巡航控制系統的有效性。選取柳州到貴港的一段真實道路,長為3 000 m,比較結果見圖7。

真實道路的坡度范圍在-4%～2.2%。由圖7可知,定速巡航的總燃油量為205.323 g,適應性巡航的總燃油量為199.5 g,通過比較百公里燃油消耗量,可知提出的坡道適應性巡航控制算法比定速巡航節省約2.84%的燃油。

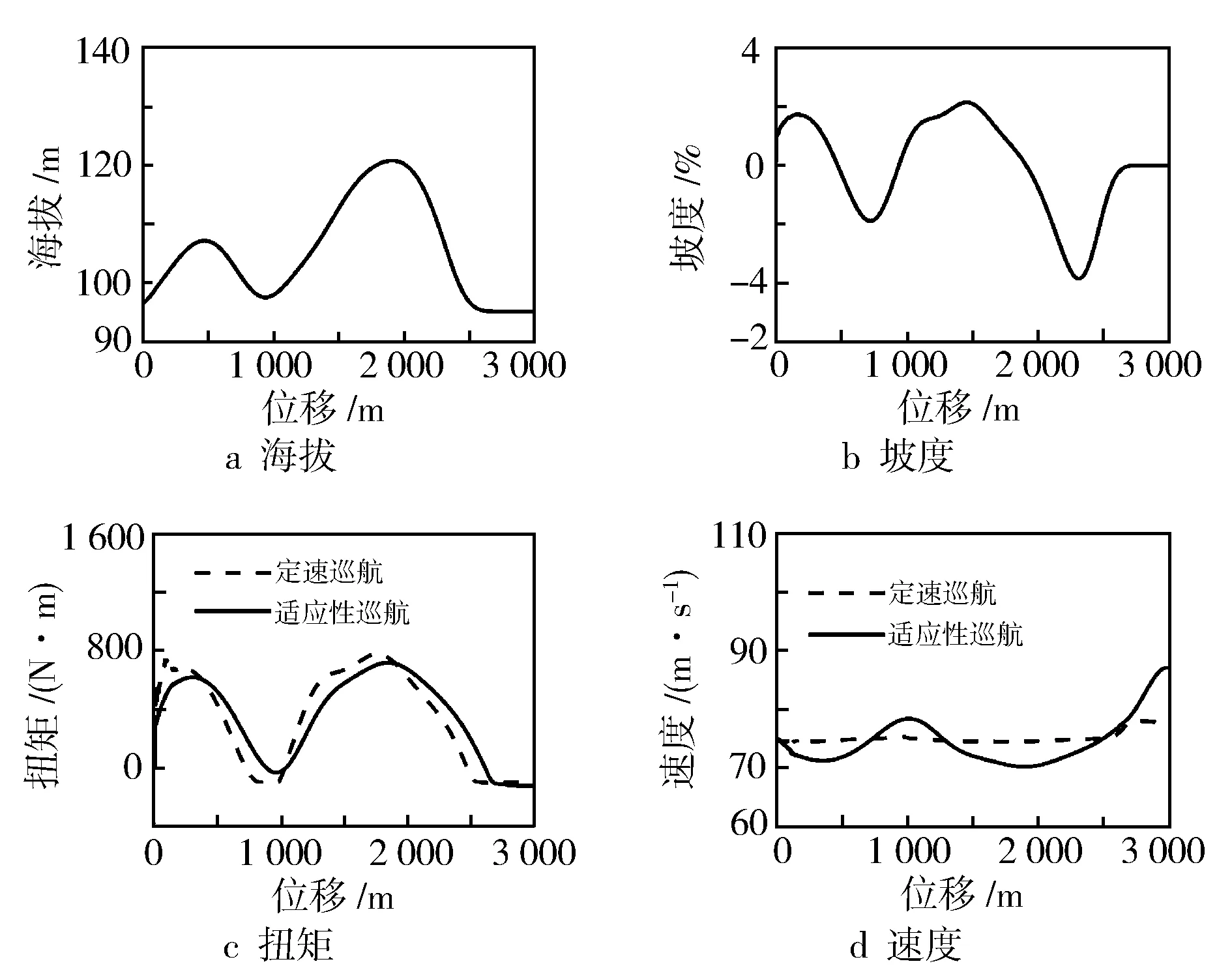
圖7 真實道路工況仿真結果

6 結束語

提出了商用車坡道適應性巡航控制的燃油經濟性仿真模型,研究車輛在穩定和非穩定工況下的燃油消耗模型、坡度變化、行駛工況對燃油經濟性的影響。針對坡道巡航的燃油經濟性問題,基于Trucksim和Simulink軟件對開發的坡道適應性巡航控制系統進行聯合仿真并驗證。從仿真結果可知,在上坡前,車輛通過提前輸出油門開度,積蓄能量,避免上坡過程中出現急減速;進入下坡時,在沒有任何制動的情況下,提前減少油門開度,利用下坡的優勢,充分利用動能與重力勢能轉換,減少能量損耗。

在虛擬道路仿真工況和真實道路仿真工況下,與傳統定速巡航控制相比,坡道適應性巡航控制平均節油效果達到約3%,有效降低了燃油消耗量。