考慮緊迫度的應急物資軸輻供需網絡優化研究

仲舒琳， 倪 靜

（上海理工大學管理學院， 上海 200093）

0 引 言

近年來，世界各地突發性公共衛生事件頻發，給人類帶來了難以估量的災難，如SARS、甲型HIN1、非洲豬瘟以及COVID－19［1］。 由于該類事件通常具有突發性，受災地的應急物資在爆發初期往往是不夠的，需要從外部進行應急物資調度，高效的應急物資調度網絡設計在事件中發揮著重要的作用。

應急物資調度問題是近年來的研究熱點之一，Ding［2］構建了基于灰色區間的多個需求點到多個供應點間的應急物資調度，采用NSGA－II 算法，有效減少了包括應急響應系統的時間成本損失在內的總成本；張琳［3］在考慮不確定條件下，構建調度時間最短和調度成本最低的兩目標應急物資調度模型，通過LINGO 對其求解，結果表明該模型可以有效合理的進行應急物資調度；王付宇［4］考慮災害初期道路通行和運輸能力的限制，構建災區平均等待時間最短和物資調度成本最小的雙目標優化模型，并通過改進的NSGA－II 算法驗證了模型的有效性。

上述研究主要聚焦在物資調度的時效性和經濟性，沒有考慮到需求點間存在的差異性。 胡曉偉［5］以需求滿足率最大為主要目標，兼顧車輛行駛距離，構建應急醫療物資動態分配模型，并通過算例驗證了模型的有效性和可行性；單子丹［6］考慮物資需求的緊迫性，構建集散－中心－需求點三級調度網絡，有效的緩解資源短缺情況、提高醫用物資利用率；趙建有［7］引入受災點緊迫度量化及分級，構建多目標車輛路徑優化模型，滿足應急物資配送的時效性、經濟性與公平性；劉艷秋［8］在考慮物資分配公平性的情況下，同時考慮道路受損情況，構建應急物流路徑優化的兩階段模型，并通過一種混合人工魚群算法求解證明了模型的可行性。

在供需網絡中有些研究考慮三級供應鏈，供應點－中心－需求點，卻忽略了中心之間的物資運輸功能，軸輻式網絡通過中心軸點間進行連接，形成規模運輸，因此軸輻網絡通過在軸點間進行資源整合，從而有效提高資源調度效率。 Zhou［9］考慮客戶差異化服務需求，構建了多式聯運的軸輻式網絡模型，獲得了總成本最小的最優樞紐位置和分配方案；黃星［10］在模糊籌集時間下構建出具有直達結構和Hub 結構的混合協同籌集的軸輻式應急物資籌集網絡，有效的運用于震災應急物資籌集決策中；Li［11］在COVID－19 背景下基于軸輻式網絡考慮多類型緊急救援，建立了以運輸時間消耗和運輸成本最小化為目標的雙目標優化模型，有效的兼顧了時間和成本。

目前，國內外對于應急物資調度的研究已有一定的基礎，對公平性的實現主要集中在對物資數量公平性研究上，較少考慮物資分配和時間調度的雙重公平。 因此，在突發公共衛生事件下，本文考慮需求點緊迫度，兼顧時間公平和分配公平，構建應急物資供需網絡模型。 另外，在應急物資調度網絡中，為了提高物資調度效率，采用軸輻式網絡可以通過軸點間的鐵路進行快速運輸，并通過多式聯運靈活高效地進行物資調度，因此本文構建考慮緊迫度的應急物資軸輻供需網絡模型。

1 問題描述

本文主要研究應急物資調度網絡問題，并以最小化物資缺口，最小化時間延誤，最小化系統總成本為目標構建網絡。 在物資調度過程中，由于突發公共衛生事件初期供應有限，無法滿足所有需求點的物資需求，通過衡量需求點間存在差異性評價需求點緊迫度，將物資進行合理分配以滿足物資分配的公平。 在此基礎上依據軸輻式網絡結構特點構建應急物資供需網絡，該應急物資軸輻供需網絡中有3類節點：供應點、中轉樞紐、需求點，軸輻式網絡拓撲結構如圖1 所示。 供應點和需求點作為軸輻網絡中的輻點，中轉樞紐作為網絡中的軸點，軸點與輻點之間通過靈活性高的公路運輸，軸點間則采用速度更快經濟性更高的鐵路運輸，并且允許輻點直接運輸，構建多式聯運的混合軸輻應急物資供需網絡，旨在快速高效地對需求點進行大規模的物資輸送。

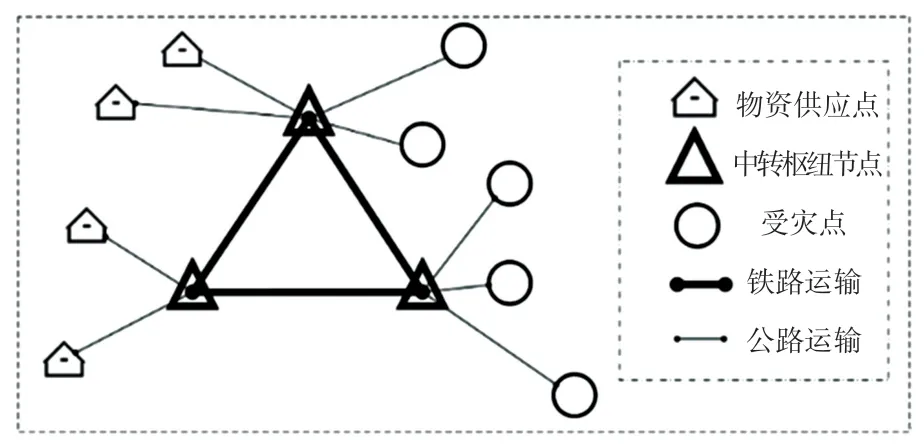
圖1 軸輻式網絡拓撲結構Fig. 1 Hub－and－spoke network topology

2 物資調度模型

基于問題及分析，本文構建的考慮緊迫度的應急物資軸輻供需網絡模型。

2.1 模型構建

假設突發公共衛生事件發生時， 供應點i（i∈I） 為需求點j（j∈J） 提供物資供應，運輸方式為通過樞紐點k、m（k，m∈K） 中轉運輸或者直達運輸。

首先，在考慮需求緊迫度的情況下構建公平性函數F1，式（1）：

其中，λj為需求點j的需求緊迫度；qj為需求點j需求的物資量；qij為供應點i向需求點j實際分配的物資量。

其次，在考慮需求緊迫度的情況下構建時效性函數F2，式（2）：

其中，Tijkm為供應點i經過樞紐點k，m到達需求點j的時間；Xijkm為0－1 變量，判斷是否存在路徑將物資通過樞紐k，m送至受災點，存在則為1，否則為0；RTj為需求點j可接受的最晚物資到達時限；

然后，構建系統經濟性函數F3，式（3）：

其中，Xik為0－1 變量，判斷供應點i是否隸屬于樞紐k，是則為1，否則為0；Xkj為0－1 變量，判斷需求點j是否隸屬于樞紐k，是則為1，否則為0；Xijkm為0－1 變量，判斷是否存在路徑將物資通過樞紐k，m送至受災點，是則為1，否則為0；Yij為0－1 變量，判斷供應點i是否直接向需求點j運輸物資，是則為1，否則為0；dij為從供應點i到需求點j之間的距離；dik為從供應點i到樞紐點k之間的距離；dkm為從樞紐點k到樞紐點m之間的距離；dmj為樞紐點m到需求點j之間的距離；Cij為供應點i與需求點j兩地之間的單位運輸成本；Cik為供應點i與樞紐點k兩地之間的單位運輸成本；Ckm為樞紐點k、m兩地之間的單位運輸成本；Cmj為樞紐點m與需求點j兩地之間的單位運輸成本；αkm為經過樞紐點k，m運輸的干線折扣率；uk為樞紐點的單位裝卸費用；

最后，進行約束條件設置：

判定是否存在物資運輸從供應點i經過樞紐點k、m最終到達需求點j，式（4）：

其中，Xkk為0－1 變量，判定樞紐點k是否被選作中轉樞紐，是則為1，否則為0。

運輸方式只有轉運和直達兩種運輸方式，式（6）：

一個供應點i只能被分配給一個樞紐點，式（7）：

一個需求點j只能被分配給一個樞紐點，式（8）：

只有樞紐k被選作樞紐點才能為供應點i服務，式（9）：

只有樞紐k被選作樞紐點才能為需求點j服務，式（10）：

表示運輸決策直達的判定方式，式（11）：

其中，v為運輸工具的運輸速度；v1為公路運輸；v2為鐵路運輸。

物資從供應點i最終到達需求點j的時間，分為3 種：經過兩個不同樞紐點k、m到達需求點j，經過一個樞紐點k到達需求點j，直接到達需求點j，式（12）：

其中，rk為在樞紐k的單位貨物進行中轉的時間。

供應點i給需求點j的物資供應量滿足需求點j的最低物資滿足量，e為緊迫度分級后的最低滿足率，式（13）：

式中：e為需求點的最低滿足率，I 類需求點的最低滿足率e1＝0.7，II 類需求點的最低滿足率e2＝0.6，III 類需求點的最低滿足率e3＝0.5。

需求點j的物資滿足量不超過其需求量，式（14）：

供應點i的供給量不超過其可供應量，式（15）：

其中，qi為供應點i可供應物資量。

2.2 需求緊迫度評價指標體系構建

由于重大傳染病疫情的突發性和擴散性，需要快速進行疫區救援。 而在疫情初期，醫療應急物資、應急救援人員及運輸工具等資源往往無法滿足所有需求點的需求，加之需求點之間存在感染情況和醫療水平的差異性，需求點對于物資需求量和時間也有區別。 為了保障疫區的各需求點的公平性，需要考慮各需求點之間的差異，綜合評價需求點的應急物資需求緊迫度，在資源供應不足的情況下最大化有限的應急物資的效用，更好地控制疫區疫情擴散。

需求緊迫度評價指標一般包括受災人員的數量、基礎設施的損壞程度及物資儲備等情況，本文結合傳染病疫情選取潛在擴散風險、疫情感染情況、城市自救能力這3 個關鍵因素作為的一級指標，并在每個一級指標下選取多個二級指標，構建需求點緊迫度評價指標體系見表1。

表1 需求點緊迫度評價指標體系Tab. 1 Evaluation index system for the urgency of demand points

2.3 基于熵值－TOPSIS 確定需求緊迫度

熵值法是一種客觀評價方法，根據數據本身的信息來確定客觀權重，可以避免人為主觀因素導致的偏差［12］。 TOPSIS 法是對方案進行多目標決策的常用方法，通過比較目標方案與正負理想解的距離進行方案排序［13］。 本文通過熵值法確定各評價指標的權重，并通過TOPSIS 法對需求緊迫度系數進行計算，熵值－TOPSIS 法的計算步驟如下：

2.3.1 熵值法

步驟1建立指標矩陣

將m個需求點的n個影響因素指標數據處理成矩陣Xij代表第i個需求點的第j個影響因素指標數據的值（i≤12，j≤7）；

步驟2數據標準化

為了消除數據的量綱影響，需要對數據進行標準化處理，本文涉及兩種類型的數據：效益型指標和成本型指標。 效益型指標代表其指標與評價結果正相關，式（16）：

成本型指標代表其指標與評價結果負相關，式（17）：

步驟3計算第j項指標下第i個需求點占該指標的比重Pij，式（18）：

步驟4計算第j個指標的熵值Ej，式（19）：

步驟5計算差異系數Gj，式（20）：

步驟6確定各項評價指標的權重Wj， 式（21）：

2.3.2 TOPSIS 法

步驟1對評價指標矩陣進行歸一化處理，rij為歸一化后各指標的值，式（22）：

步驟2將rij與熵值法得到的權重Wj進行加權操作得到vij，式（23）：

步驟3計算正理想解A＋， 負理想解A－， 式（24）和式（25）：

步驟4計算各需求點j到正理想解的距離，到負理想解的距離Di－，式（26）和式（27）：

步驟5計算各需求點i的相對貼近度Ci，該結果作為需求點的緊迫度值，式（28）：

3 改進NSGA－II 算法

本文考慮的需求緊迫度的應急物資供需網絡模型是一個高復雜度、多約束、多目標的優化問題，屬于NP－Hard 難題，對于此類問題傳統的精確算法難以獲得理想的結果。 NSGA－II 算法是在遺傳算法（GA）的基礎上通過增加快速非支配排序、擁擠度距離比較和精英保留策略，是經典的已被廣泛應用于解決多目標問題的方法［14］。 但是傳統的NSGA－II算法在種群分布性和多樣性有所缺陷，因此本文采用改進的NSGA－II 算法（Improved Non－dominated Sorting Genetic Algorithms，INSGA－Ⅱ）求解該模型。修改擁擠度距離計算，增加種群分布性，增加外部存檔對全局非支配解進行存儲，保留解的多樣性，并通過K－means 聚類方法對外部存檔進行聚類操作，從而有效地提高了算法的性能。 INSGA－Ⅱ算法流程圖如圖2 所示。

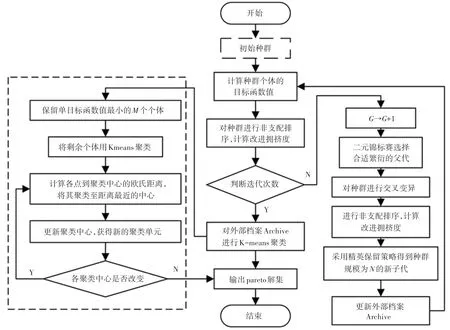
圖2 INSGA－Ⅱ算法流程圖Fig. 2 INSGA－II algorithms flow chart

3.1 染色體編碼

根據軸輻式應急物資供需網絡模型的特點，對其進行編碼設計。 一條染色體由3 個子串組成，每條染色體表示一個可行解。 子串1 采用實數編碼，長度為i?j，表示供需網絡中供應點i向需求點j的實際物資供給情況；子串2 采用0－1 整數編碼，長度為i?j，代表供需網絡各路徑的轉運／直達判別，1 代表轉運，0 代表直達；子串3 采用實數編碼，長度為i＋j，表示供應點i和需求點j被分配給樞紐點k的情況；染色體的總長度為2?i?j＋i＋j，示意如圖3 所示。

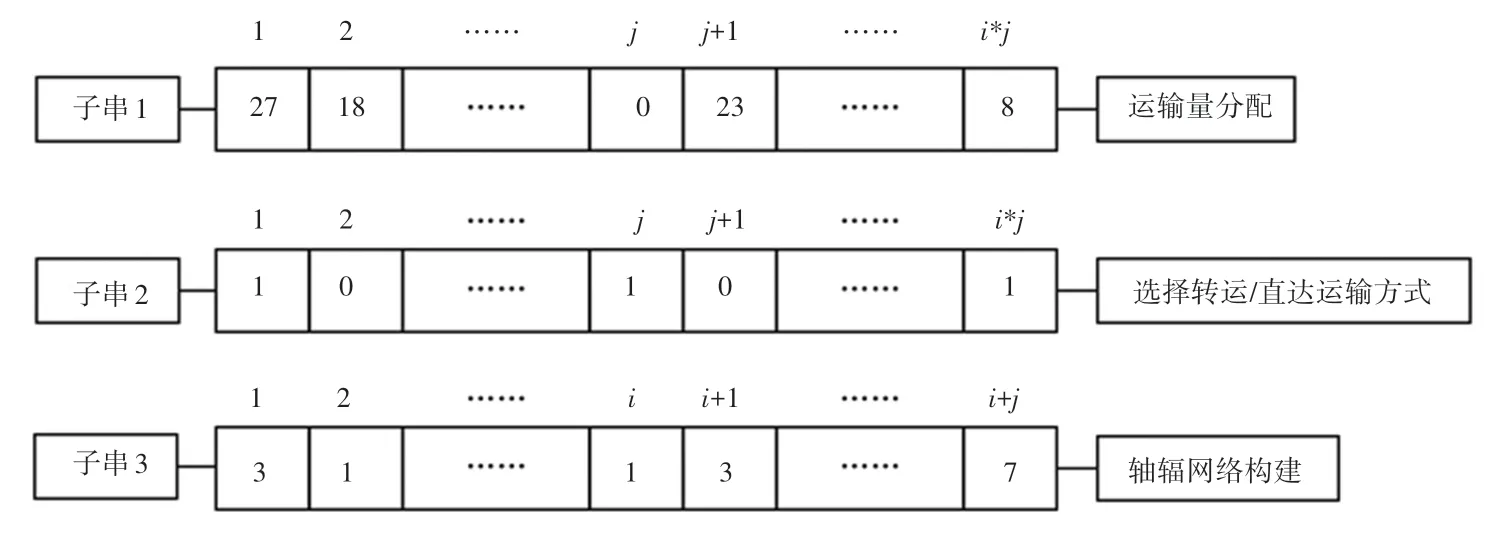
圖3 染色體編碼示意圖Fig. 3 Schematic diagram of chromosome coding

3.2 改進擁擠度距離

傳統擁擠度距離計算方法可以使得種群呈現均勻性，但是對于目標函數差異性較大的個體不易獲得遺傳下去的機會，從而不利于種群的分布性。 因此，構建擁擠度距離方差公式，如式（29）所示：

其中，代表第i＋1 個個體在第m個目標函數的值，代表與第i＋1 個個體相鄰的第i －1 個個體在第m個目標函數的值。

3.3 添加外部存檔

在每一次迭代結束后都會產生一組新的非支配解，因此，添加外部存檔將當前種群中所有標記為非支配的個體進行存儲，從而將全局的非支配解進行保存，使得其更逼近真實的帕累托前沿。 對于外部存檔的更新規則如下：

（1）將當前種群中所有標記為非支配的個體添加到外部存檔中進行存儲，這些個體是當前種群中的非支配解；

（2）對外部存檔進行去重操作，確保其中不包含重復的個體；

（3）對外部存檔中的所有個體進行非支配排序，將其分為不同的層次；

（4）從所有非支配層中選出最好的一層，作為新的非支配解集。 這個過程中，只有標記為非支配的個體才會被保留，其他個體都將被刪除。

3.4 K－means 聚類全局非支配解集

外部存檔存儲了全局的非支配解，其存儲的非支配解過于龐大，K－means 是經典的數據聚類算法［15］。 本文使用K－means 聚類對外部存檔進行選擇，該操作的步驟如下：

（1）從外部存檔中提取出所有個體的目標函數值，并將其歸一化到［0，1］的范圍內，在保留3 個目標函數分別最大的3 個解以外，隨機從剩下的解集中選擇97 個解，每個解代表一個聚類中心Ci；

（2）對于剩下的每個解，根據解xj與聚類中心Ci的歐氏距離，將每個解分配到與其最相似的聚類中，該距離計算公式如式（30）所示：

其中，m為空間維度，本文每個解有3 個目標函數，因此m＝3。

（3）計算每個聚類的新中心；

（4）迭代步驟2 和步驟3，直到目標收斂；

（5）在每個聚類中找到最靠近質心的解，并使其成為該聚類的代表解，并將解集輸出。

4 算例分析

4.1 案例背景與參數設置

傳染病疫情爆發初期，各市應急醫療物資嚴重短缺，全國各地的物資在政府的統籌調度下前往湖北省各疫區。 本文以湖北省12 個市級作為需求點，選取北京南站、上海虹橋站、成都東站、西安北站、鄭州火車站、南京火車站、重慶北站、杭州東站這8 個國內規模較大設施完善的火車站作為備選樞紐點，并將其編號為1～8。 根據疫區范圍及地理位置，選取9 個國家應急物資儲備庫作為應急物資供應點。各兩地之間的行駛距離通過百度地圖進行查詢。 評價指標體系中各數據通過湖北省統計局2020 統計年鑒（http：／ ／tjj.hubei.gov.cn／）和湖北省衛生健康委員會（http：／ ／wjw.hubei.gov.cn／）獲得，評價指標體系中各級指標數據見表2；物資需求點的防疫物資口罩的需求量依據易感人群2 個／人／天，感染患者依據專家建議4 小時需更換一次口罩，設定為6 個／人／天的配比預估需求量，湖北省各市需求量見表3；依據各物資儲備庫規模預估現階段應急物資庫存量見表4；按照需求點應急物資緊迫度評價指標計算得出各需求點的需求緊迫度見表5，并根據緊迫度評價結果對物資最低滿足量進行分級，I、II、III 級的物資最低滿足量分別為0.7、0.6、0.5。 根據中國人民共和國國家發展改革委（https：／ ／www.ndrc.gov.cn／）中的國家鐵路貨物統一運價，將本文鐵路運輸成本定為0.115 元／tkm；根據公路運輸價格相關規定及各公路運輸公司定價數據，本文將公路運輸成本設定為0.45 元／tkm。 定義公路運輸速度60 km／h，鐵路運輸速度100 km／h，樞紐點選擇數量為5 個，需求點能接受的最晚到達時間RTj為24 h，干線折扣率αkm為0.6。

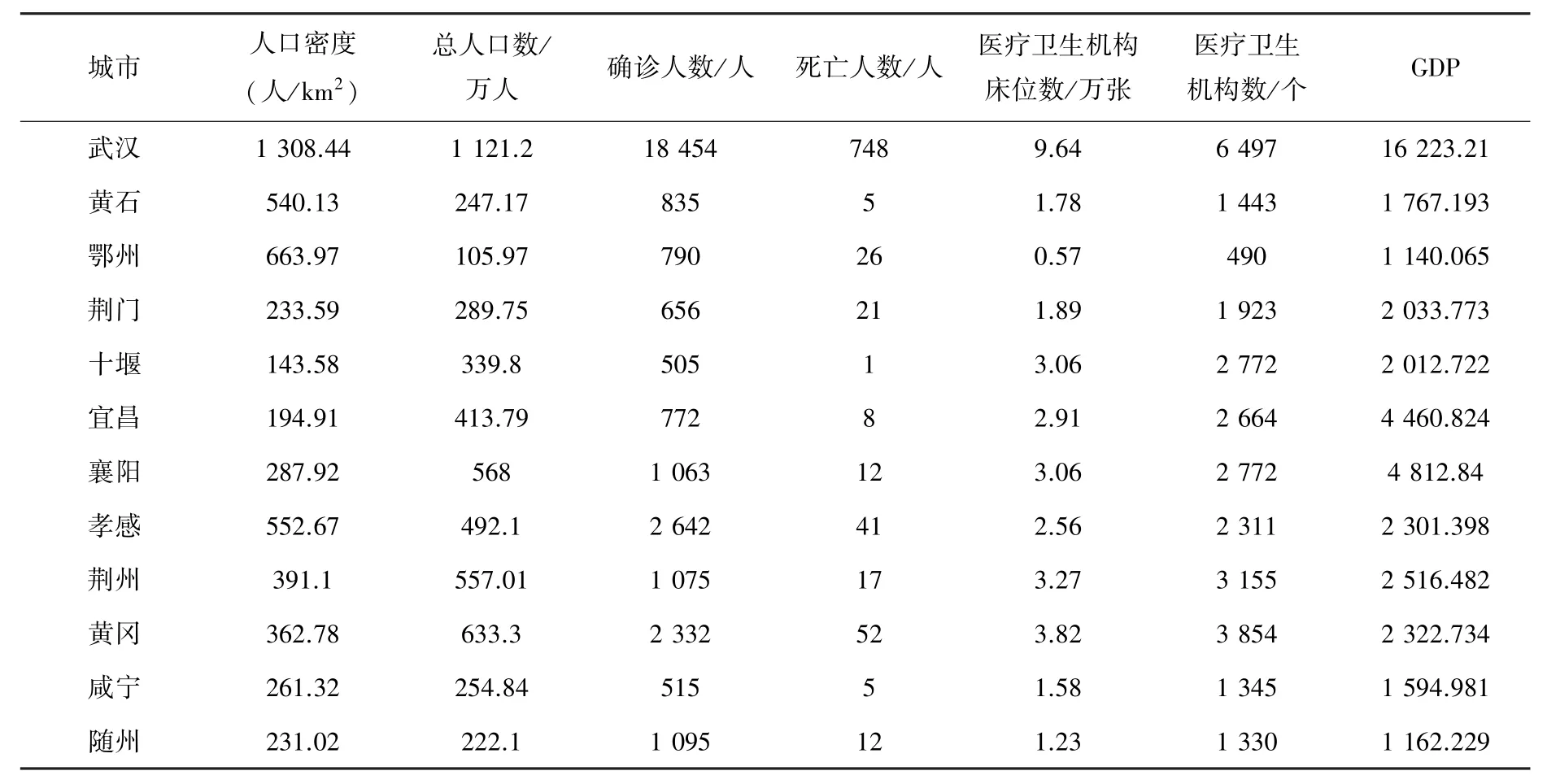
表2 評價指標體系各級指標數據Tab. 2 Data of indicators at all levels of the evaluation index system

表3 需求點物資需求量Tab. 3 Material requirements of different regions

表4 供應點物資庫存量Tab. 4 Material storage of different regions

表5 需求點的需求緊迫度Tab. 5 Urgency of different regions

INSGA－II 算法的參數設置：種群規模popsize＝100，最大迭代次數maxgen＝2 000，交叉概率pc＝0.8，變異概率pm＝0.1。

4.2 算法對比

通過將NSGA－II 算法與INSGA－II 算法各自獨立運行10 次，結果均能得到帕累托前沿解集，為了進一步評價算法的性能，引入評價指標Spacing ，Spacing 是衡量算法解集分布性的指標，其值越小，表明算法越好， 兩個算法各自獨立運行10 次，算法性能Spacing 指標箱型圖結果如圖4 所示。 INSGAII 算法的平均值低于NSGA－II 算法，表明INSGA－II算法在求解本文模型的帕累托前沿解集在解空間內具有更好的分布性和延展性；其次INSGA－II 算法的箱體比NSGA－II 算法要窄，這表明INSGA－II 算法具有更好的穩定性。

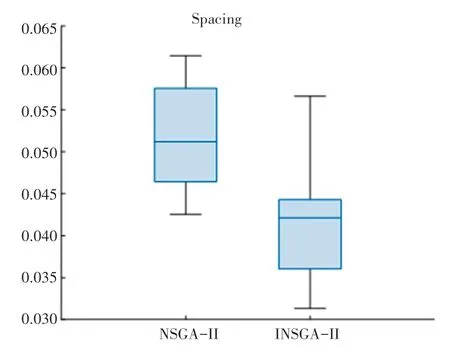
圖4 算法性能Spacing 指標箱型圖Fig. 4 Box plot of Spacing metrics algorithm perform

4.3 結果分析

本模型的運算結果如圖5 INSGA－II 的帕累托前沿解集所示。 其中，3 個維度的坐標分別表示物資分配公平性F1、物資運輸有效性F2、系統總成本F3。 由于目標之間存在一定的沖突性，最終方案的抉擇取決于決策者的偏好。 例如：在突發事件初期，更低的物資缺口是主要考慮的因素，可以選擇目標函數1 在帕累托前沿上表現最好的方案；在突發事件中后期，相關單位對疫情防控有了一定的把控時，期望在經濟性上有更好的體現，可以選擇目標函數3 在帕累托前沿上表現最好的方案。 圖5 中的點需求缺口最小、點時間延誤最小、點系統總成本最小這3 個點分別為3 個目標各自最優時的方案。 決策者也可以為目標函數賦權，從而得到一個綜合性的解，由于前期低缺口的重要程度較高，可以接受一定的時間延誤，以及弱經濟性原則，從而將權重設定為1／2、3／10、2／10，得到綜合性賦權方案，并將這4 個方案標注在圖5 上。 這4 個方案的3 個目標函數值見表6。

表6 4 個方案的目標函數值Tab. 6 Objective functions of the four programs

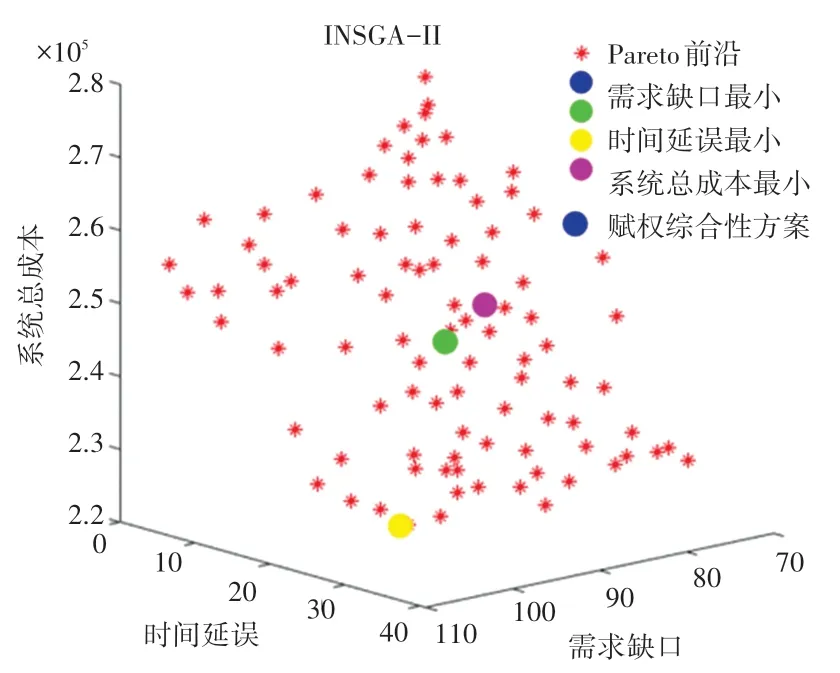
圖5 INSGA－II 的帕累托前沿解集Fig. 5 INSGA－II Pareto frontier solution set

這4 種方案代表不同的決策偏好，一個目標函數的提升，會犧牲其他目標函數，因此在實際決策過程中，可以根據現實情況對這3 個目標函數的偏好從帕累托解中選擇合適的方案。 賦權綜合性方案的調度，需求點的物資實際分配數量見表7，運輸方式見表8。 通過表7，表8 可以直觀看到所有物資的運輸路徑，如北京供應點向武漢需求點從樞紐點1 北京南站和樞紐點5 通過公鐵聯運向鄭州站運輸物資38 t，南寧供應點向武漢需求點通過公路直達運輸物資11 t。

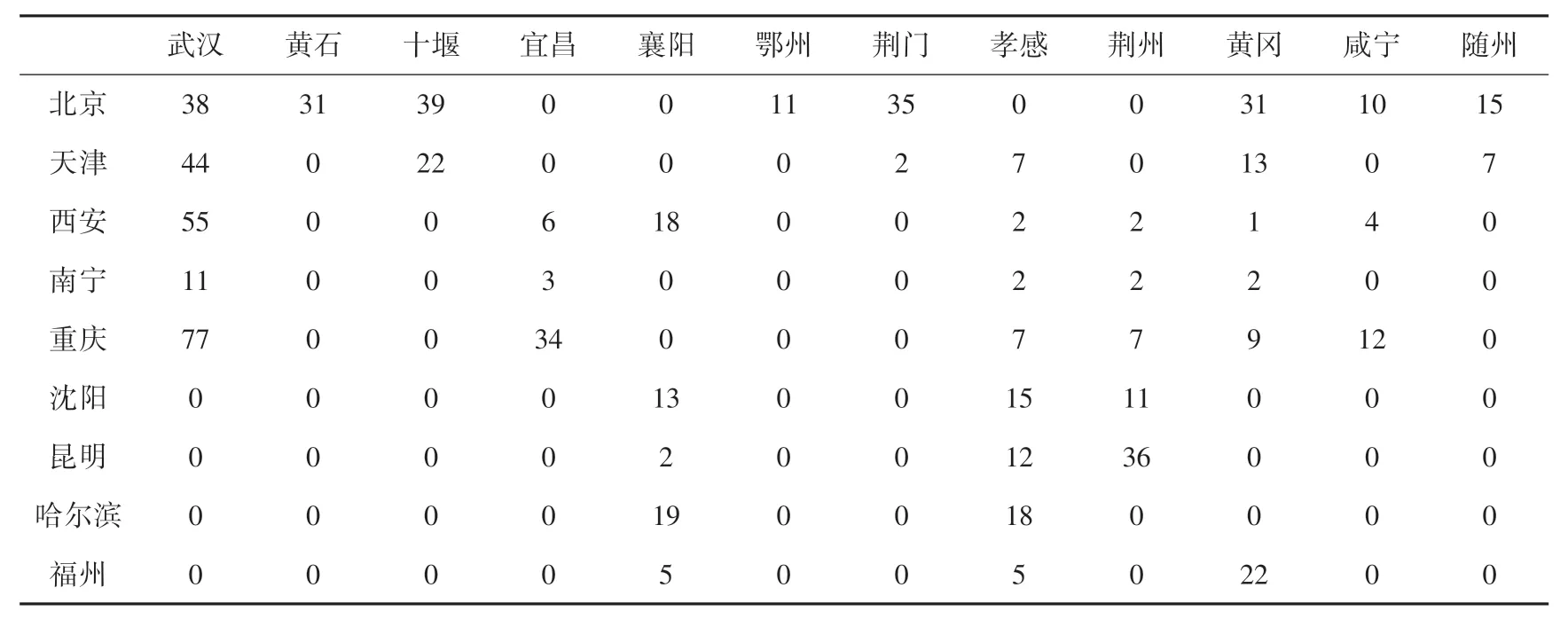
表7 需求點的物資實際分配數量（t）Tab. 7 Actual quantity of materials allocated at the point of demand （tons）

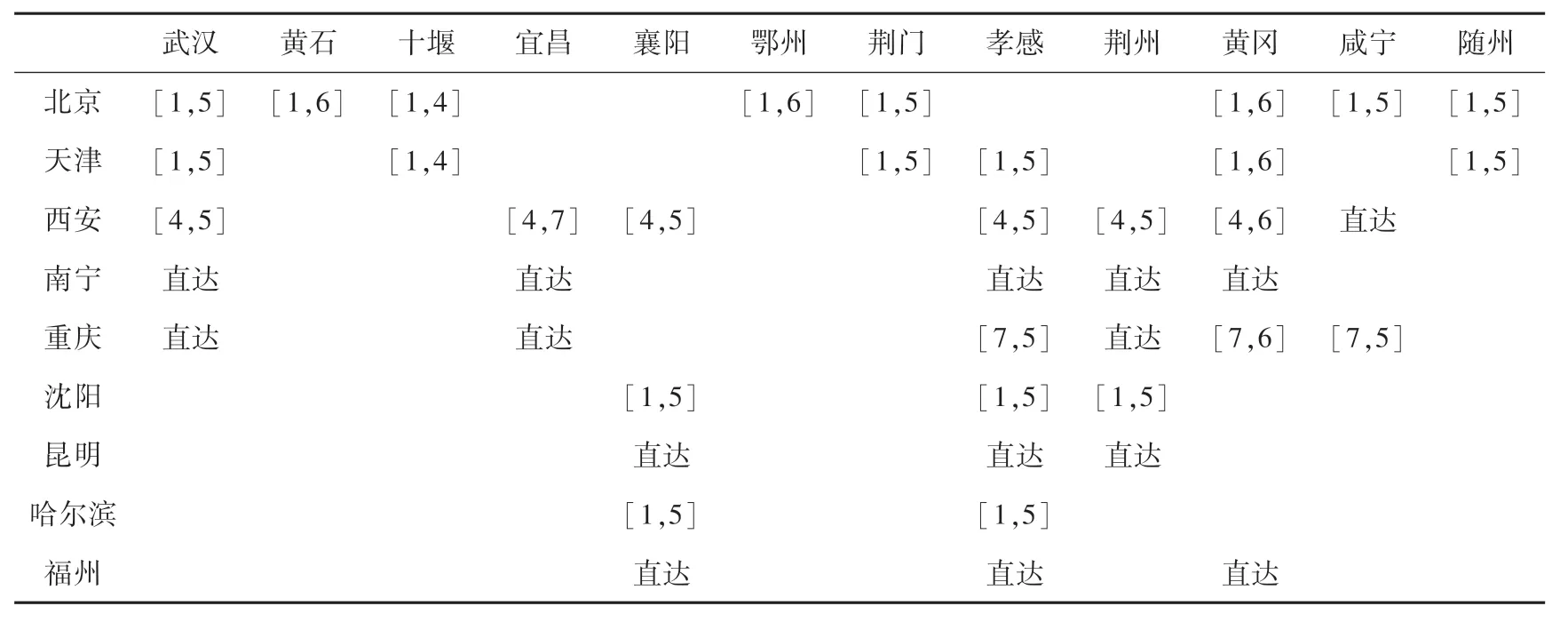
表8 應急物資調度方案的運輸方式Tab. 8 Transportation mode of material dispatch program

為進一步驗證模型對公平性的有效性，模擬不考慮緊迫度和不考慮軸輻網絡的模型，使用INSGA－II 算法對兩個模型求解，本文選取兩個模型中的相同權重下的綜合賦權方案進行對比，方案A 表示本文考慮緊迫度和采用軸輻網絡模型的方案，方案B表示不考慮緊迫度和不考慮軸輻網絡模型的方案。方案A 的物資滿足率如圖6 所示，方案B 的物資滿足率如圖7 所示，方案間的時間延誤對比如圖8 所示，方案間的成本對比如圖9 所示。

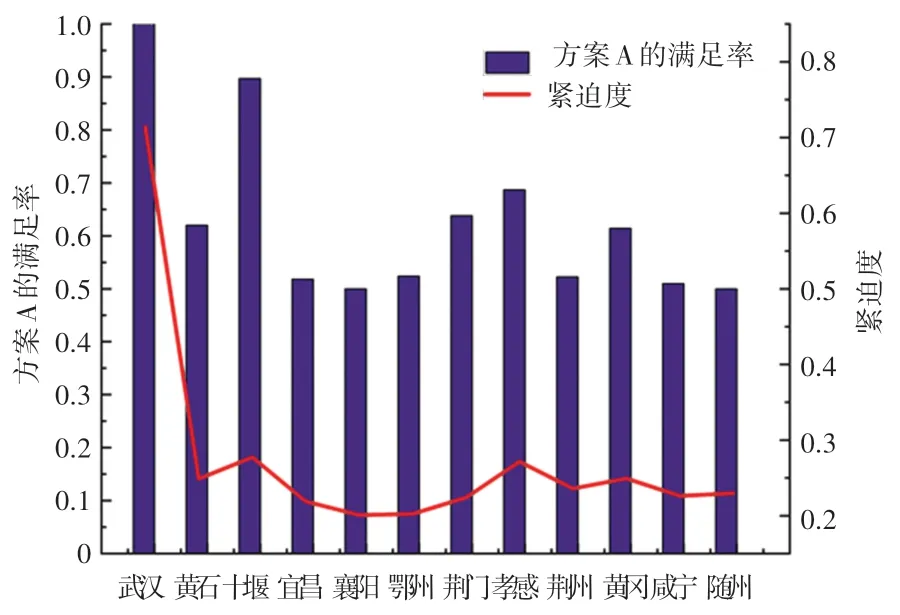
圖6 方案A 的物資滿足率Fig. 6 Material satisfaction rate for program A

圖7 方案B 的物資滿足率Fig. 7 Material satisfaction rate of program B

圖8 方案間的時間延誤對比Fig. 8 Comparison of time delays between programs

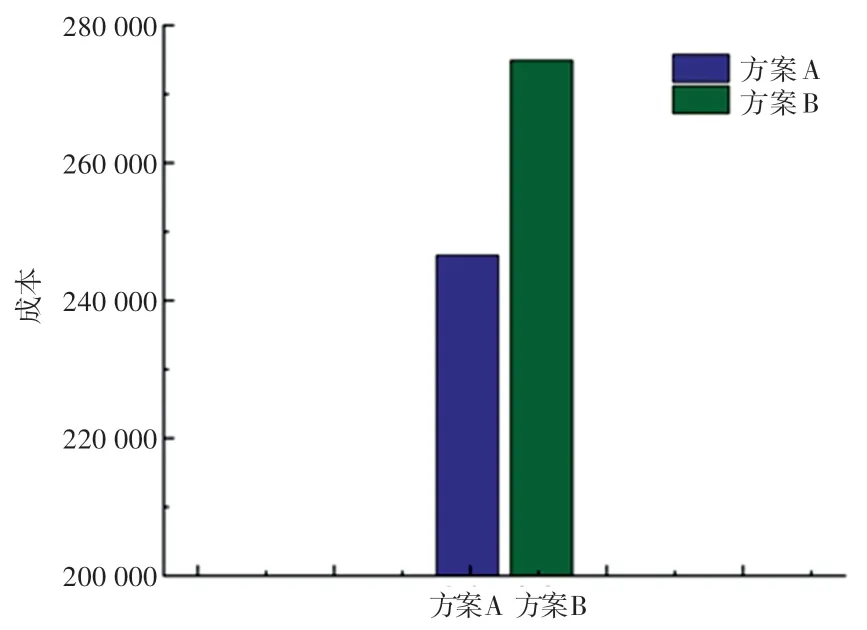
圖9 方案間的成本對比Fig. 9 Comparison of time cost between programs

由圖6－圖9 可知：本文得出的方案（方案A）考慮緊迫度，其對物資分配的公平性大于不考慮的方案（方案B），其時間延誤和成本也小于方案B，這表明本文構建的考慮緊迫度的軸輻應急物資供需網絡是可行的。 在方案B 中，物資滿足率最高的城市是十堰、襄陽和隨州，這3 個城市的物資滿足率在98%～100%，基本完全滿足需求，而疫情最嚴重的武漢物資滿足率僅有65%，對于突發公共衛生事件的應急物資分配而言是不合理的。 而在方案A 中，作為緊迫度最高的城市武漢，獲得了所有需求點中最高的物資滿足率100%，這是因為本模型通過衡量需求點間的差異性，使得優先對最緊迫的城市進行物資分配，從而保障了緊迫度高的城市的物資充足供給。 其次，從時間延誤和成本的角度來看，方案A的表現均比方案B 好，是因為軸輻網絡通過選擇時間更短成本更低的軸點間鐵路運輸，有效地提升了調度效率。

5 結束語

本文針對突發公共衛生事件下的應急物資調度問題，構建了考慮需求緊迫度的以需求缺口最小、時間延誤最少和系統總成本最小為目標的應急物資軸輻供需網絡優化模型。 首先，結合應急物資調度的特點，構建需求緊迫度評價指標體系，并使用熵值－TOPSIS 法對需求點緊迫度進行求解；其次，基于軸輻結構在軸點間的規模運輸能力，對傳統調度供需網絡進行改進，提出基于軸輻結構多式聯運的應急物資供需網絡模型；最后，基于模型設計改進的NSGA－II 算法，INSGA－II 算法對擁擠度進行改進，添加外部存檔對全局非支配解進行存儲，并對外部存檔進行K－means 算法聚類。 通過對實例的結果分析，發現模型可以求解出有效的帕累托前沿解集，并相比于不考慮緊迫度和不考慮軸輻結構的模型，本模型的物資調度具有更好的公平性，并在時間延誤和成本上更優。 為了更貼近實際應急物資調度情況，后續研究將進一步考慮軸點的容量限制，同時考慮多品類應急物資、多階段的動態調度。