考慮失穩模態型初始缺陷船體艙段極限強度分析

張宜杰，李淇雯，邱國志，夏利娟

(1.上海交通大學 船舶海洋與建筑工程學院，上海 200240；2.上海市公共建筑和基礎設施數字化運維重點實驗室，上海 200240)

0 引言

傳統規范采用許用應力法校核船體梁總縱強度，該方法具有計算簡便、快捷的特點[1]。但許用應力法僅采用一個安全系數K確定結構的可靠程度，不能反映船體的實際承載能力。而建筑鋼結構設計標準經歷了許用應力法和以概率為基礎的極限狀態設計法階段，進入以非線性分析計算極限強度為基礎的高等分析法階段[2]。高等分析法是考慮結構缺陷直接計算極限強度的設計方法，鐘毅等[3–5]針對船體構件加筋板極限強度計算方法展開研究，但針對艙段或全船整體結構極限強度的計算方法研究較少。隨著計算機計算能力的增強，基于艙段結構甚至全船結構的高等分析法進行船舶結構設計成為發展趨勢。

相關研究[6–9]表明，高等分析法中所引入的初始缺陷形態至關重要，直接影響極限強度計算結果。船舶結構中存在凹陷、初始變形和殘余應力等多種初始缺陷[10]，現階段一般通過施加結構整體位移缺陷來模擬結構中存在的各種缺陷形式。目前，常采用屈曲型初始撓度引入初始缺陷進行艙段極限強度計算。白寶強[11]應用Abaqus 軟件對一艘集裝箱船艙段引入屈曲型初始缺陷的極限強度進行了研究；高本國等[12]應用Marc 軟件對船體梁引入屈曲型初始缺陷的極限強度進行了研究；劉明瑞[13]通過引入屈曲型初始缺陷研究了加筋板及箱型梁的極限強度。然而屈曲型初始缺陷往往只能體現結構的局部缺陷，尤其針對艙段結構而言，這種現象更加明顯，難以體現艙段結構的整體缺陷分布，按這種初始缺陷引入方式不能準確獲得艙段極限強度。

本文借鑒建筑鋼結構中一致缺陷模態法[14]，針對艙段極限強度計算，提出一種新的失穩模態型初始缺陷引入方法。失穩模態型初始缺陷能模擬艙段結構的整體位移缺陷，綜合考慮結構中其他可能存在的缺陷，確定最大缺陷值，按此方法引入初始缺陷后，能較準確計算艙段結構極限強度。借助有限元軟件Ansys，通過對比失穩模態型初始缺陷與同等最大缺陷值下屈曲型初始缺陷的艙段極限強度計算結果，論證失穩模態型初始缺陷引入方法的適用性。基于失穩模態型初始缺陷形態下船體艙段和局部加筋板達到極限強度的變形和應力分布結果，指出艙段結構模型優化時的關鍵部位，并給出相應的優化建議。該研究可完善船舶結構高等分析法中初始缺陷的計算方法，促進高等分析法在船舶結構設計中的推廣應用。

1 船體艙段分析計算模型

參考某挖泥船構造形式，提取關鍵構件建立艙段有限元模型。艙段沿船長方向為X軸，沿加強筋方向為Y軸，沿豎向為Z軸。甲板及艙壁均采用加筋板，為了與Tanaka 系列加筋板[15]試驗結果進行極限強度計算結果對比，加筋板幾何參數均選自Tanaka 系列加筋板試驗。加筋板厚度t=5.65 mm，加強筋高度hw=110 mm，加強筋厚度tw=10.15 mm，加強筋間距d=360 mm，強橫梁間距dx=1 080 mm。強橫梁截面為T型鋼，腹板高度hTf=700 mm，腹板厚度tTf=16 mm，翼緣寬bTw=200 mm，翼緣厚tTw=20 mm。加筋板及強橫梁橫截面如圖1 所示。艙段沿X向布置9 道強橫梁（包括兩端），艙段起始X坐標為0，終止X坐標Xend=8dx=86 400 mm。上層甲板沿Y方向最大跨度L=16 800 mm。采用Ansys 建立艙段結構幾何模型，單元類型為shell181，網格尺寸為60 mm×60 mm，單元類型為shell181。全艙段材料假定為理想彈塑性，忽略材料的應力強化作用，材料極限強度σy=315 MPa，彈性模量E=2.058×105MPa，泊松比ν=0.3，材料的屈服準則為von Mises 屈服準則。最終艙段整體結構模型如圖2 所示。

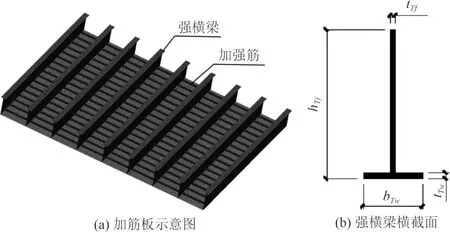
圖1 加筋板及強橫梁示意圖Fig.1 Schematic diagram of stiffened plate and strong beam

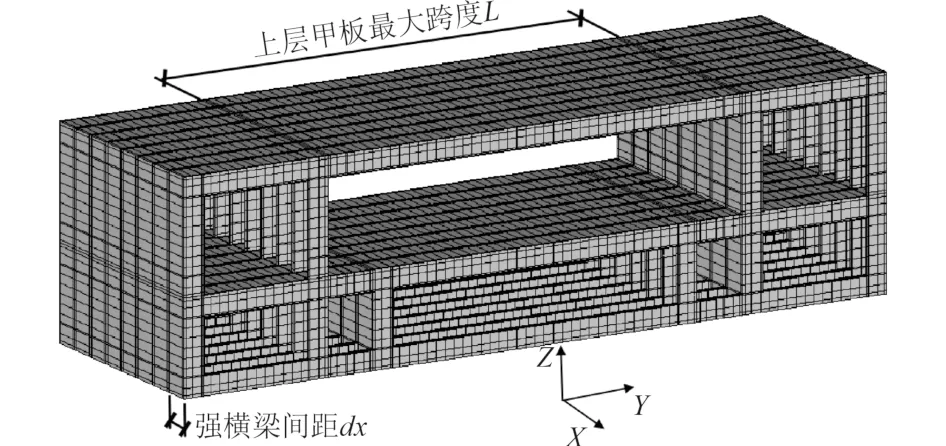
圖2 艙段整體結構模型Fig.2 Overall structure model of cabin section

根據模型荷載和約束條件[11]，荷載只考慮純彎作用，在艙段兩端截面施加彎矩；約束考慮艙段連續性條件并限制剛體位移。具體荷載及約束條件如下：

1）艙段兩端截面（X=0，X=Xend）分別施加Y向正彎矩和負彎矩，彎矩值相同。忽略加強筋的影響，通過對艙段截面上施加沿Z 向線性分布的正應力模擬彎矩作用。取艙段上甲板壓應力峰值與加筋板單軸壓縮極限強度[15]進行對比；

2）艙段兩端截面的甲板與底板約束Y向轉動，考慮艙段連續性條件；

3）艙段中間截面（X=Xend/2）所有節點約束X向位移及Y軸轉動，對稱軸上部點約束Y向位移，對稱軸下部點約束Y向和Z向位移，以限制剛體位移。

2 屈曲型初始缺陷艙段極限強度計算

2.1 屈曲型初始缺陷極限強度計算過程

采用屈曲型初始缺陷進行艙段極限強度計算，需要通過艙段結構的低階屈曲模態或疊加后的屈曲模態建立初始撓度引入理想結構，再進行非線性分析。具體實現過程為：

1）對艙段理想模型進行線性特征值分析，得到理想結構的多階屈曲模態；

2）選取合理的特征值屈曲模態作為初始缺陷形態，按最大缺陷值為Dmax引入至理想模型，得到考慮初始缺陷后的屈曲型初始缺陷模型；

3）對該模型進行非線性分析，得到帶屈曲型初始缺陷的艙段結構極限強度 σa。

2.2 屈曲型初始缺陷極限強度計算結果

屈曲型初始缺陷極限強度計算結果依賴于最大缺陷值Dmax的取值。一般取Dmax為艙段跨度L的1/400[16]。但考慮到特征值屈曲模態可能為局部屈曲，將最大缺陷值Dmax取為強橫梁間距dx的1/400 進行計算對比。研究表明[17]，當計算對象為局部加筋板時，取Dmax為dx/400=2.7 mm計算所得極限強度結果為σa,l=251.5 MPa，與試驗結果較為接近。但計算對象為艙段整體模型時，屈曲型初始缺陷引入方法的適用性有待論證。

取圖3 所示的艙段結構第1 階模態作為初始缺陷模態，對比這2 種Dmax取值方式下艙段結構極限強度σa與Tanaka系列加筋板試驗極限強度結果σ0=249.9 MPa的差異，如表1 所示。結果表明：

表1 屈曲型初始缺陷極限強度結果Tab.1 Ultimate strength results of buckling mode initial deflection

圖3 第1 階屈曲型初始缺陷形態Fig.3 Initial deflection form of first order buckling mode

1）當Dmax按艙段跨度計算時，計算結果明顯偏小，與試驗結果相差–8.36%。這是因為第1 階屈曲型初始缺陷為局部缺陷，局部失穩區域內節點初始缺陷被過度放大，導致最終極限強度結果偏小。

2）當Dmax按強橫梁間距計算時，計算結果明顯偏大，與試驗結果相差12.85%，與局部加筋板計算結果相差12.13%。這是因為初始缺陷較明顯的區域（見圖3峰值區域）占整個甲板的比例很小。在非線性分析過程中，當峰值區域進入塑性狀態后，由附近的甲板和艙壁分擔部分荷載，最終極限強度結果比試驗結果偏大。

因此第1 階屈曲型初始缺陷無法反映艙段整體缺陷。為探討能否選取到合適階數的屈曲模態進行艙段結構極限強度計算，再次對艙段結構模型進行線性特征值分析，計算得到的前100 階屈曲模態均為局部屈曲，典型屈曲模態如圖4 所示。挑選屈曲區域范圍較大的第90 階模態作為初始缺陷模態，Dmax按強橫梁間距的1/400 進行艙段極限強度計算，計算結果為290.0 MPa，仍顯著偏大，與試驗結果相差16.05%。因此，對于艙段整體結構，很難取到合適的屈曲型初始缺陷形態。

圖4 艙段典型屈曲模態（m 為屈曲模態階數）Fig.4 Typical buckling mode of cabin section(m is the order of buckling mode)

3 失穩模態型初始缺陷艙段極限強度計算

3.1 失穩模態型初始缺陷極限強度計算過程

由于屈曲型初始缺陷引入方法對艙段結構并不適用，借鑒空間網殼結構中一致缺陷模態法，提出一種適用于艙段極限強度計算的初始缺陷引入方法。考慮失穩模態型初始缺陷極限強度計算具體過程為：

1）對艙段理想模型進行非線性分析；

2）選取理想模型在極限強度下的失穩模態作為初始缺陷形態，按最大缺陷值為Dmax引入至理想模型，得到艙段考慮初始缺陷后的失穩模態型初始缺陷模型；

3）對該模型進行非線性分析，得到帶失穩模態型初始缺陷的艙段結構極限強度 σb。

上述最大缺陷值Dmax取艙段跨度L的1/400 進行艙段極限強度計算。

3.2 失穩模態型初始缺陷極限強度計算結果

應用失穩模態型初始缺陷引入方法，取Dmax為強橫梁間距dx的1/400 計算局部加筋板的極限強度，結果為σb,l=245.7 MPa[17]。而當計算對象為艙段整體結構時，取Dmax為艙段跨度L的1/400，引入圖5 所示的失穩模態型初始缺陷進行極限強度計算，結果為σb=247.1 MPa。結果表明，失穩模態型初始缺陷艙段極限強度結果與試驗結果一致，相差僅1.12%。這是因為理想艙段結構的失穩模態表現為結構整體變形形態，失穩模態型初始缺陷引入方法對艙段整體結構和局部加筋板極限強度計算均適用。因此，失穩模態型初始缺陷可用于船舶結構高等分析法的初始缺陷取值方法。

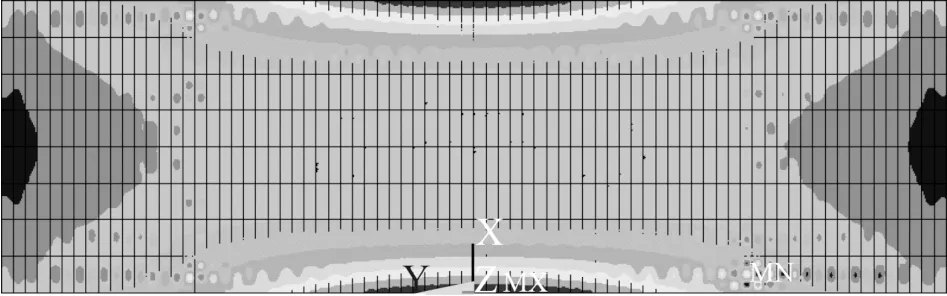
圖5 失穩模態型初始缺陷形態Fig.5 Initial deflection form of instability mode

3.3 變形及應力分布結果

采用失穩模態型初始缺陷計算所得艙段結構在極限強度下Z向變形及von Mises 應力分布如圖6 所示。可知：

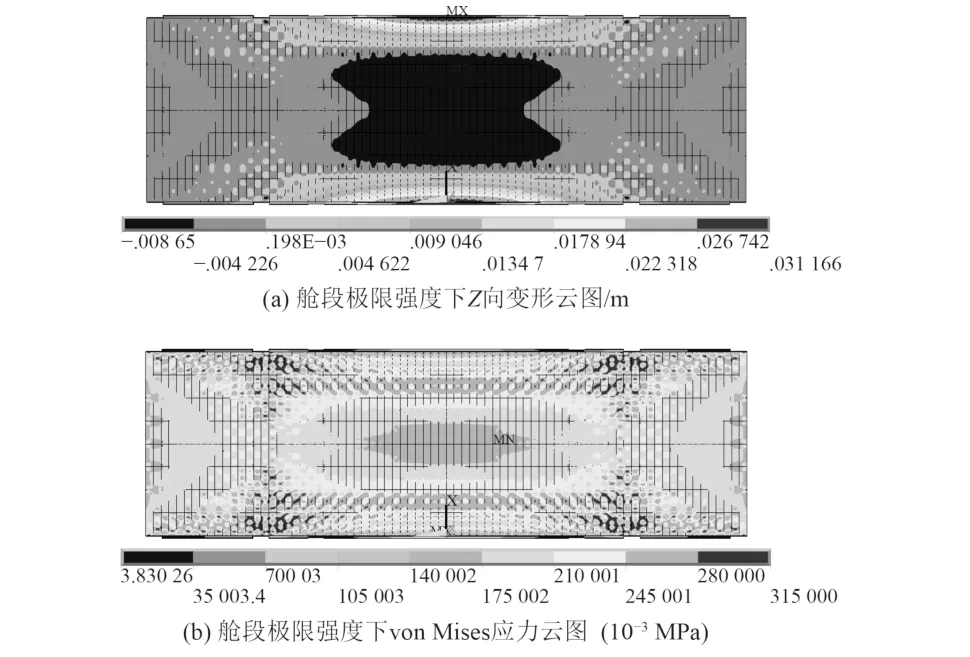
圖6 艙段極限強度下變形和應力分布Fig.6 Deformation and stress distribution under ultimate strength of cabin section

1）艙段最大豎向變形為0.031 m，發生在上層甲板兩端的跨中位置，上甲板兩端發生翹曲，整體變形與失穩模態型初始缺陷形態基本一致；

2）艙段上甲板應力分布不均勻，與中間兩艙壁交界處應力較大，而板中區域和靠近舷側區域應力較小。

局部加筋板在極限強度下von Mises 應力分布較為均勻[17]，而艙段甲板應力分布明顯不均勻。這是因為艙壁等其他船體構件對甲板應力分布存在影響，局部加筋板的分析結果不能反映整個甲板的應力狀態。若僅依據局部加筋板極限強度結果進行甲板優化設計，會因無法準確考慮甲板受力不均勻的實際情況而導致材料浪費，優化空間有限。

4 結語

本文提出一種針對艙段極限強度計算的失穩模態型初始缺陷引入方法，通過對比采用失穩模態型初始缺陷與屈曲型初始缺陷的艙段極限強度計算結果，并結合試驗結果，論證所提方法的適用性，并分析了艙段達到極限強度時的變形和應力分布。主要研究結論如下：

1）艙段的屈曲失穩模態大多表現為局部屈曲，最大缺陷值難以選取，基于艙段跨度計算最大缺陷值時，所得艙段極限強度相對試驗結果偏低8.36%；基于加筋板支撐（強橫梁）間距計算最大缺陷值時，所得艙段極限強度相對試驗結果偏高12.85%。因此，屈曲型初始缺陷引入方法不適用于艙段結構的極限強度計算。

2）理想艙段結構的失穩模態表現為結構整體變形形態，失穩模態型初始缺陷計算所得艙段極限強度與試驗結果相差僅1.12%，能準確預測艙段結構極限承載能力。因此，失穩模態型初始缺陷引入方法更適用于艙段結構極限強度計算及船體結構高等分析法的初始缺陷取值。

3）艙段整體結構在極限強度下應力分布不均勻。建議考慮甲板受力不均勻的實際情況對艙段進行優化設計，對艙段甲板與艙壁交界區域應適當加強，對甲板板中區域和靠近舷側區域部位適當削弱。