起伏管氣液兩相攜液能力的試驗研究*

徐龍宇 張慢來, 夏齊 汪國威 廖銳全

(1. 長江大學機械工程學院 2. 中國石油天然氣集團有限公司采油采氣重點實驗室長江大學分室)

0 引 言

隨著我國石油天然氣工業的發展, 氣田集輸管線分布越來越廣, 其中, 濕氣輸送工藝以其流程簡單高效的特點, 現階段已成為氣田集輸管線的主要形式。 對于地勢起伏變化的地面管線, 濕氣極易形成積液, 當氣量較小時, 積液增加, 明顯減小氣體的過流面積, 導致管線壓降增大, 甚至影響管線的正常輸送[1-4]。 因此, 開展起伏管氣液兩相攜液能力研究具有重要意義。

D.H.BEGGS 等[5]通過理論推導得到考慮傾角的持液率計算關系式; H.MUKHERJEE 等[6]針對Beggs-Brill 半經驗式中的問題開展試驗研究并得到全部傾角范圍內的相關式; XIAO J.J.等[7]針對不同的流型建立動量、 質量方程, 得到對應的持液率計算式。 國內外學者建立了傾斜管和起伏管氣液兩相的機理模型[8]。 A.S.KAYA 等[9]采用 Ansari 等的方法建立了微傾管的機理模型; A.R.HASAN等[10]基于漂移模型提出簡易的兩相流機理模型。王琦[11]開展水平氣液兩相流的模擬試驗, 按垂直段、 水平段、 傾斜段等不同管段研究攜液參數, 得出傾斜段具有相對而言最差的攜液能力; SHI J.T.等[12]對傾斜管線的氣液兩相的攜液機理進行研究,觀測了不同傾斜角下的氣液形成的液滴的直徑及形狀變化。 對于起伏管的數學動力模型也相對較少,對起伏管的動力模型做出了相關的調研。S.L.SCOTT 等[13]建立起伏管段塞流模型, 研究發現在起伏管段內, 液塞長度會發生較大變化;Y.TAITEL 等[14]建立了可以跟蹤起伏管每個液塞的水動力學模型; 而SHARMA[15]則基于上述模型,建立了起伏管的段塞流跟蹤模型, 這個模型能夠準確預測管線中的進口壓力。

Y.TAITEL 等[16]通過研究大傾角下的地形起伏管線得出: 當起伏管傾角較大時, 可以忽略由氣液兩相摩擦引起的壓降損失, 認為壓降只受液彈重力的影響; 同時在此研究基礎上建立了針對兩相流起伏管線流動特性預測的數學模型和方程。 周良勝[17]利用 PIPEPHASE 軟件和新建立的持液率計算模型對幾種簡單地形起伏管段內持液率的變化情況進行模擬研究, 結果表明, 對于起伏較大的管線, 最低點與最高點間的高程差對平均持液率的影響最為明顯, 而管線傾角對其影響并不顯著。 梁法春[18]詳細分析了地形起伏濕天然氣集輸管線運行時的積液動態累積過程, 以及達平衡狀態時的臨界積液量, 對積液累計動態過程進行預測; 模擬結果表明, 對于高氣液比的某一固定管線, 設定其他條件不變時, 氣相流速對管內臨界積液量的影響顯著, 氣相攜液能力隨著氣體流速的增大而增強, 管內臨界積液量減小。

隨著流體力學的發展與研究的逐漸深入, 以及瞬態流理論的逐漸成熟, 國外許多石油公司開始開發能夠應用于井筒或管線的氣液兩相的數值模擬軟件。 現階段, 多相流數值模擬軟件分為: 穩態多相流和瞬態多相流數值模擬軟件, 且瞬態流的數值模擬遠比穩態流要復雜。 OLGA 為常見的一種瞬態多相流數值模擬軟件, 采用隱式算法來對壓力、 攜液量等參數進行運算求解, 更適合對起伏管線的氣液兩相流的模擬。 綜上所述, 現階段學者對起伏管路氣液流動規律的研究大多是停留在室內模擬試驗和流型判別與計算方法上, 而對傾斜管的流動規律方面的數值模擬較少。 筆者先運用室內模擬上傾管和下傾管的流動規律, 再運用仿真軟件對室內管線進行數值模擬并驗證數值模擬測試結果的準確性, 最后通過仿真軟件對起伏管線進行模擬研究, 對起伏管進行分段研究, 判斷上傾、 下傾和水平管積液的難易程度, 并將此方法用于集輸管線的測試中, 為集輸管線的安全運行提供理論基礎。

1 傾斜管室內試驗

傾斜管試驗在長江大學多相流試驗平臺進行,試驗裝置如圖1 所示。

圖1 傾斜管流動試驗裝置Fig.1 Experimental device of flow in undulating pipeline

本試驗選用自來水作為液相, 空氣作為氣相,用離心泵模擬地層產液, 水由離心泵增壓后經過氣相流量計、 氣液混合器進入試驗傾斜管; 空氣壓縮機模擬地層產氣, 空氣由空氣壓縮機加壓后經過氣相流量計、 氣液混合器進入試驗傾斜管; 氣液經氣液混合器流入試驗傾斜管, 最終由傾斜管的末端氣液分離, 空氣排向大氣, 液體排入儲水罐。

設置液體流量0 ～1 m3/h, 氣體流量20 ～80 m3/h; 整條管路采用透明有機玻璃管, 管線長度為13 m, 壓力測試段長度為7 m。 管線中段有高速攝像機, 檢測不同工況下管路流型變化; 并在管路3.8 和10.5 m 處設有壓力檢測設備, 通過電腦采集每秒的壓力數據; 管路末端設有計量秤, 檢測管路出液量。

1.1 試驗數據分析

由于試驗設備測量持液率不太方便, 所以此次試驗中測量攜液量來作為氣流攜液能力參數(持液率=進液量-攜液量)。 試驗通過記錄1 min 管線末端出液量來作為攜液量值, 得到上傾管的攜液量隨氣量變化, 如圖2 所示。 同理, 測量1 min 內管路3.8～10.5 m 處壓降變化值來衡量氣流攜液過程中能量變化, 如圖3 所示。

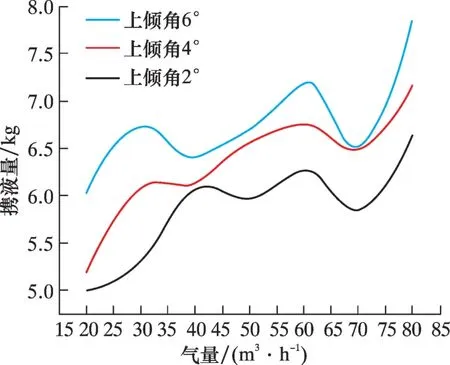
圖2 不同傾角的上傾斜管的攜液量Fig.2 Carrying capacity of the up-dip pipe with varied dip angles

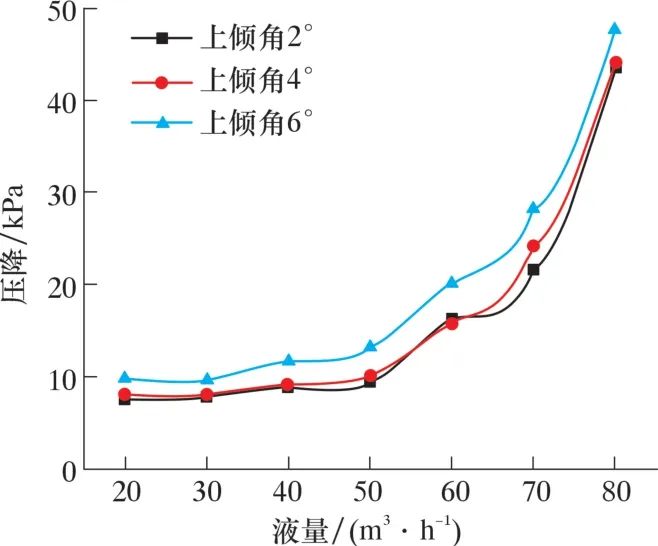
圖3 不同傾角的上傾斜管的壓降Fig.3 Pressure drop of the up-dip pipe with varied dip angles

由圖2 可以發現, 隨著氣量增大, 上傾管線攜液量逐漸增大, 且當氣量在35 ～70 m3/h 時攜液量波動較明顯。 這是因為此氣液比下, 管路中為段塞流, 段塞流為一種不穩定流動, 所以會呈現攜液量波動趨勢。 氣量35～70 m3/h 下的段塞隨時間推移移動的過程如圖4 所示。

由圖3 可以發現, 隨著氣量增大, 壓降逐漸增大。 這是由于在上傾管中氣液滑脫和氣體與管壁之間的滑脫損失較大, 大于重位壓力損失。 而前面整個起伏管線中壓降隨氣量增大逐漸減小, 因此造成壓力損失最大位置為凹陷管和凸起管處。

1.2 數值模擬可行性分析

運用仿真軟件模擬室內試驗的傾斜管, 本文選用黑油模型模擬氣液兩相流。 入口設置類型為Mass, 在此節點設置溫度和流量, 入口溫度設置為32 ℃, 入口氣量為20 ～80 m3/h, 入口液量為0.1～0.3 m3/h; 出口設置類型Pressure, 在節點設置出口壓力參數及流體數據, 出口壓力設置為1 MPa。 管線的參數設置: 管徑60 mm, 管線長度13 m, 表面粗糙度5 × 10-5m, 傳熱系數6.5 W/(m2·℃) , 模擬時間設置3 min。

圖5 所示為液量0.1 m3/h、 氣量20 ～80 m3/h下的olga 模擬攜液量與試驗值。 由圖5 可以看出,兩者非常接近, 攜液量隨著氣量的增大近似線性增加, 表明模擬攜液量的方法可行。

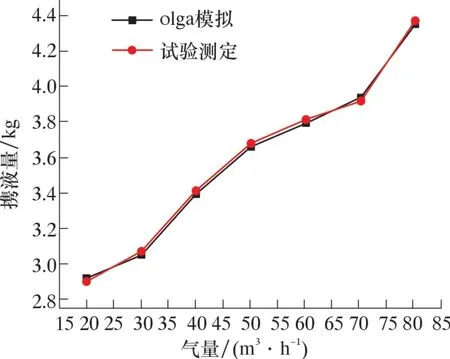
圖5 試驗測定與仿真模擬的數據對比Fig.5 Measured and simulated carrying capacity vs. gas flow rate

模擬的不同距離(3.8 和10.5 m) 處的壓差與試驗數據對比如表1 和圖6 所示。

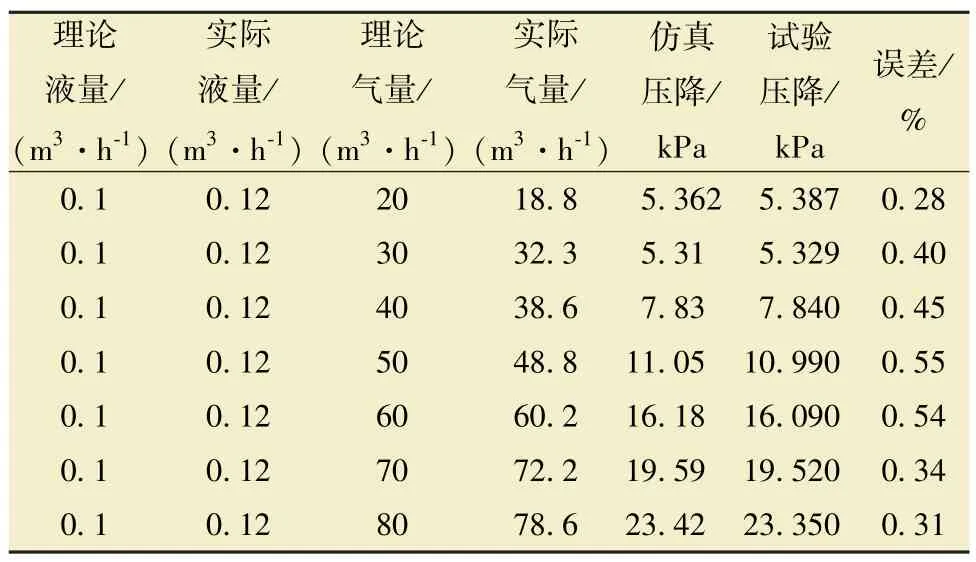
表1 壓降數據對比Table 1 Comparison of pressure drops

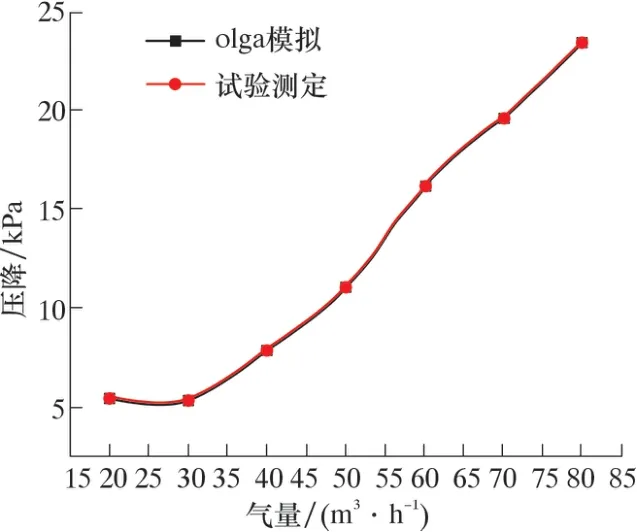
圖6 仿真數據與試驗模擬數據對比Fig.6 Measured and simulated pressure drop vs. gas flow rate

由圖6 和表1 可見, 壓降模擬值與實際數據接近, 誤差小于1%。 隨著氣量的增加, 壓降呈現快速增大趨勢。 當氣量為50 m3/h 時, 模擬值略小于試驗值, 當氣量大于50 m3/h 時, 模擬值偏大。

2 起伏管線的模擬研究

為研究起伏管線壓降和積液規律, 利用數值模擬軟件建立了數學模擬和幾何模型, 分析氣液量和傾角對起伏管線的壓降和攜液量變化規律的影響。

2.1 數學模型選擇

對于氣液兩相管線而言, 為了分析氣液兩相的流動規律, 需要在研究過程中采用一維流動模型。目前氣液兩相流的瞬態模擬常用模型有3 種: 雙流體、 無壓波及漂流模型。 本文選用雙流體模型, 因為上述3 種模型只有雙流體模型針對氣液兩相各自單獨建立了連續性方程和動量方程, 可以對氣液兩相進行更為深入的研究, 精度也優于另外2 種模型。

氣、 液相連續模型:

氣液相動量守恒方程:

式中:φ為截面含氣體積分數, 無因次量;A為管線截面積, m2;HL為常數;p為壓力, Pa;g為重力加速度, m/s2;ρg為氣相密度, kg/m3;vg、vL分別為氣相液相表現流速, m/s;θ為管線傾角,(°)。 ΔmgL為管線氣相轉化液相的質量流量,kg/(m·s) ; ΔmgL為管線液相轉化氣相的質量流量, kg /(m·s) ;Γgw、ΓLw為氣、 液各相與壁面間的剪切力, N/m;Γgi、ΓLi為分別為作用在氣相、 液相截面的剪切應力, N/m;v0為相變流速,m/s, 當mgL＞0 時v0=vL, 當mgL＜0 時v0=vg。

2.2 幾何模型的建立

基于現場常出現的起伏管線軌跡, 建立了如圖7 所示的簡化數學模型。 該模型由100 m 下傾段、底部凹陷段、 100 m 上傾段和頂部凸起段組成。 下傾段模擬實際起伏管線的下坡流動, 上傾段模擬起伏管線的上坡流動。

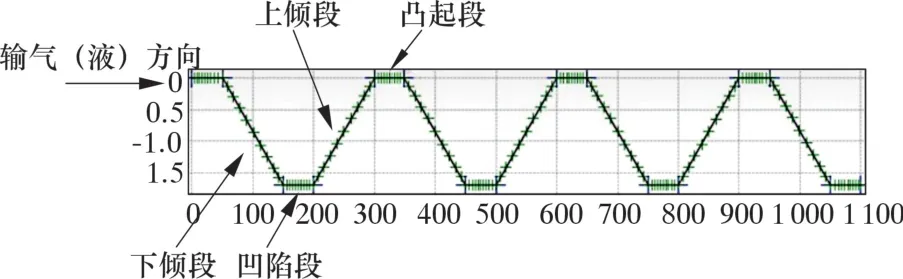
圖7 起伏管線模型Fig.7 Undulating pipeline model

入口設置類型為Mass, 為流量入口, 在此節點設置溫度和流量, 入口溫度設置為32 ℃, 入口氣量為10～200 m3/h, 入口液量為0.1 ～2.0 m3/h;出口設置類型Pressure, 為壓力出口, 在節點設置出口壓力參數及流體數據, 出口壓設置為10 MPa。管線的參數設置: 管徑60 mm、 管線長度13 m、粗糙度5×10-5m 、 傳熱系數6.5 W/(m2·℃) 、 模擬時間設置為60 min。

3 模擬結果分析

3.1 持液率分析

持液率反映管線截面含液體積分數, 能反映起伏管線各個位置液相占比; 攜液量反映當前工況下的氣體攜帶液體的能力; 壓降則反映集輸管線中氣體運移液相的能量變化。 當前工況為液量0.6 m3/h、氣量150 m3/h、 傾斜角6°, 得到起伏管線沿線持液率分布如圖8 所示。

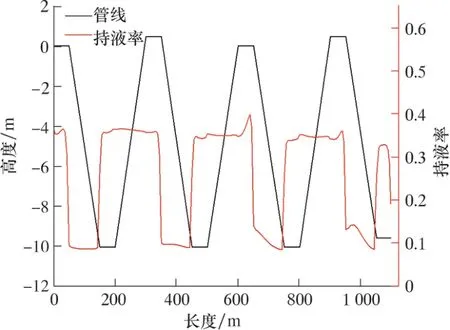
圖8 管線沿線的持液率分布Fig.8 Liquid holdup distribution along the pipeline

由圖8 可以發現, 隨著管線運移, 下傾段持液率逐漸減小, 上傾段持液率逐漸增加。 這說明下傾段依靠自身重力作用液體較容易被帶出, 上傾段由于液相要克服自身重力作用和摩阻阻力較難被帶出。

底部凹陷處到下傾段指端為持液率最大位置,此處為最容易積液位置, 且隨著起伏波的增多, 持液率波動性會在增大。 這是因為積液聚集在底部凹陷處到下傾段指端, 氣體通過這里時會形成活塞式氣頂水效果, 呈現為持液率波動性增大效果。

針對這一現象, 將對上傾段、 凹陷段和凸起段進行單獨分析, 得到持液率和壓降的規律, 如圖9～圖11 所示。

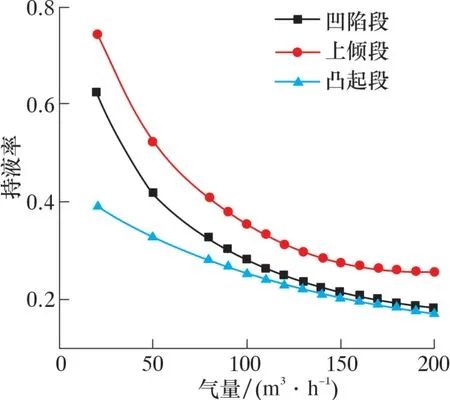
圖9 管線持液率隨氣量變化Fig.9 Liquid holdup vs. gas flow rate

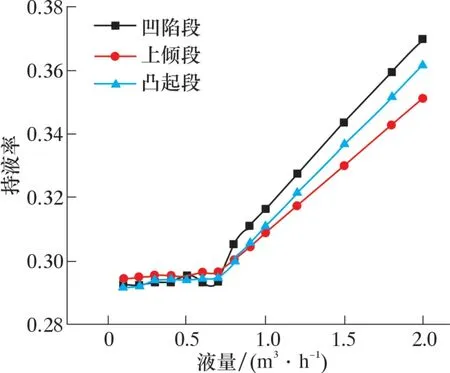
圖10 管線持液率隨液量變化圖Fig.10 Liquid holdup vs. liquid flow rate

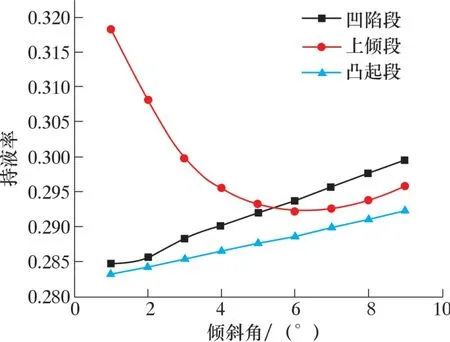
圖11 管線的持液率隨傾斜角變化圖Fig.11 Liquid holdup vs. dip angle

由圖9 可以發現: 隨著氣量增加, 3 種管段持液率均減小; 當氣量大于150 m3/h 時, 攜液難易程度為上傾段＞凹陷段＞凸起段。 這說明上傾段為最難攜液管段。

由圖10 可以發現, 隨著液量增加, 各管段持液率均增加。 其中液量在0.6 m3/h 處存在拐點,當液量大于0.6 m3/h 時, 持液率增加速率會急劇增加。 這說明管線此時液相含量增加, 積液程度會急劇增加, 因此現場集輸管線應注意液量達到0.6 m3/h 后的集輸管線運行狀態。

由圖11 可以發現: 凹陷段和凸起段均隨著傾斜角度的增加持液率逐漸增大, 但變化趨勢不明顯; 對于上傾管路隨著傾角增大會出現先減小后增大趨勢, 這是因為角度小于6°時, 重力分量小,氣體需克服的阻力較小, 隨著角度繼續增大, 重力分量變大, 此時氣相能量不足以帶走管內積液, 所以呈現持液率增大趨勢。

綜合以上分析可以得出, 在較小氣量、 較大液量和較大傾斜角等導致積液的不利條件下, 上傾段和凹陷段最易出現積液, 在制定管線集輸工藝參數時, 應重點考慮水平段和上傾段的臨界攜液能力。前面針對上傾斜管的室內研究能為臨界攜液流速的確定提供測試方法。

3.2 起伏管的壓降分析

當液量為0.6 m3/h、 傾斜角為6°、 氣量為20～200 m3/h 時, 管線總壓降隨氣量的變化如圖12 所示。

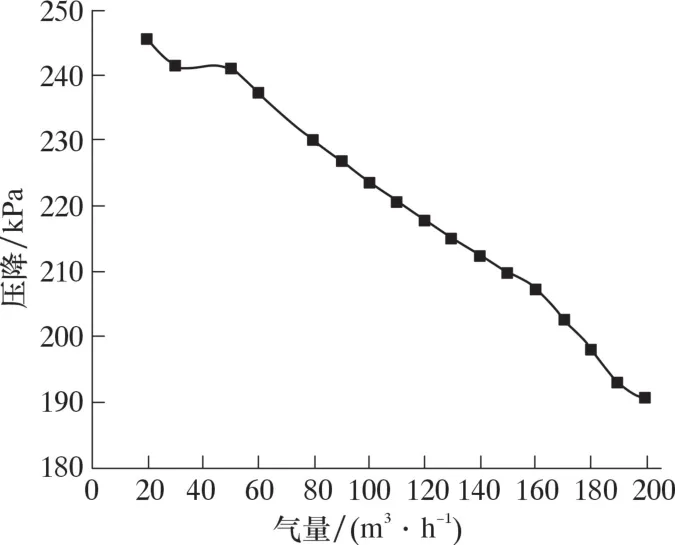
圖12 壓降隨氣量的變化Fig.12 Pressure drop vs. gas flow rate

由圖12 可以發現, 隨著氣量的增加, 壓降呈現出與傾斜管線不同的規律, 為持續下降。 這是因為壓降主要由重位壓降和摩阻壓降組成, 當前氣量范圍下, 重位壓降相較于摩阻壓降占主導地位, 隨著氣量增加持液率減小, 重位壓降逐漸減小, 因此總壓降呈現減小趨勢。 當氣量為150 m3/h、 傾斜角為6°、 液量為0.1～2.0 m3/h 時, 壓降隨液量的變化如圖13 所示。

圖13 壓降隨液量的變化Fig.13 Pressure drop vs. liquid flow rate

由圖13 可以看出, 壓降隨著液量的增加不斷增大, 當液量大于0.5 m3/h 時, 壓降近似呈線性變化。 壓降隨傾斜角的變化如圖14 所示。

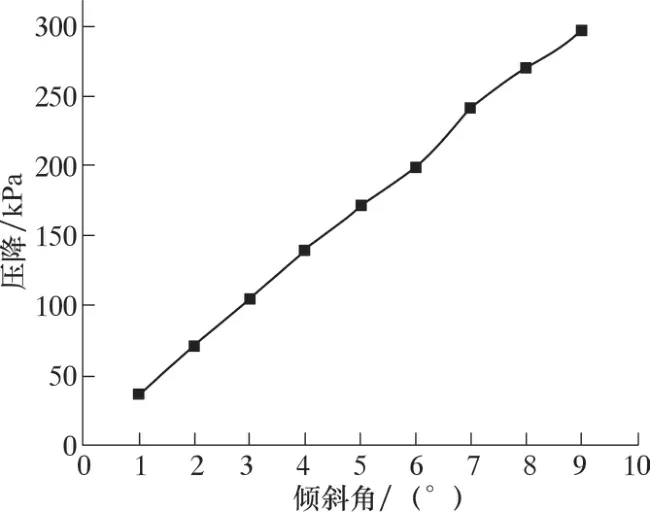
圖14 壓降隨傾斜角度的變化Fig.14 Pressure drop vs. dip angle

由圖14 可以看出, 壓降隨角度呈線性增加趨勢, 這是因為當前角度范圍內, 重位壓降隨著角度增加逐漸增大, 所以呈現出總壓降逐漸增大趨勢。

4 持液率模型建立

由于上傾段最容易積液, 所以對上傾段進行回歸擬合持液率計算模型, 使其能準確預測起伏管路上傾段各個位置持液率。 本次回歸以馬克赫杰-布里爾計算方法為基礎, 根據試驗所測得的數據, 通過回歸分析方法, 給出了氣液兩相持液率計算公式:

其中:

式中:vsl為液相的表觀速度, m/s;vsg為氣相的表觀速度, m/s;σ為液相的表面張力, N/m;μl為液相的黏度, Pa·s;c1～c6均為經驗常數, 詳見表2。

表2 經驗常數Table 2 Empirical constants

帶入試驗數據驗證, 馬克赫杰方法的計算誤差普遍較大, 均在70%以上, 并且預測值普遍比實驗值偏小。 表3 給出了馬克赫杰試驗與本試驗主要條件參數。

表3 馬克赫杰試驗與本試驗對比Table 3 Comparison between Mukherjee's experiment and this paper's experiment

由表3 可見, 2 種方法試驗條件相差較大, 因此需要對參數進行重新擬合。

基于馬克赫杰持液率相關式連續性較好、 考慮因素全面等優點, 選擇對其關系式中的經驗常數進行修正。 根據馬克赫杰給出的氣液兩相流持液率關系式, 對試驗的持液率Hl與馬克赫杰給出的相關準數Nvl、Nvg、Nl的關系進行擬合。 經擬合得到新的經驗常數和經修正后的持液率誤差分別如表4所示。

表4 新的經驗常數Table 4 New empirical constants

使用新的參數計算之后的各角度持液率平均誤差見表5, 誤差均在5%以內。

表5 不同角度修正后持液率計算平均誤差Table 5 Average errors for liquid holdup corrected for different dip angles

5 結 論

本文基于起伏管路進行數值模擬和室內模擬試驗研究, 得到以下結論:

(1) 通過對起伏管線進行數值模擬研究發現,凹陷段和上傾段極易積液, 且隨著氣量增大, 3 種管線持液率減小程度依次為: 凸起段＞凹陷段＞上傾段; 上傾管線中, 6°為持液率最低點, 此時液體最容易被帶出; 上傾管線中, 壓降隨角度為線性增大。

(2) 通過室內試驗發現, 35 ～70 m3/h 時攜液量波動較明顯, 此時易形成段塞流, 因此集輸管線此工況下應注意段塞流對管線的損傷; 通對管路壓降分析可得造成壓力損失最大位置為凹陷管和凸起管處。

(3) 通過數值模擬結果與試驗結果比對發現,模擬結果與試驗結果非常接近, 這說明OLGA 軟件計算的準確性較高; 基于馬克赫杰-布里爾計算方法通過試驗數據擬合得到適用于起伏管路上傾段的持液率預測式, 帶入試驗數據驗證發現誤差均在5%以內。