面向多點偵察和通信服務的多無人機協同任務分配

姚昌華 安蕾 劉鑫 韓貴真 高澤郃

摘要針對多無人機對多個異構任務目標進行偵察和通信服務的協同優化問題，通過考慮不同目標的任務要求和價值，以及多機協同增益與任務行為制約關系，構建斯坦伯格博弈模型，將上層無人機建立為博弈領導者，下層無人機建立為博弈的跟隨者，并提出一種分布式策略更新迭代算法，實現了多無人機任務分配方案的穩定收斂以及系統任務收益優化．仿真結果顯示，所提方法能有效提升多無人機系統同時完成多個任務的效益，并能在不同環境下實現面向異構任務價值的高效協同．

關鍵詞多無人機系統;任務分配;斯坦伯格博弈;迭代算法

中圖分類號

TN929.5;V279

文獻標志碼

A

收稿日期

2021-08-16

資助項目

國家自然科學基金（61971439，61961010）;江蘇省自然科學基金（BK20191329）;中國博士后科學基金（2019T120987）;南京信息工程大學人才啟動經費（2020r100）

作者簡介

姚昌華，男，博士，教授，研究方向為智能無人集群、智能無線通信．ych2347@163.com

安蕾（通信作者），女，碩士生，研究方向為智能無人集群．1178535838@qq.com

0 引言

隨著人工智能技術的快速發展，無人機的智能化水平也越來越高，數量眾多的無人機組成無人機群以其高度的靈活性、廣泛的適應性、可控的經濟性，擁有越來越廣泛的應用潛力．無人機可以對地面目標近距離地實施選擇性和針對性的觀測和通信［1］．多無人機系統具有容錯性強、自適應性好等優勢，更適合在復雜環境下執行任務［2］．

多無人機執行任務時，必須對其進行任務分配，以提高任務執行效率．無人機集群的任務規劃是指根據任務需求、自身特性等對目標任務進行綜合調度，從而建立無人機與任務目標之間合理的映射協同關系［3-4］．對于異構主體之間的協同問題，已有了一些相關研究，比如：文獻［5］采用多架無人機協同輔助實施任務分配和路徑優化的分層優化方案，能夠解決降低時間和能耗的優化問題;文獻［6］針對多無人機作戰飛機協同任務分配問題建立了一種擴展的多目標整數規劃模型，并采用改進的量子粒子群算法求解最優方案;文獻［7］針對任務隨機下發場景中由于任務完成時間約束帶來的任務完成度低的問題，通過強化學習方法進行無人機的行為決策，達到新任務與正在執行任務的動態分配以提高任務完成度;文獻［8］考慮飛行航程和任務分配均衡性，在自適應遺傳算法運行過程中對交叉率和變異率進行實時動態調整，以克服標準遺傳算法陷入局部最優的缺點;文獻［9］針對多目標跟蹤任務分配中傳感器之間競爭與合作的關系，提出了一種基于博弈理論的多目標跟蹤任務傳感器資源分配方法;文獻［10］考慮在通信帶寬有限條件下多無人機組隊的任務分配問題，通過協調偵察、執行和評估任務，改進基于一致性的競拍算法來減少通信負擔;文獻［11］基于相鄰局部通信的分布式拍賣算法，實現了多無人機任務協同分配的優化求解問題;文獻［12］采用多無人機輔助移動邊緣計算系統聯合優化一個有限周期內的無人機軌跡和用戶調度;文獻［13］考慮任務分配中聯盟的構建和無人機資源管理方法，使聯盟中各無人機能夠以更加平衡的方式消耗資源，提升系統性能;文獻［14］綜合考慮無人機的物理性能約束，應用基于模擬退火的混合粒子群算法進行任務分配求解;文獻［15］建立多任務的分配問題模型，采用多余負載競拍方案減少非法劣解，通過實數編碼建立粒子和實際分配方案之間的映射關系，解決實際分配問題;文獻［16］研究了MEC輔助無人機群中所有成員的總延遲的最小化問題，提出卸載模型，縮短了任務的完成時間;文獻［17］提出一種動態分散任務分配算法，用于任務分配問題中在線新任務的分配．

上述文獻所研究的任務目標大多是同構的［9，12，16-17］，未考慮異構的任務價值［10-11，13］，也未考慮同時存在多點偵察任務和通信服務．從方法上看，現有多數研究基于集中式分配算法［5-8，14-15］，即需要一個中心控制實體來為集群內的所有成員分配任務．這種模式不利于提高無人機集群的魯棒性和環境適應能力．在無人機集群執行任務過程中，大部分的環境狀態都是動態變化的，其任務分配的方案也應該隨時優化調整，以有效應對動態環境的變化．集中式任務分配算法存在計算復雜度高、依賴中心節點等問題．研究自適應強的多無人機分布式動態任務分配方法，是多無人機協同任務分配的現實需要，也是難點問題．

本文研究多無人機網絡中的任務目標調度問題，構建面向異構任務類型和價值的斯坦伯格（Stackelberg）博弈模型，設計通信和偵察的任務效用函數，并提出分層用戶偵察和通信任務調度以及功率控制算法，實現基于無人機自主任務選擇的多無人機系統任務分配穩定收斂以及系統任務總收益優化．

1 系統模型和問題建模

1.1 系統模型

無人機通信偵察任務分配系統模型如圖1所示，由一個領頭無人機（Leader Drone，LD）和隨機分布在其周圍的N個協同無人機（Collaborative Drone，CD）構成，共同完成多個任務．每一架無人機監測或服務范圍內均有隨機分布的不同數量的通信和偵察兩類任務．每個任務的重要程度或屬性不同，其對應的任務價值也不同．各架無人機根據自身位置與目標之間的距離、目標價值、偵察或通信服務所獲得的期望收益，以及與其他無人機通信鏈路之間可能的干擾關系，來自主決定選擇任務對象．

令0表示領頭無人機，則分布在周圍的協同無人機集合表示為A=｛CD 1，CD 2，…，CD N｝，領頭及協同無人機可調度通信任務目標集合表示為T u，i=｛1，2，…，m｝，i∈A∪｛0｝，可調度的偵察任務目標集合表示為T z，i=｛1，2，…，n｝．信道增益為g i，j，j∈T u，i∪T z，i∪｛0｝，并且假定信道增益在任務目標調度和功率調整時期穩定不變．LD和CD的發射功率向量為p=［p 0，p 1，…，p N］，背景干擾噪聲功率為σ2．CD執行通信偵察任務后，需要將信息上傳匯報給領頭無人機．偵察任務中，每一架無人機對各個任務目標對象的分辨率r為定值，構建分辨率矩陣．通信任務調度中，當給定LD以及其他CD的調度策略后，CD i服務第k個通信任務目標的下行信噪比為

γk i（p i，p -i）=p ig i，kIk i（p -i），? （1）

通信信息上傳時的信噪比為

k i（p i，p -i）=p i，0g i，0Ik i（p -i，0），? （2）

其中Ik i（p -i）=p 0g 0，k+∑j≠i，j∈Ap jg j ，k+σ2，Ik i（p -i，0）=∑j≠i，j∈Ap j，0g j，0+σ2，p -i=［p 0，p 1，…，p i-1，p i+1，…，p N］表示除CD i以外的所有無人機的功率分配向量.CD i下的通信任務目標同時收到來自鄰居CD的同層干擾以及來自LD的跨層干擾．p i，0為通信上傳功率值，假定CD到LD通信上傳速率為R i，分配帶寬為 i，由R i= ilog 21+p i，0g i，0σ2可求得p i，0．另外，LD服務的第l個通信任務目標的下行信噪比可以表示為

γl 0（p 0，p -0）=p 0g 0，lIl 0（p -0）=p 0g 0，l∑j∈Ap jg j，l+σ2．（3）

1.2 斯坦伯格分層博弈模型

在本文多無人機系統協同模型中，任務類型包含通信任務和偵察任務兩類．因目標任務的重要程度不同，需要對LD和CD任務執行進行合理規劃，任務目標重要程度較高的服務質量（QoS）需要首先得到保障．本文基于任務優先級以及任務目標需求的差異性，采用分層博弈模型來刻畫領頭無人機和協同無人機之間的任務目標調度和功率分配問題．在該博弈中，先做出決策的一方為領導者（leader），其余觀測領導者的決策從而做出行動的一方稱為跟隨者（follower）．本文將上層領頭無人機視為領導者，下層協同無人機視為跟隨者，利用分層斯坦伯格（Stackelberg）博弈模型刻畫LD-CD之間的分層競爭交互關系．目標任務調度中，Stackelberg定義為

G=｛A，｛P 0，C 0｝，｛P i，C i｝ i∈A，｛U 0｝，｛U i｝ i∈A｝，? （4）

其中｛P 0，C 0｝和｛P i，C i｝ i∈A分別表示LD和CD的策略空間，｛U 0｝和｛U i｝ i∈A分別表示LD和CD執行目標任務效用函數．

對于執行通信服務任務的無人機，無人機效用函數的設計同時考慮了目標任務的滿意度和功率消耗．對于給定的通信目標k，LD的效用函數可以表示為

Uk 0（p 0，p -0）=Uk 0（p 0，p -0）-Ck 0（p 0，p -0）=

11+exp（-αk 0（γk 0-βk 0））·v k-μ 0p 0.? （5）

該效用函數包含兩部分：第一部分為服務通信任務目標對象的收益Uk 0（p 0，p -0） ，被建模為S型函數，代表所服務通信目標任務的滿意度;第二部分是代價函數Ck 0（p 0，p -0），表示動態的功率開銷，其中的參數α 0和β 0分別為S型函數的陡度和中心值．v k代表通信任務目標k的價值．μ 0為常數，用來權衡服務目標的滿意度和功率能量消耗．當給定CD i服務第k個通信任務目標時，其效用函數可以表示為

Uk i（p i，p -i）=Uk i（p i，p -i）-Ck i（p i，p -i）=

11+exp（-αk i（γk i+θk i-βk i））·v k-

μ ip i-λ ig i，0p i-κ ip i，0，? （6）

其中，CD i的收益函數部分同時考慮了服務通信任務目標對象的滿意度和通信上傳的滿意度，θ為常數，用于折中通信下行信噪比和上傳信噪比．此外α i和β i分別為函數陡度和中心值．CD i代價函數部分同時考慮了執行目標任務的功率消耗、上傳通信信息的功率消耗和下層CD i對上層LD通信服務的干擾懲罰．κ i表示上傳通信信息功率消耗系數，λ i表示干擾懲罰參數，用于調節跨層干擾對上層服務目標的影響．當CD i增加發射功率時，服務任務目標對象的滿意度增加，同時將會對上層LD帶來更高的跨層干擾，影響LD服務任務目標的QoS，因此CD i需要進行折中優化．

對于執行偵查服務任務的無人機，無人機偵察效用函數的設計同樣包括目標任務的滿意度和功率消耗兩部分.偵察目標任務調度中，每一架無人機對各個任務目標的分辨率為定值，構建分辨率矩陣．給定LD服務偵察任務目標時，其偵察效用函數可以表示為

Ux 0=Ux 0-Cx 0=

v x1+exp-αx 0 rx 0dx 0 ·p′ 0-βx 0 -δ 0p′ 0. （7）

該效用函數包括兩個部分，Ux 0 表示服務偵察任務目標的收益，Cx 0 表示服務偵察目標的代價，即LD圖像識別的功率消耗．其中，rx 0 為LD對任務目標的分辨率，dx 0 為LD與任務目標距離，偵察收益建模為S型函數，δ 0為圖像識別功率消耗比例常數．當給定CD i服務偵察任務目標x時，其偵察效用函數可以表示為

Ux i=Ux i-Cx i=

v x1+exp-αx i rx idx i τx i p′ i-βx i -

ig i，0（1-τ i）p′ i-δ iτ ip′ i，? （8）

其中代價函數部分同時考慮了圖像上傳的功率消耗和LD識別的功率消耗，p′ i 為每個CD i進行偵察任務的總功率，τ i用于識別計算處理的功率比例，1-τ i表示識別完成后偵察信息上傳功率消耗比例， i為偵察信息上傳干擾懲罰參數，用來權衡偵察信息上傳對領頭無人機產生的干擾，δ i為常數，權衡CD i用于拍照的功率消耗，默認δ 0=δ i．

2 斯坦伯格均衡求解

定義符號Φ i=｛p i，c i｝，Φ -i=｛Φ 0，Φ 1，…，Φ i-1，Φ i+1，…，Φ N｝，Φ m=｛Φ 1，Φ 2，…，Φ N｝．

定義1 （斯坦伯格均衡，Stackelberg Equilibrium，SE）［18］ Φ* 0 表示上層博弈最大化效用函數的最佳相應策略，Φ* m 表示下層博弈的最佳響應策略．對于任意的策略組合，均滿足以下條件：

U 0（Φ* 0，Φ* m）≥U 0（Φ 0，Φ* m），? （9）

U i（Φ* i，Φ* -i）≥U i（Φ i，Φ* -i）．? （10）

（Φ* 0，Φ* m）稱為斯坦伯格均衡．LD最優策略由下層博弈最佳響應策略給定，最大化自身效用函數求解．同理，CD的最優策略是由給定上層博弈的最佳相應策略，最大化自身效用函數求解．通過逆向遞推法尋求上下兩層子博弈的均衡，如圖2所示．

2.1 下層均衡求解

給定上層LD的任務目標選擇和發射功率，每一個CD獨立地選擇最佳策略來最大化自身效用函數，因此，下層子博弈定義為

G=｛A，｛Φ i｝ i∈A，｛U i｝ i∈A｝．? （11）

定理1 給定其他無人機的策略Φ -i，CD i最優的通信任務目標選擇：

t* i=arg maxg i，kIk i（p -i）+θε ig i，0Ik i（p -i，0）v k．? （12）

證明 當給定其他無人機策略Φ -i，令p i，0=ε ip i，Λ i=g i，kIk i（p -i）+θε ig i，0Ik i（p -i，0），CD i服務于任意兩個通信任務目標k和l，假定Λk i≥Λl i，v k≥v l，顯然，γk i+θk i≥γl i+θl i，然后計算服務不同任務目標的效用差值為

Uk i-Ul i=Uk i-Ul i=

v k1+exp（-α i（γk i+θk i-β i））-

v l1+exp（-α i（γl i+θl i-β i））≥0. （13）

因此，CD i最優通信任務目標t* i=arg maxg i，kIk i（p -i）+θε ig i，0Ik i（p -i，0）v k，定理1得證．

CD i通過定理1確定最優通信任務目標，然后進一步優化發射功率最大化效用函數．為方便求解，令Γ i=γt i i+θt i i，pt i i，0=ε ipt i i，其Ut i i 對p i求偏導得：

dUt i idp i=Ut i i ′（Γ i）d（Γ i）dp i-dC idp i．? （14）

令dUt i idp i=0，即得：

Ut i i ′（Γ i）d（Γ i）dp i=dC idp i．? （15）

令g i，t iIt i i（Φ -i）+θε ig i，0It i i（Φ -i，0）=1B i，即得：

Ut i i ′（Γ i）=（μ i+κ iε i+λ ig i，0）×B i．? （16）

令Ψ（Γ i）=Ut i i ′（Γ i），可得：

Γ i=Ψ-1［Ut i i ′（Γ i）］=? Ψ-1［（μ i+κ iε i+λ ig i，0）×B i］．（17）

S型函數倒數滿足以下關系：

Ut i i ′（Γ i）=α iUt i i（Γ i）［1-Ut i i（Γ i）］．（18）

根據式（16）和式（18）可得：

p* i=B iβ i-B iα i×lnA i2-1-A i2-12-1，? （19）

其中A i=α i×v t i（μ i+κ iε i+λ ig i，0）×B i.下層調度通信任務目標和上傳信息總信噪比和為

Γ i=β i-1α i×lnA i2-1-A i2-12-1．（20）

CD的通信效用函數即可轉化為

Ut i i（Γ i）=v t i1+exp（-α i（Γ i-β i））-? （μ i+κ iε i+λ ig i，0）·B i·Γ i．? （21）

通過式（18）和代價直線是一條過原點的切線［19］可得：

U′ i（Γ i）Γ i=U i（Γ i）．（22）

經過運算參數β i可以設置如下：

β i=Γ i-ln（α iΓ i-1）α i．? （23）

同理，令p′ i=p i，偵察效用值由式（8）求得，比較所有偵察任務目標效用值，選擇最優偵察任務目標x* i．若效用值為負，此時p′ i=0，選擇放棄該任務目標的偵察任務．分析通信偵察效用值，確定最優的任務目標選擇為c* i.假設對于任意的i，B i·Ψ-1［（μ i+κ iε i+λ ig i，0）×B i］在區間［L i，H i］上為增函數，其中g i，t iIt i i（Φ -i）+θε ig i，0It i i（Φ -i，0）=1B i，L i=min［L1 i，L2 i，…，Lm i］，H i=max［H1 i，H2 i，…，Hm i］．下層迭代中CD的功率控制形式為pt* i i（k+1）=min［p1 i（k+1），p2 i（k+1），…，pm i（k+1）］，其中pt i i（k+1）=Ft i i（p（k））．令F i（p（k））=min［F1 i（p（k）），F2 i（p（k）），…，Fm i（p（k））］，最終功率更新迭代和服務任務目標迭代策略為

p* i（k+1）=F i（p（k）），? （24）

c* i（k+1）=arg max（Ut* i i，Ux* i i）．? （25）

下層博弈中，上述任務目標選擇和策略更新迭代過程最終收斂在唯一的納什均衡點.下面引入標準干擾函數相關內容輔助證明．

定義2（唯一性證明）［20］ 如果函數F（p）滿足以下條件，則該函數為標準干擾函數：

1）非負性：F（p）>0;

2）單調性：對于任意p1>p2，則F（p1）>F（p2）;

3）伸縮性：對于任意τ>1，則τF（p）>F（τp）．

如果函數F1（p）和F2（p）為標準干擾函數，其組合函數也必然滿足標準函數特性；如果博弈參與者最佳響應函數為標準干擾函數，則該博弈必然存在唯一的納什均衡解．

定理2 下層博弈中CD服務通信任務目標的功率迭代更新為標準干擾函數，即p* i（k+1）=F i（p（k）），將從任意可行的初始值收斂到唯一的納什均衡點．

證明 對于CD i中任意一個任務目標t i，即pt i i=Ft i i（p），則有

Ft i i（p）=B i·Γ i=B i·Ψ-1［（μ i+κ iε i+λ ig i，0）×B i］，

其中g i，t iIt i i（Φ -i）+θε ig i，0It i i（Φ -i，0）=1B i．下層CD策略調整時，由于上層LD的策略是固定不變的，下層其他CD的策略也不會影響當前CD策略，只受其余CD發射功率的影響，因此It i i（Φ -i）=It i i（p -i）．

1）非負性：由于背景噪聲非零，因此B i>0，非負性滿足條件．

2）單調性：如果p1>p2，則It i i（p1 -i）>It i i（p2 -i），It i i（p1 -i，0）>It i i（p2 -i，0），因為函數B i·Ψ-1［（μ i+κ iε i+λ ig i，0）×B i］在區間［L i，H i］上為增函數，其中L i=min［L1 i，L2 i，…，Lm i］，H i=max［H1 i，H2 i，…，Hm i］，因此Ft i i（p1）>Ft i i（p2），單調性滿足條件．

3）伸縮性：對于任意τ>1，則有

Fm i（τp）-τFm i（p）=

1η 1·Ψ-1ω×1η 1-τ1η 2·Ψ-1ω×1η 2<

1η 1·Ψ-1ω×1η 2-τ1η 2·Ψ-1ω×1η 2<0，

其中η 1=g i，mIm i（τp -i）+θε ig i，0Im i（τp -i，0），η 2=g i，mIm i（p -i）+θε ig i，0Im i（p -i，0），ω=μ i+κ iε i+λ ig i，0．因此，伸縮性滿足條件．故pt i i（k+1）=Ft i i（p（k））為標準干擾函數．假定第k+1次迭代，服務的通信任務目標為t* i（k+1），功率更新迭代可得：

pt* i i（k+1）=min［p1 i（k+1），p2 i（k+1），…，pm i（k+1）］=

min［F1 i（p（k）），F2 i（p（k）），…，Fm i（p（k））］．

因F1 i（p（k）），F2 i（p（k）），…，Fm i（p（k））均為標準干擾函數，由此可得pt* i i（k+1）=F i（p（k））為標準干擾函數，下層子博弈迭代更新函數必然存在唯一的納什均衡解，得證．

2.2 上層均衡求解

上層子博弈定義為

G=｛｛0｝，｛Φ 0｝，｛U 0｝｝， （26）

則其LD最優的通信任務目標選擇為

t* 0=arg maxg 0，kIk 0（p -0）·v k. （27）

同理，進一步優化發射功率最大化效用函數可得：

p* 0=B 0γ 0=B 0β 0-B 0α 0×lnA 02-1-A 02-12-1， （28）

Ut 0 0（Γ 0）=v t 01+exp（-α 0（γ 0-β 0））-μ 0·B 0·γ 0， （29）

其中B 0=Ik 0（p -0）g 0，k，A 0=α 0·v t 0μ 0·B 0．上層偵察任務目標效用值由式（7）求得，比較所有偵察任務效用值，選擇最優偵察任務目標x* 0．類似于下層子博弈的迭代更新，LD的功率迭代更新為

pt* 0 0（k+1）=min［p1 0（k+1），p2 0（k+1），…，pm 0（k+1）］=

min［F1 0（p（k）），F2 0（p（k）），…，Fm 0（p（k））］.? （30）

因此，LD服務任務目標和功率更新策略為

p* 0（k+1）=F 0（p（k）），? （31）

c* 0（k+1）=arg max（Ut* 0 0，Ux* 0 0）．（32）

3 算法流程

子博弈循環采用一般迭代算法求解，達到斯坦伯格均衡迭代結束，上下層目標任務分配不再改變．具體流程如圖3所示．

4 仿真分析

對于無人機位置、無人機所服務的通信和偵察任務目標個數、通信和偵察任務目標價值等信息構建場景進行仿真分析，同時通過調整無人機位置，設定不同場景對上下層博弈交互進行迭代更新，驗證算法的收斂性．

4.1 參數設置

場景設置參數如下：LD可服務任務目標區域半徑為500 m，10個CD隨機分布在LD調度范圍內，其可服務任務目標半徑為80 m，通信和偵察任務隨機分布在LD和CD服務范圍內．LD可服務的通信任務目標和偵察任務目標均為3個． CD可服務的通信和偵察任務目標個數分別依次為4、5、4、5、4、4、5、3、4、3和3、4、2、4、3、2、4、1、2、2．LD所服務的通信和偵察任務目標價值v=1，CD所服務的通信和偵察任務目標價值相對較低，取值在［0.9，0.95］內隨機生成． 其中CD i到任務目標j的信道增益g i，j=d-2 i，j，d-2 i，j表示對應的距離，信號衰減為25 dB．LD所服務通信任務目標信噪比為γ 0=30 dB，CD所服務通信任務目標的信噪比和上傳信噪比均在［10，20］dB內隨機生成．噪聲功率σ2=10-8 mW．參數α i=0.2，θ=1，β i由式（23）確定．通信干擾懲罰和干擾代價參數設置為λ i=108，μ i=1，上傳功率消耗參數為κ i=1．偵察任務中LD識別圖像功率消耗δ 0=1，CD識別圖像功率消耗δ i=1，上傳干擾懲罰和上傳功率比例參數設置為 i=108，τ i=0.6．表1中給出了LD和CD對偵察任務目標對象的分辨率大小．上述參數在后面仿真中均保持不變．圖4中給出兩種無人機不同位置下的仿真場景．

4.2 結果分析

圖5給出了場景1和場景2中相應的LD和CD的效用迭代更新曲線，每一輪迭代15次，共設置20輪，橫坐標為迭代輪數，縱坐標為各無人機效用值．給定上層的目標任務選擇后，下層為滿足通信任務目標的最小信噪比需求進而優化最小的發射功率，在每一輪的15次迭代的過程中，由于功率在增大，各協同無人機之間的同層干擾逐漸增大，需要不斷地增大功率滿足信噪比需求，不斷迭代直至下層穩定．上層迭代過程中，由于協同無人機的功率在增大，跨層干擾在增大，領頭無人機需要增大發射功率滿足自身的信噪比需求，直至上層穩定．結合圖6中場景1和場景2中相應的LD和CD的各輪目標的迭代變化曲線，分析得出效用曲線中的轉折點為無人機依據效用值的變化選擇偵察任務目標．從效用的更新曲線來看，上下層博弈交互迭代后最終均能夠達到收斂狀態，驗證了所提算法的收斂性能．

表2中給出了上下層子博弈達到斯坦伯格均衡時無人機最優通信和偵察任務分配結果．各無人機能夠自主進行服務通信或偵察目標優化分配．其中，T u，0為領頭無人機通信任務目標，T z，0為領頭無人機偵察任務目標，T u，1～T u，10為各協同無人機的通信任

務目標，T z，1～T z，10為各協同無人機的偵察任務目標（以T u，0=1為例，表示領頭無人機均衡下選擇1號通信任務目標）．

4.3 系統效用對比

圖7a與7b中給出了任務目標調度過程中聯合考慮通信和偵察任務、只考慮通信任務和只考慮偵察任務三種狀態下的系統效用值變化．在所用算法下，考慮通信任務的收益由于需要滿足信噪比需求，功率增大過程中同層和跨層干擾在增大，使得在決策過程中效用值呈現下降的趨勢．可以看出，上下層博弈最終收斂至均衡點，所用算法的系統效用值均大于只考慮通信或者偵察單個指標．圖7c與7d中聯合考慮通信偵察任務下依據所用算法、最大任務目標價值和隨機決策三種方法進行任務目標選擇，橫坐標為迭代輪數，縱坐標為系統效用值，可以看出，所用算法系統效用值均大于依據最大價值選擇和隨機決策兩種方法，并能夠有效提高多無人機系統的整體效用．

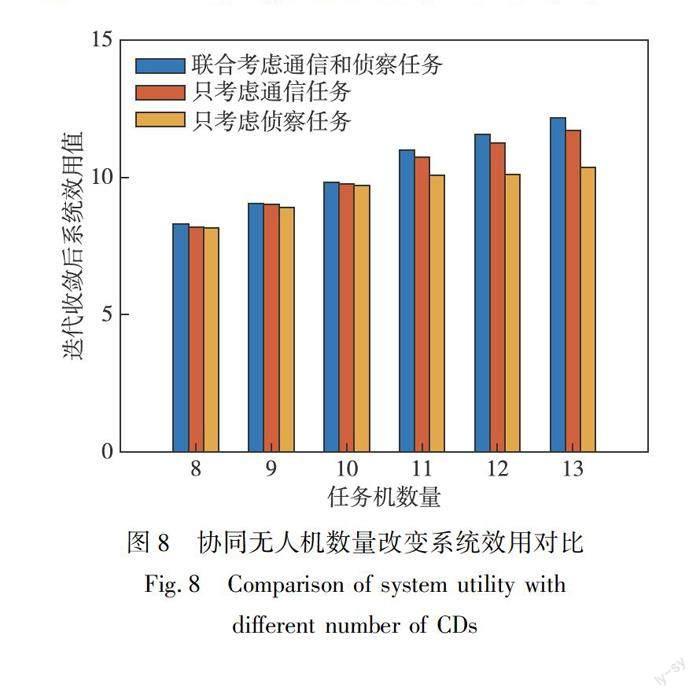
圖8分別給出了8、9、10、11、12、13架協同無人機情況下系統的效用值對比．協同無人機數量的改變構成不同的場景，可以看出，上下層博弈交互迭代達到斯坦伯格均衡后，聯合考慮通信偵察任務的效用值均大于考慮通信或者偵察單個指標情況．

5 結束語

多無人機通信和偵察任務分配在無人集群網絡優化中具有重要的研究意義．本文聚焦于無人機網絡中目標調度和功率控制的聯合優化，利用分層博弈框架分析領頭無人機和協同無人機的決策行為，采用分布式策略迭代更新算法求解Stackelberg均衡，實現無人機最優目標任務調度．對多個場景進行仿真分析，驗證了所提算法能夠在多無人機系統中實現分布式任務分配的收斂和系統穩定，并有效提高了多無人機系統遂行任務的整體效用．

參考文獻

References

［1］ 宗群，王丹丹，邵士凱，等.多無人機協同編隊飛行控制研究現狀及發展［J］.哈爾濱工業大學學報，2017，49（3）：1-14

ZONG Qun，WANG Dandan，SHAO Shikai，et al.Research status and development of multi UAV coordinated formation flight control［J］.Journal of Harbin Institute of Technology，2017，49（3）：1-14

［2] 張可為，趙曉林，李宗哲，等.多無人機偵察任務分配方法研究綜述［J］.電光與控制，2021，28（7）：68-72，82

ZHANG Kewei，ZHAO Xiaolin，LI Zongzhe，et al.A review of multi-UAV reconnaissance mission assignment methods［J］.Electronics Optics ＆ Control，2021，28（7）：68-72，82

［3] Zhang L，Zhu Y A，Shi X C.A hierarchical decision-making method with a fuzzy ant colony algorithm for mission planning of multiple UAVs［J］.Information，2020，11（4）：226

［4] Huang T Y，Wang Y，Cao X W，et al.Multi-UAV mission planning method［C］／／2020 3rd International Conference on Unmanned Systems（ICUS）.November 27-28，2020，Harbin，China.IEEE，2020：325-330

［5] Du X Y，Guo Q C，Li H，et al.Multi-UAVs cooperative task assignment and path planning scheme［J］.Journal of Physics：Conference Series，2021，1856（1）：012016

［6] 趙雪森，王社偉，邵校.基于改進量子粒子群優化算法的多UCAV協同任務分配研究［J］.四川兵工學報，2015，36（10）：120-124

ZHAO Xuesen，WANG Shewei，SHAO Xiao.Cooperative task allocation for multiple UCAV based on improved quantum-behaved particle swarm optimization algorithm［J］.Journal of Sichuan Ordnance，2015，36（10）：120-124

［7] 唐峯竹，唐欣，李春海，等.基于深度強化學習的多無人機任務動態分配［J］.廣西師范大學學報（自然科學版），2021，39（6）：63-71

TANG Fengzhu，TANG Xin，LI Chunhai，et al.Dynamic task allocation method for UAVs based on deep reinforcement learning［J］.Journal of Guangxi Normal University（Natural Science Edition），2021，39（6）：63-71

［8］ 王樹朋，徐旺，劉湘德，等.基于自適應遺傳算法的多無人機協同任務分配［J］.電子信息對抗技術，2021，36（1）：59-64

WANG Shupeng，XU Wang，LIU Xiangde，et al.Cooperative task assignment for multi-UAV based on adaptive genetic algorithm［J］.Electronic Warfare Technology，2021，36（1）：59-64

［9] Quan B，Lu X M，Zhang Y M，et al.A multi-objective tracking task assignment algorithm based on game theory［J］.Journal of Physics：Conference Series，2021，1802（3）：032115

［10] Fu X W，Pan J，Gao X G，et al.Task allocation method for multi-UAV teams with limited communication bandwidth［C］／／2018 15th International Conference on Control，Automation，Robotics and Vision（ICARCV）.November 18-21，2018，Singapore.IEEE，2018：1874-1878

［11] 邸斌，周銳，丁全心.多無人機分布式協同異構任務分配［J］.控制與決策，2013，28（2）：274-278

DI Bin，ZHOU Rui，DING Quanxin.Distributed coordinated heterogeneous task allocation for unmanned aerial vehicles［J］.Control and Decision，2013，28（2）：274-278

［12] 嵇介曲，朱琨，易暢言，等.多無人機輔助移動邊緣計算中的任務卸載和軌跡優化［J］.物聯網學報，2021，5（1）：27-35

JI Jiequ，ZHU Kun，YI Changyan，et al.Joint task offloading and trajectory optimization for multi-UAV assisted mobile edge computing［J］.Chinese Journal on Internet of Things，2021，5（1）：27-35

［13] 陳璞，嚴飛，劉釗，等.通信約束下異構多無人機任務分配方法［J］.航空學報，2021，42（8）：306-319

CHEN Pu，YAN Fei，LIU Zhao，et al.Communication-constrained task allocation of heterogeneous UAVs［J］.Acta Aeronautica et Astronautica Sinica，2021，42（8）：306-319

［14] 潘楠，劉海石，陳啟用，等.多基地多目標無人機協同任務規劃算法研究［J］.現代防御技術，2021，49（2）：49-56

PAN Nan，LIU Haishi，CHEN Qiyong，et al.Study on cooperative mission planning algorithm for multi-base and multi-target UAV［J］.Modern Defense Technology，2021，49（2）：49-56

［15] 蔣碩，袁小平.改進PSO算法在多無人機協同任務分配中的應用［J］.計算機應用研究，2019，36（11）：3344-3347，3360

JIANG Shuo，YUAN Xiaoping.Application of improved PSO algorithm in multi UAV cooperative task allocation［J］.Application Research of Computers，2019，36（11）：3344-3347，3360

［16] Chen R F，Cui L，Zhang Y L，et al.Delay optimization with FCFS queuing model in mobile edge computing-assisted UAV swarms：a game-theoretic learning approach［C］／／2020 International Conference on Wireless Communications and Signal Processing（WCSP）.October 21-23，2020，Nanjing，China.IEEE，2020：245-250

［17] Buckman N，Choi H L，How J P.Partial replanning for decentralized dynamic task allocation［C］／／AIAA Scitech 2019 Forum.San Diego，California.Reston，Virginia：AIAA，2019.DOI：10.2514／6.2019-0915

［18] 楊婷婷，宋緋，孫有銘，等.面向異構無人機中繼網絡的負載均衡：一種分層博弈方法［J］.通信技術，2018，51（11）：2619-2626

YANG Tingting，SONG Fei，SUN Youming，et al.Load balancing in heterogeneous UAV relay network：a Stackelberg game method［J］.Communications Technology，2018，51（11）：2619-2626

［19] Xiao M B，Shroff N B，Chong E K P.A utility-based power-control scheme in wireless cellular systems［J］.IEEE／ACM Transactions on Networking，2003，11（2）：210-221

［20] Sun Y M，Wang J L，Sun F G，et al.Energy-aware joint user scheduling and power control for two-tier femtocell networks：a hierarchical game approach［J］.IEEE Systems Journal，2018，12（3）：2533-2544

Multi-UAV cooperative task allocation for multi-point

reconnaissance and communication service

YAO Changhua1 AN Lei1 LIU Xin2 HAN Guizhen1 GAO Zehe1

1School of Electronics ＆ Information Engineering，Nanjing University of Information Science ＆ Technology，Nanjing 210044

2College of Information Science and Engineering，Guilin University of Technology，Guilin 541006

Abstract Aiming at the collaborative optimization of multi-UAV reconnaissance and communication service for multiple heterogeneous targets，the Stackelberg game model is constructed by considering the mission requirements and target values，as well as the restriction between multi-UAV coordination gain and task behavior.The upper-level drone is established as the leader of the game，while the lower-level drones are established as the followers of the game，and then a distributed strategy update iterative algorithm is proposed，which realizes the stable convergence of the multi-UAV task allocation scheme and the optimization of the task revenue.Simulation results show that the proposed approach can effectively improve the efficiency of multi-UAV systems to complete multiple tasks at the same time，and can achieve efficient collaboration for the values of heterogeneous tasks in different environments.

Key words multi-UAV system;task allocation;Stackelberg game;iterative algorithm