基于EMD -樣本熵的軸流壓氣機喘振分析

黃澤浩，李良才，邵 勇，張 凡，胡肖肖

(中國艦船研究設計中心，湖北 武漢 430064)

0 引 言

軸流壓氣機設計體系對燃氣輪機的設計周期和性能有著重要影響[1]。目前常用的壓氣機喘振工況分析預測方法[2]可以歸納為3 類：三維數值方法[3]、試驗方法和經驗模型方法。其中，三維數值方法通過仿真等數值計算手段建立虛擬的物理模型，但是由于受到模型精度、計算方法和網格劃分數量等其他因素影響，所建立的物理模型只能在一定程度上反映壓氣機的內部工況，需針對具體情況具體分析，難以推廣使用。利用試驗方法[4]直接探究壓氣機喘振邊界是目前最準確最基本的方法。這種方法受限于成本、周期和環境因素的干擾難以實現。經驗模型方法[5 – 6]依賴于設計者工程經驗，利用現有的試驗數據和實測值多維輔助預判，是目前最為簡單有效的方法。此類方法需利用壓氣機運行時采集的傳感器信號，但是壓氣機運行時傳感器采集的一維信號并不能完全體現壓氣機多維、復雜的運行特點。因此，此時就需要將采集到的一維信號升高到高維上來體現其實際的運行狀態。經驗模態分解（EMD）是一種自適應的處理非線性、非平穩信號的方法[7]。EMD方法是基于復雜信號的局部特征時間尺度，把原始信號分解為有限個本征模態函數（IMF），每個IMF所包含的頻率成分不僅與采樣頻率有關，還會隨原始信號本身的變化而變化[8]。通過對一維信號的EMD分解可以把數據的維數進行一定的升高，但是高維數的數據不一定是原信號的本質信號，所以必須采用一定的降維方法把數據降到信號的本征維數上，此時的信號才可以從本質上代表原始信號[9]。而樣本熵作為近似熵的改進算法，其反映了信號的混亂相似程度，可以客觀反映故障與正常狀態的不同[10]。本文利用樣本熵對喘振和正常工況進行了識別，結果表明此方法可以有效地區分2種工況。

1 數據處理方法

1.1 經驗模態分解（EMD）

經驗模態分解（EMD）是由Huang等[11]在1998年提出的一種新的進行時頻分析方法。EMD分解通過平穩化處理時間序列，逐級分解原始輸入信號中不同尺度的波動或趨勢，從而得到一系列不同特征尺度的數據序列，這些序列稱為固有模態函數(intrinsic mode function，IMF)。IMF分量必須具備2個特征：一是其極點數和零點數相同(或最多相差一個)；二是其上下包絡線關于時間軸局部對稱。其具體的分解過程為：

步驟1求解輸入信號的所有局部極值點，再基于三次樣條曲線分別連接所有局部極大值和極小值點，最終形成上下包絡線，上下包絡線的平均值記為m1，求出：

如果h1滿足IMF的2個特征，那么其就是x(t)的第一個IMF分量。

步驟2如果h1不滿足IMF的2個特征，則把h1作為輸入信號，重復k次步驟1，得到h1(k?1)?m1k=h1k，使得h1k滿足IMF特征。記c1=h1k，將c1作為信號x(t)的第一個滿足IMF特征分量。

步驟3將c1從信號x(t)中分離出來得到：

將r1作為原始信號重復步驟1、步驟2，得到x(t)的第2個滿足IMF特征的分量c2，重復循環n次，得到信號x(t)的n個滿足IMF特征的分量r1,r2,r3···rn，當rn成為一個單調函數時，不能再從中提取滿足IMF特征的數據系列時，結束循環，得到信號x(t)的EMD分解。

rn代表了信號的趨勢，而cj中包含有不同頻率的成分并且是非等寬的。這一點正體現了EMD分解的自適應性。

1.2 樣本熵

樣本熵是由Richman[12]提出的一種新的時間序列復雜性測度方法，函數形式為SampEn(m,r,N)，其中數據長度為N，相似容限為r，維數為m及m+1。其具體的計算步驟如下：

設原始信號為x(1),x(2),x(3)···x(N)，共N個點。

步驟1將原始信號按順序排列組成m維矢量，即

步驟2定義X(i)與X(j)之間的距離d[X(i),X(j)]為兩者對應元素中差值最大的一個，即

步驟3給定閾值r，對每一個I統計d[X(i),X(j)]小于r的數目及此數目與距離總數N?m的比值，記作，即

則有：

再將維數加1，即對于m+1點矢量，得到Bmi+1(r)，即Bm+1(r)。

步驟4求解出該序列的樣本熵：

N為有限值時，則上式可以寫為

SampEn的值顯然與m，r的取值有關。由文獻[8]可以得知，m=1或2，r=0.1SD0.25SD（SD為原始數據的標準差）計算得到的樣本熵具有合理的統計特性。因此，本文選取r=0.2SD，m=2。

1.3 數據降維

實際上壓氣機的運行是一個多維的運行狀態，有很多因素對它的運行狀態產生影響。通過傳感器測量的一維時間序列可以理解為壓氣機高維復雜的空間運動向一維空間的投影。然而壓氣機運行狀態的本質維數并不一定是一維的，所以在投影的過程中，會受到很多其他因素的影響造成原本能夠表征壓氣機運行狀態的一些本質特征在向一維投影的時候發生變化、被削弱甚至消失，即微弱故障難以提取。這一現象導致在分析所測得的一維數據時很有可能造成特征提取錯誤、特征難提取等問題。因此，首先對采集到的信號進行EMD分解，使得信號的維數升高，然而一維數據升高到高維并不一定可以表征壓氣機實際運行的本質，并且還會有維數災難的出現，不利于分析。因此，通過對壓氣機本征維數進行估計，對EMD分解后的高維數據進行降維，使其降到本征維數從而可以反映出壓氣機的本質運行狀態。對高維數據降維處理是提取復雜多成分原始信號特征值，去除噪聲最常用的手段，具體優勢體現在以下方面[13]：

1）對原始數據進行有效壓縮以節省存儲空間；

2）可以消除原始數據中存在的噪聲；

3）有利于提取原始信號中的特征值，為后續的分類或識別提供基礎；

4）將高維信號投影到二維或三維空間，有利于信號可視化處理。

本文采用線性降維的主成份分析（PCA）的方法進行降維。

2 試驗裝置

本試驗壓氣機為三級軸流壓氣機，在一級、二級之間以及三級處各安裝有一個高頻動態壓力傳感器，用于實時采集三級軸流壓氣機動態壓力信號的變化。設置排氣節流閥的開口流量模擬實際壓氣機的運行環境，將采集的數據存儲在計算機上。

3 數據處理

通過調節排氣節流閥的開度改變壓氣機的工況，發現當排氣閥的開度調節到20°時，壓氣機在9 600 r/min時出現喘振，因此對喘振前后的級間壓力、三級出口處的壓力信號進行處理。由于在采集的過程中信號會受到電氣干擾，在處理之前首先采用拉伊達準則對原始信號進行處理消除電器干擾的影響。圖1為9 600 r/min時喘振前后級間壓力原始信號以及經過拉依達準則處理后的信號。

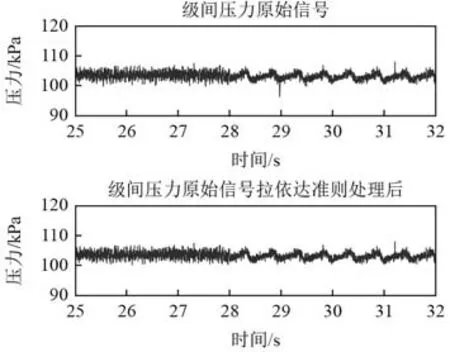
圖1 20°，9600 r/min喘振前后級間壓力信號及拉依達準則處理后的信號Fig.1 Interstage pressure signals before and after surge of 20° ，9600 r/min and signals processed by the Rajida criterion

對處理后的信號進行EMD分解，其前8個IMF如圖2所示。

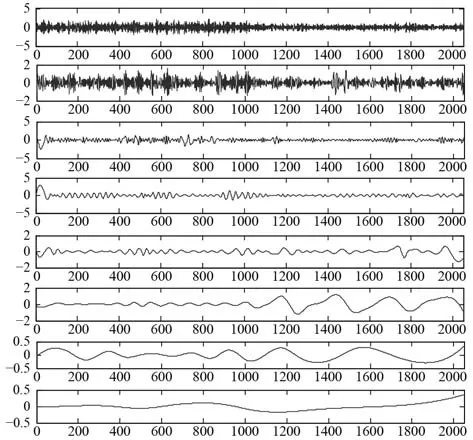
圖2 EMD分解的前8個IMF分量Fig.2 The first 8 IMF components of the EMD breakdown

可以看出，第6個IMF分量可以反映出壓氣機喘振時出現的波動。

因此，通過記錄的時刻得知在28 s時壓氣機發生了喘振，對級間壓力和三級出口壓力分別取發生喘振前2 s的數據以及發生喘振后2 s的數據。進行EMD分解，并且對分解的信號選擇主成份分析（PCA）方法進行數據降維，在對本征維數的估計基礎上把維數降到三維，計算各個的樣本熵。表1和表2列出了級間壓力以及三級出口壓力在喘振前后的樣本熵。樣本熵三維圖如圖3所示。

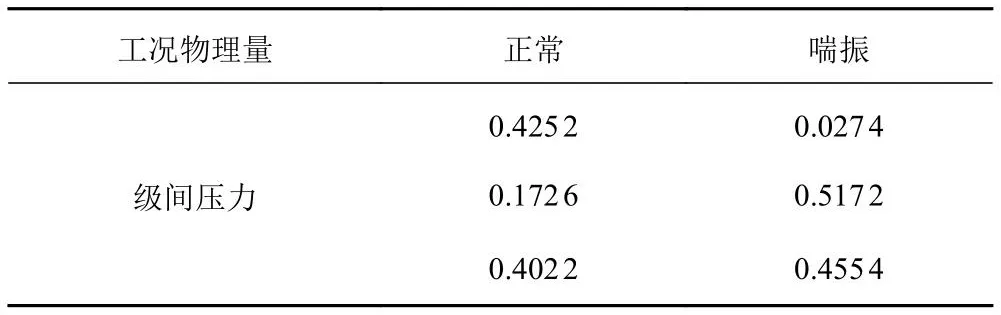
表1 級間壓力喘振前后樣本熵Tab.1 Sample entropy before and after interstage pressure surge

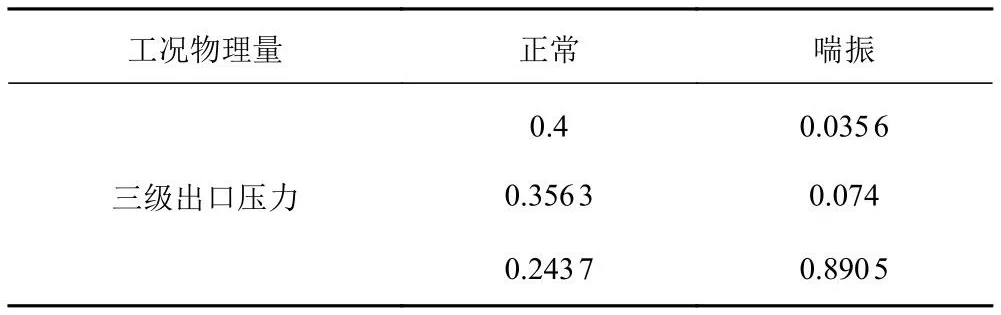
表2 三級出口壓力喘振前后樣本熵Tab.2 Sample entropy before and after the three-stage outlet pressure surge

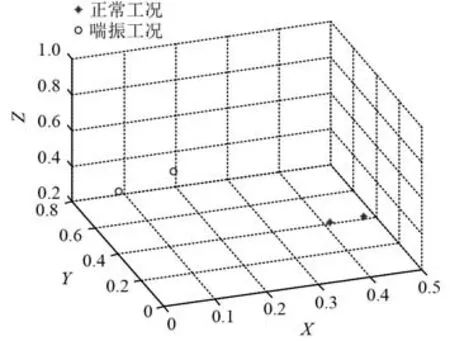
圖3 壓氣機正常與喘振工況樣本熵Fig.3 Sample entropy of compressor under normal and surge conditions

由計算結果可以得知，在三維圖中喘振工況和正常工況分別聚集在一起，具有良好的聚類效果，說明利用樣本熵的方法可以對2種工況進行區分，證明此方法可以對壓氣機的2種工況進行判斷，用于壓氣機喘振的實時監測。

4 結 語

通過EMD分解使得傳感器采集的一維信號可以在高維來體現壓氣機的實際運行狀態。但是在高維時并不是所有的維數都起作用，有的維數會相當于“噪聲”從而影響本質運行狀態的體現。因此，采用降維的方法把高維的數據降到可以表征壓氣機運行狀態的本質維數上，再通過樣本熵把壓氣機正常工況與喘振的工況區分開，為壓氣機的監測提供了一定的理論基礎。