如何利用十字相乘法分解因式

陳愛榮

所謂的“十字相乘法”就是借助畫十字交叉線分解系數，從而把二次三項式ax2+bx+c分解因式的方法.十字相乘法在因式分解中經常用到，它可以解答很多公式法、配方法等不能解答的問題.在運用十字相乘法分解因式時需要拆分常數項或二次項系數，并逐一核驗對角線乘積的和是否等于一次項系數，若相等，則拆分成功，否則拆分不成功，需要舍棄，最后將拆分后的項按照乘積的形式書寫出來，即可完成因式分解.

一、二次項系數為“1”時，拆常數項，湊一次項

例1分解因式y2-8y+15.

分析：此二項式的二次項系數為“1”，直接拆分常數項15即可.常數項15=1×15=-1×（-15）=3×5=-3×（-5），如圖2所示，經過多次嘗試核驗，發現只有第4種情況滿足條件.

分析：此題可直接拆分常數項-15，因為常數項是負數，所以拆分的因數中需要安排一個負號，這就需要核驗一次項系數后確定.-15=-1×15=1×（-15）=-3×5=3×（-5），-1 15和1×（-15）的情形很容易看出不符合要求，另外兩種情形如圖3、圖4所示；拆分為圖3核驗結果為1×5+1×（-3）=2，不等于一次項系數-2，舍棄；圖4驗核結果為1×（-5）+1 3=-2，等于一次項系數-2，核驗正確.

評注：從以上的解題過程可以發現：當常數項為正數時，把它分解為兩個同號因數的積，每個因數的符號與一次項系數的符號相同；當常數項為負數時，把它分解為兩個異號因數的積，其中絕對值較大的因數的符號與一次項系數的符號相同.

二、二次項系數不為“1”時，拆兩頭，湊中間

例3分解因式5x2+7x-6 .

分析：此題中二次項系數不為“1”，需要拆分二次項系數和常數項系數，即5=1×5，-6=-1×6=1×（-6）=-2×3=2×（-3），如下圖6-1至6-8所示，然后逐一核對對角線乘積和與一次項系數是否一致，由表1可知，圖6-6的分解符合題意.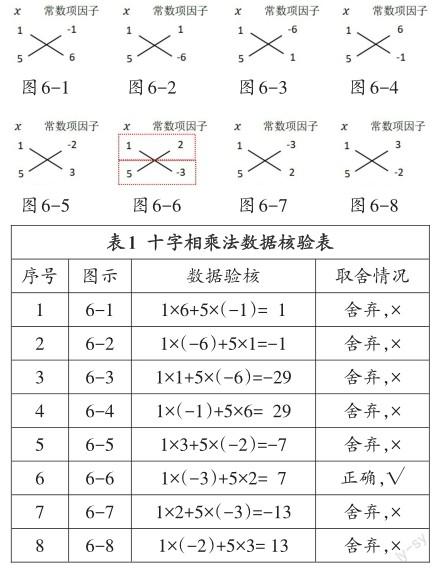

解：5x2+7x-6=（5x-3）（x+2） .

例4分解因式9+5x-4x2.

分析：此題二次項系數為負數，如果提取負號則可以轉化為二次項系數為正數的情形，即9+5x-4x2=-（4x2-5x-9）.然后求解出4x2-5x-9的因式分解結果即可.二次項系數可拆分為4=1×4=2×2，常數項可拆分為-9=-1×9=1×（-9）=-3×3，如下圖7-1至7-9所示，然后逐一核對對角線乘積和轉化后的一次項系數（-5）是否一致.由表2可知，圖7-2的分解符合題意.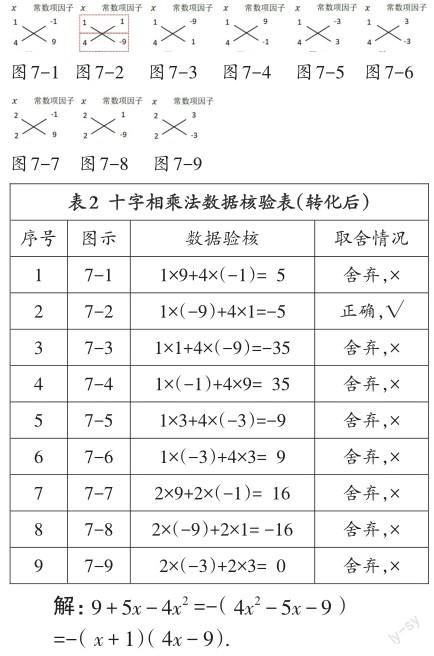

評注：當二次項系數和常數項系數有多種拆分情況時，同學們需要逐一核驗拆分后對角線乘積的和是否與一次項系數一致，然后舍棄所有不符合的情況，保留正確的拆分情況.此外，如果二次項系數是負數，則應先將負號提到括號外面，使二次項系數為正數，然后再進行因式分解.