大自然的實與虛

彭鵬 劉博聞 高策

從牛頓時代起，物理學家開始使用數學來描述世界。在經典物理學中，實數可以完整描述所有經典物理量，虛數僅僅是為了計算方便而引入的計算工具。在薛定諤、海森堡等量子力學先驅建立量子力學的過程中，虛數以第一原理的形式被引入理論。但它在量子力學中仍是抽象的概念，物理學家并沒有賦予其任何實際的物理意義。因為，通過實數概率值的形式可以完成對量子力學實驗的描述，并不需要虛數。然而，物理學的目標是通過理論來解釋實驗現象，而非描述實驗現象。鑒于上述原因，物理學家對在量子力學中使用虛數是極其忐忑和糾結的。

為了消除顧慮，一些物理學家試圖去除量子力學理論中的虛數，完全依靠實數來建立量子力學的理論體系。但是這樣的實數量子理論能夠完整地描述量子世界嗎？如當年玻爾和愛因斯坦對量子力學是否具有完備性的爭論一樣，這個問題同樣令人惴惴不安。

就像貝爾不等式檢驗實驗反駁了隱變量理論那樣[1]，2022年，中國科學技術大學的潘建偉團隊和南方科技大學范靖云團隊，分別獨立通過一個類似貝爾不等式檢驗實驗的實虛檢驗實驗證明，虛數對標準量子力學理論來說是必不可少的，并且扮演著關鍵的核心角色。

虛數的建立和初步應用

虛數的來源是負數的平方根。意大利數學家卡爾達諾（G. Cardano）在其1545年出版的《偉大的藝術》中提到了一個問題，能否把10分成兩部分，使它們的乘積為40？這個問題實際上就是求解一個一元二次方程，但是其判別式Δ<0，結果中會出現負數的平方根，即沒有實數解。若沒有虛數，此方程無解。在求解一元二次方程時，負數開根號并不影響計算過程；但在解一元三次方程時則會出現問題，當Δ<0時，方程會有三個不等的實數根，按照求根公式求解，就會遇到負數開根號。1572年，意大利數學家邦貝利（R. Bombelli）在《代數學》中，第一次大膽利用虛數運算規則解出了方程的三個實數解。數學家由此認識到虛數的重要性。1637年，笛卡爾在《幾何學》中，首次將負數的平方根稱為imaginary number（虛數），意思是虛構的、不存在的數。萊布尼茲直接稱虛數為“介于存在和不存在之間的兩棲物”。正如解一元三次方程那樣，使用虛數能非常方便地獲得最終的實數解。因此，它最初只是作為工具引入數學計算，沒有實際意義。

此后，高斯、柯西、歐拉、傅里葉等數學大家均對虛數進行了大量深入的研究。1748年，歐拉在《無窮小分析引論》中，提出了歐拉公式eix=cosx+isinx，將三角函數與帶有虛數的指數函數關聯起來，簡化了三角函數的計算，并將三角函數的周期性引入指數函數。不過，他對虛數的態度仍不置可否，認為：“它們（虛數）既不是什么都不是，也不比什么都不是多些什么，更不比什么都不是少些什么。它們純屬虛幻。”1777年，歐拉最早引入虛單位i。1807年，傅里葉首次提出“任何周期信號都可用正弦函數級數表示”。1822年，數學應用于物理學的里程碑式著作《熱的分析理論》出版，該書首次描述了傅里葉變換：通過對函數乘以一個帶有虛數的指數，就可以實現函數在時域和頻域之間的轉換。有了虛數便有了復數的概念，1832年，高斯引入復數的概念并給出幾何解釋，將復數與復平面一一對應起來。實數是一維數，只有實數軸上移動的自由度。復數的形式為a+bi，其中a為復數的實部，b為復數的虛部，相當于增加了額外的一個自由度。實數域拓展到復數域，移動自由度由一條線變成了由實數軸和垂直于實數軸的虛數軸構成的二維復平面。

隨著虛數不斷得到應用，學術界逐漸接受了虛數的概念，同時也為它進入物理學領域打下基礎。由于復數可以方便而簡潔地描述物理量的周期、相位、振幅等信息，其在物理學以及工程領域得到了極其廣泛的應用。比如，在處理交變電路時，可以將電壓、電流、阻抗等物理量表示為復數形式，然后按照復數的運算規則進行運算，最后取實部或虛部就可得到最終的實數結果；傅里葉變換的一個重要應用就是信號處理，類似化學中分析物質成分一樣，它有助于處理分解信號，從而確定信號的成分。費曼將歐拉公式稱為“我們的珍寶”“數學中最非凡的公式”，肯定虛數對物理學發展的重要性。法國數學家阿達馬（J. S. Hadamard）曾說：“在實數域，連接兩個真理的最短路徑是通過復數域。”

量子力學中的虛數

楊振寧曾提到，“20世紀理論物理學的三個主旋律是：量子化、對稱性和相位因子”，可以說，這三個主旋律的基本架構都離不開虛數。

那么，虛數到底有怎樣的物理意義？可以從復數在方程所蘊含的信息窺探一二。復數包含波函數的振幅和相位信息，二者是量子力學最為核心的關鍵因素。薛定諤雖然建立了波函數，但并沒有參透其真正內涵。波函數所描述的波與常識中的波完全是兩回事，前者并非真實三維空間的函數，而是希爾伯特空間的函數，希爾伯特空間最早由馮·諾依曼引入量子力學，是構造空間中的一個復值空間。玻恩將區別于經典物理學的非決定性引入量子力學，賦予波函數極其特別的概率解釋。波函數的振幅信息決定了粒子某一時刻在某一位置出現的概率，而相位（差）信息則是量子相干性的來源。量子相干性是量子世界區別于經典世界的關鍵特征，它的存在會促使量子行為向經典行為轉變。量子退相干行為是量子計算在實現過程中亟需突破的一個挑戰，量子干涉測量則提供了一種更為精密的測量方式。

規范理論中的虛數

物理學中大多數方程都涉及某種對稱性，而對稱性是規范理論的核心。規范的本意是標尺或者標度，用以定義標準。生活中最常見的規范對稱的例子是電壓。對電路產生影響的是電壓差的大小，而不是電壓絕對的大小。電路整體電壓同步增加，不會影響電壓差的大小，因而不會對電路產生影響，這是一種規范不變性。虛數在規范變換中同樣發揮了舉足輕重的作用。

1905年，法國數學家龐加萊發現，洛倫茲變換可以看作是在由時間的虛坐標ict（c為光速）和歐幾里得空間三個實坐標構成的四維時空中的坐標旋轉變換。隨后，德國數學家閔可夫斯基（H. Minkowski）基于龐加萊的工作，在構建的四維時空中對麥克斯韋方程組和愛因斯坦的狹義相對論進行了進一步研究，更為簡潔地闡釋了二者的洛倫茲不變性。洛倫茲不變性是狹義相對論的基本性質，反映了兩個作相對勻速運動的慣性參考系之間坐標變換的不變性。ict賦予了時間軸以長度的量綱，時間尺度就等同于是一個虛的空間尺度，“在這種情況下，滿足（狹義）相對論要求的自然定律取這樣的數學形式，其中時間坐標的作用與三個空間坐標的作用完全一樣。在形式上，這四個坐標就與歐幾里得幾何學中三個空間坐標完全相當”，將過去認為是相互獨立的時間和空間用四維時空統一起來。進一步，1915年，愛因斯坦在普魯士科學院的發言中，正式提出廣義相對論，將引力描述為時空的幾何屬性——曲率；提出引力的場方程，將物質的能量、動量與時空曲率聯系到一起，開創了物理的幾何化。

1918年，德國數學家外爾（H. Weyl）受愛因斯坦廣義相對論的影響，在《空間，時間，物質》一書中開始嘗試統一四大力中的引力和電磁力，并最早引入規范的概念。為了將引力理論的幾何化推廣到電磁理論，外爾發展了一種新電磁學的幾何解釋理論。他的做法是引入一個標度因子λ（x）=eθ（x），這樣的數學結構展現了一種新的對稱性，即規范不變性。從數學的角度看，外爾的理論如此優雅和美麗，他在文章中明確表示：“我有足夠的勇氣相信，所有的物理現象都可能源于一個普遍的定律，即數學上最簡單的定律。”同時，他在給愛因斯坦的信中聲稱：“我相信，在這些日子里，我成功地從同一個來源得到了電和引力。”

然而，外爾的理論失了物理的真。在廣義相對論中，愛因斯坦始終用完全相同的時鐘和尺子，即相同的標準，而外爾的做法卻使得“標準”可以隨意改變，這在物理學中是不被接受的。因此，當愛因斯坦看到外爾的理論時，立即提出反對意見：“這是一項一流的天才之舉。然而，到目前為止，我還是無法消除我對標度的反對意見。”同時，他提出一個假想實驗：兩個時鐘從同一地點出發，分別沿著兩條不同路徑移動，最后再回到出發點。如果外爾的理論正確，時鐘在移動的過程中，標度會不斷連續變化，不同的移動歷史會造成兩個時鐘的快慢不一樣，即時鐘的快慢會依賴于移動的歷史。愛因斯坦最后表示：“遺憾的是，這個理論的基本假設對我來說似乎是不可接受的。”盡管外爾的理論并不成功，但其規范不變性的思想在統一場論的發展中扮演了重要的角色，標志著現代規范理論的誕生。

虛數在量子力學理論中的應用，為解決標度變化問題提供了新思路。1922年，薛定諤猜想，在外爾的變換中可以引入虛數。1927年，蘇聯物理學家福克（V. Fock）和德國物理學家倫敦（F. London）分別獨立從量子力學的角度對帶電粒子與電磁場的相互作用進行研究，對外爾的理論加以改進，將實數形式標度因子嵌入虛單位-i，從而將尺度變換更改為相位變換。如此這般，就能打消愛因斯坦的質疑了，時鐘路徑的不同只會影響時鐘相位的變化，卻并不會影響時鐘的快慢。正如倫敦在《外爾理論的量子力學解釋》中所描述的那樣，“這意味著任何空間間隔都必須被看作是一個復數量，而整體間隔測量的外爾變量的結果是在常數模相位的變化”。雖然很難理解虛數的物理意義，但對于虛數的使用，倫敦是堅定的：“一個更為嚴重的問題是如何理解路徑連接的復數形式。我們不應該始終將自己限制在實數領域。而是應該注意到另一個事實，那就是波函數本質上就是復數的。”不過，他同時也感到不安：“正是這種波（復振幅）經歷了外爾為他的規范尺度所假定的影響，作為當時物理學的一個多余元素，不得不賦予它一種形而上學的存在。”在當時看來，虛數始終是實驗上一個不可測量量。

物理學家把具有相位的復振幅引入大自然的描述，這不僅成為量子力學的基本核心內容，同時還揭開了建立標準模型的序幕。狄拉克曾這樣描述相位對于建立量子力學的重要性：“相位這個物理量巧妙地隱藏在大自然中，正由于它隱藏得如此巧妙，人們才沒能更早建立量子力學。”更進一步闡述，所有的相互作用包括電磁力、強力、弱力、引力等都是某種形式的規范場，而規范場論中的對稱性、規范變換等核心概念無不與相位相關；同時，規范場與數學概念纖維叢關系密切，而纖維同樣是復相位。可以說，將相位放置到任何高的位置都不為過，正如楊振寧描述相位：“規范場就是把相位這個觀念的重要性提到最高，等于是問這樣的問題：為什么有電磁波？為什么有引力？為什么有強力？為什么有弱力？這些，都是因為相位的對稱的觀念而來的。”他認為，如果現在重新命名，規范不變性應該叫相位不變性，而規范場應該稱為相位場。

尋找實數量子理論

虛數在數學中是必不可少的，并且為現代物理學的發展立下汗馬功勞，但是它一直以來始終是一個在實驗上形而上學的不可測量量。在量子力學中，雖然算符是虛數的形式，但可觀察量的算符一定是厄米算符，因為厄米算符的本征值為實數，任何可觀測量都是實數。這是量子力學建立的五個基本假設之一。由于虛數無法用實驗進行測量，那么就產生一個疑問：是否可以用純實數來建立量子力學？

不過，2009年轉機出現。加拿大滑鐵盧大學的莫斯卡（M. Mosca）團隊在理論上證明，可以完全脫離虛數，僅使用具有實系數的狀態和算符，通過實數形式的希爾伯特空間描述量子力學系統及其演化，包括連續時間演化和多粒子體系的演化，能重現標準貝爾定理所預測的統計實驗結果。該理論提供了對虛數質疑的依據，但依然缺乏一個真正的實踐檢驗。

實驗驗證

2021年，巴塞羅那科技學院的雷諾（M. Renou）等人為解決虛數和實數之爭，提出了一個在當前技術條件下切實可行的實驗方案[2]——實虛檢驗實驗。該實驗方案對貝爾不等式檢驗實驗進行了擴展，將一個糾纏源和三處測量點改為兩個糾纏源以及三處測量點。研究人員在理論層面分析發現，標準量子力學以及實數量子力學的實驗結果不同。若實虛檢驗實驗成功付諸實踐，就可以駁斥實數量子力學。

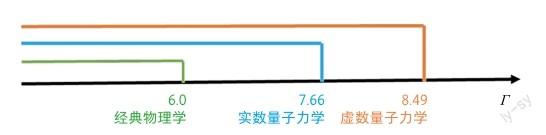
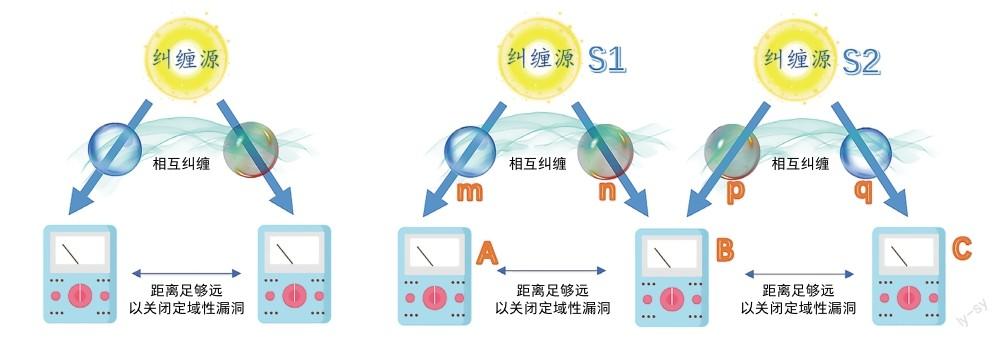
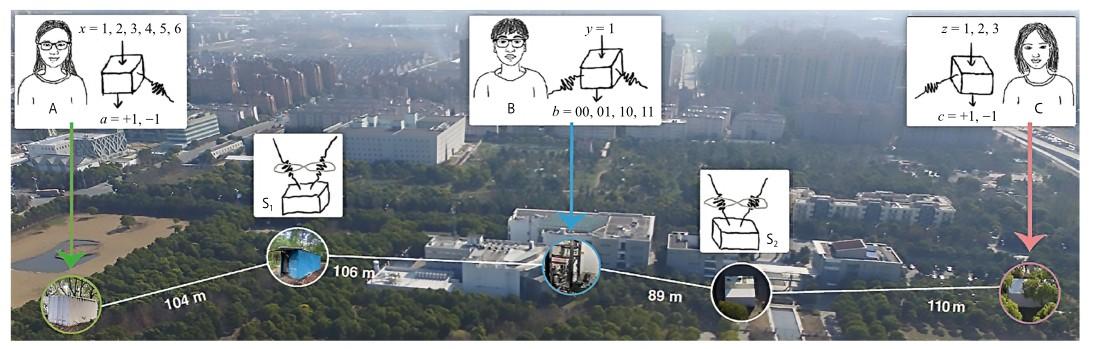
貝爾不等式檢驗實驗中，僅需要多組相互糾纏的粒子分別發射到相距足夠遠的兩處進行統計測量，就可以獲得實驗結果。實虛檢驗實驗則需要兩個獨立的糾纏源分別發送兩組糾纏粒子對到三處測量點。糾纏源S1和S2分別制備糾纏粒子m、n和p、q，n、p發射到B測量點，m、q分別發送到A、C測量點，對B處的n、p兩粒子進行一次特殊的測量，就可以實現本來毫無關聯的m、q兩粒子的糾纏，這個過程被稱作糾纏交換[1]。將上述過程重復多次，并加權各處聯合測量的概率分布，可獲得關聯參數。理論分析虛數量子力學關聯參數上限值Γ為6≈8.49，而實數量子力學為7.66，經典物理學則為6.0。如果實驗測量獲得的關聯參數值在7.66和8.49之間，就可以排除實數量子力學。

得益于量子調控技術的快速發展以及大量貝爾不等式檢驗實驗的經驗積累，潘建偉團隊和范靖云團隊分別利用超導量子比特和和光子的偏振態完成了實虛檢驗實驗驗證，獲得的實驗結果均大于實數量子力學的上限值而小于虛數量子力學的上限值，有力地駁斥了實數量子力學。這兩個實驗在某種程度上表明虛數在量子力學中發揮著非常基礎性的作用，而這是實數無法替代的。不過就像貝爾不等式檢驗實驗一樣，上述實驗也存在漏洞[1]，隨后還會有更多更趨于完美的實驗。

除了上述實驗，還有一項實驗也充分證明了虛數不虛。2011年，加拿大國家計量標準研究所的倫迪恩（J. S. Lundeen）團隊第一次在實驗上實現對波函數實分量和虛分量的直接測量[3]。這項實驗并不是通過傳統層析方法去間接獲取波函數的信息，而是直接將波函數的實部和虛部數值呈現在測量裝置上。基于不確定性原理，一旦精確測量粒子的位置信息，就無法再精確測量其動量信息，這種不確定性由帶有虛數的對易關系來描述。一般認為，測量過程被看作是儀器與被測物理系統之間的耦合，會導致儀器指針的偏轉，破壞物理系統的原始狀態，從而影響其他狀態的測量。隨著技術的發展，被稱作“弱測量”的實驗技術誕生，它可以最大限度降低測量過程對于量子態的干擾，不會影響其他狀態的測量：先對位置進行一次“弱測量”，隨后再對動量進行一次標準的測量，進而直接測量了單個光子復波函數。隨后，物理學家進一步直接測量了更加復雜多粒子體系乃至糾纏量子態的波函數。這樣，量子態測量就有了簡單而直接的定義：對一個變量進行弱測量，然后對不對易變量進行標準測量，最終得到兩次測量的平均結果。目前，所有的實驗均表明虛數量子力學始終是描繪自然界最為成功的理論。

相對論和量子力學是當代物理學大廈的基石，它們的核心內容如波函數、不確定原理、規范變換、場方程、量子糾纏、量子干涉乃至相對論性的波函數方程——狄拉克方程等，均離不開虛數的使用。從上文可知，盡管虛數在這些理論中起到最為基礎的作用，卻沒有明確的定義，而是以一種抽象元素的形式被引入。因此，如何用虛數解釋奇妙的量子世界，或者虛數蘊含怎樣深刻的物理內涵，還需要進一步去探究。

[本文相關研究受國家自然科學基金青年科學基金項目（11904217）、國家社會科學基金重大項目（16ZDA113）、山西省科技戰略研究專項（202204031401039）資助。]

[1]彭鵬， 劉博聞. 貝爾檢驗簡史. 科學. 2023， 75（1）： 36-41.

[2]Renou M O， et al. Quantum theory based on real numbers can be experimentally falsified. Nature， 2021， 600（7890）： 625-629.

[3]Lundeen J S， Sutherland B， Patel A， et al. Direct measurement of the quantum wavefunction， Nature， 2011， 474（7350）： 188-191.

關鍵詞：虛數 糾纏交換 貝爾實驗 量子力學 實虛檢驗實驗 ■