高中物理解題方法和技巧

胡金鳳

【摘要】高中物理在高中學生中的地位是毋庸置疑的，學習物理既能提升學生的知識素養，又能改善他們的整體素質.因為物理學的重要性，所以教師在課堂上讓學生進行物理訓練，讓學生了解一般的物理定律，從而提高學生的運用能力.本文就如何提高高中物理問題的解題水平，給出相應的教學對策.僅供參考.

【關鍵詞】高中物理；解題方法；教學方法

隨著經濟不斷發展，教育發展日益受到重視.但是對于物理來說，它的答案是唯一性的、固定性的，這使學生產生了極大的困擾，究其根本，在于沒有任何的技術與方法來解答這個問題.從歸納學生的習慣，引導學生解題的誤區入手，探討解題的技巧和途徑［1］.

1 高中物理及題型發展現狀

1.1 物理科目發展現狀

結合高中課程的發展與變革進行分析，物理這門學科從某些方面來說并沒有太大改變.但是在考試方面進行了改變，通常，物理問題的解決方法也會有所變化.現在，隨著新的高考改革，選擇物理的學生已經不多了.從數據上看，就算是那些成績比較好的學生，在物理上也是處于下風的.原因很簡單，學生不懂物理的奧妙，也不懂解題的方法，物理學的知識體系亟待改革，而這一變革，就是從根本上改變［2］.

1.2 物理解題內部分析

就物理解題來說，12個常見的題目，都是針對不同的問題進行的.有了這些知識，他們就能更好地解決物理問題.而對那些成績相對較差的學生來說，簡單的問題往往會成為一道難題，導致了現在的物理題出現了兩極化現象.中學的物理不是表面的，而是有了很多定義，有了很多概念要背，而物理公式越來越豐富.解題方法又不僅限于數種，題型變換還讓很多學生感到頭痛，為此要想辦法解決［3］.

2 解題技巧方法探究

2.1 加強課堂練習

在課堂上，物理教師要在學生完成有關的知識后，加強課堂的基本功訓練，安排習題，以鞏固本課程的學習.習題時，教師還要在原來的題目基礎上進行擴展，仔細設問，激發學生的深層思考，發現知識點之間的聯系［4］.

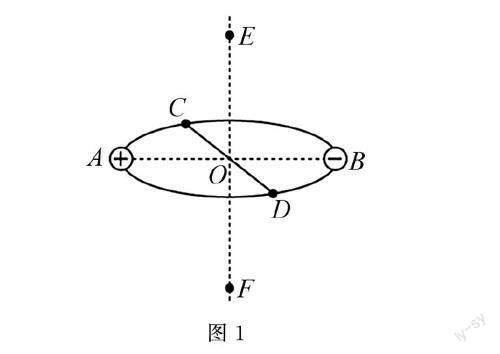
例如 如圖1所示，A、B、C、D為圓周上的四個點，AB和CD線交圓心O，并互相垂直，E、F是關于O點對稱的兩點，但與O點的距離大于圓的半徑，E、F兩點的連線與AB、CD都垂直.假定把一個帶+ Q的點電荷放在A點，把一個帶-Q的點電荷放在B點上，那么以下的表述正確的是（? ）

（A）O點和E點之間的電勢差遠遠大于O點和C點之間的電勢差.

（B）D點和E點電勢相同.

（C）沿C和D連線從C至D運動一正點電荷，所受的電場強度先降低后增加.

（D）把一個負電荷從C點向F點運動，軌跡為沿半徑移動到O點后再沿直線移動到F點，在此點上電荷的勢能先是增加，然后又降低.

答案：（B）.

解析 CD和 EF所處的平面是一個等勢平面，電荷在等位面上運動，電場力不作任何功，因此（A）和（D）是錯的，（B）是對的；從點電荷場強度的計算公式出發，結合電場的疊加原理，給出了一種計算方法，當C和D連線中C至D電場強度先升后降時，沿著C和D連線從C至D運動一個正點電荷，電荷所受電場力先升后降，（C）是錯誤的.

除了基礎試題的演練，學生還應該在教師的指導下鞏固自己的基礎.

例如 以“電場能的性質”為例，從重力勢能的特性出發，討論了它和電勢的相似性.在探討和探討電位能時，請參閱以下問題：（1）在同樣位置的正電荷與等負電荷的電勢能是一樣的嗎？（2）可以用什么方式來比較電勢能的大小？（3）怎樣定義電勢？怎樣比較電勢？在學習的過程中，將電位與重力位的比較、電位與場強的比較，使學生能夠從點到面的記憶書本，逐漸地將所學的知識連接起來，形成一個完整的網絡.在教學中，學生要在教師的指導下，繪制出相應的思維導圖，找出電場、電勢、電場力之間的聯系，從而將所學知識重新整合、重新整理，挖掘知識點與知識點的內在關系，通過橫向、縱向的關聯，使知識結構得到優化，從而形成物理學科的知識體系.

2.2 找到解題突破口

學生在解答問題時，必須具備良好的判斷能力.讓學生對題目的含義有更深入的了解，避免出現“回答不了的問題”.此時，中學物理教師要對學生進行考題能力的培養.教師可以根據學員的練習成果，進行小組交流，探討解題的方法.學生也逐漸了解到，在做題目的過程中，要把已知的、不確定的都列出來，并把它們聯系起來.在此基礎上，學生能夠發掘出物理知識，并找到相應的解決辦法［6］.

例如 當電流在相同有效時間內經過兩個電阻絲甲與乙時，甲所產生的熱大于乙所產生的熱，則以下說法正確的是（? ）

（A）乙的電阻必然小于甲的電阻.

（B）乙兩端的電壓必然小于甲兩端的電壓.

（C）乙的電流必然小于甲的電流.

（D）乙的功率必然小于甲的功率.

有些學生回答這個問題時，對于物理這一概念，人們很容易產生混淆，也許想的是：電阻，電壓、電功率與電流之間的規律及其有關關系等.做題時，有部分學生因為不能真正把握好該部分知識點，致使其在做題時也含糊其辭，因此，有一種追隨感覺，感覺哪個對選哪一個.有些學生物理基礎稍好，就把4個答案逐組輸入習題，一一核實回答是否正確.這類辦法可以說是個好辦法，尤以判斷題為甚.但題型一變化，出來就是應用題與填空題了，然后，學生無法套用結論了.所以，在做作業時，要引導學生正確對待問題的態度，同時要培養在日常生活中尋找突破思維的習慣.

為了讓學生更好地理解這個問題，我讓學生把自己所學到的東西聯系起來，找到“電阻絲”“熱量”之類的常用詞匯，從大量的物理常識中挑選出來，最后，有人說出了“焦耳定律”.讓學生在學習焦耳定律時，并且要他們說出這個規律和哪些因素相關，該規律有哪些解題方式.再請學生談談這個習題到底有哪些解答.再通過學生的持續溫習，持續推理，他們最終會明白，這道習題答案就是選項（D）.

2.3 注意審題的認真性與要點分析

學生審題時，應沉下心來，避免焦慮焦躁情緒.要注意解題過程，把握物理過程的特征，可以劃分為：步驟解題：在完成題目后，要把與題目有關的各個環節進行合理的分解，分成若干個步驟，便于分解.通過對物理過程和選擇的綜合分析，得出問題的解決辦法.聯系發展法－面對所有關系的物理現象，我們都應弄清楚步驟間的具體聯系，進而利用研究所用的物理量，在它們的連接點上尋找解決的方法.在每個問題的求解中，要根據每個問題的基本物理原理和應用方法，適時地尋找出適合自己的最佳方案和解題方案，更具體地講，學生就要將所有的方法和重點都運用到最大限度，便熟能生巧.

2.4 培養學生的逆向思維

逆向思維就是一種求異思維，是一種用相對觀點來分析已成定論的東西或思想觀念.

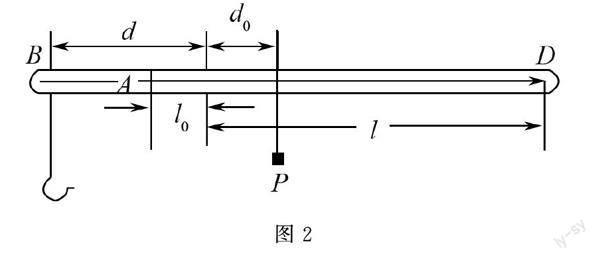
例如 有一個精確的桿秤，現在只給一個帶刻度的直尺，需要用來測量這個桿秤秤砣的重量，請推導出一個表示秤砣重量的公式來解釋需要測量的數量.

分析 這道題對獨立思維能力考查要求極高，因為題目沒有更多的條件，所以在解題時，學生往往會有一種不知所措的感覺.分析這個問題，首先要做的是一個小的試驗，在這個試驗中，我們已經知道了它的重量，要用試驗方法找到它的每一個標尺的位置和零點.然后，運用反向思維，考慮在知道了標尺的條件下，如何確定秤砣的重量.題中已經明確給出了秤桿上各刻度的數值，屬于隱含已知量，因此可得秤桿結構見圖3.

2.5 高效應用互聯網信息技術

在計算機網絡技術高速發展的今天，各種現代教育方法和技術不斷更新，教師可利用互聯網信息技術來設計具體課程，從而達到良好效果.在中學物理課程中，教師要合理地利用網絡信息技術創造更全面和多樣化的教學策略與課程.教學中，教師可以利用網絡手段進行上網，利用搜索引擎查詢各種教學資料、教育資源等，將教材中各種實用知識點集成一起，引入課堂.教師還可以通過網絡下載教學視頻和教學課件，將教學視頻和教學課件中的具體信息進行綜合，從而為教師的教學提供了更為靈活的教學方法.

2.6 懂得運用邏輯思維能力

當我們遇到與高中物理有關的問題時，我們會按照教師的講解，學會用自己的邏輯來解決問題.在解題前，我們必須要把物理和機械的基本知識都掌握到一定程度，這樣在解題的時候，我們可以將力學的知識分解開來，讓解題的步驟變得更容易.

例如 在物理力學問題中，存在著兩種互相糾纏的問題，我們可以把它們看成一個整體，用這種方法來解決問題，而且學習起來也比較容易.在解決物理和機械問題時，我們必須具備類推的能力，因為力學與其他物理問題的解法具有共通性，所以要學會如何求解這些問題.

2.7 做到全方面掌握，逐漸提高綜合能力

對于高中階段的學生來說，要學習好物理力學，首先要把基本的知識做一個系統的歸納，然后才能全面地掌握.我們不能忽視基礎知識，也不能浪費時間去思考，想要從根本上解決問題，就必須一步一個腳印地學習，正確地理解力學的原理，才能提高解題的水平.為避免問題發生，我們要注意掌握一些比較簡單的物理定律和知識，

例如 牛頓運動定律，引力定律，能量守恒定律，動能定律，動量定律，動量定律，動量定律.只有在對其基本概念、基本理論、基本法則完全了解后，才能更好地尋找出解決問題的思路和途徑.另外，因為物理與數學有許多交集，物理中到處都是數學，而物理又是無時無刻不在體現著數學，因此要想把物理力學的知識掌握得更好，就必須要有足夠的數學基礎.所以，在中學階段，我們需要學習如何運用數學工具來解決物理問題.

3 結語

就中學物理的問題，在解決問題上，仍然存在著很大的爭論.不同的學校還制定了各種不同的教學計劃.每個人都有自己的特長，不能讓所有人都用一種方式來解決問題，這要從不同的角度出發，要根據不同的學生的不同，因人而異，如果因材施教的話，在教室里就不能快速掌握解題的知識.作為學習的主體，要讓他們在教師的協助下，更多地關注自己的學習，讓他們能夠發現自己的知識和解決問題的方法，從而使得高中階段的整體學習變得容易.

參考文獻：

［1］張秀英，湯國平.掌握物理規律優化高中物理解題思路［J］.數理化解題研究，2020（13）：60-61.

［2］李忠斌.微元法在高中物理解題中的應用解析［J］.新課程，2020（7）：145.

［3］夏光輝.等效思維在高中物理解題中的應用［J］.數理化解題研究，2020（25）：97-98.

［4］許奇龍.極限思維法在高中物理解題中的有效應用［J］.數理化解題研究，2020（34）：75-76.

［5］張昌鈺.基于等效思維的高中物理解題研究［J］.文淵（高中版），2020（7）：179.

［6］何維鵬.高中物理解題思路障礙及對策討論［J］.中學生數理化（學習研究），2020（6）：39.